第2章 四边形 单元检测基础卷(含解析)
文档属性
| 名称 | 第2章 四边形 单元检测基础卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 535.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-28 09:47:45 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第2章四边形单元检测基础卷
班级__________姓名____________总分___________
一.选择题(共12小题,每题4分,共48分)
1.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
2.若一个多边形共有9条对角线,则它是( )边形.
A.五 B.六 C.七 D.八
3.一个四边形,截一刀后得到新多边形的内角和将( )
A.增加180° B.减少180°
C.不变 D.以上三种情况都有可能
4.在下列正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
5.如图,在平行四边形ABCD中,都不一定 成立的是( )
①AO=CO;②AC⊥BD;③AD∥BC;④∠CAB=∠CAD.
A.①和④ B.②和③ C.③和④ D.②和④
6.下列英语单词中,是中心对称图形的是( )
A.SOS B.CEO C.MBA D.SAR
7.如图,△ABC中,D是AB的中点,E在AC上,且∠AED=90°+∠C,则BC+2AE等于( )
A.AB B.AC C.AB D.AC
8.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OB
9.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AO=BO C.∠1=∠2 D.AC⊥BD
10.下列性质中,菱形对角线不具有的是( )
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
11.下列条件中,能判定一个四边形为菱形的条件是( )
A.对角线互相平分的四边形
B.对角线互相垂直且平分的四边形
C.对角线相等的四边形
D.对角线相等且互相垂直的四边形
12.在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H.这样得到的四边形EFGH中,是正方形的有( )
A.1个 B.2个 C.4个 D.无穷多个
二.填空题(共6小题,每题4分,共24分)
13.一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为 .
14.如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=125°,则∠BCE= 度.
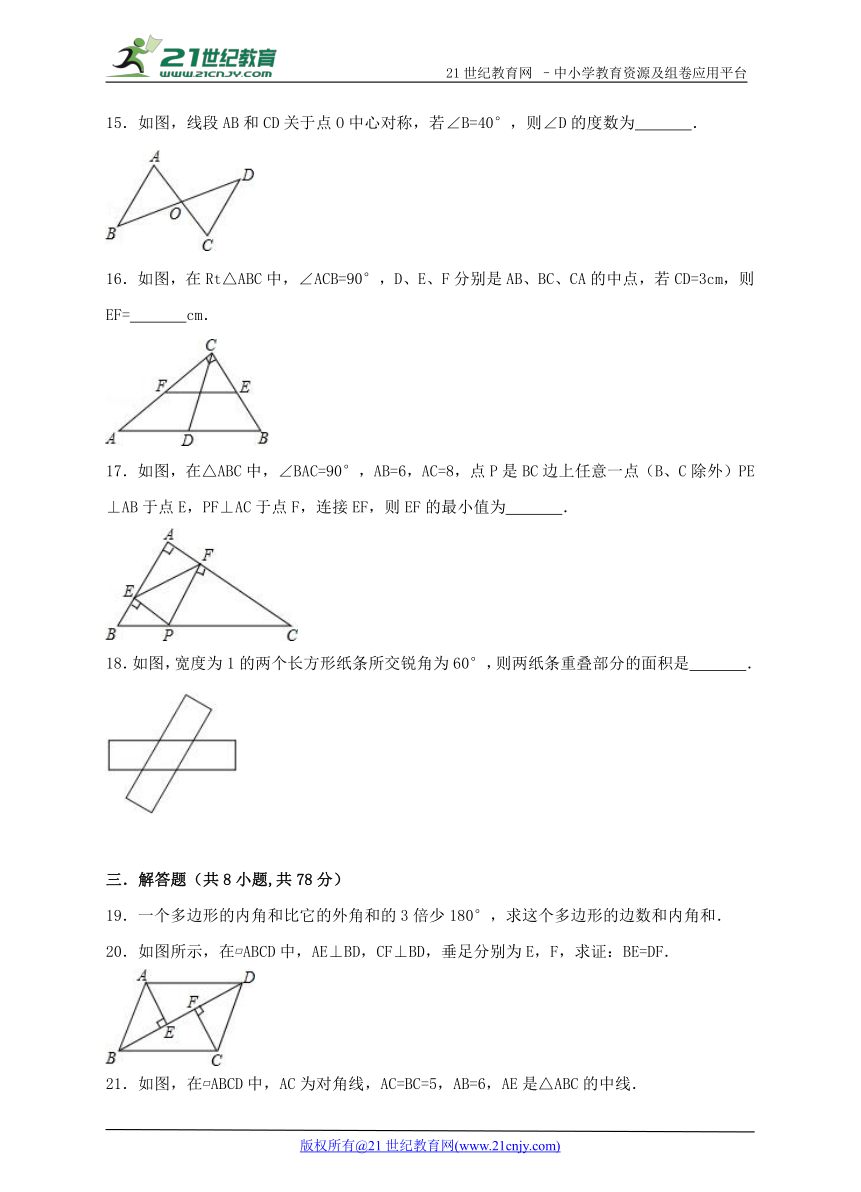
15.如图,线段AB和CD关于点O中心对称,若∠B=40°,则∠D的度数为 .
16.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=3cm,则EF= cm.
17.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为 .
18.如图,宽度为1的两个长方形纸条所交锐角为60°,则两纸条重叠部分的面积是 .
三.解答题(共8小题,共78分)
19.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和内角和.
20.如图所示,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:BE=DF.
21.如图,在 ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
22.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
23.如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.
24.正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
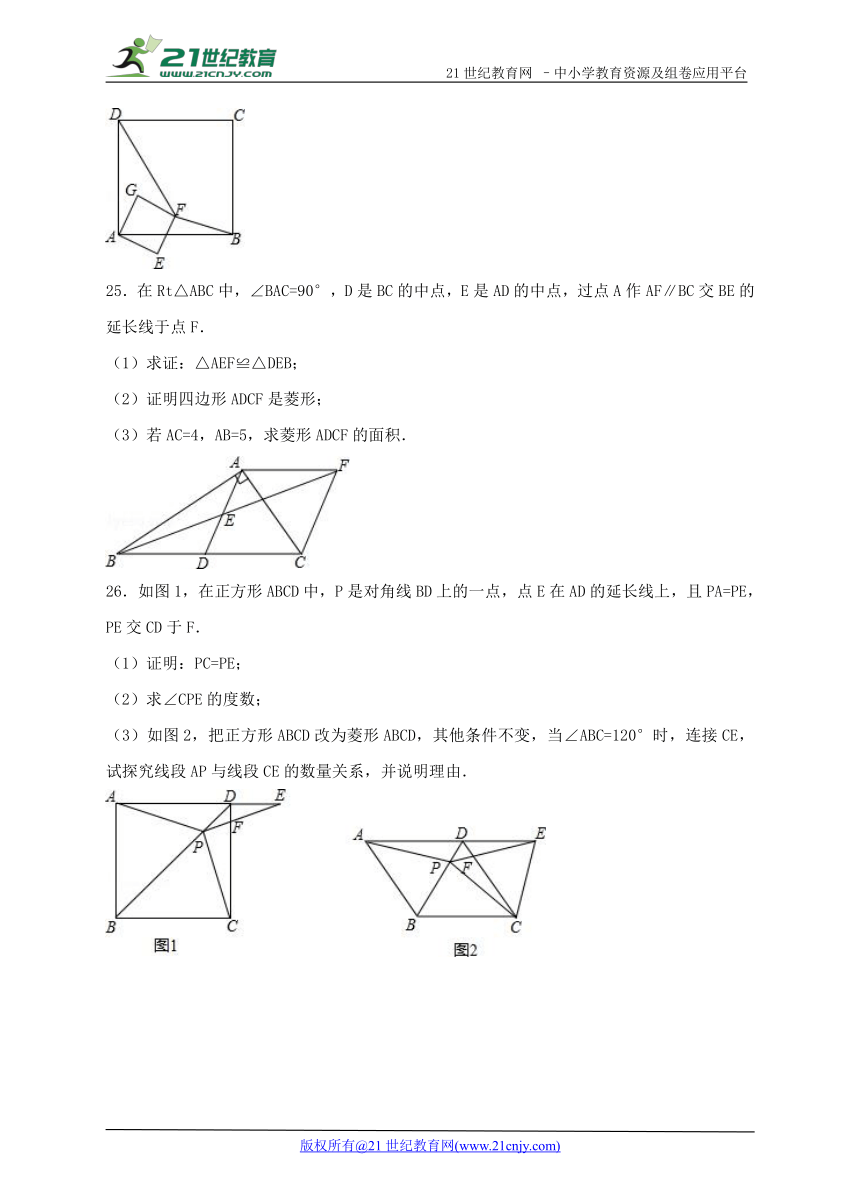
25.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
26.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
参考答案与试题解析
一.选择题(共12小题)
1.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
【分析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n﹣1)边形.
解:当剪去一个角后,剩下的部分是一个18边形,
则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.
故选A.
2.若一个多边形共有9条对角线,则它是( )边形.
A.五 B.六 C.七 D.八
【分析】根据多边形的对角线公式,列出方程求解即可.
解:设这个多边形是n边形,则=9,
∴n2﹣3n﹣9=0,
(n﹣6)(n+3)=0,
解得n=6,n=﹣3(舍去).
故选B.
3.一个四边形,截一刀后得到新多边形的内角和将( )
A.增加180° B.减少180°
C.不变 D.以上三种情况都有可能
【分析】根据一个四边形截一刀后得到的多边形的边数即可得出结果.
解:∵一个四边形截一刀后得到的多边形可能是三角形,可能是四边形,也可能是五边形,
∴内角和可能减少180°,可能不变,可能增加180°.
故选D.
4.在下列正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
【分析】正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
解:A、正方形的每个内角是90°,正八边形的每个内角是135°,由于90°+2×135°=360°,故能铺满;
B、正五边形和正八边形内角分别为108°、135°,显然不能构成360°的周角,故不能铺满;
C、正六边形和正三角形内角分别为120°、60°,由于60×4+120=360,故能铺满;
D、正三角形、正方形内角分别为60°、90°,由于60×3+90×2=360,故能铺满.
故选B.
5.如图,在平行四边形ABCD中,都不一定 成立的是( )
①AO=CO;②AC⊥BD;③AD∥BC;④∠CAB=∠CAD.
A.①和④ B.②和③ C.③和④ D.②和④
【分析】由四边形ABCD是平行四边形,即可得①和③正确,然后利用排除法即可求得答案.
解:∵四边形ABCD是平行四边形,
∴AO=CO,故①成立;
AD∥BC,故③成立;
利用排除法可得②与④不一定成立,
∵当四边形是菱形时,②和④成立.
故选D.
6.下列英语单词中,是中心对称图形的是( )
A.SOS B.CEO C.MBA D.SAR
【分析】把一个图形绕一点旋转180度,能够与原图形重合,则这个点就叫做对称点,这个图形就是中心对称图形,依据定义即可解决.
解:是中心对称图形的是A,故选A.
7.如图,△ABC中,D是AB的中点,E在AC上,且∠AED=90°+∠C,则BC+2AE等于( )
A.AB B.AC C.AB D.AC
【分析】如图,过点B作BF∥DE交AC于点F.则∠BFC=∠DEF.由三角形中位线的性质得到EF=AE.则由平行线的性质和邻补角的定义得到∠DEF=∠BFC=90°﹣∠C,即
∠FBC=∠BFC,等角对等边得到BC=FC,故BC+2AE=AC.
解:如图,过点B作BF∥DE交AC于点F.则∠BFC=∠DEF.
又∵点D是AB的中点,
∴EF=AE.
∵∠DEF=∠BFC=180°﹣∠AED=180°﹣(90°+∠C)=90°﹣∠C,
∴∠FBC=∠BFC,
∴BC=FC,
∴BC+2AE=AC.
故选B.
8.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OB
【分析】根据矩形的性质推出即可.
∵四边形ABCD是矩形,
∴AB∥DC,AC=BD,OA=OB,不能推出AC⊥BD,
∴选项A、B、D正确,选项C错误;
故选C.
9.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AO=BO C.∠1=∠2 D.AC⊥BD
【分析】根据矩形的判定定理(①有一个角是直角的平行四边形是矩形,②有三个角是直角的四边形是矩形,③对角线相等的平行四边形是矩形)逐一判断即可.
解:A、根据AB=BC和平行四边形ABCD不能得出四边形ABCD是矩形,故本选项错误;
B、∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AO=BO,
∴OA=OC=OB=OD,
即AC=BD,
∴平行四边形ABCD是矩形,故本选项正确;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB,
∴AB=BC,
∴四边形ABCD是菱形,不能推出四边形ABCD是矩形,故本选项错误;
D、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,不能推出四边形ABCD是矩形,故本选项错误;
故选B.
10.下列性质中,菱形对角线不具有的是( )
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
【分析】由菱形的对角线互相平分且垂直,可得菱形对角线所在直线是对称轴,继而求得答案.
解:∵菱形对角线具有的性质有:对角线互相垂直,对角线互相平分,
∴对角线所在直线是对称轴.
故A,B,D正确,C错误.
故选C.
11.下列条件中,能判定一个四边形为菱形的条件是( )
A.对角线互相平分的四边形
B.对角线互相垂直且平分的四边形
C.对角线相等的四边形
D.对角线相等且互相垂直的四边形
【分析】根据菱形的判定方法:对角线互相垂直平分来判断即可.
解:菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;
②四边相等;
③对角线互相垂直平分的四边形是菱形.只有B能判定为是菱形,
故选B.
12.在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H.这样得到的四边形EFGH中,是正方形的有( )
A.1个 B.2个 C.4个 D.无穷多个
【分析】在正方形四边上任意取点E、F、G、H,若能证明四边形EFGH为正方形,则说明可以得到无穷个正方形.
解:无穷多个.如图正方形ABCD:
AH=DG=CF=BE,HD=CG=FB=EA,∠A=∠B=∠C=∠D,
有△AEH≌△DHG≌△CGF≌△BFE,
则EH=HG=GF=FE,
另外 很容易得四个角均为90°
则四边形EHGF为正方形.
故选D.
二.填空题(共6小题)
13.一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为 15,16,17 .
【分析】先求出新多边形的边数,再根据截去一个角后的多边形与原多边形的边数相等,多1,少1三种情况进行讨论.
解:设新多边形的边数是n,则(n﹣2) 180°=2520°,
解得n=16,
∵截去一个角后的多边形与原多边形的边数可以相等,多1或少1,
∴原多边形的边数是15,16,17.
故答案为:15,16,17.
14.如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=125°,则∠BCE= 35 度.
【分析】根据平行四边形的性质和已知,可求出∠B,再进一步利用直角三角形的性质求解即可.
解:∵AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣125°=55°,
∵CE⊥AB,
∴在Rt△BCE中,∠BCE=90°﹣∠B=90°﹣55°=35°.
故答案为:35.
15.如图,线段AB和CD关于点O中心对称,若∠B=40°,则∠D的度数为 40° .
【分析】利用中心对称图形的性质得出△ABO≌△COD,得出∠B=∠D,进而得出答案.
解:∵线段AB和CD关于点O中心对称,∠B=40°,
∴△ABO≌△COD,
∴∠B=∠D,
∴∠D的度数为40°.
故答案为:40°.
16.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=3cm,则EF= 3 cm.
【分析】首先根据在直角三角形中,斜边上的中线等于斜边的一半可得AB=2CD=6cm,再根据中位线的性质可得EF=AB=3cm.
解:∵∠ACB=90°,D为AB中点,
∴AB=2CD,
∵CD=3cm,
∴AB=6cm,
∵E、F分别是BC、CA的中点,
∴EF=AB=3cm,
故答案为:3.
17.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为 4.8 .
【分析】连接AP,先由勾股定理求出BC,再证明四边形AEPF是矩形,得出对角线相等EF=AP,然后由AP⊥BC时,AP最小,根据面积求出AP即可.
解:连接AP,如图所示:
∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵PE⊥AB于点E,PF⊥AC,
∴∠AEP=∠AFP=90°,
∴四边形AEPF是矩形,
∴EF=AP,
当AP⊥BC时,AP最小,
此时∵BC AP=AB AC,
∴AP===4.8,
∴EF的最小值为4.8;
故答案为:4.8.
18.如图,宽度为1的两个长方形纸条所交锐角为60°,则两纸条重叠部分的面积是 .
【分析】根据题意可知:所得图形是菱形,设菱形ABCD,由已知得∠ABE=60°,过A作AE⊥BC于E,由勾股定理可求BE、AB、BC的长度,根据菱形的面积公式即可求出所填答案.
解:由题意可知:重叠部分是菱形,设菱形ABCD,则∠ABE=60°,
过A作AE⊥BC于E,则AE=1,
设BE=x,
∵∠ABE=60°,
∴∠BAE=30°,
∴AB=2x,
在△ABE中,∠AEB=90°,由勾股定理解得:x=,
∴AB=BC=,
∴重叠部分的面积是:×1=.
故答案为:.
三.解答题(共8小题)
19.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和内角和.
【分析】设这个多边形的边数为n,根据多边形的内角和公式(n﹣2) 180°与外角和定理列出方程,求解即可.
解:设这个多边形的边数为n,
根据题意,得(n﹣2)×180°=3×360°﹣180°,
解得n=7.
所以这个多边形的内角和为:(7﹣2) 180°=900°.
20.如图所示,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:BE=DF.
【分析】由在 ABCD中,AE⊥BD,CF⊥BD,利用AAS,易证得△ABE≌△CDF,然后由全等三角形的性质,证得结论.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF.
21.如图,在 ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
【分析】(1)连接BD,BD与AE交于点F,连接CF并延长到AB,与AB交于点H,则CH为△ABC的高;
(2)首先由三线合一,求得AH的长,再由勾股定理求得CH的长,继而求得△ABC的面积,又由AE是△ABC的中线,求得△ACE的面积.
解:(1)如图,连接BD,BD与AE交于点F,连接CF并延长到AB,则它与AB的交点即为H.
理由如下:
∵BD、AC是 ABCD的对角线,
∴点O是AC的中点,
∵AE、BO是等腰△ABC两腰上的中线,
∴AE=BO,AO=BE,
∵AB=BA,
∴△ABO≌△BAE(SSS),
∴∠ABO=∠BAE,
△ABF中,∵∠FAB=∠FBA,∴FA=FB,
∵∠BAC=∠ABC,
∴∠EAC=∠OBC,
由可得△AFC≌BFC(SAS)
∴∠ACF=∠BCF,即CH是等腰△ABC顶角平分线,
所以CH是△ABC的高;
(2)∵AC=BC=5,AB=6,CH⊥AB,
∴AH=AB=3,
∴CH==4,
∴S△ABC=AB CH=×6×4=12,
∵AE是△ABC的中线,
∴S△ACE=S△ABC=6.
22.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
【分析】(1)证明△ABN≌△ADN,即可得出结论;
(2)先判断MN是△BDC的中位线,从而得出CD,由(1)可得AD=AB=10,从而计算周长即可.
(1)证明:∵AN平分∠BAC
∴∠1=∠2
∵BN⊥AN
∴∠ANB=∠AND=90°
在△ABN和△ADN中,
∵,
∴△ABN≌△ADN(ASA),
∴BN=DN.
(2)解:∵△ABN≌△ADN,
∴AD=AB=10,
又∵点M是BC中点,
∴MN是△BDC的中位线,
∴CD=2MN=6,
故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.
23.如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.
【分析】(1)由MN∥BC,易得∠CBN=∠MNB,由已知∠PNB=3∠CBN,根据角的和差不难得出结论;
(2)连接AN,根据矩形的轴对称性,可知∠PAN=∠CBN,由(1)知∠PNM=2∠CBN=2∠PAN,由AD∥MN,可知∠PAN=∠ANM,所以∠PAN=∠PNA,根据等角对等边得到AP=PN,再用勾股定理列方程求出AP.
解:(1)∵四边形ABCD是矩形,M,N分别是AB,CD的中点,
∴MN∥BC,
∴∠CBN=∠MNB,
∵∠PNB=3∠CBN,
∴∠PNM=2∠CBN;
(2)连接AN,
根据矩形的轴对称性,可知∠PAN=∠CBN,
∵MN∥AD,
∴∠PAN=∠ANM,
由(1)知∠PNM=2∠CBN,
∴∠PAN=∠PNA,
∴AP=PN,
∵AB=CD=4,M,N分别为AB,CD的中点,
∴DN=2,
设AP=x,则PD=6﹣x,
在Rt△PDN中
PD2+DN2=PN2,
∴(6﹣x)2+22=x2,
解得:x=
所以AP=.
24.正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
【分析】(1)利用正方形的性质证明△DGF≌△BEF即可;
(2)当α=180°时,DF=BF.
(3)利用正方形的性质和△DGF≌△BEF的性质即可证得是真命题.
(1)证明:如图1,∵四边形ABCD和四边形AEFG为正方形,
∴AG=AE,AD=AB,GF=EF,∠DGF=∠BEF=90°,
∴DG=BE,
在△DGF和△BEF中,
,
∴△DGF≌△BEF(SAS),
∴DF=BF;
(2)解:图形(即反例)如图2,
(3)解:补充一个条件为:点F在正方形ABCD内;
即:若点F在正方形ABCD内,DF=BF,则旋转角α=0°.
25.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
【分析】(1)根据AAS证△AFE≌△DBE;
(2)利用①中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论;
(3)由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论.
(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=BC,
∴四边形ADCF是菱形;
(3)连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCF=AC DF=×4×5=10.
26.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【分析】(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法容易证明结论.
(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
第2章四边形单元检测基础卷
班级__________姓名____________总分___________
一.选择题(共12小题,每题4分,共48分)
1.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
2.若一个多边形共有9条对角线,则它是( )边形.
A.五 B.六 C.七 D.八
3.一个四边形,截一刀后得到新多边形的内角和将( )
A.增加180° B.减少180°
C.不变 D.以上三种情况都有可能
4.在下列正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
5.如图,在平行四边形ABCD中,都不一定 成立的是( )
①AO=CO;②AC⊥BD;③AD∥BC;④∠CAB=∠CAD.
A.①和④ B.②和③ C.③和④ D.②和④
6.下列英语单词中,是中心对称图形的是( )
A.SOS B.CEO C.MBA D.SAR
7.如图,△ABC中,D是AB的中点,E在AC上,且∠AED=90°+∠C,则BC+2AE等于( )
A.AB B.AC C.AB D.AC
8.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OB
9.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AO=BO C.∠1=∠2 D.AC⊥BD
10.下列性质中,菱形对角线不具有的是( )
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
11.下列条件中,能判定一个四边形为菱形的条件是( )
A.对角线互相平分的四边形
B.对角线互相垂直且平分的四边形
C.对角线相等的四边形
D.对角线相等且互相垂直的四边形
12.在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H.这样得到的四边形EFGH中,是正方形的有( )
A.1个 B.2个 C.4个 D.无穷多个
二.填空题(共6小题,每题4分,共24分)
13.一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为 .
14.如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=125°,则∠BCE= 度.
15.如图,线段AB和CD关于点O中心对称,若∠B=40°,则∠D的度数为 .
16.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=3cm,则EF= cm.
17.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为 .
18.如图,宽度为1的两个长方形纸条所交锐角为60°,则两纸条重叠部分的面积是 .
三.解答题(共8小题,共78分)
19.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和内角和.
20.如图所示,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:BE=DF.
21.如图,在 ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
22.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
23.如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.
24.正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
25.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
26.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
参考答案与试题解析
一.选择题(共12小题)
1.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16 B.17 C.18 D.19
【分析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n﹣1)边形.
解:当剪去一个角后,剩下的部分是一个18边形,
则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.
故选A.
2.若一个多边形共有9条对角线,则它是( )边形.
A.五 B.六 C.七 D.八
【分析】根据多边形的对角线公式,列出方程求解即可.
解:设这个多边形是n边形,则=9,
∴n2﹣3n﹣9=0,
(n﹣6)(n+3)=0,
解得n=6,n=﹣3(舍去).
故选B.
3.一个四边形,截一刀后得到新多边形的内角和将( )
A.增加180° B.减少180°
C.不变 D.以上三种情况都有可能
【分析】根据一个四边形截一刀后得到的多边形的边数即可得出结果.
解:∵一个四边形截一刀后得到的多边形可能是三角形,可能是四边形,也可能是五边形,
∴内角和可能减少180°,可能不变,可能增加180°.
故选D.
4.在下列正多边形组合中,不能铺满地面的是( )
A.正八边形和正方形 B.正五边形和正八边形
C.正六边形和正三角形 D.正三角形和正方形
【分析】正多边形的组合能否铺满地面,关键是看位于同一顶点处的几个角之和能否为360°.若能,则说明能铺满;反之,则说明不能铺满.
解:A、正方形的每个内角是90°,正八边形的每个内角是135°,由于90°+2×135°=360°,故能铺满;
B、正五边形和正八边形内角分别为108°、135°,显然不能构成360°的周角,故不能铺满;
C、正六边形和正三角形内角分别为120°、60°,由于60×4+120=360,故能铺满;
D、正三角形、正方形内角分别为60°、90°,由于60×3+90×2=360,故能铺满.
故选B.
5.如图,在平行四边形ABCD中,都不一定 成立的是( )
①AO=CO;②AC⊥BD;③AD∥BC;④∠CAB=∠CAD.
A.①和④ B.②和③ C.③和④ D.②和④
【分析】由四边形ABCD是平行四边形,即可得①和③正确,然后利用排除法即可求得答案.
解:∵四边形ABCD是平行四边形,
∴AO=CO,故①成立;
AD∥BC,故③成立;
利用排除法可得②与④不一定成立,
∵当四边形是菱形时,②和④成立.
故选D.
6.下列英语单词中,是中心对称图形的是( )
A.SOS B.CEO C.MBA D.SAR
【分析】把一个图形绕一点旋转180度,能够与原图形重合,则这个点就叫做对称点,这个图形就是中心对称图形,依据定义即可解决.
解:是中心对称图形的是A,故选A.
7.如图,△ABC中,D是AB的中点,E在AC上,且∠AED=90°+∠C,则BC+2AE等于( )
A.AB B.AC C.AB D.AC
【分析】如图,过点B作BF∥DE交AC于点F.则∠BFC=∠DEF.由三角形中位线的性质得到EF=AE.则由平行线的性质和邻补角的定义得到∠DEF=∠BFC=90°﹣∠C,即
∠FBC=∠BFC,等角对等边得到BC=FC,故BC+2AE=AC.
解:如图,过点B作BF∥DE交AC于点F.则∠BFC=∠DEF.
又∵点D是AB的中点,
∴EF=AE.
∵∠DEF=∠BFC=180°﹣∠AED=180°﹣(90°+∠C)=90°﹣∠C,
∴∠FBC=∠BFC,
∴BC=FC,
∴BC+2AE=AC.
故选B.
8.如图,在矩形ABCD中,对角线AC,BD交于点O,下列说法错误的是( )
A.AB∥DC B.AC=BD C.AC⊥BD D.OA=OB
【分析】根据矩形的性质推出即可.
∵四边形ABCD是矩形,
∴AB∥DC,AC=BD,OA=OB,不能推出AC⊥BD,
∴选项A、B、D正确,选项C错误;
故选C.
9.如图,要使 ABCD成为矩形,需添加的条件是( )
A.AB=BC B.AO=BO C.∠1=∠2 D.AC⊥BD
【分析】根据矩形的判定定理(①有一个角是直角的平行四边形是矩形,②有三个角是直角的四边形是矩形,③对角线相等的平行四边形是矩形)逐一判断即可.
解:A、根据AB=BC和平行四边形ABCD不能得出四边形ABCD是矩形,故本选项错误;
B、∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AO=BO,
∴OA=OC=OB=OD,
即AC=BD,
∴平行四边形ABCD是矩形,故本选项正确;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠2=∠ACB,
∵∠1=∠2,
∴∠1=∠ACB,
∴AB=BC,
∴四边形ABCD是菱形,不能推出四边形ABCD是矩形,故本选项错误;
D、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,不能推出四边形ABCD是矩形,故本选项错误;
故选B.
10.下列性质中,菱形对角线不具有的是( )
A.对角线互相垂直 B.对角线所在直线是对称轴
C.对角线相等 D.对角线互相平分
【分析】由菱形的对角线互相平分且垂直,可得菱形对角线所在直线是对称轴,继而求得答案.
解:∵菱形对角线具有的性质有:对角线互相垂直,对角线互相平分,
∴对角线所在直线是对称轴.
故A,B,D正确,C错误.
故选C.
11.下列条件中,能判定一个四边形为菱形的条件是( )
A.对角线互相平分的四边形
B.对角线互相垂直且平分的四边形
C.对角线相等的四边形
D.对角线相等且互相垂直的四边形
【分析】根据菱形的判定方法:对角线互相垂直平分来判断即可.
解:菱形的判定方法有三种:①定义:一组邻边相等的平行四边形是菱形;
②四边相等;
③对角线互相垂直平分的四边形是菱形.只有B能判定为是菱形,
故选B.
12.在正方形ABCD的边AB、BC、CD、DA上分别任意取点E、F、G、H.这样得到的四边形EFGH中,是正方形的有( )
A.1个 B.2个 C.4个 D.无穷多个
【分析】在正方形四边上任意取点E、F、G、H,若能证明四边形EFGH为正方形,则说明可以得到无穷个正方形.
解:无穷多个.如图正方形ABCD:
AH=DG=CF=BE,HD=CG=FB=EA,∠A=∠B=∠C=∠D,
有△AEH≌△DHG≌△CGF≌△BFE,
则EH=HG=GF=FE,
另外 很容易得四个角均为90°
则四边形EHGF为正方形.
故选D.
二.填空题(共6小题)
13.一个多边形截去一个角后,形成新多边形的内角和为2520°,则原多边形边数为 15,16,17 .
【分析】先求出新多边形的边数,再根据截去一个角后的多边形与原多边形的边数相等,多1,少1三种情况进行讨论.
解:设新多边形的边数是n,则(n﹣2) 180°=2520°,
解得n=16,
∵截去一个角后的多边形与原多边形的边数可以相等,多1或少1,
∴原多边形的边数是15,16,17.
故答案为:15,16,17.
14.如图,在平行四边形ABCD中,CE⊥AB,E为垂足.如果∠A=125°,则∠BCE= 35 度.
【分析】根据平行四边形的性质和已知,可求出∠B,再进一步利用直角三角形的性质求解即可.
解:∵AD∥BC,
∴∠A+∠B=180°,
∴∠B=180°﹣125°=55°,
∵CE⊥AB,
∴在Rt△BCE中,∠BCE=90°﹣∠B=90°﹣55°=35°.
故答案为:35.
15.如图,线段AB和CD关于点O中心对称,若∠B=40°,则∠D的度数为 40° .
【分析】利用中心对称图形的性质得出△ABO≌△COD,得出∠B=∠D,进而得出答案.
解:∵线段AB和CD关于点O中心对称,∠B=40°,
∴△ABO≌△COD,
∴∠B=∠D,
∴∠D的度数为40°.
故答案为:40°.
16.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=3cm,则EF= 3 cm.
【分析】首先根据在直角三角形中,斜边上的中线等于斜边的一半可得AB=2CD=6cm,再根据中位线的性质可得EF=AB=3cm.
解:∵∠ACB=90°,D为AB中点,
∴AB=2CD,
∵CD=3cm,
∴AB=6cm,
∵E、F分别是BC、CA的中点,
∴EF=AB=3cm,
故答案为:3.
17.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,点P是BC边上任意一点(B、C除外)PE⊥AB于点E,PF⊥AC于点F,连接EF,则EF的最小值为 4.8 .
【分析】连接AP,先由勾股定理求出BC,再证明四边形AEPF是矩形,得出对角线相等EF=AP,然后由AP⊥BC时,AP最小,根据面积求出AP即可.
解:连接AP,如图所示:
∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵PE⊥AB于点E,PF⊥AC,
∴∠AEP=∠AFP=90°,
∴四边形AEPF是矩形,
∴EF=AP,
当AP⊥BC时,AP最小,
此时∵BC AP=AB AC,
∴AP===4.8,
∴EF的最小值为4.8;
故答案为:4.8.
18.如图,宽度为1的两个长方形纸条所交锐角为60°,则两纸条重叠部分的面积是 .
【分析】根据题意可知:所得图形是菱形,设菱形ABCD,由已知得∠ABE=60°,过A作AE⊥BC于E,由勾股定理可求BE、AB、BC的长度,根据菱形的面积公式即可求出所填答案.
解:由题意可知:重叠部分是菱形,设菱形ABCD,则∠ABE=60°,
过A作AE⊥BC于E,则AE=1,
设BE=x,
∵∠ABE=60°,
∴∠BAE=30°,
∴AB=2x,
在△ABE中,∠AEB=90°,由勾股定理解得:x=,
∴AB=BC=,
∴重叠部分的面积是:×1=.
故答案为:.
三.解答题(共8小题)
19.一个多边形的内角和比它的外角和的3倍少180°,求这个多边形的边数和内角和.
【分析】设这个多边形的边数为n,根据多边形的内角和公式(n﹣2) 180°与外角和定理列出方程,求解即可.
解:设这个多边形的边数为n,
根据题意,得(n﹣2)×180°=3×360°﹣180°,
解得n=7.
所以这个多边形的内角和为:(7﹣2) 180°=900°.
20.如图所示,在 ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:BE=DF.
【分析】由在 ABCD中,AE⊥BD,CF⊥BD,利用AAS,易证得△ABE≌△CDF,然后由全等三角形的性质,证得结论.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF.
21.如图,在 ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线.
(1)用无刻度的直尺画出△ABC的高CH(保留画图痕迹);
(2)求△ACE的面积.
【分析】(1)连接BD,BD与AE交于点F,连接CF并延长到AB,与AB交于点H,则CH为△ABC的高;
(2)首先由三线合一,求得AH的长,再由勾股定理求得CH的长,继而求得△ABC的面积,又由AE是△ABC的中线,求得△ACE的面积.
解:(1)如图,连接BD,BD与AE交于点F,连接CF并延长到AB,则它与AB的交点即为H.
理由如下:
∵BD、AC是 ABCD的对角线,
∴点O是AC的中点,
∵AE、BO是等腰△ABC两腰上的中线,
∴AE=BO,AO=BE,
∵AB=BA,
∴△ABO≌△BAE(SSS),
∴∠ABO=∠BAE,
△ABF中,∵∠FAB=∠FBA,∴FA=FB,
∵∠BAC=∠ABC,
∴∠EAC=∠OBC,
由可得△AFC≌BFC(SAS)
∴∠ACF=∠BCF,即CH是等腰△ABC顶角平分线,
所以CH是△ABC的高;
(2)∵AC=BC=5,AB=6,CH⊥AB,
∴AH=AB=3,
∴CH==4,
∴S△ABC=AB CH=×6×4=12,
∵AE是△ABC的中线,
∴S△ACE=S△ABC=6.
22.如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
(1)求证:BN=DN;
(2)求△ABC的周长.
【分析】(1)证明△ABN≌△ADN,即可得出结论;
(2)先判断MN是△BDC的中位线,从而得出CD,由(1)可得AD=AB=10,从而计算周长即可.
(1)证明:∵AN平分∠BAC
∴∠1=∠2
∵BN⊥AN
∴∠ANB=∠AND=90°
在△ABN和△ADN中,
∵,
∴△ABN≌△ADN(ASA),
∴BN=DN.
(2)解:∵△ABN≌△ADN,
∴AD=AB=10,
又∵点M是BC中点,
∴MN是△BDC的中位线,
∴CD=2MN=6,
故△ABC的周长=AB+BC+CD+AD=10+15+6+10=41.
23.如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.
【分析】(1)由MN∥BC,易得∠CBN=∠MNB,由已知∠PNB=3∠CBN,根据角的和差不难得出结论;
(2)连接AN,根据矩形的轴对称性,可知∠PAN=∠CBN,由(1)知∠PNM=2∠CBN=2∠PAN,由AD∥MN,可知∠PAN=∠ANM,所以∠PAN=∠PNA,根据等角对等边得到AP=PN,再用勾股定理列方程求出AP.
解:(1)∵四边形ABCD是矩形,M,N分别是AB,CD的中点,
∴MN∥BC,
∴∠CBN=∠MNB,
∵∠PNB=3∠CBN,
∴∠PNM=2∠CBN;
(2)连接AN,
根据矩形的轴对称性,可知∠PAN=∠CBN,
∵MN∥AD,
∴∠PAN=∠ANM,
由(1)知∠PNM=2∠CBN,
∴∠PAN=∠PNA,
∴AP=PN,
∵AB=CD=4,M,N分别为AB,CD的中点,
∴DN=2,
设AP=x,则PD=6﹣x,
在Rt△PDN中
PD2+DN2=PN2,
∴(6﹣x)2+22=x2,
解得:x=
所以AP=.
24.正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图.
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由.
【分析】(1)利用正方形的性质证明△DGF≌△BEF即可;
(2)当α=180°时,DF=BF.
(3)利用正方形的性质和△DGF≌△BEF的性质即可证得是真命题.
(1)证明:如图1,∵四边形ABCD和四边形AEFG为正方形,
∴AG=AE,AD=AB,GF=EF,∠DGF=∠BEF=90°,
∴DG=BE,
在△DGF和△BEF中,
,
∴△DGF≌△BEF(SAS),
∴DF=BF;
(2)解:图形(即反例)如图2,
(3)解:补充一个条件为:点F在正方形ABCD内;
即:若点F在正方形ABCD内,DF=BF,则旋转角α=0°.
25.在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
【分析】(1)根据AAS证△AFE≌△DBE;
(2)利用①中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论;
(3)由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论.
(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
,
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=BC,
∴四边形ADCF是菱形;
(3)连接DF,
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S菱形ADCF=AC DF=×4×5=10.
26.如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【分析】(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法容易证明结论.
(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
