高中数学必修二 1.3.2球的体积和表面积 课件 (2)
文档属性
| 名称 | 高中数学必修二 1.3.2球的体积和表面积 课件 (2) |  | |
| 格式 | zip | ||
| 文件大小 | 683.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-28 19:59:07 | ||
图片预览








文档简介
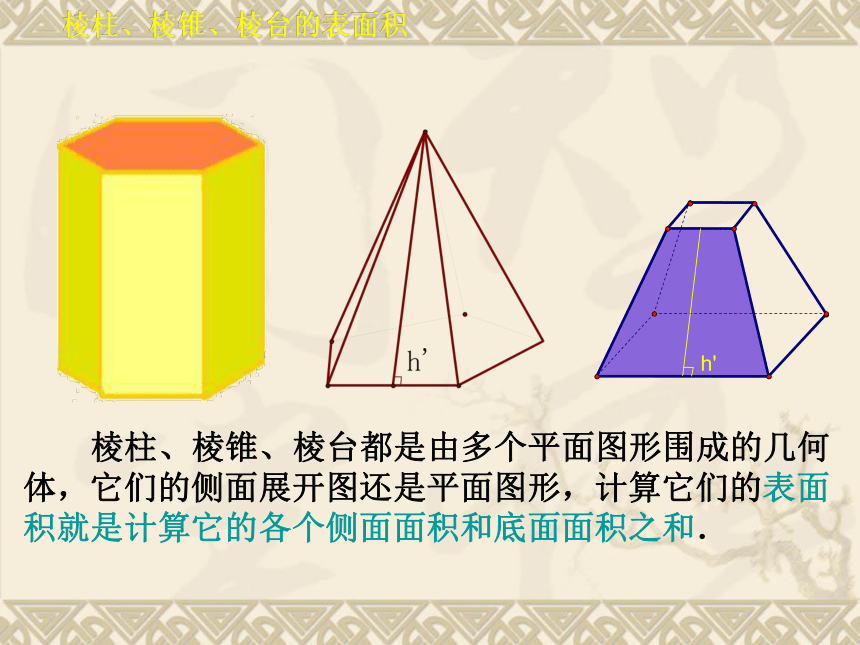
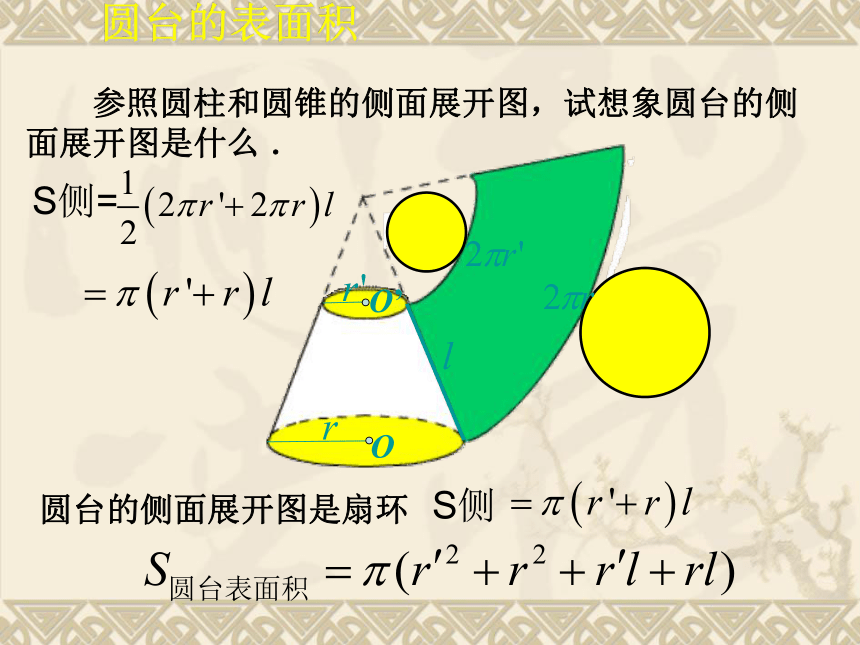
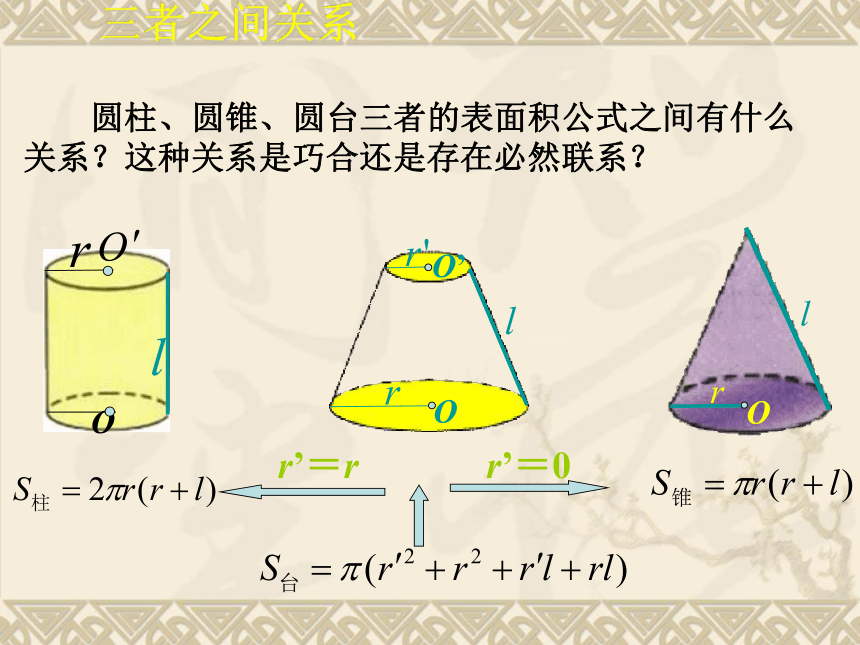
课件40张PPT。1.3.2球的体积和表面积上节知识回顾柱、锥、台的表面积和体积公式都可以有台体的表面积和体积特殊化得到棱柱、棱锥、棱台的表面积 棱柱、棱锥、棱台都是由多个平面图形围成的几何体,它们的侧面展开图还是平面图形,计算它们的表面积就是计算它的各个侧面面积和底面面积之和.圆台的表面积 参照圆柱和圆锥的侧面展开图,试想象圆台的侧面展开图是什么 .圆台的侧面展开图是扇环S侧S侧=三者之间关系 圆柱、圆锥、圆台三者的表面积公式之间有什么关系?这种关系是巧合还是存在必然联系?棱柱、棱锥和棱台的体积公式:
v=
当s=s‘时为柱体体积公式v=sh.
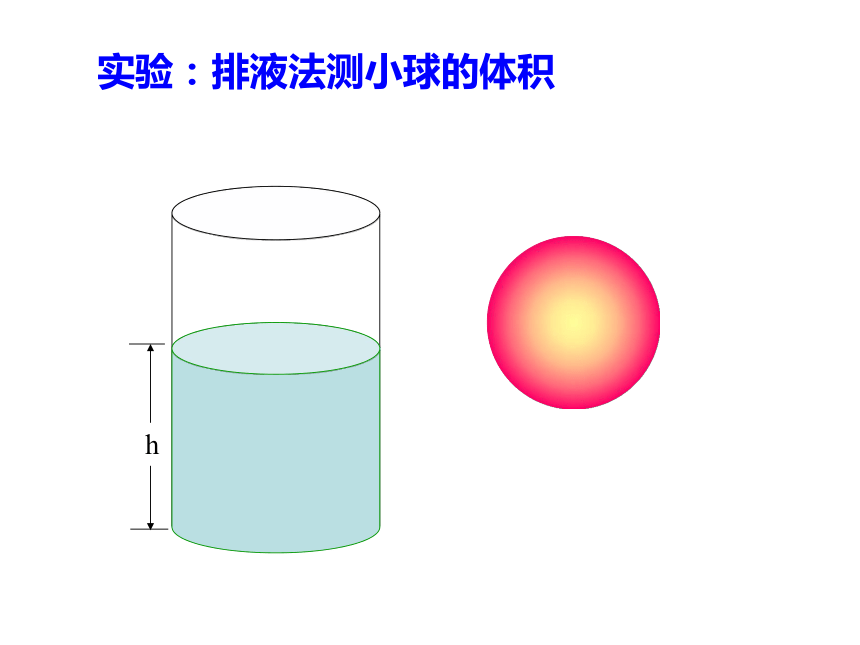
当s ‘ =0为锥体体积公式v= 怎样求球的体积?实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积H小球的体积
等于
它排开液体的体积实验:排液法测小球的体积曹冲称象假设将圆n等分,则A2A1AnOA3回顾圆面积公式的推导 割 圆 术 早在公元三世纪,我国数学家刘徽为推导圆的面积公式而发明了“倍边法割圆术”。他用加倍的方式不断增加圆内接正多边形的边数,使其面积与圆的面积之差更小,即所谓“割之弥细,所失弥小”。这样重复下去,就达到了“割之又割,以至于不可再割,则与圆合体而无所失矣”。这是世界上最早的
“极限”思想。了解:已知球的半径为R,用R表示球的体积.2.球的体积OROA球的体积定理:半径是R的球的体积注:推导过程不要求,只需了解高等于底面半径的旋转体体积对比阅读材料以及思考题1.球的直径伸长为原来的2倍,体积变为原来的几倍?
2.一个正方体的顶点都在球面上,它的棱长是4cm,求这个球的体积. 课堂练习8倍 钢球直径是5cm,.把钢球放入一个正方体的有盖纸盒中,至少要用多少纸?用料最省时,球与正方体有什么位置关系?球内切于正方体侧棱长为5cm两个几何体相(内)切:
一个几何体的各个面与另一个几何体的各面相切.两个几何体相接:
一个几何体的所有顶点都 在另一个几何体的表面上 球面不能展开成平面图形,所以
求球的表面积无法用展开图求出,
如何求球的表面积公式呢? 回忆球的体积公式的推导方法, 得到启发,可以借助极限思想方法来推导球的表面积公式。. 球的表面积.球面:半圆以它的直径为旋转轴,旋转所成的曲面。球(即球体):球面所围成的几何体。它包括球面和球面所包围的空间。半径是R的球的体积:球的表面积注:推导过程不要求,只需了解
第一步:分割球面被分割成n个网格,表面积分别为:则球的体积为:球的表面积 球的表面积是大圆面积的4倍R?注:推导过程不要求,只需了解
1、地球和火星都可以看作近似球体,地球半径约为6370km,火星的直径约为地球的一半。
求地球的表面积和体积;
火星的表面积约为地球表面积的几分之几?体积呢?课堂练习解:(1)(2)例1.如图,圆柱的底面直径与高都等于球的直径,求证:
(1)球的表面积等于圆柱的侧面积.
(2)球的表面积等于圆柱全面积的三分之二.证明:(2)例2.如图,已知球O的半径为R,正方体ABCD-A1B1C1D1的棱长 为a,它的各个顶点都在球O的球面上,
求证:分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O切于这个正方体的六个面,则有R=————。
。
1、一个四面体的所有的棱都为 ,四个顶点在同一球面上,则此球的表面积( )A 3лB 4лC D 6л●●C 解:设四面体为ABCD, 为其外接球心。 球半径为R,O为A在平面BCD上的射影,M为CD的中点。连结BA
1、一个四面体的所有的棱都为 ,四个顶点在同一球面上,则此球的表面积( )A 3лB 4лC D 6л 解法2 构造棱长为1的正方体,如图。则A1、C1、B、D是棱长为 的正四面体的顶点。正方体的外接球也是正四面体的外接球,此时球的直径为 ,选A
2、若正四体的棱长都为6,内有一球与四个面都相切,求球的表面积。 解:作出过一条侧棱PC和高PO的截面,则截面三角形PDC的边PD是斜高,DC是斜高的射影,球被截成的大圆与DP、DC相切,连结EO,设球半径为r,
2、若正四体的棱长都为6,内有一球与四个面都相切,求球的表面积。解法2:连结OA、OB、OC、OP,那么
解题小结:1、多面体的“切”、“接”问题,必须明确“切”、“接”位置和有关元素间的数量关系,常借助“截面”图形来解决。2、正三棱锥、正四面体是重要的基本图形,要掌握其中的边、角关系。能将空间问题化为平面问题得到解决,并注意方程思想的应用。3、注意化整为零的思想的应用。4、正四面体的内切球半径等于其高的四分之一,外接球半径等于其高的四分之三。小结:(1)有关球和球面的概念。(2)球的体积公式:
球的表面积公式:(3)用“分割-求近似和-化为准确和”
的数学方法推出了球的体积和表面积公式:(4)球的体积公式和表面积的一些运用。作业1.习题1.3
2.导与练
v=
当s=s‘时为柱体体积公式v=sh.
当s ‘ =0为锥体体积公式v= 怎样求球的体积?实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积实验:排液法测小球的体积H小球的体积
等于
它排开液体的体积实验:排液法测小球的体积曹冲称象假设将圆n等分,则A2A1AnOA3回顾圆面积公式的推导 割 圆 术 早在公元三世纪,我国数学家刘徽为推导圆的面积公式而发明了“倍边法割圆术”。他用加倍的方式不断增加圆内接正多边形的边数,使其面积与圆的面积之差更小,即所谓“割之弥细,所失弥小”。这样重复下去,就达到了“割之又割,以至于不可再割,则与圆合体而无所失矣”。这是世界上最早的
“极限”思想。了解:已知球的半径为R,用R表示球的体积.2.球的体积OROA球的体积定理:半径是R的球的体积注:推导过程不要求,只需了解高等于底面半径的旋转体体积对比阅读材料以及思考题1.球的直径伸长为原来的2倍,体积变为原来的几倍?
2.一个正方体的顶点都在球面上,它的棱长是4cm,求这个球的体积. 课堂练习8倍 钢球直径是5cm,.把钢球放入一个正方体的有盖纸盒中,至少要用多少纸?用料最省时,球与正方体有什么位置关系?球内切于正方体侧棱长为5cm两个几何体相(内)切:
一个几何体的各个面与另一个几何体的各面相切.两个几何体相接:
一个几何体的所有顶点都 在另一个几何体的表面上 球面不能展开成平面图形,所以
求球的表面积无法用展开图求出,
如何求球的表面积公式呢? 回忆球的体积公式的推导方法, 得到启发,可以借助极限思想方法来推导球的表面积公式。. 球的表面积.球面:半圆以它的直径为旋转轴,旋转所成的曲面。球(即球体):球面所围成的几何体。它包括球面和球面所包围的空间。半径是R的球的体积:球的表面积注:推导过程不要求,只需了解
第一步:分割球面被分割成n个网格,表面积分别为:则球的体积为:球的表面积 球的表面积是大圆面积的4倍R?注:推导过程不要求,只需了解
1、地球和火星都可以看作近似球体,地球半径约为6370km,火星的直径约为地球的一半。
求地球的表面积和体积;
火星的表面积约为地球表面积的几分之几?体积呢?课堂练习解:(1)(2)例1.如图,圆柱的底面直径与高都等于球的直径,求证:
(1)球的表面积等于圆柱的侧面积.
(2)球的表面积等于圆柱全面积的三分之二.证明:(2)例2.如图,已知球O的半径为R,正方体ABCD-A1B1C1D1的棱长 为a,它的各个顶点都在球O的球面上,
求证:分析:正方体内接于球,则由球和正方体都是中心对称图形可知,它们中心重合,则正方体对角线与球的直径相等。略解:变题1.如果球O切于这个正方体的六个面,则有R=————。
。
1、一个四面体的所有的棱都为 ,四个顶点在同一球面上,则此球的表面积( )A 3лB 4лC D 6л●●C 解:设四面体为ABCD, 为其外接球心。 球半径为R,O为A在平面BCD上的射影,M为CD的中点。连结BA
1、一个四面体的所有的棱都为 ,四个顶点在同一球面上,则此球的表面积( )A 3лB 4лC D 6л 解法2 构造棱长为1的正方体,如图。则A1、C1、B、D是棱长为 的正四面体的顶点。正方体的外接球也是正四面体的外接球,此时球的直径为 ,选A
2、若正四体的棱长都为6,内有一球与四个面都相切,求球的表面积。 解:作出过一条侧棱PC和高PO的截面,则截面三角形PDC的边PD是斜高,DC是斜高的射影,球被截成的大圆与DP、DC相切,连结EO,设球半径为r,
2、若正四体的棱长都为6,内有一球与四个面都相切,求球的表面积。解法2:连结OA、OB、OC、OP,那么
解题小结:1、多面体的“切”、“接”问题,必须明确“切”、“接”位置和有关元素间的数量关系,常借助“截面”图形来解决。2、正三棱锥、正四面体是重要的基本图形,要掌握其中的边、角关系。能将空间问题化为平面问题得到解决,并注意方程思想的应用。3、注意化整为零的思想的应用。4、正四面体的内切球半径等于其高的四分之一,外接球半径等于其高的四分之三。小结:(1)有关球和球面的概念。(2)球的体积公式:
球的表面积公式:(3)用“分割-求近似和-化为准确和”
的数学方法推出了球的体积和表面积公式:(4)球的体积公式和表面积的一些运用。作业1.习题1.3
2.导与练
