高中数学必修二 2.1.2空间中直线与直线之间的位置关系 课件 (2)
文档属性
| 名称 | 高中数学必修二 2.1.2空间中直线与直线之间的位置关系 课件 (2) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-28 20:07:13 | ||
图片预览








文档简介
课件23张PPT。2.1.2空间中直线与
直线之间的位置关系判断下列命题对错:
1.如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2.将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3.四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4.一条直线和一个点可以确定一个平面。( )
5.如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )?????温故知新复习:平面内两条直线的位置关系相交直线
(有一个公共点)平行直线
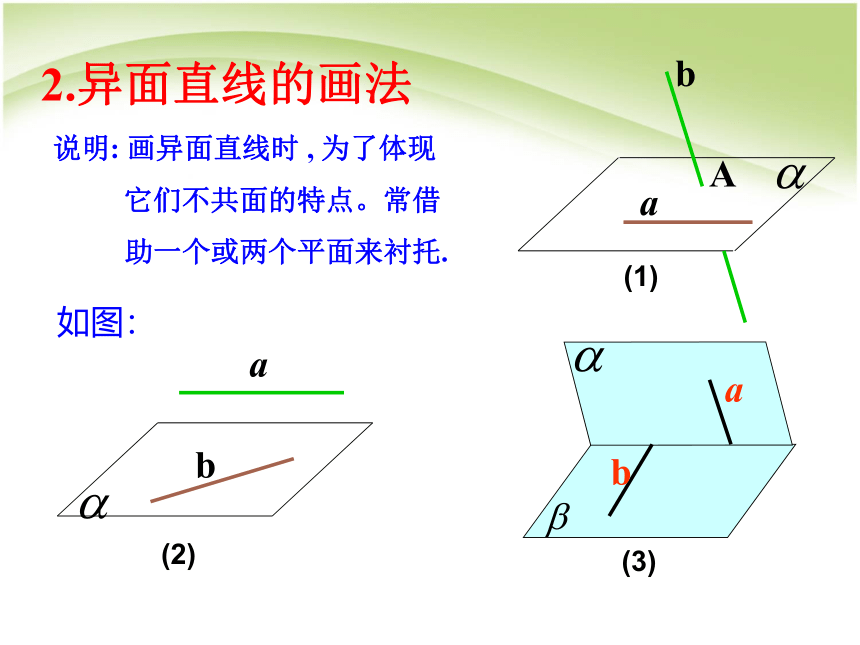
(无公共点)两路相交立交桥立交桥中, 两条路线AB, CD既不平行,又不相交观察实例 不同在任何一个平面内的两条直线叫做异面直线。没有只有一个没有共面不共面共面1.异面直线的定义2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
助一个或两个平面来衬托.如图:(1)(3)(2)a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线是否一定异面?思考 按是否在
同一平面内分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点:按公共点个数分相交直线无公共点平行直线异面直线空间直线与直线之间的位置关系3.异面直线的判定方法:(1)定义法:由定义判定两直线不可能在同一平面内.(借助反证法)(2)判定定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线(1)在如图所示的正方体中,指出哪些
棱所在的直线与直线BA1是异面直线?ABCDA1B1D1C1⑵已知M、N分别是长方体的棱C1D1与CC1
上的点,那么MN与AB所在的直线相交吗?ABCDA1B1D1C1MN公理4 平行于同一条直线的两条直线互相平行.注:
1.直线a,b,c 两两平行,可记为a // b // c .2.公理4所表述的性质,叫做空间平行线的传递性.3.证明空间两直线平行 的方法:
(1) 定义法:一要证两直线在同一平面内;二要证两直线没有公共点(反证法)
(2) 公理法平行公理例2 如图,空间四边行ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.D变式:如果再加上条件AC=BD,那么四边形EFGH是什么图形? 立体问题平面化是解立体几何时最主要、最常用的一种方法。等角定理1:如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补.推论:如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等.等角定理如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角.?任选若两条异面直线所成角为90°,则称它们互相垂直.异面直线a与b垂直也记作a⊥b.平移4.两条异面直线所成的角注1:异面直线a、b所成角,只与a、b的相互位置有关, 而与点O位置无关.一般常把点O取在直线a或b上.注2:异面直线所成角的取值范围:注3:求异面直线所所成角的步骤:
一作、二证、三求解例1 如图表示一个正方体:(1)求直线BA1与CC1的夹角的度数.(2)哪些棱所在的直线与直线AA1垂直?典例剖析例2 如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值.CBADA1B1C1D1典例剖析aa小结:典例赏析作业:1.阅读教材第44页至第47页;2.在课本上完成:
习题2.1 A组 3,4,5,7,8题; B组13.书面作业:
习题2.1 A组5,6;补充作业:(见下页)补充作业
直线之间的位置关系判断下列命题对错:
1.如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。( )
2.将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。 ( )
3.四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。 ( )
4.一条直线和一个点可以确定一个平面。( )
5.如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。 ( )?????温故知新复习:平面内两条直线的位置关系相交直线
(有一个公共点)平行直线
(无公共点)两路相交立交桥立交桥中, 两条路线AB, CD既不平行,又不相交观察实例 不同在任何一个平面内的两条直线叫做异面直线。没有只有一个没有共面不共面共面1.异面直线的定义2.异面直线的画法说明: 画异面直线时 , 为了体现
它们不共面的特点。常借
助一个或两个平面来衬托.如图:(1)(3)(2)a与b是相交直线a与b是平行直线a与b是异面直线答:不一定:它们可能异面,可能相交,也可能平行。 分别在两个平面内的两条直线是否一定异面?思考 按是否在
同一平面内分同在一个平面内相交直线平行直线 不同在任何一个平面内:异面直线 有一个公共点:按公共点个数分相交直线无公共点平行直线异面直线空间直线与直线之间的位置关系3.异面直线的判定方法:(1)定义法:由定义判定两直线不可能在同一平面内.(借助反证法)(2)判定定理:过平面外一点与平面内一点的直线,和平面内不经过该点的直线是异面直线(1)在如图所示的正方体中,指出哪些
棱所在的直线与直线BA1是异面直线?ABCDA1B1D1C1⑵已知M、N分别是长方体的棱C1D1与CC1
上的点,那么MN与AB所在的直线相交吗?ABCDA1B1D1C1MN公理4 平行于同一条直线的两条直线互相平行.注:
1.直线a,b,c 两两平行,可记为a // b // c .2.公理4所表述的性质,叫做空间平行线的传递性.3.证明空间两直线平行 的方法:
(1) 定义法:一要证两直线在同一平面内;二要证两直线没有公共点(反证法)
(2) 公理法平行公理例2 如图,空间四边行ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.D变式:如果再加上条件AC=BD,那么四边形EFGH是什么图形? 立体问题平面化是解立体几何时最主要、最常用的一种方法。等角定理1:如果一个角的两边和另一个角的两边分别对应平行,那么这两个角相等或互补.推论:如果一个角的两边和另一个角的两边分别平行且方向相同,那么这两个角相等.等角定理如图所示,a,b是两条异面直线,在空间中任选一点O,过O点分别作 a,b的平行线 a′和 b′,a′b′ 则这两条线所成的锐角θ(或直角),θ 称为异面直线a,b所成的角.?任选若两条异面直线所成角为90°,则称它们互相垂直.异面直线a与b垂直也记作a⊥b.平移4.两条异面直线所成的角注1:异面直线a、b所成角,只与a、b的相互位置有关, 而与点O位置无关.一般常把点O取在直线a或b上.注2:异面直线所成角的取值范围:注3:求异面直线所所成角的步骤:
一作、二证、三求解例1 如图表示一个正方体:(1)求直线BA1与CC1的夹角的度数.(2)哪些棱所在的直线与直线AA1垂直?典例剖析例2 如图,在长方体中,已知AA1=AD=a,
AB= a,求AB1与BC1所成的角的余弦值.CBADA1B1C1D1典例剖析aa小结:典例赏析作业:1.阅读教材第44页至第47页;2.在课本上完成:
习题2.1 A组 3,4,5,7,8题; B组13.书面作业:
习题2.1 A组5,6;补充作业:(见下页)补充作业
