高中数学必修二 2.2.1_直线与平面平行的判定 课件 (2)
文档属性
| 名称 | 高中数学必修二 2.2.1_直线与平面平行的判定 课件 (2) |

|
|
| 格式 | zip | ||
| 文件大小 | 567.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-28 00:00:00 | ||
图片预览



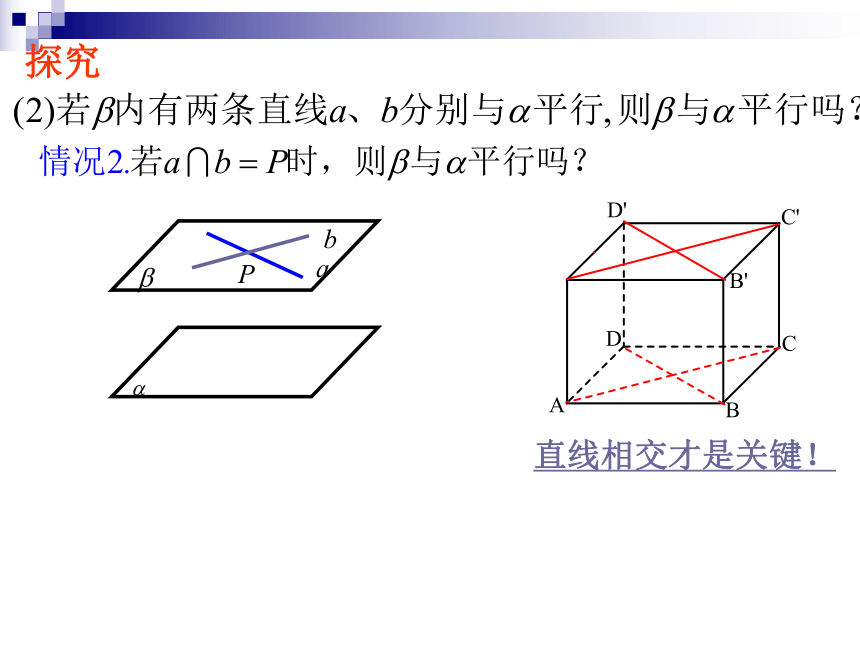
文档简介
课件33张PPT。
2.2.1 直线与平面平行的判定定理
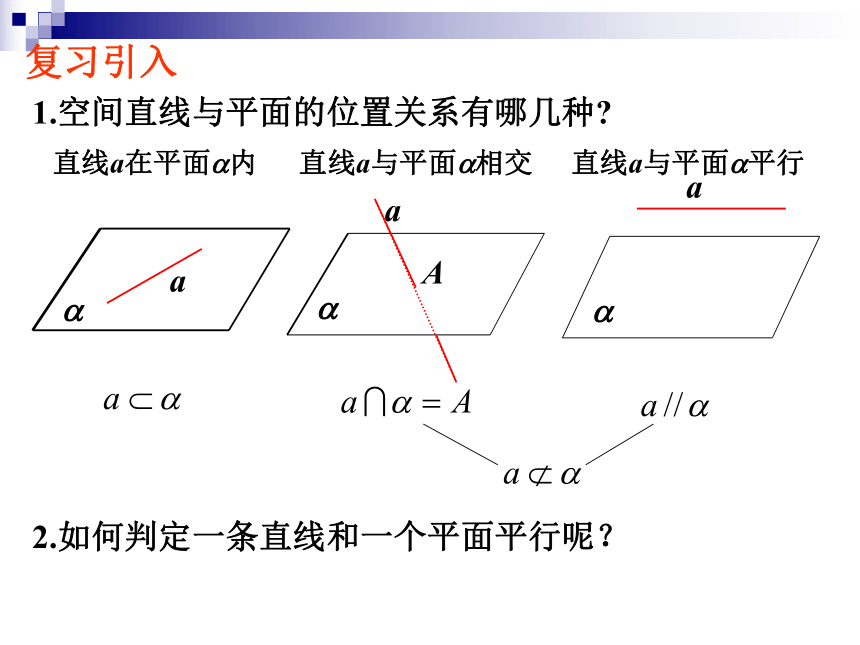
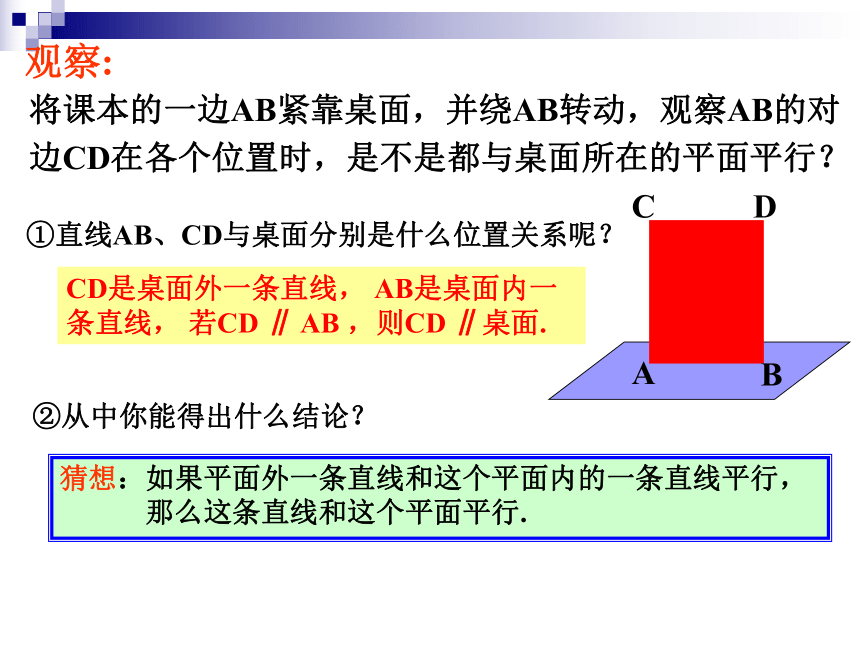
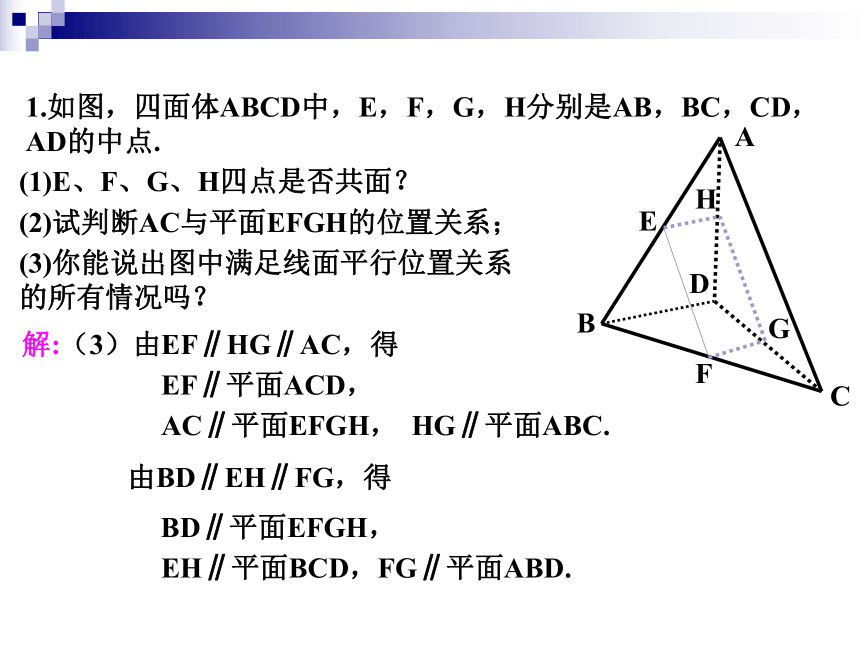
2.2.2平面与平面平行的判定定理1.空间直线与平面的位置关系有哪几种?2.如何判定一条直线和一个平面平行呢?复习引入将课本的一边AB紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行?②从中你能得出什么结论?ABCDCD是桌面外一条直线, AB是桌面内一条直线, 若CD ∥ AB ,则CD ∥桌面.①直线AB、CD与桌面分别是什么位置关系呢?猜想:如果平面外一条直线和这个平面内的一条直线平行, 那么这条直线和这个平面平行.观察:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.(2)该定理作用:“线线平行?线面平行”——空间问题“平面化”即1.直线与平面平行的判定定理(1)用该定理判断直线a和平面?平行,须具备三个条件: “面外、面内、平行”(3)应用该定理,关键是在平面?内找到一条直线与已知直线a平行.已知:空间四边形ABCD中,E、F分别是AB、AD的中点.
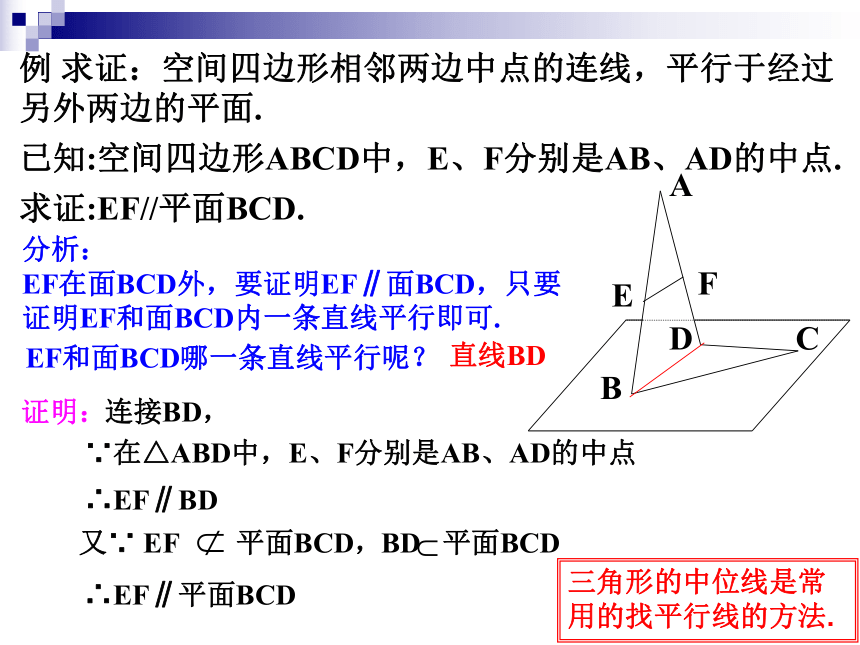
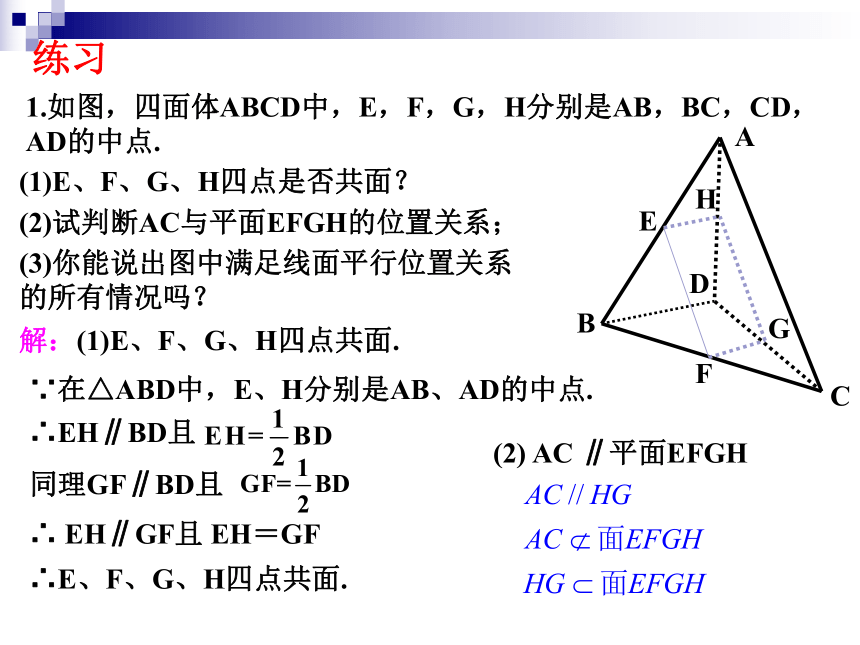
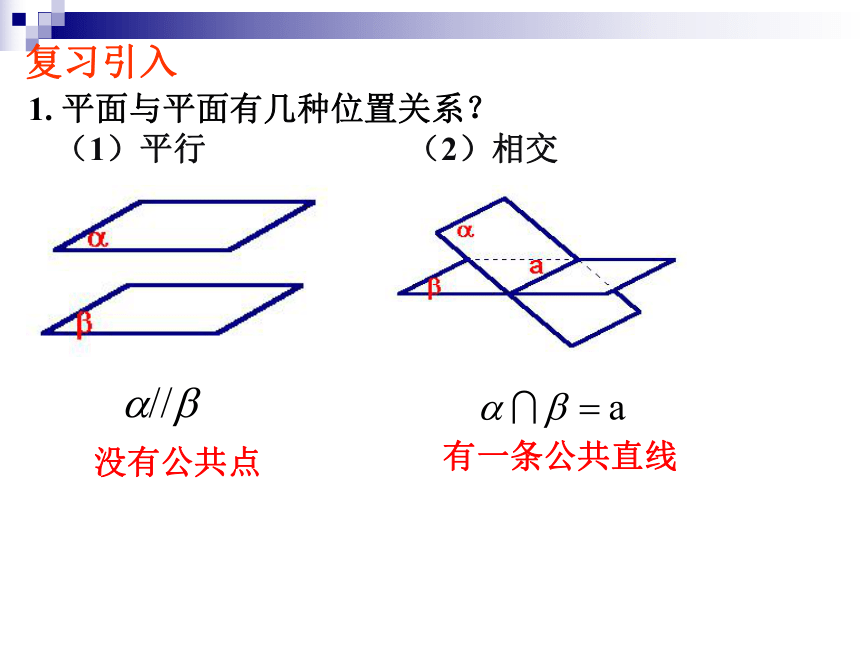
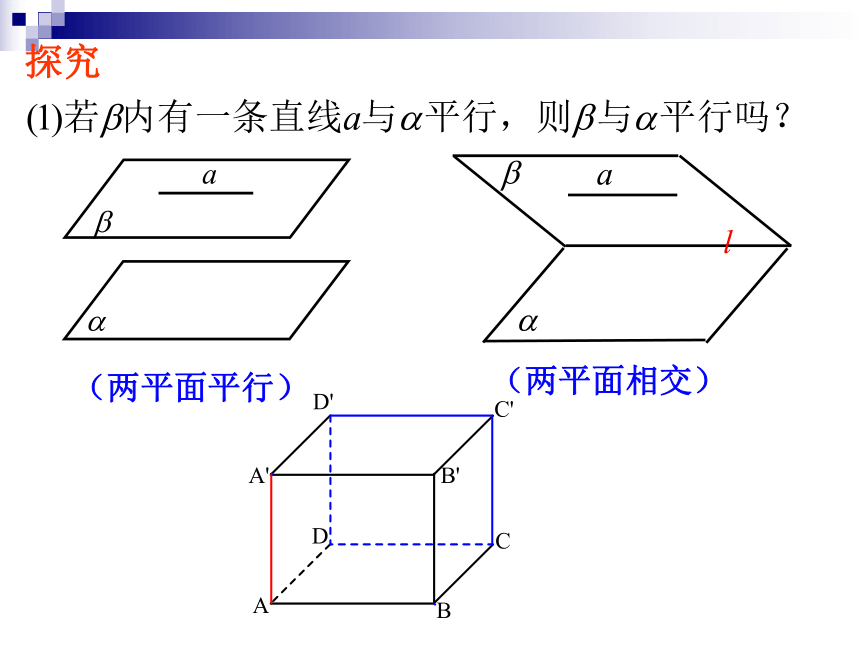
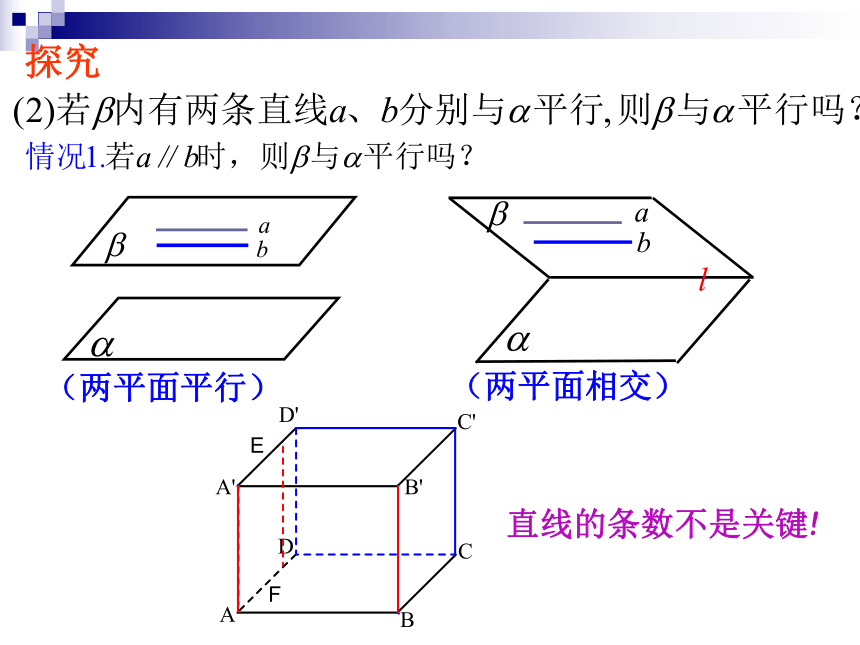
求证:EF//平面BCD.分析: EF在面BCD外,要证明EF∥面BCD,只要证明EF和面BCD内一条直线平行即可.EF和面BCD哪一条直线平行呢?直线BD例 求证:空间四边形相邻两边中点的连线,平行于经过另外两边的平面.∵在△ABD中,E、F分别是AB、AD的中点证明:∴EF∥BD∴EF∥平面BCD 又∵ EF 平面BCD, 连接BD,三角形的中位线是常用的找平行线的方法.1.如图,四面体ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点.(3)你能说出图中满足线面平行位置关系的所有情况吗?(1)E、F、G、H四点是否共面?(2)试判断AC与平面EFGH的位置关系;练习解:(1)E、F、G、H四点共面.∵在△ABD中,E、H分别是AB、AD的中点.∴EH∥BD且同理GF∥BD且∴ EH∥GF且 EH=GF∴E、F、G、H四点共面.(2) AC ∥平面EFGH解:(3)由EF∥HG∥AC,得EF∥平面ACD,AC∥平面EFGH,HG∥平面ABC.由BD∥EH∥FG,得BD∥平面EFGH,EH∥平面BCD,FG∥平面ABD.1.如图,四面体ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点.(3)你能说出图中满足线面平行位置关系的所有情况吗?(1)E、F、G、H四点是否共面?(2)试判断AC与平面EFGH的位置关系;(1)平行(2)相交1.?平面与平面有几种位置关系?没有公共点有一条公共直线复习引入①问1:两个平面平行,那么其中一个平面的直线与另一个平面的位置关系如何?平行②问2:如果一个平面内的所有直线,都与另一个平面平行,那么这两个平面的位置关系如何?平行结论:两个平面平行的问题可以转化为一个平面内的直线与另一个平面平行的问题.③当然我们不需要证明所有直线都与另一平面平行,那么需要几条直线才能说明问题呢?复习引入2.问题:还可以怎样判定平面与平面平行呢?(两平面平行)(两平面相交)探究(两平面平行)(两平面相交)EF直线的条数不是关键!探究直线相交才是关键!探究线不在多,重在相交!2.平面与平面平行的判定定理若一个平面内两条相交直线分别平行于另一个平面, 则这两个平面平行.(1)该定理中,“两条”,“相交”都是必要条件,缺一不可: (2)该定理作用:“线面平行?面面平行”(3)应用该定理,关键是在一平面内找到两条相交直线分别与另一平面内两条直线平行即可.线线平行?线面平行?面面平行证明:因为ABCD-A1B1C1D1为正方体,
所以D1C1∥A1B1,D1C1=A1B1
又AB∥A1B1,AB=A1B1,
∴D1C1∥AB,D1C1=AB,
∴D1C1BA是平行四边形,
∴D1A∥C1B,又因为D1A 平面C1BD,CB 平面C1BD.由直线与平面平行的判定,可知同理??D1B1∥平面C1BD.
又 D1A∩D1B1=D1,所以,平面AB1D1∥平面C1BD.D1A∥平面C1BD,平行四边形对边平行是常用的找平行线的方法.练2: 正方体ABCD-A1B1C1D1中,若M、N、P、Q分别是棱A1D1,A1B1,BC,CD的中点,求证:平面AMN//平面C1QP.练1: 正方体ABCD-A1B1C1D1中,若M、N、E、F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN//平面EFDB.K变式练习证明:如图,连接BD1 ,
在△DBD1中,EF为三角形中位线,
所以EF//BD1 ,
又EF 平面ABC1D1 , BD1 平面ABC1D1
所以BD1//平面ABC1D1例 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点.求证:EF//平面ABC1D1.解:直线BD1//平面AEC,证明如下:
如图,连接BD交AC于O,再连接OE
在△DBD1中,OE为三角形中位线,
所以OE//BD1,
又BD1 平面AEC,OE 平面AEC,
故BD1//平面AEC.P56 2 如图,在长方体ABCD-A1B1C1D1中,E为DD1的中点.试判断BD1与平面AEC的位置关系,并说明理由.O注意:在直观图中,线段平行关系不变,可利用此特性先直观地找出平行线的可能所在.练习如图,已知P、Q是边长为1的正方体ABCD-A1B1C1D1的面AA1DD1 ,面ABCD的中心.求证PQ// 平面AA1B1B,并求线段的PQ长.解:(1)连接AB1,在△AB1D1中,
显然P,Q分别是AD1,D1B1的中点,
所以,PQ//AB1,且PQ= CD1
又因为PQ 平面AA1B1B
CD1 平面AA1B1B
所以 PQ// 平面AA1B1B(2)AB1 = ,PQ= 问:PQ// 平面DD1C1C?∵PQ//C1D练习C1ACB1BMNA1F证明:取A1C1中点F,连结NF,FC.∵N为A1B1中点,M是BC的中点,∴NFCM为平行四边形,故MN∥CF∴ MN∥平面AA1C1C.例 如图,三棱柱ABC-A1B1C1中,M、 N分别是BC和A1B1的中点,求证:MN∥平面AA1C1C练习练1:三棱柱ABC-A1B1C1中,E是AC1上的点,F是CB1上的中点,求证:A1B//平面ADC1 .法一:线面平行判定定理 连接BC1,则DE为△ABC1中位线, 所以EF//AB, 又EF 平面ABC ,AB 平面ABC, 故EF//平面ABC.法二:由面面平行判定线面平行 取CC1的中点G,连接GE和GF, 则GE为△ACC1中位线, 所以GE//AC, 又GE 平面ABC ,AC 平面ABC, 故GE//平面ABC.G同理可证GF//平面ABC.又GE∩GF=G,所以面GEF//面ABC.解:依题意点D为边BC的中点.
连接A1C交AC1于E,连接DE.
在△ADC1中,DE为三角形中位线,
所以DE//A1B,
又DE 平面ADC1 ,A1B 平面ADC1
故A1B//平面ADC1练2:在三棱柱ABC-A1B1C1中,△ABC为正三角形,D是BC上的点,若AD⊥BC,求证:A1B//平面ADC1 .E练习例 如图,四棱锥P-ABCD中,底面ABCD是正方形,M,N分别是AB,PC的中点,求证:MN//平面PAD.HG法二:取DC的中点G,连接GN,GM ,往证面GMN//面PAD即可.证明:取PD的中点H,连接HN,AH ,
在三角形△PDC中,HN为三角形中位线,
所以HN//DC且 HN= DC
又因为底面为正方形,且M为AB中点,
所以AM//DC且 AM= DC
∴ AM//HN且 AM=HN
即AMNH为平行四边形,故MN//AH
又AH 平面PAD ,MN 平面PAD,
故MN//平面PAD.练:如图,四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,E,F分别是PC,BD的中点,求证:EF//平面PAD.证明:分别取PD,AD的中点G,H ,连接GE,HF ,GH
在△PDC中,GE为三角形中位线,
所以GE//DC且 GE= DC
同理,HF//AB且 HF= AB
又∵底面为正方形,∴AM//DC且 AM=DC
∴ GE//HF且 GE=HF
即HFEG为平行四边形,故EF//GH
又GH 平面PAD ,EF 平面PAD,
故EF//平面PAD.GH练习例 如图,点B为△ACD所在平面外一点,M,N分别为△ABC,△ABD的重心. (1)求证:MN//平面ACD. (2)若底面边长为1为正三角形,求线段的MN的长度.解:(1)分别连接BM,BF交AC,AD于点E,F. 因为M,N分别为对应三角形的重心, 故E,F为相应边的中点,且有 BM:ME=2:1,BN:NF=2:1
∴MN//EF且MN= EF.
又因为MN 平面ACD,EF 平面ACD 所以 MN// 平面ACD.EF(2) 又因为在△ACD中,EF是三角形的中位线,
所以,EF//CD且EF= CD.
∴MN= ,CD=线段成比例也是常用的找平行线的方法.练 如图点B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD, △BCD的重心. (1)求证:平面MNG//平面ACD. (2)求 的值.EFH同理,连接BG交CD于中点H,可证NG//平面ACD且NG= FH. 又因为MN∩NG=N,所以面MNG//面ACD.练习解:(1)分别连接BM,BF交AC,AD于点E,F. 因为M,N分别为对应三角形的重心, 故E,F为相应边的中点,且有 BM:ME=2:1,BN:NF=2:1
∴MN//EF且MN= EF.
又因为MN 平面ACD,EF 平面ACD 所以 MN// 平面ACD.同理可证明NG= AC且NG//AC, MG= AD且NG//AD练 如图点B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD, △BCD的重心. (1)求证:平面MNG//平面ACD. (2)求 的值.练习解:(2)因为EF是△ACD的中位线,
所以,EF//CD且EF= CD.
由(1)知MN= EF.
∴MN= CD且MN//CD练1:如图在正方体ABCD-A1B1C1D1中,点E在AB1上,F在BD上,B1E=BF,求证:EF// 平面BB1C1C.解:(1)连接AF交BC于点K,再连接B1K,K又因为EF 平面BB1C1C
B1K 平面BB1C1C
所以EF// 平面BB1C1C练习练2:P是长方形ABCD所在平面外的一点,AB、PD两点M、N满足AM:MB=ND:NP.求证:MN∥平面PBC.练习过M作ME//AD交BD于点E,连接EN2. 线面平行判定定理应用时应注意: “面外,面内,平行”; 面面平行判定定理判定应用时应注意:“两条,相交”;小结:1.直线与平面平行的判定以及平面和平面平行的判定:3.应用判定定理判定线面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系.方法三:线段成比例.作业:P56 2+P58 1/2/3+P62 3/7/83.判断下列命题是否正确,并说明理由.
(1)若平面 内的两条直线分别与平面 平行,则
与 平行;
(2)若平面 内有无数条直线分别与平面 平行,则
与 平行;
(3)如果一个平面内任意一条直线平行于另一个平面,
那么这两个平面平行;
(4)平行于同一直线的两个平面平行;
(5)两个平面分别经过两条平行直线,这两个平面平
行;
(6)过已知平面外一条直线,必能作出与已知平面平
行的平面.×××××P58 1、3证明:假设α∩β=c. 则c∈α,c∈β
∵a∥β,a α,a与c没有交点,
又因为直线a和c共面于面α,∴而a∥c.
同理b∥c.
于是在平面α内过点P有两条相交直线与c平行,
这与平行公理矛盾,假设不成立. ∴ α ∥β.aαβcbbackback
2.2.2平面与平面平行的判定定理1.空间直线与平面的位置关系有哪几种?2.如何判定一条直线和一个平面平行呢?复习引入将课本的一边AB紧靠桌面,并绕AB转动,观察AB的对边CD在各个位置时,是不是都与桌面所在的平面平行?②从中你能得出什么结论?ABCDCD是桌面外一条直线, AB是桌面内一条直线, 若CD ∥ AB ,则CD ∥桌面.①直线AB、CD与桌面分别是什么位置关系呢?猜想:如果平面外一条直线和这个平面内的一条直线平行, 那么这条直线和这个平面平行.观察:若平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.(2)该定理作用:“线线平行?线面平行”——空间问题“平面化”即1.直线与平面平行的判定定理(1)用该定理判断直线a和平面?平行,须具备三个条件: “面外、面内、平行”(3)应用该定理,关键是在平面?内找到一条直线与已知直线a平行.已知:空间四边形ABCD中,E、F分别是AB、AD的中点.
求证:EF//平面BCD.分析: EF在面BCD外,要证明EF∥面BCD,只要证明EF和面BCD内一条直线平行即可.EF和面BCD哪一条直线平行呢?直线BD例 求证:空间四边形相邻两边中点的连线,平行于经过另外两边的平面.∵在△ABD中,E、F分别是AB、AD的中点证明:∴EF∥BD∴EF∥平面BCD 又∵ EF 平面BCD, 连接BD,三角形的中位线是常用的找平行线的方法.1.如图,四面体ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点.(3)你能说出图中满足线面平行位置关系的所有情况吗?(1)E、F、G、H四点是否共面?(2)试判断AC与平面EFGH的位置关系;练习解:(1)E、F、G、H四点共面.∵在△ABD中,E、H分别是AB、AD的中点.∴EH∥BD且同理GF∥BD且∴ EH∥GF且 EH=GF∴E、F、G、H四点共面.(2) AC ∥平面EFGH解:(3)由EF∥HG∥AC,得EF∥平面ACD,AC∥平面EFGH,HG∥平面ABC.由BD∥EH∥FG,得BD∥平面EFGH,EH∥平面BCD,FG∥平面ABD.1.如图,四面体ABCD中,E,F,G,H分别是AB,BC,CD,AD的中点.(3)你能说出图中满足线面平行位置关系的所有情况吗?(1)E、F、G、H四点是否共面?(2)试判断AC与平面EFGH的位置关系;(1)平行(2)相交1.?平面与平面有几种位置关系?没有公共点有一条公共直线复习引入①问1:两个平面平行,那么其中一个平面的直线与另一个平面的位置关系如何?平行②问2:如果一个平面内的所有直线,都与另一个平面平行,那么这两个平面的位置关系如何?平行结论:两个平面平行的问题可以转化为一个平面内的直线与另一个平面平行的问题.③当然我们不需要证明所有直线都与另一平面平行,那么需要几条直线才能说明问题呢?复习引入2.问题:还可以怎样判定平面与平面平行呢?(两平面平行)(两平面相交)探究(两平面平行)(两平面相交)EF直线的条数不是关键!探究直线相交才是关键!探究线不在多,重在相交!2.平面与平面平行的判定定理若一个平面内两条相交直线分别平行于另一个平面, 则这两个平面平行.(1)该定理中,“两条”,“相交”都是必要条件,缺一不可: (2)该定理作用:“线面平行?面面平行”(3)应用该定理,关键是在一平面内找到两条相交直线分别与另一平面内两条直线平行即可.线线平行?线面平行?面面平行证明:因为ABCD-A1B1C1D1为正方体,
所以D1C1∥A1B1,D1C1=A1B1
又AB∥A1B1,AB=A1B1,
∴D1C1∥AB,D1C1=AB,
∴D1C1BA是平行四边形,
∴D1A∥C1B,又因为D1A 平面C1BD,CB 平面C1BD.由直线与平面平行的判定,可知同理??D1B1∥平面C1BD.
又 D1A∩D1B1=D1,所以,平面AB1D1∥平面C1BD.D1A∥平面C1BD,平行四边形对边平行是常用的找平行线的方法.练2: 正方体ABCD-A1B1C1D1中,若M、N、P、Q分别是棱A1D1,A1B1,BC,CD的中点,求证:平面AMN//平面C1QP.练1: 正方体ABCD-A1B1C1D1中,若M、N、E、F分别是棱A1B1,A1D1,B1C1,C1D1的中点,求证:平面AMN//平面EFDB.K变式练习证明:如图,连接BD1 ,
在△DBD1中,EF为三角形中位线,
所以EF//BD1 ,
又EF 平面ABC1D1 , BD1 平面ABC1D1
所以BD1//平面ABC1D1例 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点.求证:EF//平面ABC1D1.解:直线BD1//平面AEC,证明如下:
如图,连接BD交AC于O,再连接OE
在△DBD1中,OE为三角形中位线,
所以OE//BD1,
又BD1 平面AEC,OE 平面AEC,
故BD1//平面AEC.P56 2 如图,在长方体ABCD-A1B1C1D1中,E为DD1的中点.试判断BD1与平面AEC的位置关系,并说明理由.O注意:在直观图中,线段平行关系不变,可利用此特性先直观地找出平行线的可能所在.练习如图,已知P、Q是边长为1的正方体ABCD-A1B1C1D1的面AA1DD1 ,面ABCD的中心.求证PQ// 平面AA1B1B,并求线段的PQ长.解:(1)连接AB1,在△AB1D1中,
显然P,Q分别是AD1,D1B1的中点,
所以,PQ//AB1,且PQ= CD1
又因为PQ 平面AA1B1B
CD1 平面AA1B1B
所以 PQ// 平面AA1B1B(2)AB1 = ,PQ= 问:PQ// 平面DD1C1C?∵PQ//C1D练习C1ACB1BMNA1F证明:取A1C1中点F,连结NF,FC.∵N为A1B1中点,M是BC的中点,∴NFCM为平行四边形,故MN∥CF∴ MN∥平面AA1C1C.例 如图,三棱柱ABC-A1B1C1中,M、 N分别是BC和A1B1的中点,求证:MN∥平面AA1C1C练习练1:三棱柱ABC-A1B1C1中,E是AC1上的点,F是CB1上的中点,求证:A1B//平面ADC1 .法一:线面平行判定定理 连接BC1,则DE为△ABC1中位线, 所以EF//AB, 又EF 平面ABC ,AB 平面ABC, 故EF//平面ABC.法二:由面面平行判定线面平行 取CC1的中点G,连接GE和GF, 则GE为△ACC1中位线, 所以GE//AC, 又GE 平面ABC ,AC 平面ABC, 故GE//平面ABC.G同理可证GF//平面ABC.又GE∩GF=G,所以面GEF//面ABC.解:依题意点D为边BC的中点.
连接A1C交AC1于E,连接DE.
在△ADC1中,DE为三角形中位线,
所以DE//A1B,
又DE 平面ADC1 ,A1B 平面ADC1
故A1B//平面ADC1练2:在三棱柱ABC-A1B1C1中,△ABC为正三角形,D是BC上的点,若AD⊥BC,求证:A1B//平面ADC1 .E练习例 如图,四棱锥P-ABCD中,底面ABCD是正方形,M,N分别是AB,PC的中点,求证:MN//平面PAD.HG法二:取DC的中点G,连接GN,GM ,往证面GMN//面PAD即可.证明:取PD的中点H,连接HN,AH ,
在三角形△PDC中,HN为三角形中位线,
所以HN//DC且 HN= DC
又因为底面为正方形,且M为AB中点,
所以AM//DC且 AM= DC
∴ AM//HN且 AM=HN
即AMNH为平行四边形,故MN//AH
又AH 平面PAD ,MN 平面PAD,
故MN//平面PAD.练:如图,四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,E,F分别是PC,BD的中点,求证:EF//平面PAD.证明:分别取PD,AD的中点G,H ,连接GE,HF ,GH
在△PDC中,GE为三角形中位线,
所以GE//DC且 GE= DC
同理,HF//AB且 HF= AB
又∵底面为正方形,∴AM//DC且 AM=DC
∴ GE//HF且 GE=HF
即HFEG为平行四边形,故EF//GH
又GH 平面PAD ,EF 平面PAD,
故EF//平面PAD.GH练习例 如图,点B为△ACD所在平面外一点,M,N分别为△ABC,△ABD的重心. (1)求证:MN//平面ACD. (2)若底面边长为1为正三角形,求线段的MN的长度.解:(1)分别连接BM,BF交AC,AD于点E,F. 因为M,N分别为对应三角形的重心, 故E,F为相应边的中点,且有 BM:ME=2:1,BN:NF=2:1
∴MN//EF且MN= EF.
又因为MN 平面ACD,EF 平面ACD 所以 MN// 平面ACD.EF(2) 又因为在△ACD中,EF是三角形的中位线,
所以,EF//CD且EF= CD.
∴MN= ,CD=线段成比例也是常用的找平行线的方法.练 如图点B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD, △BCD的重心. (1)求证:平面MNG//平面ACD. (2)求 的值.EFH同理,连接BG交CD于中点H,可证NG//平面ACD且NG= FH. 又因为MN∩NG=N,所以面MNG//面ACD.练习解:(1)分别连接BM,BF交AC,AD于点E,F. 因为M,N分别为对应三角形的重心, 故E,F为相应边的中点,且有 BM:ME=2:1,BN:NF=2:1
∴MN//EF且MN= EF.
又因为MN 平面ACD,EF 平面ACD 所以 MN// 平面ACD.同理可证明NG= AC且NG//AC, MG= AD且NG//AD练 如图点B为△ACD所在平面外一点,M,N,G分别为△ABC,△ABD, △BCD的重心. (1)求证:平面MNG//平面ACD. (2)求 的值.练习解:(2)因为EF是△ACD的中位线,
所以,EF//CD且EF= CD.
由(1)知MN= EF.
∴MN= CD且MN//CD练1:如图在正方体ABCD-A1B1C1D1中,点E在AB1上,F在BD上,B1E=BF,求证:EF// 平面BB1C1C.解:(1)连接AF交BC于点K,再连接B1K,K又因为EF 平面BB1C1C
B1K 平面BB1C1C
所以EF// 平面BB1C1C练习练2:P是长方形ABCD所在平面外的一点,AB、PD两点M、N满足AM:MB=ND:NP.求证:MN∥平面PBC.练习过M作ME//AD交BD于点E,连接EN2. 线面平行判定定理应用时应注意: “面外,面内,平行”; 面面平行判定定理判定应用时应注意:“两条,相交”;小结:1.直线与平面平行的判定以及平面和平面平行的判定:3.应用判定定理判定线面平行的关键是找平行线方法一:三角形的中位线定理;方法二:平行四边形的平行关系.方法三:线段成比例.作业:P56 2+P58 1/2/3+P62 3/7/83.判断下列命题是否正确,并说明理由.
(1)若平面 内的两条直线分别与平面 平行,则
与 平行;
(2)若平面 内有无数条直线分别与平面 平行,则
与 平行;
(3)如果一个平面内任意一条直线平行于另一个平面,
那么这两个平面平行;
(4)平行于同一直线的两个平面平行;
(5)两个平面分别经过两条平行直线,这两个平面平
行;
(6)过已知平面外一条直线,必能作出与已知平面平
行的平面.×××××P58 1、3证明:假设α∩β=c. 则c∈α,c∈β
∵a∥β,a α,a与c没有交点,
又因为直线a和c共面于面α,∴而a∥c.
同理b∥c.
于是在平面α内过点P有两条相交直线与c平行,
这与平行公理矛盾,假设不成立. ∴ α ∥β.aαβcbbackback
