高中数学必修二 第三章 小结与复习 课件 (2)
文档属性
| 名称 | 高中数学必修二 第三章 小结与复习 课件 (2) |  | |
| 格式 | zip | ||
| 文件大小 | 441.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-28 20:21:18 | ||
图片预览







文档简介
课件23张PPT。第三章《直线与方程》复习课【学习目标】
1.进一步掌握直线的倾斜角、斜率、截距等概念,直线的斜率公式.
2.掌握直线方程的几 种形式及相互转化的关系,会根据已知条件求直线方程.
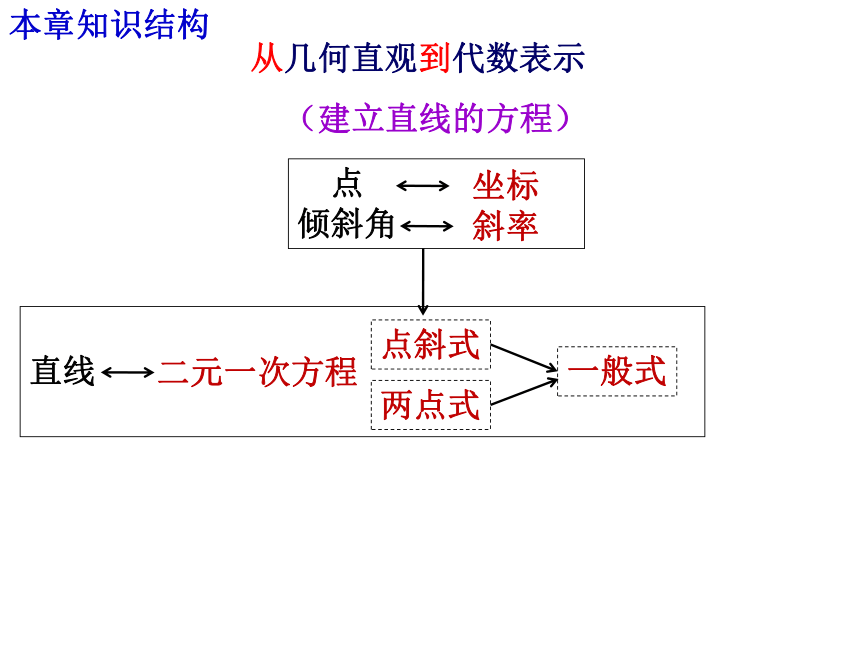
3.注意熟练地画出图形,抓住图形的特征量,利用该特征量解决问题往往能达到事半功倍的效果.本章知识结构从几何直观到代数表示 点
倾斜角
直线
点斜式两点式一般式(建立直线的方程)坐标斜率二元一次方程
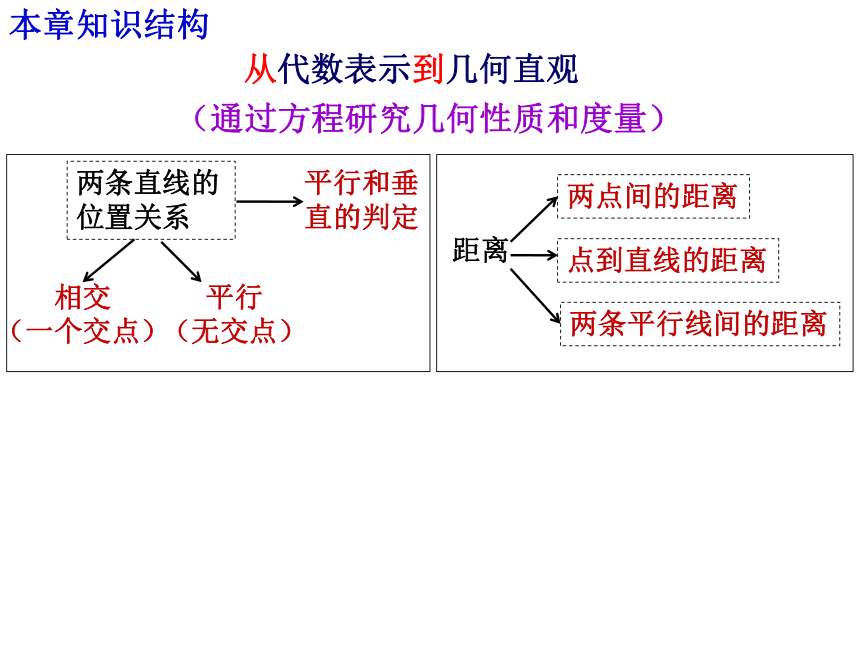
本章知识结构从代数表示到几何直观(通过方程研究几何性质和度量)两条直线的位置关系平行和垂直的判定相交
(一个交点)平行
(无交点)
距离两点间的距离点到直线的距离两条平行线间的距离【基础知识】
1.直线的倾斜角:
(1)定义:当直线l与x轴相交时,取x轴作为基准,x轴_____与直线l_________所成的角α叫做直线l的倾斜角,当直线l与x轴平行或重合时,规定它的倾斜角为____.
(2)倾斜角的取值范围:______________.
2.直线的斜率:
(1)定义: k= ( ),倾斜角是90°的直线,其斜率不存在.
(2)斜率的范围是________.
(3)斜率公式:k= .[0,π)tanα正向向上方向R90°α≠90°3、直线方程的五种形式:y-y0=k(x-x0)Ax+By+C=0
(A、B不同时为0)y=kx+b4、两直线的位置:5、距离:k1=k2且b1≠b2k1k2=-1k1≠k2k1=k2且b1=b2 A1B2-A2B1 ≠ 0A1B2-A2B1=0
B1C2-B2C1≠0(或A1C2-A2C1≠0).A1B2-A2B1=0
B1C2-B2C1=0 (且A1C2-A2C1=0)A1A2+B1B2=057x-2y-28=03x+4y-12=0-2(-1,0)【典例探究】 解法一:【典例探究】 解法二:α变式练习1:
直线l经过点A(1,2),在x轴上的截距的取值范围是(-3,3),则其斜率的取值范围是( ).例3、过点(2,1)作直线 l 分别交x,y轴正半轴于A、B两点,求当ΔAOB面积最小时,求直线 l 的方程. 例2、已知直线l 过点(1,0),且被两平行直线x+y-6=0和x+y+3=0所截得的线段长为9,求直线l的方程.【课内探究】展示与点评变式练习1:
直线l经过点A(1,2),在x轴上的截距的取值范围是(-3,3),则其斜率的取值范围是( ).A(1,2)B(-3,0)C(3,0)αβ分析:由图得D另法:设l的斜率为k,得l的点斜式方程后求出其横截距a,再由-3 和x+y+3=0所截得的线段长为9,求直线l的方程.A(1,5),B(1,-4) ,则|AB|=9.综上得,直线l方程为y=0或x=1.小结: 在求直线方程时,应先选择适当的直线方程的形式,并注意各种形式的适用条件:若采用截距式,应注意分类讨论,判断截距是否为零;若采用点斜式,应先考虑斜率不存在的情况.例3、过点(2,1)作直线 l 分别交x,y轴正半轴于A、B两点,求当ΔAOB面积最小时,求直线 l 的方程. (选做)变式练习2:
当|PA|?|PB|取最小值时,求直线 l 的方程. 解:设直线 l 的方程为 由已知 于是 当且仅当 即a=4,b=2时取等号, 此时直线l 的方程为即x+2y-4=0 解法1:设直线 l 的方程为 y-1=k(x-2)且k<0分别令y=0,x=0得当且仅当k2=1,即k=±1时取取最小值, 此时直线 l 的方程是 x+y-3=0 则|PA|?|PB|= ≥4又k<0,∴k=-1, (选做)变式练习2:
例3中,当|PA|?|PB|取最小值时,求直线 l 的方程. 例3、过点(2,1)作直线 l 分别交x,y轴正半轴于A、B两点,小结: 求直线方程最常用的方法是待定系数法.若题中直线过定点,一般设直线方程的点斜式,也可以设截距式.注意在利用基本不等式求最值时,斜率k的符号.ABθ.PEF(选做)变式练习2:
例3中,当|PA|?|PB|取最小值时,求直线 l 的方程. 例3、过点(2,1)作直线 l 分别交x,y轴正半轴于A、B两点,(选做)变式练习2:
例3中,当|PA|?|PB|取最小值时,求直线 l 的方程. 例3、过点(2,1)作直线 l 分别交x,y轴正半轴于A、B两点,1、求直线的倾斜角与斜率常运用数形结合思想.
当直线的倾斜角由锐角变到直角及由直角变到钝角时,需根据正切函数y=tan α的单调性求k的范围,数形结合是解析几何中的重要方法.【总结提升】2、求直 线方程的方法:
(1)直接法:根据已知条件,选择恰当形式的直线方程,直接求出方程中系数,写出直线方程;
(2)待定系数法:先根据已知条件设出直线方程.再根据已知条件构造关于待定系数的方程(组)求系数,最后代入求出直线方程.特别注意:求直线方程时,若不能断定直线是否具有斜率时,应对斜率存在与不存在加以讨论.在用截距式时,应先判断截距是否为0,若不确定,则需分类讨论.与直线Ax+By+C1=0平行的直线的方程可设为Ax+By+C2=0(C1≠C2)与直线Ax+By+C1=0垂直的直线的方程可设为Bx-Ay+C2=0【巩固作业】
1、必修二课本P114 B组 第1题:( ) 2、已知O(0,0)、A(8,0)、B(0,5)为矩形的三个顶点,则矩形的两条对角线所在直线的方程分别为___________________,____________________.B5x+8y-40=02.3.45x-8y=03x+2y-12=03x+2y-19=06、过点P(3,0)有一条直线l,它夹在两条直线 与 之间的线段恰被点P平分,求直线l的方程.6、已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A、B两点,求l在两轴上的截距之和最小时直线l的方程.解:(1)当直线斜率不存在时,两直线分别为x=6,x=-3此时d=9;
当直线斜率存在时,设两平行线的斜率为k,
则两直 线方程分别为 y-2=k(x-6),y+1=k(x+3),
即 kx-y-6k+2=0,kx-y+3k-1=0整理得(81-d2)k2-54k+ 9-d2=0又k∈R,则△=(-54)2-4(81-d2)(9-d2)≥0 例题4. 两条互相平行的直线分别过A(6,2)、B(–3,–1)两点的,
并且各自绕着A、B旋转,若两条平行线间距离为d.
(1) 求距离d的取值范围;
(2) 求当d取最大值时两条直线的方程.备选题解(2) 当d取最大值时,则所求直线为3x+y-20=0和3x+y+10=0例题4. 两条互相平行的直线分别过A(6,2)、B(–3,–1)两点的,
并且各自绕着A、B旋转,若两条平行线间距离为d.
(1) 求距离d的取值范围;
(2) 求当d取最大值时两条直线的方程.代入解得,k = -3.备选题
1.进一步掌握直线的倾斜角、斜率、截距等概念,直线的斜率公式.
2.掌握直线方程的几 种形式及相互转化的关系,会根据已知条件求直线方程.
3.注意熟练地画出图形,抓住图形的特征量,利用该特征量解决问题往往能达到事半功倍的效果.本章知识结构从几何直观到代数表示 点
倾斜角
直线
点斜式两点式一般式(建立直线的方程)坐标斜率二元一次方程
本章知识结构从代数表示到几何直观(通过方程研究几何性质和度量)两条直线的位置关系平行和垂直的判定相交
(一个交点)平行
(无交点)
距离两点间的距离点到直线的距离两条平行线间的距离【基础知识】
1.直线的倾斜角:
(1)定义:当直线l与x轴相交时,取x轴作为基准,x轴_____与直线l_________所成的角α叫做直线l的倾斜角,当直线l与x轴平行或重合时,规定它的倾斜角为____.
(2)倾斜角的取值范围:______________.
2.直线的斜率:
(1)定义: k= ( ),倾斜角是90°的直线,其斜率不存在.
(2)斜率的范围是________.
(3)斜率公式:k= .[0,π)tanα正向向上方向R90°α≠90°3、直线方程的五种形式:y-y0=k(x-x0)Ax+By+C=0
(A、B不同时为0)y=kx+b4、两直线的位置:5、距离:k1=k2且b1≠b2k1k2=-1k1≠k2k1=k2且b1=b2 A1B2-A2B1 ≠ 0A1B2-A2B1=0
B1C2-B2C1≠0(或A1C2-A2C1≠0).A1B2-A2B1=0
B1C2-B2C1=0 (且A1C2-A2C1=0)A1A2+B1B2=057x-2y-28=03x+4y-12=0-2(-1,0)【典例探究】 解法一:【典例探究】 解法二:α变式练习1:
直线l经过点A(1,2),在x轴上的截距的取值范围是(-3,3),则其斜率的取值范围是( ).例3、过点(2,1)作直线 l 分别交x,y轴正半轴于A、B两点,求当ΔAOB面积最小时,求直线 l 的方程. 例2、已知直线l 过点(1,0),且被两平行直线x+y-6=0和x+y+3=0所截得的线段长为9,求直线l的方程.【课内探究】展示与点评变式练习1:
直线l经过点A(1,2),在x轴上的截距的取值范围是(-3,3),则其斜率的取值范围是( ).A(1,2)B(-3,0)C(3,0)αβ分析:由图得D另法:设l的斜率为k,得l的点斜式方程后求出其横截距a,再由-3
当|PA|?|PB|取最小值时,求直线 l 的方程. 解:设直线 l 的方程为 由已知 于是 当且仅当 即a=4,b=2时取等号, 此时直线l 的方程为即x+2y-4=0 解法1:设直线 l 的方程为 y-1=k(x-2)且k<0分别令y=0,x=0得当且仅当k2=1,即k=±1时取取最小值, 此时直线 l 的方程是 x+y-3=0 则|PA|?|PB|= ≥4又k<0,∴k=-1, (选做)变式练习2:
例3中,当|PA|?|PB|取最小值时,求直线 l 的方程. 例3、过点(2,1)作直线 l 分别交x,y轴正半轴于A、B两点,小结: 求直线方程最常用的方法是待定系数法.若题中直线过定点,一般设直线方程的点斜式,也可以设截距式.注意在利用基本不等式求最值时,斜率k的符号.ABθ.PEF(选做)变式练习2:
例3中,当|PA|?|PB|取最小值时,求直线 l 的方程. 例3、过点(2,1)作直线 l 分别交x,y轴正半轴于A、B两点,(选做)变式练习2:
例3中,当|PA|?|PB|取最小值时,求直线 l 的方程. 例3、过点(2,1)作直线 l 分别交x,y轴正半轴于A、B两点,1、求直线的倾斜角与斜率常运用数形结合思想.
当直线的倾斜角由锐角变到直角及由直角变到钝角时,需根据正切函数y=tan α的单调性求k的范围,数形结合是解析几何中的重要方法.【总结提升】2、求直 线方程的方法:
(1)直接法:根据已知条件,选择恰当形式的直线方程,直接求出方程中系数,写出直线方程;
(2)待定系数法:先根据已知条件设出直线方程.再根据已知条件构造关于待定系数的方程(组)求系数,最后代入求出直线方程.特别注意:求直线方程时,若不能断定直线是否具有斜率时,应对斜率存在与不存在加以讨论.在用截距式时,应先判断截距是否为0,若不确定,则需分类讨论.与直线Ax+By+C1=0平行的直线的方程可设为Ax+By+C2=0(C1≠C2)与直线Ax+By+C1=0垂直的直线的方程可设为Bx-Ay+C2=0【巩固作业】
1、必修二课本P114 B组 第1题:( ) 2、已知O(0,0)、A(8,0)、B(0,5)为矩形的三个顶点,则矩形的两条对角线所在直线的方程分别为___________________,____________________.B5x+8y-40=02.3.45x-8y=03x+2y-12=03x+2y-19=06、过点P(3,0)有一条直线l,它夹在两条直线 与 之间的线段恰被点P平分,求直线l的方程.6、已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A、B两点,求l在两轴上的截距之和最小时直线l的方程.解:(1)当直线斜率不存在时,两直线分别为x=6,x=-3此时d=9;
当直线斜率存在时,设两平行线的斜率为k,
则两直 线方程分别为 y-2=k(x-6),y+1=k(x+3),
即 kx-y-6k+2=0,kx-y+3k-1=0整理得(81-d2)k2-54k+ 9-d2=0又k∈R,则△=(-54)2-4(81-d2)(9-d2)≥0 例题4. 两条互相平行的直线分别过A(6,2)、B(–3,–1)两点的,
并且各自绕着A、B旋转,若两条平行线间距离为d.
(1) 求距离d的取值范围;
(2) 求当d取最大值时两条直线的方程.备选题解(2) 当d取最大值时,则所求直线为3x+y-20=0和3x+y+10=0例题4. 两条互相平行的直线分别过A(6,2)、B(–3,–1)两点的,
并且各自绕着A、B旋转,若两条平行线间距离为d.
(1) 求距离d的取值范围;
(2) 求当d取最大值时两条直线的方程.代入解得,k = -3.备选题
