高中数学必修二 4.1.2圆的一般方程 课件 (2)
文档属性
| 名称 | 高中数学必修二 4.1.2圆的一般方程 课件 (2) |  | |
| 格式 | zip | ||
| 文件大小 | 174.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-28 20:19:15 | ||
图片预览






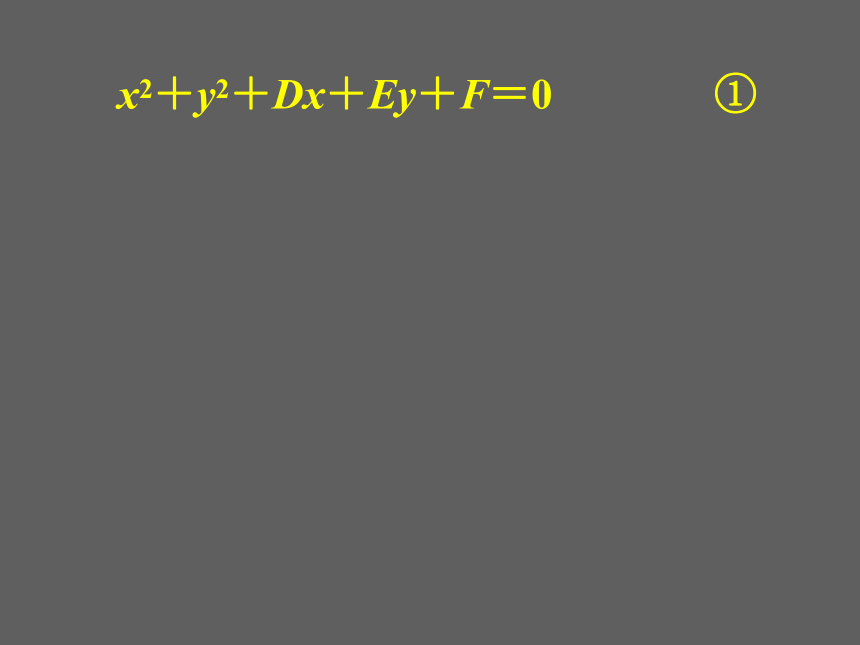
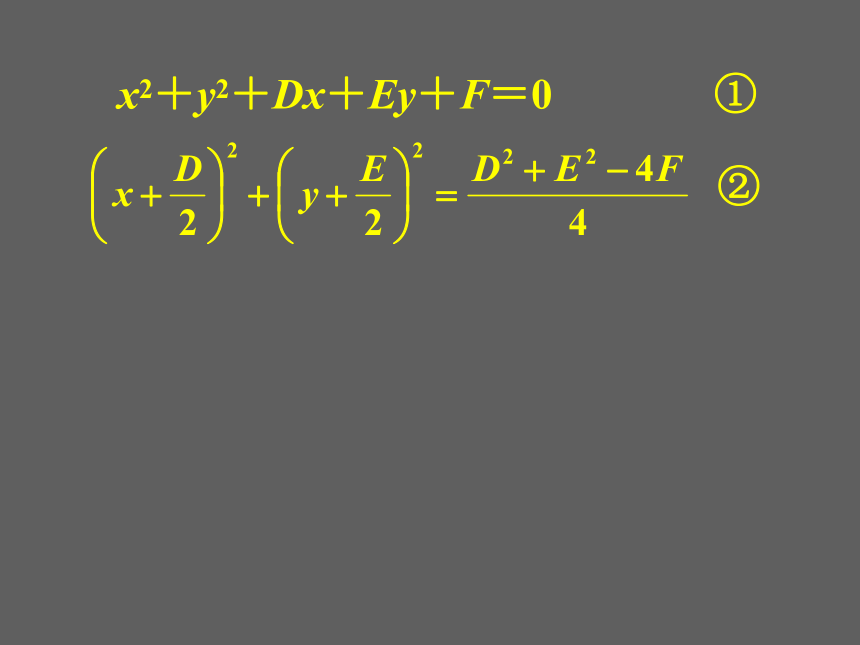

文档简介
课件28张PPT。4.1.2 圆的
一般方程复习引入圆的标准方程是什么?复习引入圆的标准方程是什么?(x-a)2+(y-b)2=r2.讲授新课对方程x2+y2-2x+4y+1=0配方,化为
圆的标准方程形式,则圆心、半径
分别是?讲授新课对方程x2+y2-2x+4y+1=0配方,化为
圆的标准方程形式,则圆心、半径
分别是?2.对方程x2+y2-2x-4y+6=0配方,能化
为圆的标准方程形式吗?讲授新课对方程x2+y2-2x+4y+1=0配方,化为
圆的标准方程形式,则圆心、半径
分别是?探究:方程x2+y2+Dx+Ey+F=0在什么
条件下表示圆?2.对方程x2+y2-2x-4y+6=0配方,能化
为圆的标准方程形式吗?x2+y2+Dx+Ey+F=0 ①②x2+y2+Dx+Ey+F=0 ①(1) 当D2+E2-4F>0时,方程①表示以②x2+y2+Dx+Ey+F=0 ①为圆心,为半径的圆.②x2+y2+Dx+Ey+F=0 ①(2) 当D2+E2-4F=0时,方程①表示点②x2+y2+Dx+Ey+F=0 ①(2) 当D2+E2-4F=0时,方程①表示点(3) 当D2+E2-4F<0时,方程①没有实数解,因而它不表示任何图形. 结 论:当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0表示一个圆,这个方程叫做圆的一般方程.例1.求过三点O(0, 0), M1(1, 1), M2(4, 2)
的圆的方程, 并求这个圆的半径长和圆
心坐标.小 结:用待定系数法求圆的方程的步骤:
小 结:用待定系数法求圆的方程的步骤:
1. 根据题意设所求圆的方程为标准式或
一般式;
小 结:用待定系数法求圆的方程的步骤:
1. 根据题意设所求圆的方程为标准式或
一般式;
2. 根据条件列出关于a、b、r或D、E、F
的方程;
小 结:用待定系数法求圆的方程的步骤:
1. 根据题意设所求圆的方程为标准式或
一般式;
2. 根据条件列出关于a、b、r或D、E、F
的方程;
3. 解方程组,求出a、b、r或D、E、F的
值,代入所设方程,就得要求的方程.例2. 圆心在直线x-y-4=0上,并且经过圆x2+y2+6x-4=0与圆x2+y2+6y-28=0的交点的圆的方程.解:因为所求圆经过两已知圆的交点,故可设其方程为:
x2+y2+6x-4+λ(x2+y2+6y-28)=0 即x^2+y^2+[6/(1+λ)]X+[6λ/(1+ λ)]y-(4+28λ)/(1+λ)=0……………………①
设圆圆心为:(-3/(1+ λ),-3λ/(1+λ))
因为圆心在直线x-y-4=0上,
故-3/(1+ λ)+3λ/(1+λ)-4=0,
解得:λ=-7 代入①可得所求圆的方程:
x^2+y^2-x+7y-32=0例3.已知线段AB的端点B的坐标是
(4, 3),端点A在圆(x+1)2 +y2=4
上运动,求线段AB的中点M的轨迹
方程.例4. 等腰三角形的顶点A的坐标是
(4, 2),底边一个端点B的坐标是
(3, 5),求另一端点C的轨迹方程,
并说明它是什么图形.例4. 等腰三角形的顶点A的坐标是
(4, 2),底边一个端点B的坐标是
(3, 5),求另一端点C的轨迹方程,
并说明它是什么图形.解:设c点坐标为(a,b) 则
(a-4)^2+(b-2)^2=(4-3)^2+(2-5)^2=10
端点C的轨迹方程以(4,2)为圆心 为半径的圆 A,B,C三点不共线,点(5,-1)除外,B点除外 例5. 长为2a的线段AB的两个端点A和B分别在x轴和y轴上滑动,求线段AB的中点的轨迹方程.例5. 长为2a的线段AB的两个端点A和B分别在x轴和y轴上滑动,求线段AB的中点的轨迹方程.解:建立直角坐标系,原点为O,A在x轴上,
B在y轴上,连接AB 设中点P的坐标为(x,y),
则A坐标为(2x,0)B坐标为(0,2y)
根据勾股定理,AO^2 + BO^2 = AB^2
就有 (2x)^2 + (2y)^2 = (2a)^2
化简得 x^2+y^2=a^2 练习1. P.123练习第3题.2. 已知一曲线是与两定点O(0, 0),A(3, 0)
的距离的比为 的点的轨迹,求这个
曲线的方程,并画出曲线课堂小结1. 圆的一般方程和标准方程;
2. 配方法和待定系数法.课后作业P124 A组 第6题 B组 第3题
一般方程复习引入圆的标准方程是什么?复习引入圆的标准方程是什么?(x-a)2+(y-b)2=r2.讲授新课对方程x2+y2-2x+4y+1=0配方,化为
圆的标准方程形式,则圆心、半径
分别是?讲授新课对方程x2+y2-2x+4y+1=0配方,化为
圆的标准方程形式,则圆心、半径
分别是?2.对方程x2+y2-2x-4y+6=0配方,能化
为圆的标准方程形式吗?讲授新课对方程x2+y2-2x+4y+1=0配方,化为
圆的标准方程形式,则圆心、半径
分别是?探究:方程x2+y2+Dx+Ey+F=0在什么
条件下表示圆?2.对方程x2+y2-2x-4y+6=0配方,能化
为圆的标准方程形式吗?x2+y2+Dx+Ey+F=0 ①②x2+y2+Dx+Ey+F=0 ①(1) 当D2+E2-4F>0时,方程①表示以②x2+y2+Dx+Ey+F=0 ①为圆心,为半径的圆.②x2+y2+Dx+Ey+F=0 ①(2) 当D2+E2-4F=0时,方程①表示点②x2+y2+Dx+Ey+F=0 ①(2) 当D2+E2-4F=0时,方程①表示点(3) 当D2+E2-4F<0时,方程①没有实数解,因而它不表示任何图形. 结 论:当D2+E2-4F>0时,方程x2+y2+Dx+Ey+F=0表示一个圆,这个方程叫做圆的一般方程.例1.求过三点O(0, 0), M1(1, 1), M2(4, 2)
的圆的方程, 并求这个圆的半径长和圆
心坐标.小 结:用待定系数法求圆的方程的步骤:
小 结:用待定系数法求圆的方程的步骤:
1. 根据题意设所求圆的方程为标准式或
一般式;
小 结:用待定系数法求圆的方程的步骤:
1. 根据题意设所求圆的方程为标准式或
一般式;
2. 根据条件列出关于a、b、r或D、E、F
的方程;
小 结:用待定系数法求圆的方程的步骤:
1. 根据题意设所求圆的方程为标准式或
一般式;
2. 根据条件列出关于a、b、r或D、E、F
的方程;
3. 解方程组,求出a、b、r或D、E、F的
值,代入所设方程,就得要求的方程.例2. 圆心在直线x-y-4=0上,并且经过圆x2+y2+6x-4=0与圆x2+y2+6y-28=0的交点的圆的方程.解:因为所求圆经过两已知圆的交点,故可设其方程为:
x2+y2+6x-4+λ(x2+y2+6y-28)=0 即x^2+y^2+[6/(1+λ)]X+[6λ/(1+ λ)]y-(4+28λ)/(1+λ)=0……………………①
设圆圆心为:(-3/(1+ λ),-3λ/(1+λ))
因为圆心在直线x-y-4=0上,
故-3/(1+ λ)+3λ/(1+λ)-4=0,
解得:λ=-7 代入①可得所求圆的方程:
x^2+y^2-x+7y-32=0例3.已知线段AB的端点B的坐标是
(4, 3),端点A在圆(x+1)2 +y2=4
上运动,求线段AB的中点M的轨迹
方程.例4. 等腰三角形的顶点A的坐标是
(4, 2),底边一个端点B的坐标是
(3, 5),求另一端点C的轨迹方程,
并说明它是什么图形.例4. 等腰三角形的顶点A的坐标是
(4, 2),底边一个端点B的坐标是
(3, 5),求另一端点C的轨迹方程,
并说明它是什么图形.解:设c点坐标为(a,b) 则
(a-4)^2+(b-2)^2=(4-3)^2+(2-5)^2=10
端点C的轨迹方程以(4,2)为圆心 为半径的圆 A,B,C三点不共线,点(5,-1)除外,B点除外 例5. 长为2a的线段AB的两个端点A和B分别在x轴和y轴上滑动,求线段AB的中点的轨迹方程.例5. 长为2a的线段AB的两个端点A和B分别在x轴和y轴上滑动,求线段AB的中点的轨迹方程.解:建立直角坐标系,原点为O,A在x轴上,
B在y轴上,连接AB 设中点P的坐标为(x,y),
则A坐标为(2x,0)B坐标为(0,2y)
根据勾股定理,AO^2 + BO^2 = AB^2
就有 (2x)^2 + (2y)^2 = (2a)^2
化简得 x^2+y^2=a^2 练习1. P.123练习第3题.2. 已知一曲线是与两定点O(0, 0),A(3, 0)
的距离的比为 的点的轨迹,求这个
曲线的方程,并画出曲线课堂小结1. 圆的一般方程和标准方程;
2. 配方法和待定系数法.课后作业P124 A组 第6题 B组 第3题
