高中数学必修二 4.2.1直线与圆的位置关系 课件 (1)
文档属性
| 名称 | 高中数学必修二 4.2.1直线与圆的位置关系 课件 (1) |

|
|
| 格式 | zip | ||
| 文件大小 | 379.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-28 00:00:00 | ||
图片预览





文档简介
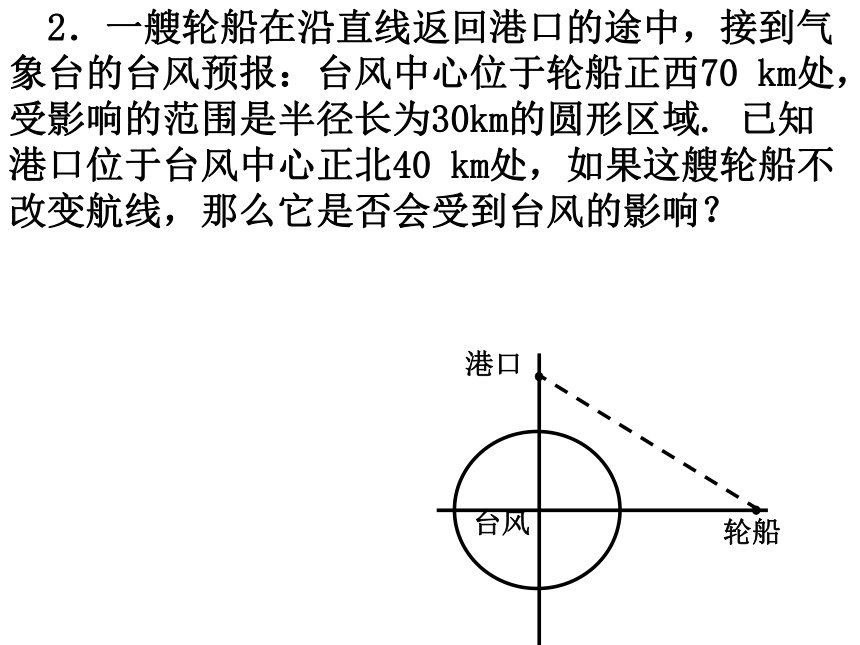
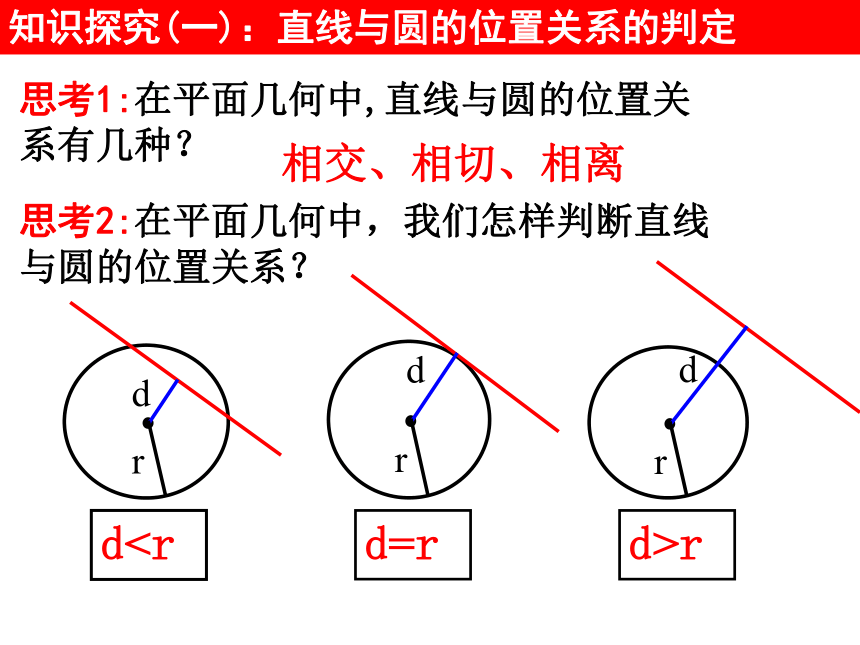
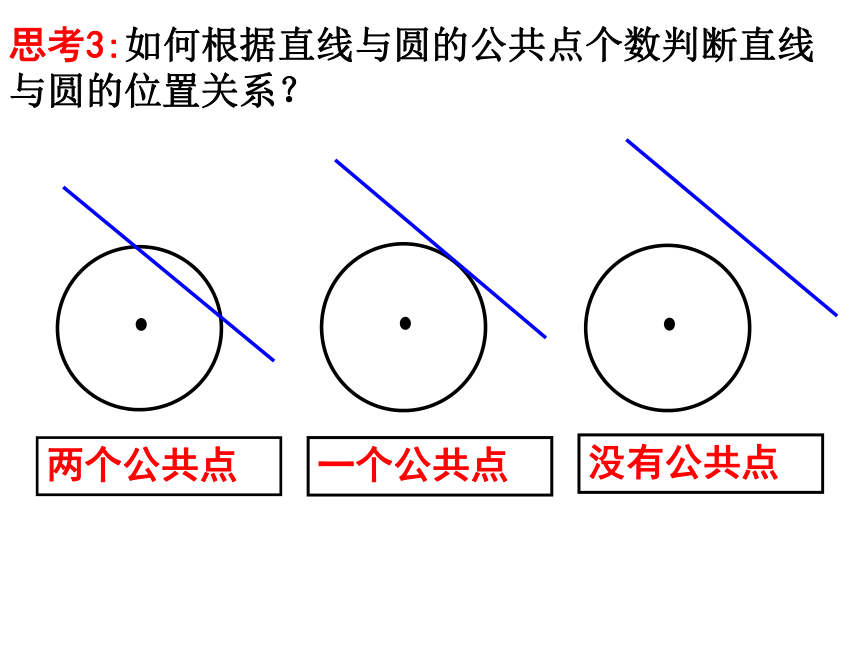
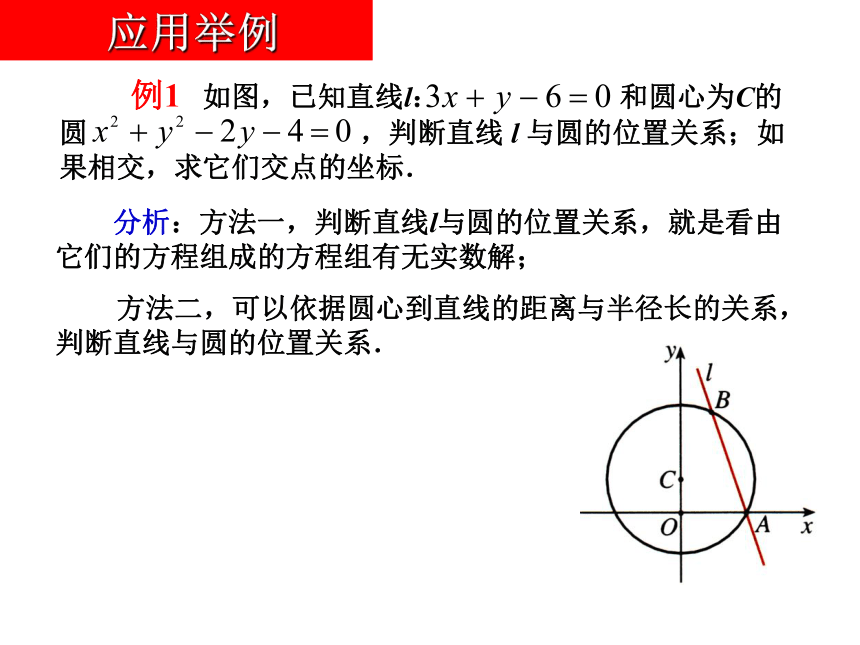
课件29张PPT。问题提出 1、点到直线的距离公式,圆的标准方程和一般方程分别是什么? 2.一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处,受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?直线与圆的位置关系知识探究(一):直线与圆的位置关系的判定 思考1:在平面几何中,直线与圆的位置关系有几种? 思考2:在平面几何中,我们怎样判断直线与圆的位置关系? dr相交、相切、相离思考3:如何根据直线与圆的公共点个数判断直线与圆的位置关系? 两个公共点一个公共点没有公共点思考4:在平面直角坐标系中,我们用方程表示直线和圆,如何根据直线与圆的方程判断它们之间的位置关系?方法一:根据直线与圆的联立方程组的公共解个数判断; 方法二:根据圆心到直线的距离与圆半径的大小关系判断.直线l:Ax+By+C=0圆C:(x-a)2+(y-b)2=r2(r>0)思考5:上述两种判断方法的操作步骤分别如何? 1.将直线方程与圆方程联立成方程组;2.通过消元,得到一个一元二次方程;3.求出其判别式△的值;4.比较△与0的大小关系:若△>0,则直线与圆相交;若△=0,则直线与圆相切;若△<0,则直线与圆相离.代数法直线与圆相离直线与圆相切直线与圆相交利用直线与圆的公共点的个数进行判断:几何法:1.把直线方程化为一般式,并求出圆心坐标和半径r;2.利用点到直线的距离公式求圆心到直线的距离d;3.利用圆心到直线的距离d与半径r的大小关系判断:直线与圆相离直线与圆相切直线与圆相交 分析:方法一,判断直线l与圆的位置关系,就是看由它们的方程组成的方程组有无实数解;
方法二,可以依据圆心到直线的距离与半径长的关系,判断直线与圆的位置关系. 例1 如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;如果相交,求它们交点的坐标. 应用举例解法一:由直线 l 与圆的方程,得:消去y,得: 例1 如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;如果相交,求它们交点的坐标. 应用举例因为:= 1 > 0所以,直线 l 与圆相交,有两个公共点. 解法二:圆 可化为其圆心C的坐标为(0,1),半径长为 ,点C (0,1)到直线 l 的距离所以,直线 l 与圆相交,有两个公共点. 例1 如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;如果相交,求它们交点的坐标. 应用举例所以,直线 l 与圆有两个交点,它们的坐标分别是:把 代入方程①,得 ;把 代入方程① ,得 . A(2,0),B(1,3)由 ,解得: 例1 如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;如果相交,求它们交点的坐标.解: 应用举例思考:怎么求弦长|AB|知识探究(二):圆的切线方程 思考1:过圆上一点、圆外一点作圆的切线,分别可作多少条? 思考2:设点M(x0,y0)为圆x2+y2=r2上一点,如何求过点M的圆的切线方程?x0x+y0y=r2思考3:设点M(x0,y0)为圆 x2+y2=r2外一点,如何求过点M的圆的切线方程?例2.已知⊙C:(x-1)2+(y-2) 2=2,P(2,-1),过P作⊙C的切线,切点为A、B。
求切线PA、PB的方程;解:解:将圆的方程写成标准形式,得:即圆心到所求直线的距离为 .如图,因为直线l 被圆所截得的弦长是 ,所以弦心距为 例3 已知过点 的直线被圆
所截得的弦长为 ,求直线的方程.因为直线l 过点 ,根据点到直线的距离公式,得到圆心到直线l 的距离:因此:所以可设所求直线l 的方程为:即:两边平方,并整理得到:解得: 所以,所求直线l有两条,它们的方程分别为:或 例3 已知过点 的直线被圆
所截得的弦长为 ,求直线的方程.解:即:变式练习1:求过点P(2,1),圆心在直线2x+y=0上,且与直线x-y-1=0相切的圆方程.Xoy 已知直线l:kx-y+6=0被圆x2+y2=25截得的弦长为8,求k值变式练习2(1) 证明:不论m取什么实数,直线 与圆恒交于两点;(2)求直线 被圆C截得弦长最小时 的方程。(1)分析:法一:△法 证: △>0法二:dr法 证:d直线 l: y=x+b, 求b的取值范围,使
(1)圆上没有一个点到直线l的距离等于1
(2)圆上恰有一个点到直线l的距离等于1
(3)圆上恰有两个点到直线l的距离等于1
(4)圆上恰有三个点到直线l的距离等于1
(5)圆上恰有四个点到直线l的距离等于1(1)当弦 长度最短时,求直线 的方程。
(2)当弦 长度最长时,求直线 的方程1、已知 内有一点 为过 的直线,交圆O于A,B两点,O课堂延伸分析:将直线平移,与圆相切的位置有两个,
这两个切点一个离直线最近,一个离直线最远最近、最远的位置找到了,又该如何求最值呢?需要将两个切点解出来吗?最大值最小值圆的标准方程为:圆心为(1,1)知识小结有无交点,有几个.直线l与圆C的方程组成的方程组是否有解,有几个解.判断圆C的圆心到直线l的距离d与圆的半径r的关系(大于、小于、等于).判断直线与圆的位置关系
方法二,可以依据圆心到直线的距离与半径长的关系,判断直线与圆的位置关系. 例1 如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;如果相交,求它们交点的坐标. 应用举例解法一:由直线 l 与圆的方程,得:消去y,得: 例1 如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;如果相交,求它们交点的坐标. 应用举例因为:= 1 > 0所以,直线 l 与圆相交,有两个公共点. 解法二:圆 可化为其圆心C的坐标为(0,1),半径长为 ,点C (0,1)到直线 l 的距离所以,直线 l 与圆相交,有两个公共点. 例1 如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;如果相交,求它们交点的坐标. 应用举例所以,直线 l 与圆有两个交点,它们的坐标分别是:把 代入方程①,得 ;把 代入方程① ,得 . A(2,0),B(1,3)由 ,解得: 例1 如图,已知直线l: 和圆心为C的圆 ,判断直线 l 与圆的位置关系;如果相交,求它们交点的坐标.解: 应用举例思考:怎么求弦长|AB|知识探究(二):圆的切线方程 思考1:过圆上一点、圆外一点作圆的切线,分别可作多少条? 思考2:设点M(x0,y0)为圆x2+y2=r2上一点,如何求过点M的圆的切线方程?x0x+y0y=r2思考3:设点M(x0,y0)为圆 x2+y2=r2外一点,如何求过点M的圆的切线方程?例2.已知⊙C:(x-1)2+(y-2) 2=2,P(2,-1),过P作⊙C的切线,切点为A、B。
求切线PA、PB的方程;解:解:将圆的方程写成标准形式,得:即圆心到所求直线的距离为 .如图,因为直线l 被圆所截得的弦长是 ,所以弦心距为 例3 已知过点 的直线被圆
所截得的弦长为 ,求直线的方程.因为直线l 过点 ,根据点到直线的距离公式,得到圆心到直线l 的距离:因此:所以可设所求直线l 的方程为:即:两边平方,并整理得到:解得: 所以,所求直线l有两条,它们的方程分别为:或 例3 已知过点 的直线被圆
所截得的弦长为 ,求直线的方程.解:即:变式练习1:求过点P(2,1),圆心在直线2x+y=0上,且与直线x-y-1=0相切的圆方程.Xoy 已知直线l:kx-y+6=0被圆x2+y2=25截得的弦长为8,求k值变式练习2(1) 证明:不论m取什么实数,直线 与圆恒交于两点;(2)求直线 被圆C截得弦长最小时 的方程。(1)分析:法一:△法 证: △>0法二:dr法 证:d
(1)圆上没有一个点到直线l的距离等于1
(2)圆上恰有一个点到直线l的距离等于1
(3)圆上恰有两个点到直线l的距离等于1
(4)圆上恰有三个点到直线l的距离等于1
(5)圆上恰有四个点到直线l的距离等于1(1)当弦 长度最短时,求直线 的方程。
(2)当弦 长度最长时,求直线 的方程1、已知 内有一点 为过 的直线,交圆O于A,B两点,O课堂延伸分析:将直线平移,与圆相切的位置有两个,
这两个切点一个离直线最近,一个离直线最远最近、最远的位置找到了,又该如何求最值呢?需要将两个切点解出来吗?最大值最小值圆的标准方程为:圆心为(1,1)知识小结有无交点,有几个.直线l与圆C的方程组成的方程组是否有解,有几个解.判断圆C的圆心到直线l的距离d与圆的半径r的关系(大于、小于、等于).判断直线与圆的位置关系
