高中数学必修二 4.2.1直线与圆的位置关系 课件 (2)
文档属性
| 名称 | 高中数学必修二 4.2.1直线与圆的位置关系 课件 (2) |

|
|
| 格式 | zip | ||
| 文件大小 | 365.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-28 00:00:00 | ||
图片预览





文档简介
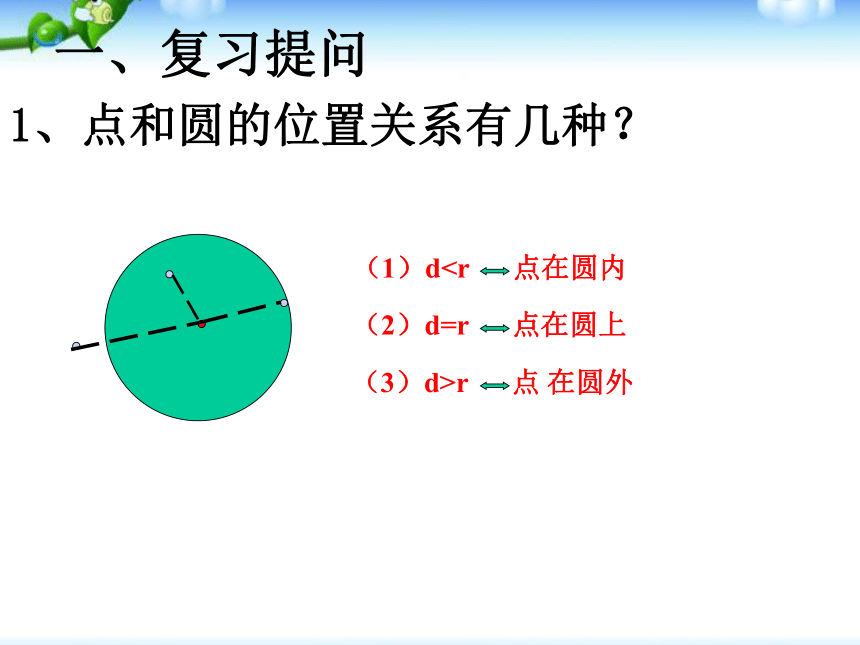
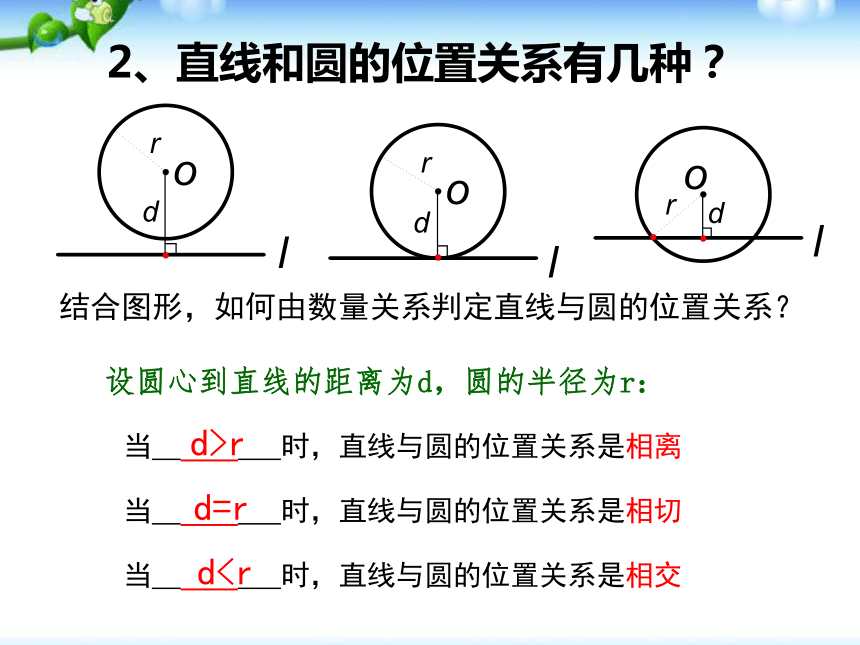
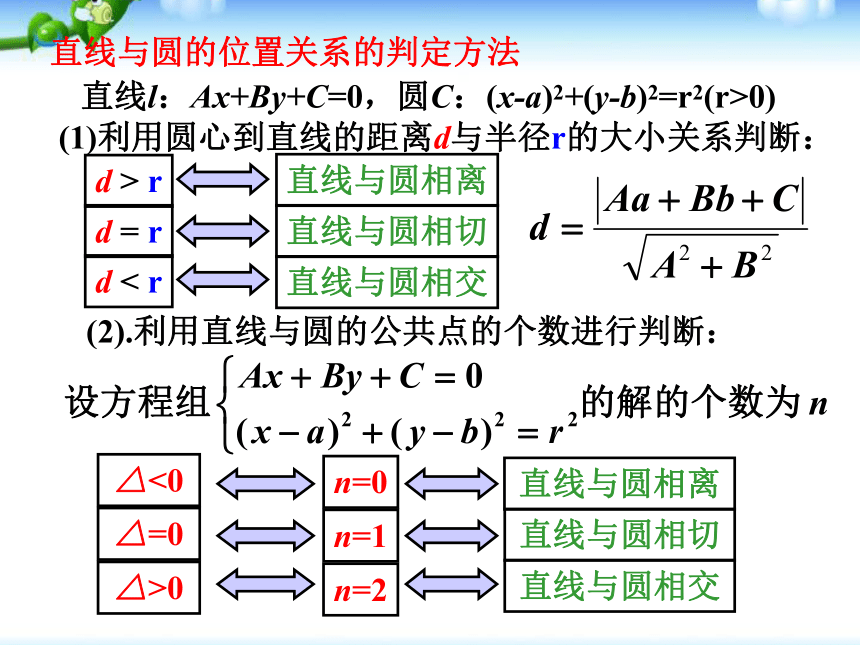
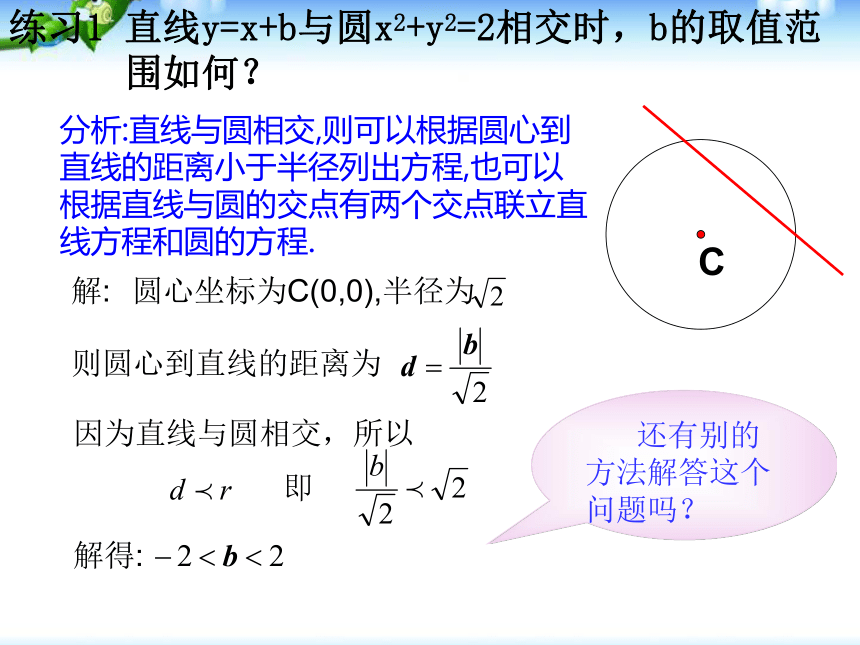
课件26张PPT。直线与圆的位置关系一、复习提问1、点和圆的位置关系有几种?结合图形,如何由数量关系判定直线与圆的位置关系?d>rd=rd0)判断下列直线与圆的位置关系相交相切相离小试身手题型一:判断直线与圆的位置关系解法一:题型一:判断直线与圆的位置关系解法二:练习1 直线y=x+b与圆x2+y2=2相交时,b的取值范
围如何? 分析:直线与圆相交,则可以根据圆心到直线的距离小于半径列出方程,也可以根据直线与圆的交点有两个交点联立直线方程和圆的方程.解:圆心坐标为C(0,0),半径为则圆心到直线的距离为因为直线与圆相交,所以即解得: 还有别的方法解答这个问题吗? 2、直线x-y-m=0与圆x2+y2=4相切时,m的取值如何? 分析:直线与圆相切,则圆心到直线的距离与圆的半径相等,即d=r。参考答案:练习1题型二 弦长问题 ( )针对性训练题型 三:直线和圆的相切问题变式测点专练( D )2.总结:判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据性质,由_________________ ______________的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r作业
1. P132 习题4.2 A组 5、6
例1 求实数m,使直线 x-my+3=0 和圆 x2+y2-6x+5=0
(1)相交;(2)相切;(3)相离。直线x-my+3=0比
较
d
与
r相交相切相离dr 例 2:已知圆 C:X2+y2=1和过点 P( -1 ,2) 的直线L.
(1)试判断点P的位置.
(2)若直线L与圆C相切 ,求直线L的方程.(3)若直线L与圆相交于A 、B两点,求直线 L
的斜率范围.(5)若直线L与圆相交于A 、B两点 ,且满足 OA⊥OB, 求直线L的方程.(4)当直线L的斜率为-1时,试判断它们的 位置关系.例3:一圆与y轴相切,圆心在直线x-3y=0上,在y=x上截得弦长为 ,求此圆的方程。解:设该圆的方程是(x-3b)2+(y-b)2=9b2, 圆心(3b,b)到直线x-y=0的距离是故所求圆的方程是(x-3)2+(y-1)2=9
或(x+3)2+(y+1)2=9。r=|3b|1.如果直线ax+by=4与圆x2+y2=4有两个不同的交点,则点P(a,b)与圆的位置关系是( )
A.P在圆外 B.P在圆上
C.P在圆内 D.不能确定
由已知,圆心(0,0)到直线ax+by=4的距离 得a2+b2>4,所以点P(a,b)在圆x2+y2=4外,选A.A2.若过原点的直线l与曲线(x-2)2+y2=1有公共点,则直线l的斜率的取值范围为( )
A.[ ]B.( )
C.[ ]D.( )
设直线方程为y=kx即y-kx=0.由题意得 解得 选C.C一、相交题型一:弦长问题为过 且倾斜角为 的弦,时,求 的长;分析:(1)已知倾斜角即知什么?已知直线上一点及斜率,怎样求直线方程?点斜式已知直线和圆的方程,如何求弦长?解 ,即半径,弦心距,半弦长构成的弦中点与圆的连线与弦垂直题型小结:(1)求圆的弦长:(2)圆的弦中点:垂直一、相交题型一:弦长问题题型二:弦中点问题(2)当弦 被点 平分时,求 的方程。为过 且倾斜角为 的弦,一、相交 (题型二:弦中点问题)二、相切题型一:求切线方程已知切线上的一个点点在圆外已知切线的斜率分析:点 是怎样的位置关系?点在圆上,即A为圆的切点法一:切线方程为:法二:圆心到切线的距离等于半径设斜率为二、相切 (题型一:求切线方程)变:想一想:法一还能用吗?为什么?不能,A点在圆外,不是切点,设切线 的斜率为圆心到切线的距离等于半径请你来找茬分析:从形的角度看:两条那为什么会漏解呢?没有讨论斜率不存在的情况错解:正解:是圆的一条切线题型小结:过一个点求圆的切线方程,应先判断点与圆的位置,若点在圆上,切线只有一条;若点在圆外,切线有两条,设切线方程时注意分斜率存在和不存在讨论,避免漏解。过圆外一点作圆的切线有几条?AC题型二:求切线长分析:已知的圆外点,圆心,切点构成用勾股定理求切线段长。题型小结:在圆中常求两种线段长:(1)相交时的弦长;(2)相切时的切线段长,都应该结合几何图形,用勾股定理求。二、相切AC二、相切 (题型二:求切线长)
围如何? 分析:直线与圆相交,则可以根据圆心到直线的距离小于半径列出方程,也可以根据直线与圆的交点有两个交点联立直线方程和圆的方程.解:圆心坐标为C(0,0),半径为则圆心到直线的距离为因为直线与圆相交,所以即解得: 还有别的方法解答这个问题吗? 2、直线x-y-m=0与圆x2+y2=4相切时,m的取值如何? 分析:直线与圆相切,则圆心到直线的距离与圆的半径相等,即d=r。参考答案:练习1题型二 弦长问题 ( )针对性训练题型 三:直线和圆的相切问题变式测点专练( D )2.总结:判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据性质,由_________________ ______________的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r作业
1. P132 习题4.2 A组 5、6
例1 求实数m,使直线 x-my+3=0 和圆 x2+y2-6x+5=0
(1)相交;(2)相切;(3)相离。直线x-my+3=0比
较
d
与
r相交相切相离d
(1)试判断点P的位置.
(2)若直线L与圆C相切 ,求直线L的方程.(3)若直线L与圆相交于A 、B两点,求直线 L
的斜率范围.(5)若直线L与圆相交于A 、B两点 ,且满足 OA⊥OB, 求直线L的方程.(4)当直线L的斜率为-1时,试判断它们的 位置关系.例3:一圆与y轴相切,圆心在直线x-3y=0上,在y=x上截得弦长为 ,求此圆的方程。解:设该圆的方程是(x-3b)2+(y-b)2=9b2, 圆心(3b,b)到直线x-y=0的距离是故所求圆的方程是(x-3)2+(y-1)2=9
或(x+3)2+(y+1)2=9。r=|3b|1.如果直线ax+by=4与圆x2+y2=4有两个不同的交点,则点P(a,b)与圆的位置关系是( )
A.P在圆外 B.P在圆上
C.P在圆内 D.不能确定
由已知,圆心(0,0)到直线ax+by=4的距离 得a2+b2>4,所以点P(a,b)在圆x2+y2=4外,选A.A2.若过原点的直线l与曲线(x-2)2+y2=1有公共点,则直线l的斜率的取值范围为( )
A.[ ]B.( )
C.[ ]D.( )
设直线方程为y=kx即y-kx=0.由题意得 解得 选C.C一、相交题型一:弦长问题为过 且倾斜角为 的弦,时,求 的长;分析:(1)已知倾斜角即知什么?已知直线上一点及斜率,怎样求直线方程?点斜式已知直线和圆的方程,如何求弦长?解 ,即半径,弦心距,半弦长构成的弦中点与圆的连线与弦垂直题型小结:(1)求圆的弦长:(2)圆的弦中点:垂直一、相交题型一:弦长问题题型二:弦中点问题(2)当弦 被点 平分时,求 的方程。为过 且倾斜角为 的弦,一、相交 (题型二:弦中点问题)二、相切题型一:求切线方程已知切线上的一个点点在圆外已知切线的斜率分析:点 是怎样的位置关系?点在圆上,即A为圆的切点法一:切线方程为:法二:圆心到切线的距离等于半径设斜率为二、相切 (题型一:求切线方程)变:想一想:法一还能用吗?为什么?不能,A点在圆外,不是切点,设切线 的斜率为圆心到切线的距离等于半径请你来找茬分析:从形的角度看:两条那为什么会漏解呢?没有讨论斜率不存在的情况错解:正解:是圆的一条切线题型小结:过一个点求圆的切线方程,应先判断点与圆的位置,若点在圆上,切线只有一条;若点在圆外,切线有两条,设切线方程时注意分斜率存在和不存在讨论,避免漏解。过圆外一点作圆的切线有几条?AC题型二:求切线长分析:已知的圆外点,圆心,切点构成用勾股定理求切线段长。题型小结:在圆中常求两种线段长:(1)相交时的弦长;(2)相切时的切线段长,都应该结合几何图形,用勾股定理求。二、相切AC二、相切 (题型二:求切线长)
