高中数学必修二 第四章小结与复习 课件 (1)
文档属性
| 名称 | 高中数学必修二 第四章小结与复习 课件 (1) |

|
|
| 格式 | zip | ||
| 文件大小 | 164.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-28 00:00:00 | ||
图片预览











文档简介
课件113张PPT。
第四章 圆与方程
4.1 圆的方程4.1.1 圆的标准方程问题提出1.在平面直角坐标系中,两点确定一条
直线,一点和倾斜角也确定一条直线,
那么在什么条件下可以确定一个圆呢?2.直线可以用一个方程表示,圆也可以用一个方程来表示,怎样建立圆的方程是我们需要探究的问题. 圆心和半径圆的标准方程知识探究一:圆的标准方程 平面上到一个定点的距离等于定长的点的轨迹叫做圆. P={M||MA|=r}.思考2:确定一个圆最基本的要素是什么?思考3:设圆心坐标为A(a,b),圆半径
为r,M(x,y)为圆上任意一点,根据圆的定义x,y应满足什么关系?(x-a)2+(y-b)2=r2思考4:对于以点A(a,b)为圆心,r为半径的圆,由上可知,若点M(x,y)在圆上,则点M的坐标满足方程(x-a)2+(y-b)2=r2 ;反之,若点M(x,y)的坐标适合方程(x-a)2+(y-b)2=r2 ,那么点M一定在这个圆上吗?思考6:以原点为圆心,1为半径的圆称为单位圆,那么单位圆的方程是什么?思考5:我们把方程 称为圆心为A(a,b),半径长为r的圆的标准方程,那么确定圆的标准方程需要几个独立条件?x2+y2=r2思考7:方程 ,
,
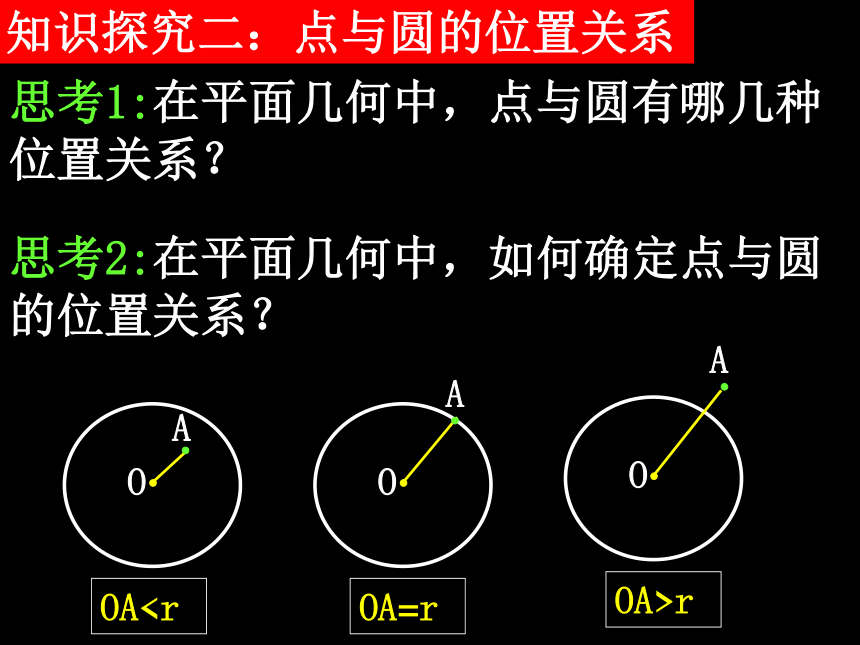
是圆方程吗?知识探究二:点与圆的位置关系 思考1:在平面几何中,点与圆有哪几种位置关系? OArOA=r思考3:在直角坐标系中,已知点M(x0,y0)和圆C: ,如何判断点M在圆外、圆上、圆内?(x0-a)2+(y0-b)2>r2时,点M在圆C外;(x0-a)2+(y0-b)2=r2时,点M在圆C上;(x0-a)2+(y0-b)2表示的图形是什么? 理论迁移 例1 写出圆心为A(2,-3),半径长等于5的圆的方程,并判断点M(5, -7),N( ,-1)是否在这个圆上? 例2 △ABC的三个顶点的坐标分别是 A(5,1),B(7,-3),C(2,-8),求它的外接圆的方程. 例3 已知圆心为C的圆经过点 A(1,1)和B(2,-2),且圆心C在 直线l :x-y+1=0上,求圆C的标准方程.(1)圆的标准方程的结构特点.(2)点与圆的位置关系的判定.(3)求圆的标准方程的方法:
①待定系数法;②代入法.小结作业作业:
P120练习: 1,3.
P124习题4.1A组:2,3,4. 4.1.2 圆的一般方程问题提出 1.圆心为A(a,b),半径为r的圆的标准方程是什么? 2.直线方程有多种形式,圆的方程是否还可以表示成其他形式?这是一个需要探讨的问题. 圆的一般方程知识探究一:圆的一般方程 思考1:圆的标准方程
展开可得到一个什么式子?思考2:方程
的一般形式是什么?思考3:方程
与 表示的图形都是圆吗?为什么?思考4:方程 可化
为 ,
它在什么条件下表示圆?思考5:当 或 时,方程 表示什么图形?圆心为 ,半径为 思考7:当D=0,E=0或F=0时,
圆 的位置分别有什么特点? D=0E=0F=0知识探究二:圆的直径方程 思考1:已知点A(1,3)和B(-5,5),如何求以线段AB为直径的圆方程? 思考2:一般地,已知点A(x1,y1),B(x2,y2),则以线段AB为直径的圆方程如何? (x-x1)(x-x2)+(y-y1)(y-y2)=0理论迁移 例1 求过三点O(0,0),A(1,1),B(4,2)的圆的方程,并求出这个圆的半径长和圆心坐标.例2 方程
表示的图形是一个圆,求a的取值范围.例3 已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程. 例4 已知点P(5,3),点M在圆x2+y2-4x+2y+4=0上运动,求|PM|的最大值和最小值.1.任一圆的方程可写成 的形式,但方程 表示的曲线不一定是圆,当 时,方程表示圆心为 ,半径
为 的圆.小结作业2.用待定系数法求圆方程的基本步骤:
(1)设圆方程 ;(2)列方程组;
(3)求系数; (4)小结. 3.求轨迹方程的基本思想:
求出动点坐标x,y所满足的关系.作业:
P123练习:1,2,3.
P124习题4.1B组:1,2,3.4.2 直线、圆的位置关系4.2.1 直线与圆的位置关系问题提出 1、点到直线的距离公式, 圆的标准方程和一般方程分别是什么? 2.一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处,受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?直线与圆的位置关系知识探究(一):直线与圆的位置关系的判定 思考1:在平面几何中,直线与圆的位置关系有几种? 思考2:在平面几何中,我们怎样判断直线与圆的位置关系? dr思考3:如何根据直线与圆的公共点个数判断直线与圆的位置关系? 两个公共点一个公共点没有公共点思考4:在平面直角坐标系中,我们用方程表示直线和圆,如何根据直线与圆的方程判断它们之间的位置关系?方法一:根据直线与圆的联立方程组的公共解个数判断; 方法二:根据圆心到直线的距离与圆半径的大小关系判断.思考5:上述两种判断方法的操作步骤分别如何? 代数法:1.将直线方程与圆方程联立成方程组;2.通过消元,得到一个一元二次方程;3.求出其判别式△的值;4.比较△与0的大小关系:若△>0,则直线与圆相交;若△=0,则直线与圆相切;若△<0,则直线与圆相离.几何法:1.把直线方程化为一般式,并求出圆心坐标和半径r;2.利用点到直线的距离公式求圆心到直线的距离d;若d>r,则直线与圆相离;
若d=r,则直线与圆相切;
若d<r,则直线与圆相交.3.比较d与r的大小关系:知识探究(二):圆的切线方程 思考1:过圆上一点、圆外一点作圆的切线,分别可作多少条? 思考2:设点M(x0,y0)为圆x2+y2=r2上一点,如何求过点M的圆的切线方程?x0x+y0y=r2思考3:设点M(x0,y0)为圆 x2+y2=r2外一点,如何求过点M的圆的切线方程?思考4:设点M(x0,y0)为圆x2+y2=r2外一点,过点M作圆的两条切线,切点分别为A,B,则直线AB的方程如何? x0x+y0y=r2理论迁移 例1 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求两个交点的距离. 例2 过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为 ,求直线l的方程. 例3 求过点P(2,1),圆心在直线2x+y=0上,且与直线x-y-1=0相切的圆方程.
作业:
P128练习:2,3,4.
P132习题4.2A组:2,3,5.4.2.2 圆与圆的位置关系问题提出 1.点与圆、直线与圆的位置关系有哪几种?如何判定这些位置关系? 2.圆与圆的位置关系有哪几种?如何根据圆的方程判断圆与圆的位置关系,我们将进一步探究.圆与圆的位置关系知识探究(一):圆与圆的位置关系思考1:两个大小不等的圆,其位置关系有内含、内切、相交、外切、外离等五种,在平面几何中,这些位置关系是如何判定的? 思考2:已知两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0,用上述方法判断两个圆位置关系的操作步骤如何? 1.将两圆的方程化为标准方程;2.求两圆的圆心坐标和半径R、r;3.求两圆的圆心距d; 4.比较d与R-r,R+r的大小关系:思考4:两个大小相等的圆的位置关系有哪几种? 思考3:能否根据两个圆的公共点个数判断两圆的位置关系? 若d<|R-r|,则两圆内含; 若d=|R-r|,则两圆内切; 若|R-r|<d<R+r,则两圆相交;若d=R+r,则两圆外切; 若d>R+r,则两圆外离. 知识探究(二):相交圆的交线方程 思考1:已知两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0, 则方程
x2+y2+D1x+E1y+F1-(x2+y2+D2x+E2y+F2)=0表示的图形是什么?思考2:若两圆 C1:x2+y2+D1x+E1y+F1=0 和 C2:x2+y2+D2x+E2y+F2=0相交, M(x0,y0)为一个交点, 则点M(x0,y0)在直线
(D1-D2)x+(E1-E2)y+F1-F2=0上吗? 思考3:若两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0相交, 则其公共弦所在直线的方程是 (D1-D2)x+(E1-E2)y+F1-F2=0,那么过交点的圆系方程是什么? m(x2+y2+D1x+E1y+F1)+n(x2+y2+D2x+E2y+F2)=0 思考4:若两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0相切, 则方程
(D1-D2)x+(E1-E2)y+F1-F2=0表示的直线是什么?若两圆相离呢?理论迁移 例1 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,判断圆C1与圆C2的位置关系. 若相交,求两圆的公共弦所在的直线方程. x2+y2-6x-4=0 x2+y2-4x-2y-1=0 例2 已知一个圆的圆心为M(2,1),且与圆C:x2+y2-3x=0相交于A、B两点,若圆心M到直线AB的距离为 ,求圆M的方程. 作业:
P132习题4.2A组:4,6,9,10.4.2.3 直线与圆的方程的应用问题提出 通过直线与圆的方程,可以确定直线与圆、圆和圆的位置关系,对于生产、生活实践以及平面几何中与直线和圆有关的问题,我们可以建立直角坐标系,通过直线与圆的方程,将其转化为代数问题来解决.对此,我们必须掌握解决问题的基本思想和方法.直线与圆
的方程的应用知识探究:直线与圆的方程在实际生活中的应用 问题Ⅰ:一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?思考1:解决这个问题的本质是什么?思考2:你有什么办法判断轮船航线是否经过台风圆域?思考3:如图所示建立直角坐标系,取10km为长度单位,那么轮船航线所在直线和台风圆域边界所在圆的方程分别是什么?思考4:直线4x+7y-28=0与圆x2+y2=9的位置关系如何?对问题Ⅰ应作怎样的回答?问题Ⅱ:如图是某圆拱形桥一孔圆拱的示意图. 这个圆的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m)思考1:你能用几何法求支柱A2P2的高度吗?思考2:如图所示建立直角坐标系,那么求支柱A2P2的高度,化归为求一个什么问题?思考4:利用这个圆的方程可求得点P2的纵坐标是多少?问题Ⅱ的答案如何?思考3:取1m为长度单位,如何求圆拱所在圆的方程?x2+(y+10.5)2=14.52 知识探究:直线与圆的方程在平面几何中的应用 问题Ⅱ:已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.思考1:许多平面几何问题常利用“坐标法”来解决,首先要做的工作是建立适当的直角坐标系,在本题中应如何选取坐标系?思考2:如图所示建立直角坐标系,设四边形的四个顶点分别为点 A(a,0),B(0,b),C(c,0), D(0,d),那么BC边的长为多少?思考3:四边形ABCD的外接圆圆心M的坐标如何?思考4:如何计算圆心M到直线AD的距离|MN|?思考5:由上述计算可得|BC|=2|MN|,从而命题成立.你能用平面几何知识证明这个命题吗?理论迁移 例1 如图,在Rt△AOB中,|OA|=4,|OB|=3,∠AOB=90°,点P是△AOB内切圆上任意一点,求点P到顶点A、O、B的距离的平方和的最大值和最小值. 例2 如图,圆O1和圆O2的半径都等于1,圆心距为4,过动点P分别作圆O1和圆O2的切线,切点为M、N,且使得|PM|= |PN|,试求点P的运动轨迹是什么曲线?
作业:
P132练习:1,2,3,4.
P133习题4.2B组:1,2,3. 4.3 空间直角坐标系 4.3.1 空间直角坐标系 问题提出 对于直线上的点,我们可以通过数轴来确定点的位置;对于平面上的点,我们可以通过平面直角坐标系来确定点的位置;对于空间中的点,我们也希望建立适当的坐标系来确定点的位置. 因此,如何在空间中建立坐标系,就成为我们需要研究的课题.空间直角坐标系知识探究(一):空间直角坐标系 思考1:数轴上的点M的坐标用一个实数x表示,它是一维坐标;平面上的点M的坐标用一对有序实数(x,y)表示,它是二维坐标.设想:对于空间中的点的坐标,需要几个实数表示?思考2:平面直角坐标系由两条互相垂直的数轴组成,设想:空间直角坐标系由几条数轴组成?其相对位置关系如何? 三条交于一点且两两互相垂直的数轴 思考3:在空间中,取三条交于一点且两两互相垂直的数轴:x轴、y轴、z轴,组成空间直角坐标系Oxyz,在平面上如何画空间直角坐标系? ∠xOy=135°∠yOz=90° 思考4:在空间直角坐标系中,对三条数轴的方向作如下约定:伸出右手,拇指指向为x轴正方向,食指指向为y轴正方向,中指指向为z轴正方向,并称这样的坐标系为右手直角坐标系.那么下列空间直角坐标系中哪些是右手直角坐标系?思考5:在空间直角坐标系Oxyz中,其中点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,通过每两个坐标轴的平面叫做坐标平面,并分别称为xOy平面、yOz平面、xOz平面.这三个坐标平面的位置关系如何?思考6:如图,在长方体ABCD-A1B1C1D1中,以点D为坐标原点建立空间右手直角坐标系,那么x轴、y轴、z轴
应如何选取?思考7:在空间直角坐标系Oxyz中,三个坐标平面将空间分成几个部分?知识探究(二)空间直角坐标系中点的坐标 思考1:在平面直角坐标系中,点M的横坐标、纵坐标的含义如何? 思考2:在空间直角坐标系中,设点M为空间的一个定点,过点M分别作垂直于x轴、y轴、z轴的平面,垂足为A、B、C. 设点A、B、C在x轴、y轴、z轴上的坐标分别为x、y、z,那么点M的位置与有序实数组(x,y,z)是一个什么对应关系? 思考3:上述有序实数组(x,y,z)称为点M的空间坐标,其中x、y、z分别叫做点M的横坐标、纵坐标、
竖坐标,这三个坐标的值一定是正数吗?xyz思考4:x轴、y轴、z轴上的点的坐标有何特点?xOy平面、yOz平面、xOz平面上的点的坐标有何特点?x轴上的点:(x,0,0)xOy平面上的点:(x,y,0)思考5:设点M的坐标为(a,b,c)过点M分别作xOy平面、yOz平面、xOz平面的垂线,那么三个垂足的坐标分别如何?A(a,b,0)B(0,b,c)C(a,0,c)思考6:设点M的坐标为(x,y,z)那么点M关于x轴、y轴、z轴及原点对称的点的坐标分别是什么?M(x,y,z)N(x,-y,-z)思考7:设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?理论迁移 例1 如图,在长方体OABC-D′A′B′C′中,|OA|=3,|OC|=4,
|OD′|=2,写出长方体各顶点的坐标. 例2 结晶体的基本单位称为晶胞,下图是食盐晶胞的示意图(可看成是八个棱长为0.5的小正方体堆积成的正方体),其中色点代表钠原子,白点代表氯原子.如图建立直角坐标系Oxyz,试写出全部钠原子所在位置的坐标.作业:
P136练习:1,2,3.
P138习题4.3A组:2. 4.3.2 空间两点间的距离公式 问题提出 1. 在平面直角坐标系中两点间的距离公式是什么? 2. 在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.空间两点间的距离公式知识探究(一):与坐标原点的距离公式 思考1:在空间直角坐标系中,坐标轴上的点A(x,0,0),B(0,y,0),C(0,0,z),与坐标原点O的距离分别是什么?|OA|=|x||OB|=|y||OC|=|z|思考2:在空间直角坐标系中,坐标平面上的点A(x,y,0),B(0,y,z),C(x,0,z),与坐标原点O的距离分别是什么?思考3:在空间直角坐标系中,设点 P(x,y,z)在xOy平面上的射影为M,则点M的坐标是什么?|PM|,|OM|的值分别是什么?M(x,y,0)|PM|=|z|思考4:基于上述分析,你能得到点 P(x,y,z)与坐标原点O的距离公式吗?思考5:在空间直角坐标系中,方程 x2+y2+z2=r2(r>0为常数)表示什么图形是什么? 知识探究(二):空间两点间的距离公式 在空间中,设点P1(x1,y1,z1),P2(x2,y2,z2)在xOy平面上的射影分别为M、N.思考1:点M、N之间的距离如何?思考2:若直线P1P2垂直于xOy平面,则点P1、P2之间的距离如何?|P1P2|=|z1-z2|思考3:若直线P1P2平行于xOy平面,则点P1、P2之间的距离如何?思考4:若直线P1P2 是xOy平面的一条斜线,则点P1、P2的距离如何计算?思考5:在上述图形背景下,点P1(x1,y1,z1)与P2(x2,y2,z2)之间的距离是
它对任意两点P1、P2都成立吗? 例1 在空间中,已知点A(1, 0, -1),B (4, 3, -1),求A、B两点之间的距离.理论迁移 例2 已知两点 A(-4, 1, 7)和B(3, 5, -2),点P在z轴上,若|PA|=|PB|,求点P的坐标. 例3 如图,点P、Q分别在棱长为1的正方体的对角线AB和棱CD上运动,求P、Q两点间的距离的最小值,并指出此时P、Q两点的位置. 作业:
P138练习:1,2,3,4.
第四章 圆与方程
4.1 圆的方程4.1.1 圆的标准方程问题提出1.在平面直角坐标系中,两点确定一条
直线,一点和倾斜角也确定一条直线,
那么在什么条件下可以确定一个圆呢?2.直线可以用一个方程表示,圆也可以用一个方程来表示,怎样建立圆的方程是我们需要探究的问题. 圆心和半径圆的标准方程知识探究一:圆的标准方程 平面上到一个定点的距离等于定长的点的轨迹叫做圆. P={M||MA|=r}.思考2:确定一个圆最基本的要素是什么?思考3:设圆心坐标为A(a,b),圆半径
为r,M(x,y)为圆上任意一点,根据圆的定义x,y应满足什么关系?(x-a)2+(y-b)2=r2思考4:对于以点A(a,b)为圆心,r为半径的圆,由上可知,若点M(x,y)在圆上,则点M的坐标满足方程(x-a)2+(y-b)2=r2 ;反之,若点M(x,y)的坐标适合方程(x-a)2+(y-b)2=r2 ,那么点M一定在这个圆上吗?思考6:以原点为圆心,1为半径的圆称为单位圆,那么单位圆的方程是什么?思考5:我们把方程 称为圆心为A(a,b),半径长为r的圆的标准方程,那么确定圆的标准方程需要几个独立条件?x2+y2=r2思考7:方程 ,
,
是圆方程吗?知识探究二:点与圆的位置关系 思考1:在平面几何中,点与圆有哪几种位置关系? OA
①待定系数法;②代入法.小结作业作业:
P120练习: 1,3.
P124习题4.1A组:2,3,4. 4.1.2 圆的一般方程问题提出 1.圆心为A(a,b),半径为r的圆的标准方程是什么? 2.直线方程有多种形式,圆的方程是否还可以表示成其他形式?这是一个需要探讨的问题. 圆的一般方程知识探究一:圆的一般方程 思考1:圆的标准方程
展开可得到一个什么式子?思考2:方程
的一般形式是什么?思考3:方程
与 表示的图形都是圆吗?为什么?思考4:方程 可化
为 ,
它在什么条件下表示圆?思考5:当 或 时,方程 表示什么图形?圆心为 ,半径为 思考7:当D=0,E=0或F=0时,
圆 的位置分别有什么特点? D=0E=0F=0知识探究二:圆的直径方程 思考1:已知点A(1,3)和B(-5,5),如何求以线段AB为直径的圆方程? 思考2:一般地,已知点A(x1,y1),B(x2,y2),则以线段AB为直径的圆方程如何? (x-x1)(x-x2)+(y-y1)(y-y2)=0理论迁移 例1 求过三点O(0,0),A(1,1),B(4,2)的圆的方程,并求出这个圆的半径长和圆心坐标.例2 方程
表示的图形是一个圆,求a的取值范围.例3 已知线段AB的端点B的坐标是(4,3),端点A在圆(x+1)2+y2=4上运动,求线段AB的中点M的轨迹方程. 例4 已知点P(5,3),点M在圆x2+y2-4x+2y+4=0上运动,求|PM|的最大值和最小值.1.任一圆的方程可写成 的形式,但方程 表示的曲线不一定是圆,当 时,方程表示圆心为 ,半径
为 的圆.小结作业2.用待定系数法求圆方程的基本步骤:
(1)设圆方程 ;(2)列方程组;
(3)求系数; (4)小结. 3.求轨迹方程的基本思想:
求出动点坐标x,y所满足的关系.作业:
P123练习:1,2,3.
P124习题4.1B组:1,2,3.4.2 直线、圆的位置关系4.2.1 直线与圆的位置关系问题提出 1、点到直线的距离公式, 圆的标准方程和一般方程分别是什么? 2.一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处,受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?直线与圆的位置关系知识探究(一):直线与圆的位置关系的判定 思考1:在平面几何中,直线与圆的位置关系有几种? 思考2:在平面几何中,我们怎样判断直线与圆的位置关系? d
若d=r,则直线与圆相切;
若d<r,则直线与圆相交.3.比较d与r的大小关系:知识探究(二):圆的切线方程 思考1:过圆上一点、圆外一点作圆的切线,分别可作多少条? 思考2:设点M(x0,y0)为圆x2+y2=r2上一点,如何求过点M的圆的切线方程?x0x+y0y=r2思考3:设点M(x0,y0)为圆 x2+y2=r2外一点,如何求过点M的圆的切线方程?思考4:设点M(x0,y0)为圆x2+y2=r2外一点,过点M作圆的两条切线,切点分别为A,B,则直线AB的方程如何? x0x+y0y=r2理论迁移 例1 已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求两个交点的距离. 例2 过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为 ,求直线l的方程. 例3 求过点P(2,1),圆心在直线2x+y=0上,且与直线x-y-1=0相切的圆方程.
作业:
P128练习:2,3,4.
P132习题4.2A组:2,3,5.4.2.2 圆与圆的位置关系问题提出 1.点与圆、直线与圆的位置关系有哪几种?如何判定这些位置关系? 2.圆与圆的位置关系有哪几种?如何根据圆的方程判断圆与圆的位置关系,我们将进一步探究.圆与圆的位置关系知识探究(一):圆与圆的位置关系思考1:两个大小不等的圆,其位置关系有内含、内切、相交、外切、外离等五种,在平面几何中,这些位置关系是如何判定的? 思考2:已知两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0,用上述方法判断两个圆位置关系的操作步骤如何? 1.将两圆的方程化为标准方程;2.求两圆的圆心坐标和半径R、r;3.求两圆的圆心距d; 4.比较d与R-r,R+r的大小关系:思考4:两个大小相等的圆的位置关系有哪几种? 思考3:能否根据两个圆的公共点个数判断两圆的位置关系? 若d<|R-r|,则两圆内含; 若d=|R-r|,则两圆内切; 若|R-r|<d<R+r,则两圆相交;若d=R+r,则两圆外切; 若d>R+r,则两圆外离. 知识探究(二):相交圆的交线方程 思考1:已知两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0, 则方程
x2+y2+D1x+E1y+F1-(x2+y2+D2x+E2y+F2)=0表示的图形是什么?思考2:若两圆 C1:x2+y2+D1x+E1y+F1=0 和 C2:x2+y2+D2x+E2y+F2=0相交, M(x0,y0)为一个交点, 则点M(x0,y0)在直线
(D1-D2)x+(E1-E2)y+F1-F2=0上吗? 思考3:若两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0相交, 则其公共弦所在直线的方程是 (D1-D2)x+(E1-E2)y+F1-F2=0,那么过交点的圆系方程是什么? m(x2+y2+D1x+E1y+F1)+n(x2+y2+D2x+E2y+F2)=0 思考4:若两圆 C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0相切, 则方程
(D1-D2)x+(E1-E2)y+F1-F2=0表示的直线是什么?若两圆相离呢?理论迁移 例1 已知圆C1:x2+y2+2x+8y-8=0,圆C2:x2+y2-4x-4y-2=0,判断圆C1与圆C2的位置关系. 若相交,求两圆的公共弦所在的直线方程. x2+y2-6x-4=0 x2+y2-4x-2y-1=0 例2 已知一个圆的圆心为M(2,1),且与圆C:x2+y2-3x=0相交于A、B两点,若圆心M到直线AB的距离为 ,求圆M的方程. 作业:
P132习题4.2A组:4,6,9,10.4.2.3 直线与圆的方程的应用问题提出 通过直线与圆的方程,可以确定直线与圆、圆和圆的位置关系,对于生产、生活实践以及平面几何中与直线和圆有关的问题,我们可以建立直角坐标系,通过直线与圆的方程,将其转化为代数问题来解决.对此,我们必须掌握解决问题的基本思想和方法.直线与圆
的方程的应用知识探究:直线与圆的方程在实际生活中的应用 问题Ⅰ:一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70 km处, 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?思考1:解决这个问题的本质是什么?思考2:你有什么办法判断轮船航线是否经过台风圆域?思考3:如图所示建立直角坐标系,取10km为长度单位,那么轮船航线所在直线和台风圆域边界所在圆的方程分别是什么?思考4:直线4x+7y-28=0与圆x2+y2=9的位置关系如何?对问题Ⅰ应作怎样的回答?问题Ⅱ:如图是某圆拱形桥一孔圆拱的示意图. 这个圆的圆拱跨度AB=20m,拱高OP=4m,建造时每间隔4m需要用一根支柱支撑,求支柱A2P2的高度(精确到0.01m)思考1:你能用几何法求支柱A2P2的高度吗?思考2:如图所示建立直角坐标系,那么求支柱A2P2的高度,化归为求一个什么问题?思考4:利用这个圆的方程可求得点P2的纵坐标是多少?问题Ⅱ的答案如何?思考3:取1m为长度单位,如何求圆拱所在圆的方程?x2+(y+10.5)2=14.52 知识探究:直线与圆的方程在平面几何中的应用 问题Ⅱ:已知内接于圆的四边形的对角线互相垂直,求证:圆心到一边的距离等于这条边所对边长的一半.思考1:许多平面几何问题常利用“坐标法”来解决,首先要做的工作是建立适当的直角坐标系,在本题中应如何选取坐标系?思考2:如图所示建立直角坐标系,设四边形的四个顶点分别为点 A(a,0),B(0,b),C(c,0), D(0,d),那么BC边的长为多少?思考3:四边形ABCD的外接圆圆心M的坐标如何?思考4:如何计算圆心M到直线AD的距离|MN|?思考5:由上述计算可得|BC|=2|MN|,从而命题成立.你能用平面几何知识证明这个命题吗?理论迁移 例1 如图,在Rt△AOB中,|OA|=4,|OB|=3,∠AOB=90°,点P是△AOB内切圆上任意一点,求点P到顶点A、O、B的距离的平方和的最大值和最小值. 例2 如图,圆O1和圆O2的半径都等于1,圆心距为4,过动点P分别作圆O1和圆O2的切线,切点为M、N,且使得|PM|= |PN|,试求点P的运动轨迹是什么曲线?
作业:
P132练习:1,2,3,4.
P133习题4.2B组:1,2,3. 4.3 空间直角坐标系 4.3.1 空间直角坐标系 问题提出 对于直线上的点,我们可以通过数轴来确定点的位置;对于平面上的点,我们可以通过平面直角坐标系来确定点的位置;对于空间中的点,我们也希望建立适当的坐标系来确定点的位置. 因此,如何在空间中建立坐标系,就成为我们需要研究的课题.空间直角坐标系知识探究(一):空间直角坐标系 思考1:数轴上的点M的坐标用一个实数x表示,它是一维坐标;平面上的点M的坐标用一对有序实数(x,y)表示,它是二维坐标.设想:对于空间中的点的坐标,需要几个实数表示?思考2:平面直角坐标系由两条互相垂直的数轴组成,设想:空间直角坐标系由几条数轴组成?其相对位置关系如何? 三条交于一点且两两互相垂直的数轴 思考3:在空间中,取三条交于一点且两两互相垂直的数轴:x轴、y轴、z轴,组成空间直角坐标系Oxyz,在平面上如何画空间直角坐标系? ∠xOy=135°∠yOz=90° 思考4:在空间直角坐标系中,对三条数轴的方向作如下约定:伸出右手,拇指指向为x轴正方向,食指指向为y轴正方向,中指指向为z轴正方向,并称这样的坐标系为右手直角坐标系.那么下列空间直角坐标系中哪些是右手直角坐标系?思考5:在空间直角坐标系Oxyz中,其中点O叫做坐标原点,x轴、y轴、z轴叫做坐标轴,通过每两个坐标轴的平面叫做坐标平面,并分别称为xOy平面、yOz平面、xOz平面.这三个坐标平面的位置关系如何?思考6:如图,在长方体ABCD-A1B1C1D1中,以点D为坐标原点建立空间右手直角坐标系,那么x轴、y轴、z轴
应如何选取?思考7:在空间直角坐标系Oxyz中,三个坐标平面将空间分成几个部分?知识探究(二)空间直角坐标系中点的坐标 思考1:在平面直角坐标系中,点M的横坐标、纵坐标的含义如何? 思考2:在空间直角坐标系中,设点M为空间的一个定点,过点M分别作垂直于x轴、y轴、z轴的平面,垂足为A、B、C. 设点A、B、C在x轴、y轴、z轴上的坐标分别为x、y、z,那么点M的位置与有序实数组(x,y,z)是一个什么对应关系? 思考3:上述有序实数组(x,y,z)称为点M的空间坐标,其中x、y、z分别叫做点M的横坐标、纵坐标、
竖坐标,这三个坐标的值一定是正数吗?xyz思考4:x轴、y轴、z轴上的点的坐标有何特点?xOy平面、yOz平面、xOz平面上的点的坐标有何特点?x轴上的点:(x,0,0)xOy平面上的点:(x,y,0)思考5:设点M的坐标为(a,b,c)过点M分别作xOy平面、yOz平面、xOz平面的垂线,那么三个垂足的坐标分别如何?A(a,b,0)B(0,b,c)C(a,0,c)思考6:设点M的坐标为(x,y,z)那么点M关于x轴、y轴、z轴及原点对称的点的坐标分别是什么?M(x,y,z)N(x,-y,-z)思考7:设点A(x1,y1,z1),点 B(x2,y2,z2),则线段AB的中点M的坐标如何?理论迁移 例1 如图,在长方体OABC-D′A′B′C′中,|OA|=3,|OC|=4,
|OD′|=2,写出长方体各顶点的坐标. 例2 结晶体的基本单位称为晶胞,下图是食盐晶胞的示意图(可看成是八个棱长为0.5的小正方体堆积成的正方体),其中色点代表钠原子,白点代表氯原子.如图建立直角坐标系Oxyz,试写出全部钠原子所在位置的坐标.作业:
P136练习:1,2,3.
P138习题4.3A组:2. 4.3.2 空间两点间的距离公式 问题提出 1. 在平面直角坐标系中两点间的距离公式是什么? 2. 在空间直角坐标系中,若已知两个点的坐标,则这两点之间的距离是惟一确定的,我们希望有一个求两点间距离的计算公式,对此,我们从理论上进行探究.空间两点间的距离公式知识探究(一):与坐标原点的距离公式 思考1:在空间直角坐标系中,坐标轴上的点A(x,0,0),B(0,y,0),C(0,0,z),与坐标原点O的距离分别是什么?|OA|=|x||OB|=|y||OC|=|z|思考2:在空间直角坐标系中,坐标平面上的点A(x,y,0),B(0,y,z),C(x,0,z),与坐标原点O的距离分别是什么?思考3:在空间直角坐标系中,设点 P(x,y,z)在xOy平面上的射影为M,则点M的坐标是什么?|PM|,|OM|的值分别是什么?M(x,y,0)|PM|=|z|思考4:基于上述分析,你能得到点 P(x,y,z)与坐标原点O的距离公式吗?思考5:在空间直角坐标系中,方程 x2+y2+z2=r2(r>0为常数)表示什么图形是什么? 知识探究(二):空间两点间的距离公式 在空间中,设点P1(x1,y1,z1),P2(x2,y2,z2)在xOy平面上的射影分别为M、N.思考1:点M、N之间的距离如何?思考2:若直线P1P2垂直于xOy平面,则点P1、P2之间的距离如何?|P1P2|=|z1-z2|思考3:若直线P1P2平行于xOy平面,则点P1、P2之间的距离如何?思考4:若直线P1P2 是xOy平面的一条斜线,则点P1、P2的距离如何计算?思考5:在上述图形背景下,点P1(x1,y1,z1)与P2(x2,y2,z2)之间的距离是
它对任意两点P1、P2都成立吗? 例1 在空间中,已知点A(1, 0, -1),B (4, 3, -1),求A、B两点之间的距离.理论迁移 例2 已知两点 A(-4, 1, 7)和B(3, 5, -2),点P在z轴上,若|PA|=|PB|,求点P的坐标. 例3 如图,点P、Q分别在棱长为1的正方体的对角线AB和棱CD上运动,求P、Q两点间的距离的最小值,并指出此时P、Q两点的位置. 作业:
P138练习:1,2,3,4.
