数学四年级下人教版1.2 乘、除法的意义和各部分间的关系 课件(16张)
文档属性
| 名称 | 数学四年级下人教版1.2 乘、除法的意义和各部分间的关系 课件(16张) |  | |
| 格式 | zip | ||
| 文件大小 | 848.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-01 17:43:36 | ||
图片预览






文档简介
(共16张PPT)
第一单元
(四则运算)
(一)乘法的意义
4+4+4+4 + 4=( )×( ) =( )
问题:什么是乘法?
求几个相同加数的和的简便运算,叫做乘法。
相乘的两个数叫做因数。
因数×因数
乘得的数叫做积。
=积
16+16+16+=( )×( ) =( )
48
3
5
4
16
20
一、复习旧知
问题:什么是除法?
已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
(二)除法的意义
在除法中,已知的积叫做被除数,已知的因数叫做除数,所求的因数叫做商。
根据24 × 15=360写出两个除法算式是:
( )、
( )。
360÷24=15
360÷15=24
商=被除数÷除数
一、复习旧知
1. 乘法各部分间的关系
积=因数×因数
问题:如果知道积与一个因数,能求出另一个因数吗?
因数=积÷另一个因数
(三)乘、除法各部分间的关系
2. 除法各部分间的关系
商=被除数÷除数
除数=被除数÷商
被除数=商×除数
问题:如果知道被除数和商,能求出除数吗?
问题:如果知道除数和商,能求出被除数吗?
一、复习旧知
问题:乘法与除法间有什么关系?
除法是乘法的逆运算。
3. 乘法与除法间的关系
(三)乘、除法各部分间的关系
(或乘法是除法的逆运算)
一、复习旧知
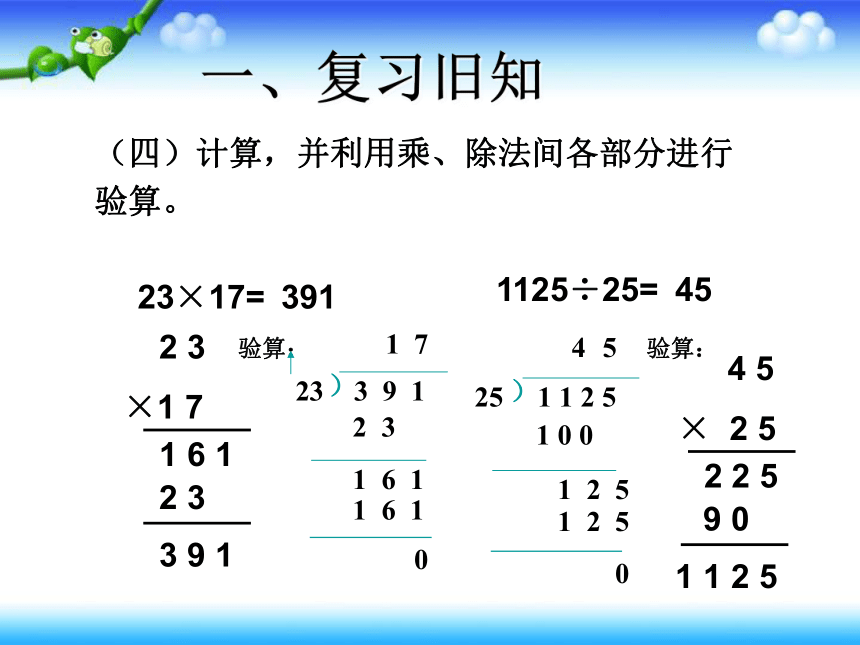
(四)计算,并利用乘、除法间各部分进行验算。
23×17=
1125÷25=
2 3
×1 7
1 6 1
2 3
3 9 1
验算:
)
3 9 1
23
1
2 3
1 6 1
7
1 6 1
0
1 2 5
)
1 1 2 5
25
4
1 0 0
1 2 5
5
0
4 5
× 2 5
2 2 5
9 0
1 1 2 5
391
45
验算:
一、复习旧知
想一想:在有余数的除法里,被除数与商、除数和余数之间有什么关系?
19÷6=( )……( )
被除数=商×除数+余数
1. 有余数的除法各部分间的关系
(一)乘、除法各部分间的关系
二、探究规律,明确意义
190÷60=( )……( )
3
1
3
10
(除数不能是0,余数总比除数小。)
除数=(被除数-余数)÷商
三、巩固新知
被除数 除数 商 余数
225 21
18 23 6
478 13 10
1、填表
10
15
420
36
被除数=商×除数+余数
除数=(被除数-余数)÷商
问题:说一说你是根据什么得出结果的?
217÷70 = 785÷24=
)
2 1 7
70
3
2 1 0
7
3……7
)
7 8 5
24
3
20
7 2
6 5
2
4 8
1 7
32……17
2、计算,并利用乘、除法间各部分进行验算。
三、巩固新知
验算:
7 0
× 3
2 1 0
+ 7
2 1 7
验算:
3 2
× 2 4
1 2 8
6 4
7 6 8
+ 1 7
7 8 5
3. 对号入座。
三、巩固新知
(1)如果○÷△=□,那么下面各式中( )是正确的。
A. ○=△×□
B. ○=□ ÷ △
C. △= ○ ×□
(2)如果☆÷△=□……3,那么下面各式中( )是正确的。
A. △= ☆ ÷ □+3
B. ☆ = □ × △ +3
C. ☆ = □ × △
(3)如果 ○ ÷△=12……9,当除数最小时,被除数是( )。
A. 120
B. 129
C. 111
A
B
B
这节课,你有什么收获?
课堂总结
有余数除法各部分之间的关系:
被除数=商×除数+余数
(除数不能是0,余数总比除数小。)
除数=(被除数-余数)÷商
课堂作业
1、填空:
(1)在有余数的除法中,被除数=( ) ×除数+( )
(2)一个数除以25,商是12,余数10,这个数是( )。
(3)被除数是460,商和余数都是20,除数是( )
(4)已知( ) ÷ 15=24……( ),当余数最大时,
被除数是( )。
2、计算并验算:
(1)964÷27=
(2)1000÷45=
四、布置课外作业
1:第7页练习二,第5、6题。
2:《同步导学与优化训练》
第3页内容
第一单元
(四则运算)
(一)乘法的意义
4+4+4+4 + 4=( )×( ) =( )
问题:什么是乘法?
求几个相同加数的和的简便运算,叫做乘法。
相乘的两个数叫做因数。
因数×因数
乘得的数叫做积。
=积
16+16+16+=( )×( ) =( )
48
3
5
4
16
20
一、复习旧知
问题:什么是除法?
已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
(二)除法的意义
在除法中,已知的积叫做被除数,已知的因数叫做除数,所求的因数叫做商。
根据24 × 15=360写出两个除法算式是:
( )、
( )。
360÷24=15
360÷15=24
商=被除数÷除数
一、复习旧知
1. 乘法各部分间的关系
积=因数×因数
问题:如果知道积与一个因数,能求出另一个因数吗?
因数=积÷另一个因数
(三)乘、除法各部分间的关系
2. 除法各部分间的关系
商=被除数÷除数
除数=被除数÷商
被除数=商×除数
问题:如果知道被除数和商,能求出除数吗?
问题:如果知道除数和商,能求出被除数吗?
一、复习旧知
问题:乘法与除法间有什么关系?
除法是乘法的逆运算。
3. 乘法与除法间的关系
(三)乘、除法各部分间的关系
(或乘法是除法的逆运算)
一、复习旧知
(四)计算,并利用乘、除法间各部分进行验算。
23×17=
1125÷25=
2 3
×1 7
1 6 1
2 3
3 9 1
验算:
)
3 9 1
23
1
2 3
1 6 1
7
1 6 1
0
1 2 5
)
1 1 2 5
25
4
1 0 0
1 2 5
5
0
4 5
× 2 5
2 2 5
9 0
1 1 2 5
391
45
验算:
一、复习旧知
想一想:在有余数的除法里,被除数与商、除数和余数之间有什么关系?
19÷6=( )……( )
被除数=商×除数+余数
1. 有余数的除法各部分间的关系
(一)乘、除法各部分间的关系
二、探究规律,明确意义
190÷60=( )……( )
3
1
3
10
(除数不能是0,余数总比除数小。)
除数=(被除数-余数)÷商
三、巩固新知
被除数 除数 商 余数
225 21
18 23 6
478 13 10
1、填表
10
15
420
36
被除数=商×除数+余数
除数=(被除数-余数)÷商
问题:说一说你是根据什么得出结果的?
217÷70 = 785÷24=
)
2 1 7
70
3
2 1 0
7
3……7
)
7 8 5
24
3
20
7 2
6 5
2
4 8
1 7
32……17
2、计算,并利用乘、除法间各部分进行验算。
三、巩固新知
验算:
7 0
× 3
2 1 0
+ 7
2 1 7
验算:
3 2
× 2 4
1 2 8
6 4
7 6 8
+ 1 7
7 8 5
3. 对号入座。
三、巩固新知
(1)如果○÷△=□,那么下面各式中( )是正确的。
A. ○=△×□
B. ○=□ ÷ △
C. △= ○ ×□
(2)如果☆÷△=□……3,那么下面各式中( )是正确的。
A. △= ☆ ÷ □+3
B. ☆ = □ × △ +3
C. ☆ = □ × △
(3)如果 ○ ÷△=12……9,当除数最小时,被除数是( )。
A. 120
B. 129
C. 111
A
B
B
这节课,你有什么收获?
课堂总结
有余数除法各部分之间的关系:
被除数=商×除数+余数
(除数不能是0,余数总比除数小。)
除数=(被除数-余数)÷商
课堂作业
1、填空:
(1)在有余数的除法中,被除数=( ) ×除数+( )
(2)一个数除以25,商是12,余数10,这个数是( )。
(3)被除数是460,商和余数都是20,除数是( )
(4)已知( ) ÷ 15=24……( ),当余数最大时,
被除数是( )。
2、计算并验算:
(1)964÷27=
(2)1000÷45=
四、布置课外作业
1:第7页练习二,第5、6题。
2:《同步导学与优化训练》
第3页内容
