17.2.1 平面直角坐标系同步练习
文档属性
| 名称 | 17.2.1 平面直角坐标系同步练习 |

|
|
| 格式 | docx | ||
| 文件大小 | 663.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-01 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
17.2.1 平面直角坐标系同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.平面直角坐标系是由两条原点重合、互相垂直具有相同单位长度的数轴组成的;两条坐标轴把平面分成四个区域,分别称为第 一二、三、四象限.
2.平面内点的坐标:点的坐标的表示方法横在前在后,中间用逗号隔开,用括号括起来,3.平面直角坐标系中的点和有序实数对是一一对应的.
4.各象限内点的坐标的特征,
【设点P(a,b)】:
①各象限点的特征:
第一象限(+,+) ; 第二象限(—,+) ;
第三象限(一,一);第四象限(+,一).
②特殊位置点的特征:
若点P在x轴上,则b=0 ;
若点P在y轴上,则a=0 ;
若点P在一、三象限角平分线上,则a=b ;
若点P在二、四象限角平分线上,则a+b=0.
5.关于x 轴、y 轴、原点对称的点的坐标的特点.关于x轴对称的点“x”不变,“y”互为相反数;而关于y 轴对称的点“x”互为相反数,“y”不变.
基础知识和能力拓展精练
一、选择题
1.根据下列表述,能确定具体位置的是( )
A. 某电影院2排 B. 大桥南路 C. 北偏东30° D. 东经108°,北纬43°
2.一个有序数对可以( )
A. 确定一个点的位置 B. 确定两个点的位置
C. 确定一个或两个点的位置 D. 不能确定点的位置
3.如果电影票上的“5排2号”记作(5,2),那么(4,3)表示( )
A. 3排5号 B. 5排3号 C. 4排3号 D. 3排4号
4.已知点不在第一象限,则点在( )
A. x轴正半轴上 B. x轴负半轴上 C. y轴正半轴上 D. y轴负半轴上
5.如图,笑脸盖住的点的坐标可能为( )
A. (-2,3) B. (3,-4) C. (-4,-6) D. (5,2)
6.甲、乙两名同学下棋,甲执圆子,乙执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示,甲将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,甲放的位置是( )
A. (-2,1) B. (-1,1) C. (-1,0) D. (-1,2)
7.已知点P(a+5,9+a)位于二象限的角平分线上,则a的值为( )
A. 3 B. -3 C. -7 D. -1
8.已知点A(4,2),B(-2,2),则直线AB ( )
A. 平行于x轴 B. 平行于y轴 C. 经过原点 D. 以上都有可能
9.点A(a + 1,a)关于x轴对称的点在第一象限,则a的取值范围是( )
A. -1< a < 0 B. C. D.
10.如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为( )
A. (2017,1) B. (2017,0) C. (2017,2) D. (2016,0)
二、填空题
11.在我们生活中通常用两种方法来确定物体的位置.如小岛A在码头O的南偏东60°方向的14千米处,若以码头O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1千米为单位长度建立平面直角坐标系,则小岛A也可表示成____________
12.点P(1,-2)关于x轴对称的点的坐标是_____.
13.点P在第二象限,到x轴距离为3,到y轴距离为2,点P 坐标______ 。
14.已知点A(-2,0),B(3,0),点C在y轴上,且S三角形ABC=10,则点C的坐标为____________.
15.某人从A点出发,向北偏东60°方向走了10米到达B点,再从B点向南偏西15°方向走了10米到达c点,则∠ABC等于 ____________ 。
16.如图所示,线段, , 的长度分别为, , ,且平分.若将点表示为,点表示为,则点可表示为__________.
17.已知点A(2,4)与点B(b-1,2a)关于原点对称,则ab=____________.
三、解答题
18.已知A(a-3,a2-4),求a的值及点A的坐标.
(1)当点A在x轴上;
(2)当点A在y轴上.
19.已知点在第三象限.
()化简.
()点到轴的距离是到轴的倍,请求出点坐标.
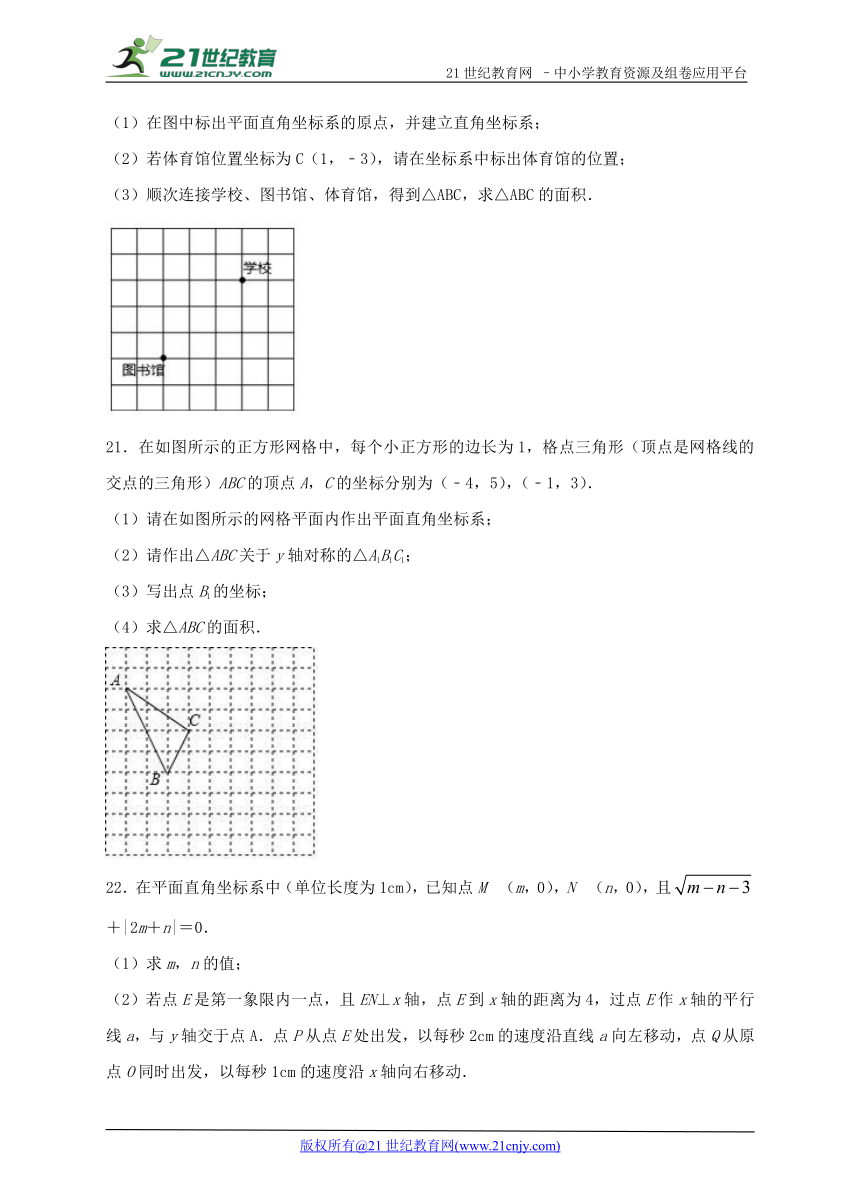
20.如图,方格纸中每个小方格都是边长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:
(1)在图中标出平面直角坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
21.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标;
(4)求△ABC的面积.
22.在平面直角坐标系中(单位长度为1cm),已知点M (m,0),N (n,0),且+|2m+n|=0.
(1)求m,n的值;
(2)若点E是第一象限内一点,且EN⊥x轴,点E到x轴的距离为4,过点E作x轴的平行线a,与y轴交于点A.点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.
①经过几秒PQ平行于y轴?
②若某一时刻以A,O,Q,P为顶点的四边形的面积是10cm2,求此时点P的坐标.
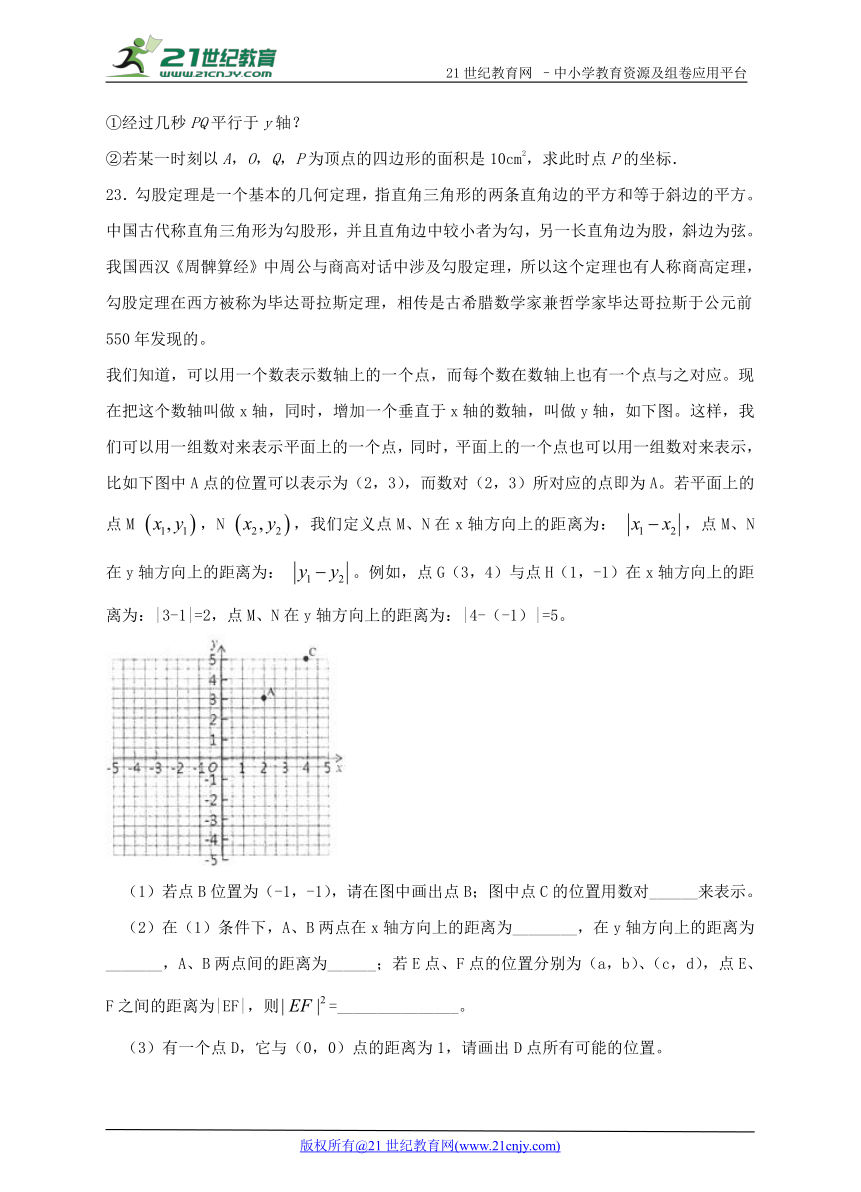
23.勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦。我国西汉《周髀算经》中周公与商高对话中涉及勾股定理,所以这个定理也有人称商高定理,勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年发现的。
我们知道,可以用一个数表示数轴上的一个点,而每个数在数轴上也有一个点与之对应。现在把这个数轴叫做x轴,同时,增加一个垂直于x轴的数轴,叫做y轴,如下图。这样,我们可以用一组数对来表示平面上的一个点,同时,平面上的一个点也可以用一组数对来表示,比如下图中A点的位置可以表示为(2,3),而数对(2,3)所对应的点即为A。若平面上的点M ,N ,我们定义点M、N在x轴方向上的距离为: ,点M、N在y轴方向上的距离为: 。例如,点G(3,4)与点H(1,-1)在x轴方向上的距离为:|3-1|=2,点M、N在y轴方向上的距离为:|4-(-1)|=5。
(1)若点B位置为(-1,-1),请在图中画出点B;图中点C的位置用数对______来表示。
(2)在(1)条件下,A、B两点在x轴方向上的距离为________,在y轴方向上的距离为_______,A、B两点间的距离为______;若E点、F点的位置分别为(a,b)、(c,d),点E、F之间的距离为|EF|,则=_______________。
(3)有一个点D,它与(0,0)点的距离为1,请画出D点所有可能的位置。
参考答案
1.D
【解析】A. 某电影院2排,不能确定具体位置,故本选项错误;
B. 大桥南路,不能确定具体位置,故本选项错误;
C. 北偏东东30°,不能确定具体位置,故本选项错误;
D. 东经108°,北纬43°,能确定具体位置,故本选项正确。
故选D.
2.A
【解析】一对有序数对可以确定一个点的位置,故选A.
3.C
【解析】试题分析:由“5排2号”记作(5,2)可知横坐标表示排,纵坐标表示号,
所以(4,3)表示4排3号,
故选C.
4.C
【解析】试题解析:点不在第一象限,则在第二象限,
点在y轴正半轴上,
故选C.
5.A
【解析】解:由图形可得:笑脸盖住的点的坐标可能为(﹣2,3).故选A.
点睛:此题主要考查了点的坐标,得出笑脸的横纵坐标符号是解题关键.
6.B
【解析】根据题目中给出的两个棋子的坐标可知,原图中最右侧的圆子位于坐标原点O,并且可以确定如图①所示的平面直角坐标系.
在画出上述平面直角坐标系的棋盘上依次标注各选项所描述的第4枚圆子的位置(如图②至图⑤;该圆子所在位置用相应的选项名称在图中标注).
观察图②至图⑤可以看出,在四个选项中,只有按照B选项给出的坐标放置第4枚圆子才能使整个图形成为轴对称图形(图③中的虚线表示该图形的对称轴).
故本题应选B.
点睛:
本题综合考查了图形对称性和平面直角坐标系的相关知识. 根据题目中给出的两个棋子的坐标确定符合题意的平面直角坐标系是本题的一个关键点. 识别所构成的图形是否是轴对称图形是本题的另一个关键点.
7.C
【解析】根据题意得a+5+9+a=0,解得a= 7.
故选:C.
8.A
【解析】A(4,2),B(-2,2)
∴点A到x轴的距离为2,点B到x轴的距离为2
且A、B都在x轴上方
∴AB平行于x轴,故选A.
点睛:此题是研究平面直角坐标系中,两个点所连线段与坐标轴的位置关系,需要对点到直线的距离有着明确地理解,而且此题属于较简单的判断线与坐标轴位置关系的一类问题。
9.A
【解析】∵点A(a+1,a)关于x轴的对称点在第一象限,
∴点A(a+1,a)在第四象限,
∴,
解得:-1点睛:本题考查了关于x轴、y轴对称的点的坐标,解一元一次不等式组的知识点,首先根据题意可得P(a+1,a)在第四象限,再根据第四象限内点的坐标符号可得点P的横坐标为正,纵坐标为负,再列出不等式组,求解集即可.
10.A
【解析】根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),∴第4次运动到点(4,0),第5次接着运动到点(5,1),…,∴横坐标为运动次数,经过第2017次运动后,动点P的横坐标为2017,纵坐标为1,0,2,0,每4次一轮,∴经过第2017次运动后,动点P的纵坐标为:2017÷4=504余1,故纵坐标为四个数中第三个,即为1,∴经过第2017次运动后,动点P的坐标是(2017,1).
故选:A.
11.(7,-7)
【解析】试题分析:过点A作AC⊥x轴于C,
在Rt△OAC中,∠AOC=90°-60°=30°,OA=14千米, 则AC=7千米,OC=7千米,
因而小岛A所在位置的坐标是(7,-7).
12.(1,2)
【解析】点P(1,-2)关于x轴对称的点的坐标是(1,2).
故答案为(1,2).
13.( -2,3)
【解析】因为点P到x轴距离为3,到y轴距离为2,
所以x=2或-2,y=3或-3,
又因为点P在第二象限,
所以P(-2,3).
故答案是:(-2,3).
14.(0,4)或(0,-4)
【解析】设C(0,y),
BC=10,
5|y|=10,
y. C(0,4)或(0,-4).
故答案为(0,4)或(0,-4).
15.45°
【解析】
如图所示:∵∠EAB=∠ABD=60°,∠DBC=15°,
∴∠ABC=∠ABD ∠DBC=45°.
故答案为:45°.
16.(2,75°)
【解析】由线段OB、OC、OA的长度分别是1、2、3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),
∴∠AOB=90°,∠AOC=45°,
则C点可表示为(2, 75°).
故答案为:(2 , 75°).
17.2.
【解析】由题意,得
b 1= 2,2a= 4,
解得b= 1,a= 2,
∴ab=( 2) ×( 1)=2,
故答案为:2.
18.(1) a=±2,点A的坐标为(-1,0)或(-5,0);(2) a=3,点A的坐标为(0,5).
【解析】试题分析:(1)根据点在x轴上时,纵坐标为0,求出a的值,进而求出点A的坐标;
(2)根据点在y轴上时,横坐标为0,求出a的值,进而求出点A的坐标.
试题解析:(1)∵A在x轴上,
∴a2-4=0,即a=±2,
∴a-3=-1或-5,
∴点A的坐标为(-1,0)或(-5,0).
(2)∵A在y轴上,
∴a-3=0,即a=3,
∴a2-4=5,
∴点A的坐标为(0,5).
19.(1)6;(2)(-4,-2)
【解析】【试题分析】
(1)点在第三象限.得, ,解得: ,则原式= ;
(2)到轴的距离为横坐标的绝对值,即, 到轴的距离为纵坐标的绝对值,即,由题意得: ,解得,则点的坐标为.
【试题解析】
()∵在第三象限,
∴即,
即,
综上, ,
∴.
()∵到轴的距离为, 到轴的距离为,
∴,
∴,
∴点的坐标为.
【方法点睛】本题目是平面直角坐标系的背景下的一道不等式组的运用问题,根据象限的坐标特征,列出不等式组,求出参数x的取值范围,从而化简关于x的代数式;理解点到坐标轴的距离,到横轴的距离是纵坐标的绝对值,到纵轴的而距离是横坐标的绝对值.
20.(1)答案见解析;(2)答案见解析;(3)4.5.
【解析】试题分析:
(1)根据点B的坐标,确定原点的位置,再建立直角坐标系;
(2)根据点C的坐标,确定C点的位置;
(3)△ABC的过三个顶点的长方形的面积减去三个三角形的面积.
试题解析:
(1)如图, (2)如图,
(3)S△ABC=3×4﹣×2×1﹣×1×4﹣×3×3=4.5
21.(1)作图见解析;(2)作图见解析;(3)(2,1);(4)4.
【解析】试题分析:(1)根据A点坐标建立平面直角坐标系即可;
(2)作出各点关于y轴的对称点,再顺次连接即可;
(3)根据点B1在坐标系中的位置写出其坐标即可;
(4)利用矩形的面积减去三个顶点上三角形的面积即可.
解:(1)根据题意可作出如图所示的坐标系;
(2)如图,△A1B1C1即为所求;
(3)由图可知,B1(2,1);
(4)S△ABC=3×4﹣×2×4﹣×2×1﹣×2×3=12﹣4﹣1﹣3=4.
22.(1)m=-3,n=6;(2)①2秒;②(4,4)或(-,4).
【解析】试题分析:(1)根据平方根和绝对值的性质得出
解方程组即可;
(2)①设秒后平行于轴,由于,所以当时,四边形是平行四边形,那么平行于轴,根据列出关于的方程,解方程即可;
②设秒后四边形的面积为,根据四边形的面积= 列出关于的方程,进而求出点的坐标.
试题解析:(1)依题意,得解得
(2)①设经过x秒PQ平行于y轴,
依题意,得6 2x=x解得x=2,
②当点P在y轴右侧时,
依题意,得
解得x=1,
此时点P的坐标为(4,4),
当点P在y轴左侧时,
依题意,得
解得
此时点P的坐标为
23.(1)点C(4,5);(2)3,4,5;(a-c)+(b-d)(3)见图中:圆.
【解析】试题分析:(1)根据有序数对的含义解答,明确有序数对前后两个数表示的含义;
(2)根据两点在坐标轴方向的距离含义或解答;两点间的距离则根据勾股定理解答.
(3)与(0,0)点的距离为1的点在以(0,0)为圆心,以1为半径的圆上.
解:(1)点B的位置如图,点C的位置用数对(4,5)来表示;
(2)A、B两点在x轴方向上的距离为: ;
A、B两点在y轴方向上的距离为: ;
A、B两点间的距离为: ;
∵E、F两点在x轴方向上的距离为: ,
E、F两点在y轴方向上的距离为: ,
.
(3)如图,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
17.2.1 平面直角坐标系同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.平面直角坐标系是由两条原点重合、互相垂直具有相同单位长度的数轴组成的;两条坐标轴把平面分成四个区域,分别称为第 一二、三、四象限.
2.平面内点的坐标:点的坐标的表示方法横在前在后,中间用逗号隔开,用括号括起来,3.平面直角坐标系中的点和有序实数对是一一对应的.
4.各象限内点的坐标的特征,
【设点P(a,b)】:
①各象限点的特征:
第一象限(+,+) ; 第二象限(—,+) ;
第三象限(一,一);第四象限(+,一).
②特殊位置点的特征:
若点P在x轴上,则b=0 ;
若点P在y轴上,则a=0 ;
若点P在一、三象限角平分线上,则a=b ;
若点P在二、四象限角平分线上,则a+b=0.
5.关于x 轴、y 轴、原点对称的点的坐标的特点.关于x轴对称的点“x”不变,“y”互为相反数;而关于y 轴对称的点“x”互为相反数,“y”不变.
基础知识和能力拓展精练
一、选择题
1.根据下列表述,能确定具体位置的是( )
A. 某电影院2排 B. 大桥南路 C. 北偏东30° D. 东经108°,北纬43°
2.一个有序数对可以( )
A. 确定一个点的位置 B. 确定两个点的位置
C. 确定一个或两个点的位置 D. 不能确定点的位置
3.如果电影票上的“5排2号”记作(5,2),那么(4,3)表示( )
A. 3排5号 B. 5排3号 C. 4排3号 D. 3排4号
4.已知点不在第一象限,则点在( )
A. x轴正半轴上 B. x轴负半轴上 C. y轴正半轴上 D. y轴负半轴上
5.如图,笑脸盖住的点的坐标可能为( )
A. (-2,3) B. (3,-4) C. (-4,-6) D. (5,2)
6.甲、乙两名同学下棋,甲执圆子,乙执方子.如图,棋盘中心方子的位置用(-1,0)表示,右下角方子的位置用(0,-1)表示,甲将第4枚圆子放入棋盘后,所有棋子构成一个轴对称图形,甲放的位置是( )
A. (-2,1) B. (-1,1) C. (-1,0) D. (-1,2)
7.已知点P(a+5,9+a)位于二象限的角平分线上,则a的值为( )
A. 3 B. -3 C. -7 D. -1
8.已知点A(4,2),B(-2,2),则直线AB ( )
A. 平行于x轴 B. 平行于y轴 C. 经过原点 D. 以上都有可能
9.点A(a + 1,a)关于x轴对称的点在第一象限,则a的取值范围是( )
A. -1< a < 0 B. C. D.
10.如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为( )
A. (2017,1) B. (2017,0) C. (2017,2) D. (2016,0)
二、填空题
11.在我们生活中通常用两种方法来确定物体的位置.如小岛A在码头O的南偏东60°方向的14千米处,若以码头O为坐标原点,正东方向为x轴的正方向,正北方向为y轴的正方向,1千米为单位长度建立平面直角坐标系,则小岛A也可表示成____________
12.点P(1,-2)关于x轴对称的点的坐标是_____.
13.点P在第二象限,到x轴距离为3,到y轴距离为2,点P 坐标______ 。
14.已知点A(-2,0),B(3,0),点C在y轴上,且S三角形ABC=10,则点C的坐标为____________.
15.某人从A点出发,向北偏东60°方向走了10米到达B点,再从B点向南偏西15°方向走了10米到达c点,则∠ABC等于 ____________ 。
16.如图所示,线段, , 的长度分别为, , ,且平分.若将点表示为,点表示为,则点可表示为__________.
17.已知点A(2,4)与点B(b-1,2a)关于原点对称,则ab=____________.
三、解答题
18.已知A(a-3,a2-4),求a的值及点A的坐标.
(1)当点A在x轴上;
(2)当点A在y轴上.
19.已知点在第三象限.
()化简.
()点到轴的距离是到轴的倍,请求出点坐标.
20.如图,方格纸中每个小方格都是边长为1个单位的正方形,若学校位置坐标为A(2,1),图书馆位置坐标为B(﹣1,﹣2),解答以下问题:
(1)在图中标出平面直角坐标系的原点,并建立直角坐标系;
(2)若体育馆位置坐标为C(1,﹣3),请在坐标系中标出体育馆的位置;
(3)顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.
21.在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标;
(4)求△ABC的面积.
22.在平面直角坐标系中(单位长度为1cm),已知点M (m,0),N (n,0),且+|2m+n|=0.
(1)求m,n的值;
(2)若点E是第一象限内一点,且EN⊥x轴,点E到x轴的距离为4,过点E作x轴的平行线a,与y轴交于点A.点P从点E处出发,以每秒2cm的速度沿直线a向左移动,点Q从原点O同时出发,以每秒1cm的速度沿x轴向右移动.
①经过几秒PQ平行于y轴?
②若某一时刻以A,O,Q,P为顶点的四边形的面积是10cm2,求此时点P的坐标.
23.勾股定理是一个基本的几何定理,指直角三角形的两条直角边的平方和等于斜边的平方。中国古代称直角三角形为勾股形,并且直角边中较小者为勾,另一长直角边为股,斜边为弦。我国西汉《周髀算经》中周公与商高对话中涉及勾股定理,所以这个定理也有人称商高定理,勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年发现的。
我们知道,可以用一个数表示数轴上的一个点,而每个数在数轴上也有一个点与之对应。现在把这个数轴叫做x轴,同时,增加一个垂直于x轴的数轴,叫做y轴,如下图。这样,我们可以用一组数对来表示平面上的一个点,同时,平面上的一个点也可以用一组数对来表示,比如下图中A点的位置可以表示为(2,3),而数对(2,3)所对应的点即为A。若平面上的点M ,N ,我们定义点M、N在x轴方向上的距离为: ,点M、N在y轴方向上的距离为: 。例如,点G(3,4)与点H(1,-1)在x轴方向上的距离为:|3-1|=2,点M、N在y轴方向上的距离为:|4-(-1)|=5。
(1)若点B位置为(-1,-1),请在图中画出点B;图中点C的位置用数对______来表示。
(2)在(1)条件下,A、B两点在x轴方向上的距离为________,在y轴方向上的距离为_______,A、B两点间的距离为______;若E点、F点的位置分别为(a,b)、(c,d),点E、F之间的距离为|EF|,则=_______________。
(3)有一个点D,它与(0,0)点的距离为1,请画出D点所有可能的位置。
参考答案
1.D
【解析】A. 某电影院2排,不能确定具体位置,故本选项错误;
B. 大桥南路,不能确定具体位置,故本选项错误;
C. 北偏东东30°,不能确定具体位置,故本选项错误;
D. 东经108°,北纬43°,能确定具体位置,故本选项正确。
故选D.
2.A
【解析】一对有序数对可以确定一个点的位置,故选A.
3.C
【解析】试题分析:由“5排2号”记作(5,2)可知横坐标表示排,纵坐标表示号,
所以(4,3)表示4排3号,
故选C.
4.C
【解析】试题解析:点不在第一象限,则在第二象限,
点在y轴正半轴上,
故选C.
5.A
【解析】解:由图形可得:笑脸盖住的点的坐标可能为(﹣2,3).故选A.
点睛:此题主要考查了点的坐标,得出笑脸的横纵坐标符号是解题关键.
6.B
【解析】根据题目中给出的两个棋子的坐标可知,原图中最右侧的圆子位于坐标原点O,并且可以确定如图①所示的平面直角坐标系.
在画出上述平面直角坐标系的棋盘上依次标注各选项所描述的第4枚圆子的位置(如图②至图⑤;该圆子所在位置用相应的选项名称在图中标注).
观察图②至图⑤可以看出,在四个选项中,只有按照B选项给出的坐标放置第4枚圆子才能使整个图形成为轴对称图形(图③中的虚线表示该图形的对称轴).
故本题应选B.
点睛:
本题综合考查了图形对称性和平面直角坐标系的相关知识. 根据题目中给出的两个棋子的坐标确定符合题意的平面直角坐标系是本题的一个关键点. 识别所构成的图形是否是轴对称图形是本题的另一个关键点.
7.C
【解析】根据题意得a+5+9+a=0,解得a= 7.
故选:C.
8.A
【解析】A(4,2),B(-2,2)
∴点A到x轴的距离为2,点B到x轴的距离为2
且A、B都在x轴上方
∴AB平行于x轴,故选A.
点睛:此题是研究平面直角坐标系中,两个点所连线段与坐标轴的位置关系,需要对点到直线的距离有着明确地理解,而且此题属于较简单的判断线与坐标轴位置关系的一类问题。
9.A
【解析】∵点A(a+1,a)关于x轴的对称点在第一象限,
∴点A(a+1,a)在第四象限,
∴,
解得:-1
10.A
【解析】根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),∴第4次运动到点(4,0),第5次接着运动到点(5,1),…,∴横坐标为运动次数,经过第2017次运动后,动点P的横坐标为2017,纵坐标为1,0,2,0,每4次一轮,∴经过第2017次运动后,动点P的纵坐标为:2017÷4=504余1,故纵坐标为四个数中第三个,即为1,∴经过第2017次运动后,动点P的坐标是(2017,1).
故选:A.
11.(7,-7)
【解析】试题分析:过点A作AC⊥x轴于C,
在Rt△OAC中,∠AOC=90°-60°=30°,OA=14千米, 则AC=7千米,OC=7千米,
因而小岛A所在位置的坐标是(7,-7).
12.(1,2)
【解析】点P(1,-2)关于x轴对称的点的坐标是(1,2).
故答案为(1,2).
13.( -2,3)
【解析】因为点P到x轴距离为3,到y轴距离为2,
所以x=2或-2,y=3或-3,
又因为点P在第二象限,
所以P(-2,3).
故答案是:(-2,3).
14.(0,4)或(0,-4)
【解析】设C(0,y),
BC=10,
5|y|=10,
y. C(0,4)或(0,-4).
故答案为(0,4)或(0,-4).
15.45°
【解析】
如图所示:∵∠EAB=∠ABD=60°,∠DBC=15°,
∴∠ABC=∠ABD ∠DBC=45°.
故答案为:45°.
16.(2,75°)
【解析】由线段OB、OC、OA的长度分别是1、2、3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),
∴∠AOB=90°,∠AOC=45°,
则C点可表示为(2, 75°).
故答案为:(2 , 75°).
17.2.
【解析】由题意,得
b 1= 2,2a= 4,
解得b= 1,a= 2,
∴ab=( 2) ×( 1)=2,
故答案为:2.
18.(1) a=±2,点A的坐标为(-1,0)或(-5,0);(2) a=3,点A的坐标为(0,5).
【解析】试题分析:(1)根据点在x轴上时,纵坐标为0,求出a的值,进而求出点A的坐标;
(2)根据点在y轴上时,横坐标为0,求出a的值,进而求出点A的坐标.
试题解析:(1)∵A在x轴上,
∴a2-4=0,即a=±2,
∴a-3=-1或-5,
∴点A的坐标为(-1,0)或(-5,0).
(2)∵A在y轴上,
∴a-3=0,即a=3,
∴a2-4=5,
∴点A的坐标为(0,5).
19.(1)6;(2)(-4,-2)
【解析】【试题分析】
(1)点在第三象限.得, ,解得: ,则原式= ;
(2)到轴的距离为横坐标的绝对值,即, 到轴的距离为纵坐标的绝对值,即,由题意得: ,解得,则点的坐标为.
【试题解析】
()∵在第三象限,
∴即,
即,
综上, ,
∴.
()∵到轴的距离为, 到轴的距离为,
∴,
∴,
∴点的坐标为.
【方法点睛】本题目是平面直角坐标系的背景下的一道不等式组的运用问题,根据象限的坐标特征,列出不等式组,求出参数x的取值范围,从而化简关于x的代数式;理解点到坐标轴的距离,到横轴的距离是纵坐标的绝对值,到纵轴的而距离是横坐标的绝对值.
20.(1)答案见解析;(2)答案见解析;(3)4.5.
【解析】试题分析:
(1)根据点B的坐标,确定原点的位置,再建立直角坐标系;
(2)根据点C的坐标,确定C点的位置;
(3)△ABC的过三个顶点的长方形的面积减去三个三角形的面积.
试题解析:
(1)如图, (2)如图,
(3)S△ABC=3×4﹣×2×1﹣×1×4﹣×3×3=4.5
21.(1)作图见解析;(2)作图见解析;(3)(2,1);(4)4.
【解析】试题分析:(1)根据A点坐标建立平面直角坐标系即可;
(2)作出各点关于y轴的对称点,再顺次连接即可;
(3)根据点B1在坐标系中的位置写出其坐标即可;
(4)利用矩形的面积减去三个顶点上三角形的面积即可.
解:(1)根据题意可作出如图所示的坐标系;
(2)如图,△A1B1C1即为所求;
(3)由图可知,B1(2,1);
(4)S△ABC=3×4﹣×2×4﹣×2×1﹣×2×3=12﹣4﹣1﹣3=4.
22.(1)m=-3,n=6;(2)①2秒;②(4,4)或(-,4).
【解析】试题分析:(1)根据平方根和绝对值的性质得出
解方程组即可;
(2)①设秒后平行于轴,由于,所以当时,四边形是平行四边形,那么平行于轴,根据列出关于的方程,解方程即可;
②设秒后四边形的面积为,根据四边形的面积= 列出关于的方程,进而求出点的坐标.
试题解析:(1)依题意,得解得
(2)①设经过x秒PQ平行于y轴,
依题意,得6 2x=x解得x=2,
②当点P在y轴右侧时,
依题意,得
解得x=1,
此时点P的坐标为(4,4),
当点P在y轴左侧时,
依题意,得
解得
此时点P的坐标为
23.(1)点C(4,5);(2)3,4,5;(a-c)+(b-d)(3)见图中:圆.
【解析】试题分析:(1)根据有序数对的含义解答,明确有序数对前后两个数表示的含义;
(2)根据两点在坐标轴方向的距离含义或解答;两点间的距离则根据勾股定理解答.
(3)与(0,0)点的距离为1的点在以(0,0)为圆心,以1为半径的圆上.
解:(1)点B的位置如图,点C的位置用数对(4,5)来表示;
(2)A、B两点在x轴方向上的距离为: ;
A、B两点在y轴方向上的距离为: ;
A、B两点间的距离为: ;
∵E、F两点在x轴方向上的距离为: ,
E、F两点在y轴方向上的距离为: ,
.
(3)如图,
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
