17.2.2 函数的图象同步练习
文档属性
| 名称 | 17.2.2 函数的图象同步练习 |

|
|
| 格式 | docx | ||
| 文件大小 | 570.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-01 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
17.2.2 函数的图象同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.函数图象上每一点的坐标(x、y)代表了函数的一对对应值 ,它的横坐标x表示自变量的某一个值,纵坐标y表示与该自变量对应的函数值.
2.用描点法画函数图象的一般步骤为列表、描点、连线.
3.函数图象是将某种代数规律“转化”为几何图形,使其规律更加直观.首先要明确函数图象中横轴、纵轴所表示的实际意义,其次理解图象中每段图象所代表的实际意义.
基础知识和能力拓展精练
一、选择题
1.甲、乙两人沿相同的路线从A到B匀速行驶,A,B两地间的路程为20 km,他们行进的路程s(km)与甲、乙出发的时间t(h)之间关系的图象如图所示,根据图象信息,下列说法正确的是( )
甲的速度是4 km/h B. 乙的速度是10 km/h
C. 乙比甲晚出发1 h D. 甲比乙晚到B地3 h
2.在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊.如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s).根据相关信息判断,下列说法中错误的是( )
A. 喜羊羊与灰太狼最初的距离是30m B. 灰太狼用15s追上了喜羊羊
C. 灰太狼跑了60m追上了喜羊羊 D. 灰太狼追上喜羊羊时,喜羊羊跑了60m
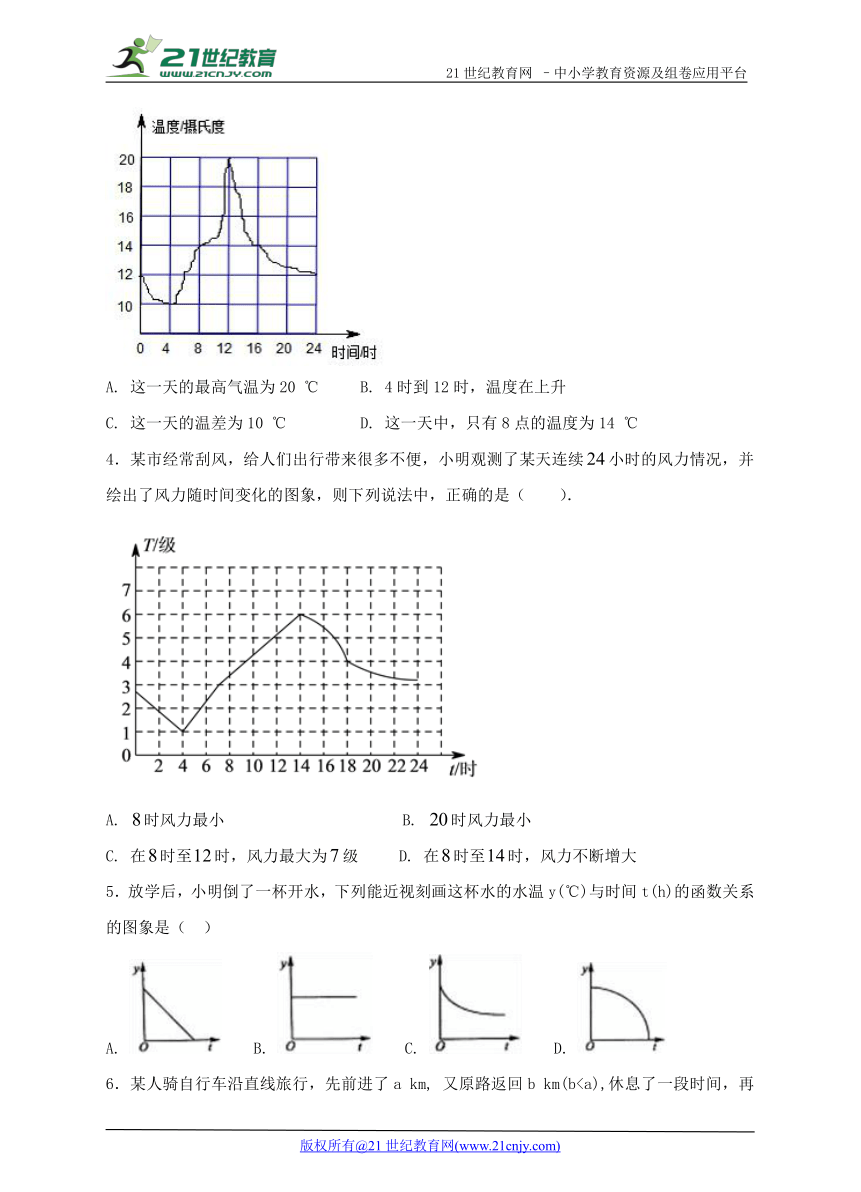
3.如图为某一天气温随时间的变化图,则下列说法不正确的是( )
A. 这一天的最高气温为20 ℃ B. 4时到12时,温度在上升
C. 这一天的温差为10 ℃ D. 这一天中,只有8点的温度为14 ℃
4.某市经常刮风,给人们出行带来很多不便,小明观测了某天连续小时的风力情况,并绘出了风力随时间变化的图象,则下列说法中,正确的是( ).
A. 时风力最小 B. 时风力最小
C. 在时至时,风力最大为级 D. 在时至时,风力不断增大
5.放学后,小明倒了一杯开水,下列能近视刻画这杯水的水温y(℃)与时间t(h)的函数关系的图象是( )
A. B. C. D.
6.某人骑自行车沿直线旅行,先前进了a km, 又原路返回b km(bA. B. C. D.
7.某地出租车计费方式如下:3 km以内只收起步价8元,超过3 km的除收起步价外,每超出1 km另加收2元;不足1 km的按1 km计费.则能反映该地出租车行驶路程x(km)与所收费用y(元)之间的函数关系的图象是( )
8.爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )
A. B. C. D.
9.一天,小芳去学校,她离开家不久,想起课本忘在家里,于是立即返回家里找到课本再去学校.下列四个图象中,能近似地刻画小芳这天上学过程的是( )
A. B. C. D.
10.(2016青海省)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B. C. D.
二、填空题
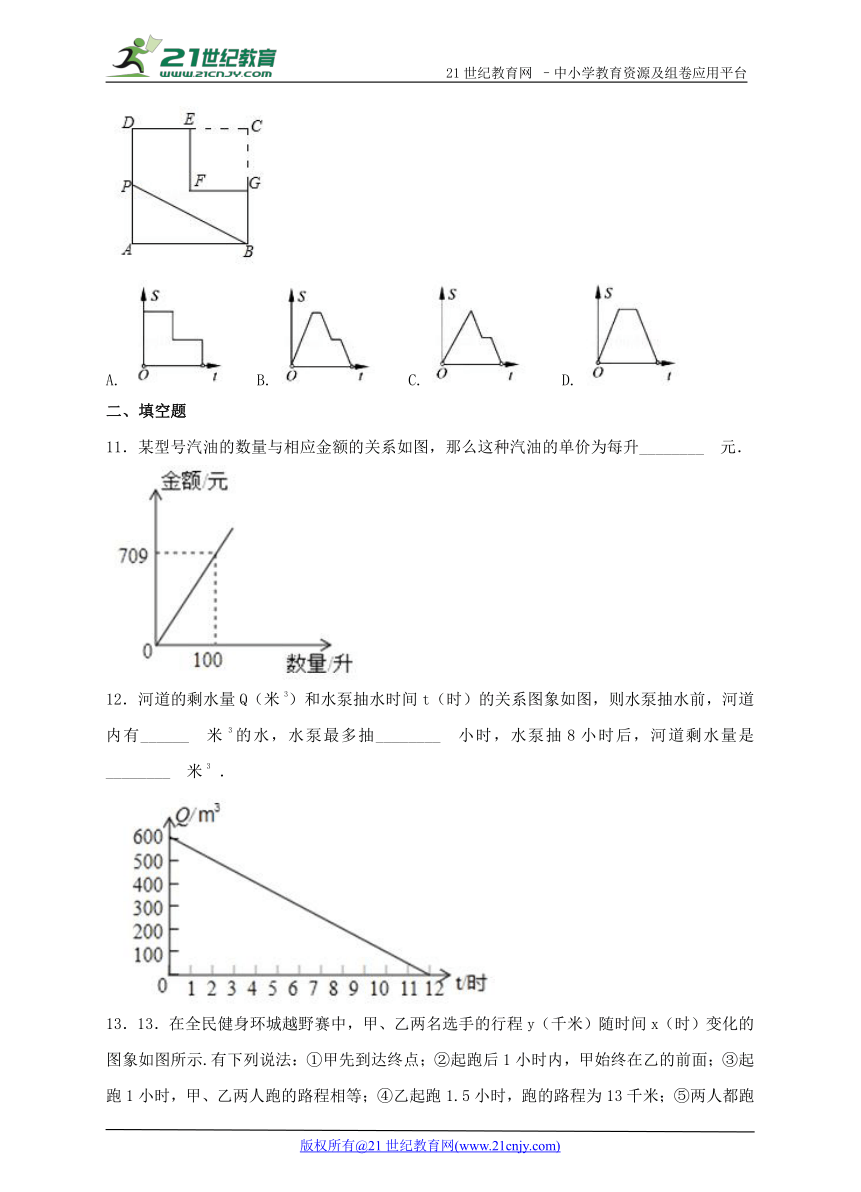
11.某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升________ 元.
12.河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有______ 米3的水,水泵最多抽________ 小时,水泵抽8小时后,河道剩水量是________ 米3 .
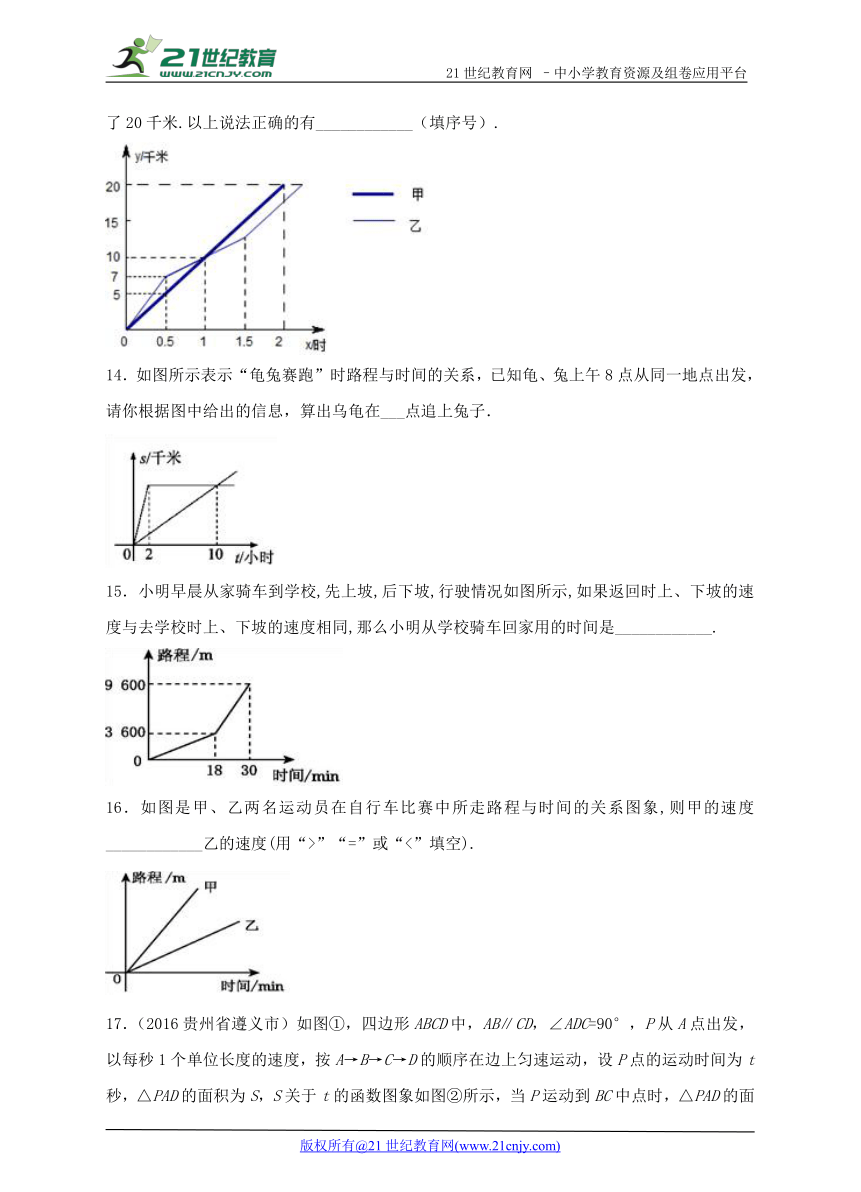
13.13.在全民健身环城越野赛中,甲、乙两名选手的行程y(千米)随时间x(时)变化的图象如图所示.有下列说法:①甲先到达终点;②起跑后1小时内,甲始终在乙的前面;③起跑1小时,甲、乙两人跑的路程相等;④乙起跑1.5小时,跑的路程为13千米;⑤两人都跑了20千米.以上说法正确的有____________(填序号).
14.如图所示表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8点从同一地点出发,请你根据图中给出的信息,算出乌龟在___点追上兔子.
15.小明早晨从家骑车到学校,先上坡,后下坡,行驶情况如图所示,如果返回时上、下坡的速度与去学校时上、下坡的速度相同,那么小明从学校骑车回家用的时间是____________.
16.如图是甲、乙两名运动员在自行车比赛中所走路程与时间的关系图象,则甲的速度____________乙的速度(用“>”“=”或“<”填空).
17.(2016贵州省遵义市)如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为______.
三、解答题
18.温度的变化是人们经常谈论的话题,请根据图象与同伴讨论某天温度变化的情况.
(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
19.小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)图象表示了哪两个变量的关系 哪个是自变量 哪个是因变量
(2)10时和13时,他分别离家多远
(3)他到达离家最远的地方是什么时间 离家多远
(4)11时到12时他行驶了多少千米
(5)他可能在哪段时间内休息,并吃午餐
(6)他由离家最远的地方返回时的平均速度是多少
20.某机动车出发前油箱内有油42L.行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答问题.
(1)机动车行驶几小时后加油?
(2)中途加油________L;
(3)如果加油站距目的地还有240km,车速为40km/h,要到达目的地,油箱中的油是否够用?并说明原因.
21.已知y与x的关系的图象如图所示,根据图象回答下列问题:
(1)确定自变量x的取值范围.
(2)当x=-4,-2,4时,y的值分别是多少
(3)当y=0,4时,x的值分别是多少
(4)当x取何值时,y的值最大 当x取何值时,y的值最小
(5)当x的值在什么范围内时,y随x的增大而增大 当x的值在什么范围内时,y随x的增大而减小
22.下面是一位病人的体温记录图,看图回答下列问题:
(1)护士每隔几小时给病人量一次体温?
(2)这位病人的最高体温是多少摄氏度?最低体温是多少摄氏度?
(3)他在4月8日12时的体温是多少摄氏度?
(4)图中的横线表示什么?
(5)从图中看,这位病人的病情是恶化还是好转?
23.甲、乙两人共同加工一批零件,从工作开始到加工完这批零件,两人恰好同时工作6小时,两人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图像如图所示,根据信息回答下列问题:
()请解释图中点C的实际意义;
()求出甲、乙在整个过程中的函数表达式(并注明自变量的范围);
()如果甲、乙两人完成同样数量的零件时,甲比乙少用1小时,那么此时甲、乙两人各自完成多少个零件?
参考答案
1.B
【解析】A. 甲的速度是20÷4=5 km/h,故不正确;
B. 乙的速度是20÷2=10 km/h,故正确;
C. 由图像知,乙和甲同时出发,故不正确;
D. 由图像知,甲比乙晚到B地2 h,故不正确;
故选B.
点睛:本题主要考查学生的读图获取信息的能力,要注意分析其中的“关键点”,还要善于分析各图象的变化趋势.
2.D
【解析】观察图象可得,喜羊羊与灰太狼最初的距离是100-70=30m,选项A正确;由横坐标看出,15秒灰太狼追上了喜羊羊,选项B正确;由纵坐标看出,灰太狼跑了100-40=60米追上喜羊羊,选项C正确;由纵坐标看出,灰太狼追上喜羊羊时喜羊羊跑了70-40=30米,选项D错误;故选D.
3.D
【解析】观察可知这一天的最高气温为20 ℃,故A选项正确; 4时到12时,温度在上升,故B选项正确;这一天的温差为20-10=10 ℃ ,故C选项正确;这一天中, 8点、16点的温度为14 ℃,故D选项错误,
故选D.
4.D
【解析】观察图象可知,4时风力最小,故A、B选项错误;在8时至14时,风力最大为7级,故C选项错误;D. 在8时至14时,风力不断增大,正确,
故选D.
5.C
【解析】根据题意可知,这杯水的水温与时间的关系是:水温随着时间的增大而逐渐减小,最后达到一个固定的温度.故选C.
6.C
【解析】∵先前进了a km, 又原路返回b km(b∵先前进了a km, 又原路返回b km(b∵开始时骑着自行车走的快,图像比较陡;后来推着自行车走的慢,图像比较缓,∴C正确.
故选C.
7.D
【解析】由题意知:当x≤3时,y=8,图象是一段与x轴平行的线段;故A、C错误;
当x>3时,y=8+2(x-3),(x为整数),故图象是分段函数.
故选:D.
点睛:本题考查了分段函数的问题,分段函数是在不同区间有不同对应分式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.
8.C
【解析】图象应分三个阶段,第一阶段:慢步到离家较远的中山公园,在这个阶段,离家的距离随时间的增大而增大;第二阶段:打了一会儿太极拳,这一阶段离家的距离不随时间的变化而改变.第三阶段:坐公交车回家,在这个阶段,离家的距离随时间的增大而减小,因公交车的速度大于跑步的速度,第三阶段的图象要比第一阶段的图象陡.故选C.
点睛:本题主要考查了函数的图象问题,在解题时要根据实际情况确定出函数的图象是解题的关键.
9.D
【解析】试题解析:小芳离开家不久,即离家一段路程,此时A、B、C、D都符合,发现把课本忘在家里,于是返回了家里找到了课本,即又返回家,离家的距离是0,此时C、D都符合,又去学校,即离家越来越远,此时只有D返回,只有D符合情境;
故选D.
点睛:本题主要考查学生的观察图象的能力,同时也考查了学生的叙述能力,用了数形结合思想,题型比较好,但是一道比较容易出错的题目.
10.B
【解析】解:当点P在AD上时,△ABP的底AB不变,高增大,所以△ABP的面积S随着时间t的增大而增大;
当点P在DE上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在EF上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小而减小;
当点P在FG上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在GB上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小而减小;
故选B.
11.7.09
【解析】由图像可得,100升汽油共用709元,所以这种汽油的单价为每升7.09元.
12. 600 12 200
【解析】观察图象可知, 水泵抽水前,河道内有600米3的水,水泵最多抽12 小时,水泵抽8小时后,河道剩水量是600-600÷12×8=200米3.
13.①③④⑤
【解析】从图象上来看,甲先到达终点,所以①正确;
甲乙的起跑点是一样的,在起跑后到1小时之间,乙的图形都比甲的图形高,说明起跑后1小时内,乙在甲的前面,所以②错误;
通过图象观察,一小时时该点的纵坐标是10,所以第1小时两人都跑了10千米,所以③正确;
观察图形,当时间为2小时时候,乙已经到达终点,而此时甲还没到达,所以甲比乙先到达终点是错误的,所以③错误;观察图形,从0.5到时1.5这段时间内的乙的速度是一样的,0.5到1时,乙跑了10-7=3千米,所以1.5小时时,乙跑的路为10+3=13千米,所以④正确;观察图象可知,两人都跑了20千米,所以⑤正确,
综上所述,正确的有①③④⑤,
故答案为:①③④⑤.
【点睛】本题考查了函数图象,解答本题的关键是会观察函数图象,得出有用的信息,从而来判断正确还是错误.
14.18
【解析】两个函数图形的交点的横坐标是10,说明10小时后,乌龟追上兔子,此时的时间为:8+10=18时.
故答案为:18.
15.37.2 min
【解析】由图中可以看出:上坡速度为: =200/ min,下坡速度为: =500/ min,
返回途中,上下坡的路程正好相反,所用时间为: =7.2+30=37.2 min。
故答案为:37.2 min.
16.>
【解析】根据题意:甲的位移增加得快,故甲的速度大于乙的速度.
故答案为>.
点睛:此题主要考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小,通过图象得到函数是随自变量的增大或减小的快慢.
17.5
【解析】解:由图象可知,AB+BC=6,AB+BC+CD=10,∴CD=4,根据题意可知,当P点运动到C点时,△PAD的面积最大,S△PAD=×AD×DC=8,∴AD=4,又∵S△ABD=×AB×AD=2,∴AB=1,∴当P点运动到BC中点时,△PAD的面积=×(AB+CD)×AD=5,故答案为:5.
18.答案见解析
【解析】试题分析:(1)观察图象,可知最高温度为37℃,时间为15时,最低温度是23℃,时间为3时;
(2)由(1)中得出的最高温度-最低温度即可求出温差,也可求得经过的时间;
(3)观察图象可求解.
试题解析:(1)根据图象可以看出:这一天的最高温度是37℃,是在15时到达的,最低温度是23℃,是在3时达到的;
(2)温差为:37 23=14(℃),经过的时间为:15 3=12(时);
(3)从3时到15时温度在上升,在0时到3时、15时到24时温度在下降.
19.(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看出12:00时他到达离家最远的地方,离家30千米. (4)由图象看出11时距家19千米,12时距家30千米,11时到12时他行驶了30- 19=11(千米). (5)由图象看出12:00~13:00时距离没变且时间较长,得12:00~13:00休息并吃午餐. (6)由图象看出回家时用了2小时,路程是30千米,所以回家的平均速度是30÷2=15(千米/时).
20.(1)5小时(2)24(3)油箱中的油刚好够用.
【解析】试题分析:(1)根据图象可得,5小时时,机动车内的油从12升变为了36升,故5小时后加油;
(2)用36-12即可;
(3)首先计算出耗油量,再根据路程和速度计算出行驶240km的时间,然后用时间乘以耗油量可得所消耗的油,和油箱里的油量进行比较即可.
试题解析:(1)根据图象可直接得到:机动车行驶5小时后加油;
(2)36 12=24(L);
(3)够用,
耗油量:(42 12)÷5=6(km/L),240÷40=6(小时), 6×6=36(L),
故够用.
21.答案见解析
【解析】试题分析:(1)根据函数图象的横坐标,可得答案;
(2)根据自变量的值与函数值的对应关系,可得相应的函数值;
(3)根据函数值,可得相应自变量的值;
(4)根据函数图象的最高点、最低点,可得相应自变量的值;
(5)根据函数图象的横坐标,可得函数的增区间.
试题解析:(1)-4≤x≤4.
(2)y的值分别是2,-2,0.
(3)当y=0时,x的值是-3,-1或4;
当y=4时,x的值是1.5.
(4)当x=1.5时,y的值最大;
当x=-2时,y的值最小.
(5)当-2≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2和1.5≤x≤4时,y随x的增大而减小.
22.见解析
【解析】试题分析:
(1)(3)观察、分析图象中的数据信息,结合题意即可得到相应答案;
(4)图中的横线表示人的正常体温:37℃;
(5)由图象可知,这位病人的体温逐渐趋近于正常体温,由此可知病人的病情在好转.
试题解析:
(1)观察图象可得:护士每隔6小时给病人测量一次体温;
(2)观察图象可得:这位病人的最高体温是39.5℃,最低体温是36.8℃;
(3)这位病人4月8日12时的体温是37.5℃;
(4)图中的横线表示人的正常体温是37℃;
(5)从图象的变化趋势看可以看出,这位病人的体温逐渐趋近于正常体温,
∴这位病人的病情在好转.
23.()甲、乙两人工作了小时,完成的零件数相同,为个;()甲: 时, , 时, .乙: 时, , 时, ;()当甲、乙两人各自完成40个和95个零件的时候,甲比乙少用.
【解析】试题分析:(1)观察可知点C的实际意义是甲、乙都工件了5小时,完成的零件数相同;
(2)利用待定系数法分别分段进行求解即可;
(3)分时间段进行讨论即可得.
试题解析:()甲、乙两人工作了小时,完成的零件数相同,为个;
()甲: 时, ,
时, .
乙: 时, ,
时, ,
()①当,则, .
②当,则, .
③当时,甲比乙完成慢,不会出现甲比乙少用这种情况,
综上所述,当甲、乙两人各自完成40个和95个零件的时候,甲比乙少用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
17.2.2 函数的图象同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.函数图象上每一点的坐标(x、y)代表了函数的一对对应值 ,它的横坐标x表示自变量的某一个值,纵坐标y表示与该自变量对应的函数值.
2.用描点法画函数图象的一般步骤为列表、描点、连线.
3.函数图象是将某种代数规律“转化”为几何图形,使其规律更加直观.首先要明确函数图象中横轴、纵轴所表示的实际意义,其次理解图象中每段图象所代表的实际意义.
基础知识和能力拓展精练
一、选择题
1.甲、乙两人沿相同的路线从A到B匀速行驶,A,B两地间的路程为20 km,他们行进的路程s(km)与甲、乙出发的时间t(h)之间关系的图象如图所示,根据图象信息,下列说法正确的是( )
甲的速度是4 km/h B. 乙的速度是10 km/h
C. 乙比甲晚出发1 h D. 甲比乙晚到B地3 h
2.在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊.如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s).根据相关信息判断,下列说法中错误的是( )
A. 喜羊羊与灰太狼最初的距离是30m B. 灰太狼用15s追上了喜羊羊
C. 灰太狼跑了60m追上了喜羊羊 D. 灰太狼追上喜羊羊时,喜羊羊跑了60m
3.如图为某一天气温随时间的变化图,则下列说法不正确的是( )
A. 这一天的最高气温为20 ℃ B. 4时到12时,温度在上升
C. 这一天的温差为10 ℃ D. 这一天中,只有8点的温度为14 ℃
4.某市经常刮风,给人们出行带来很多不便,小明观测了某天连续小时的风力情况,并绘出了风力随时间变化的图象,则下列说法中,正确的是( ).
A. 时风力最小 B. 时风力最小
C. 在时至时,风力最大为级 D. 在时至时,风力不断增大
5.放学后,小明倒了一杯开水,下列能近视刻画这杯水的水温y(℃)与时间t(h)的函数关系的图象是( )
A. B. C. D.
6.某人骑自行车沿直线旅行,先前进了a km, 又原路返回b km(b
7.某地出租车计费方式如下:3 km以内只收起步价8元,超过3 km的除收起步价外,每超出1 km另加收2元;不足1 km的按1 km计费.则能反映该地出租车行驶路程x(km)与所收费用y(元)之间的函数关系的图象是( )
8.爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家.下面能反映当天小华的爷爷离家的距离y与时间x的函数关系的大致图象是( )
A. B. C. D.
9.一天,小芳去学校,她离开家不久,想起课本忘在家里,于是立即返回家里找到课本再去学校.下列四个图象中,能近似地刻画小芳这天上学过程的是( )
A. B. C. D.
10.(2016青海省)如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
A. B. C. D.
二、填空题
11.某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升________ 元.
12.河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有______ 米3的水,水泵最多抽________ 小时,水泵抽8小时后,河道剩水量是________ 米3 .
13.13.在全民健身环城越野赛中,甲、乙两名选手的行程y(千米)随时间x(时)变化的图象如图所示.有下列说法:①甲先到达终点;②起跑后1小时内,甲始终在乙的前面;③起跑1小时,甲、乙两人跑的路程相等;④乙起跑1.5小时,跑的路程为13千米;⑤两人都跑了20千米.以上说法正确的有____________(填序号).
14.如图所示表示“龟兔赛跑”时路程与时间的关系,已知龟、兔上午8点从同一地点出发,请你根据图中给出的信息,算出乌龟在___点追上兔子.
15.小明早晨从家骑车到学校,先上坡,后下坡,行驶情况如图所示,如果返回时上、下坡的速度与去学校时上、下坡的速度相同,那么小明从学校骑车回家用的时间是____________.
16.如图是甲、乙两名运动员在自行车比赛中所走路程与时间的关系图象,则甲的速度____________乙的速度(用“>”“=”或“<”填空).
17.(2016贵州省遵义市)如图①,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图②所示,当P运动到BC中点时,△PAD的面积为______.
三、解答题
18.温度的变化是人们经常谈论的话题,请根据图象与同伴讨论某天温度变化的情况.
(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
19.小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)图象表示了哪两个变量的关系 哪个是自变量 哪个是因变量
(2)10时和13时,他分别离家多远
(3)他到达离家最远的地方是什么时间 离家多远
(4)11时到12时他行驶了多少千米
(5)他可能在哪段时间内休息,并吃午餐
(6)他由离家最远的地方返回时的平均速度是多少
20.某机动车出发前油箱内有油42L.行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答问题.
(1)机动车行驶几小时后加油?
(2)中途加油________L;
(3)如果加油站距目的地还有240km,车速为40km/h,要到达目的地,油箱中的油是否够用?并说明原因.
21.已知y与x的关系的图象如图所示,根据图象回答下列问题:
(1)确定自变量x的取值范围.
(2)当x=-4,-2,4时,y的值分别是多少
(3)当y=0,4时,x的值分别是多少
(4)当x取何值时,y的值最大 当x取何值时,y的值最小
(5)当x的值在什么范围内时,y随x的增大而增大 当x的值在什么范围内时,y随x的增大而减小
22.下面是一位病人的体温记录图,看图回答下列问题:
(1)护士每隔几小时给病人量一次体温?
(2)这位病人的最高体温是多少摄氏度?最低体温是多少摄氏度?
(3)他在4月8日12时的体温是多少摄氏度?
(4)图中的横线表示什么?
(5)从图中看,这位病人的病情是恶化还是好转?
23.甲、乙两人共同加工一批零件,从工作开始到加工完这批零件,两人恰好同时工作6小时,两人各自加工零件的个数y(个)与加工时间x(小时)之间的函数图像如图所示,根据信息回答下列问题:
()请解释图中点C的实际意义;
()求出甲、乙在整个过程中的函数表达式(并注明自变量的范围);
()如果甲、乙两人完成同样数量的零件时,甲比乙少用1小时,那么此时甲、乙两人各自完成多少个零件?
参考答案
1.B
【解析】A. 甲的速度是20÷4=5 km/h,故不正确;
B. 乙的速度是20÷2=10 km/h,故正确;
C. 由图像知,乙和甲同时出发,故不正确;
D. 由图像知,甲比乙晚到B地2 h,故不正确;
故选B.
点睛:本题主要考查学生的读图获取信息的能力,要注意分析其中的“关键点”,还要善于分析各图象的变化趋势.
2.D
【解析】观察图象可得,喜羊羊与灰太狼最初的距离是100-70=30m,选项A正确;由横坐标看出,15秒灰太狼追上了喜羊羊,选项B正确;由纵坐标看出,灰太狼跑了100-40=60米追上喜羊羊,选项C正确;由纵坐标看出,灰太狼追上喜羊羊时喜羊羊跑了70-40=30米,选项D错误;故选D.
3.D
【解析】观察可知这一天的最高气温为20 ℃,故A选项正确; 4时到12时,温度在上升,故B选项正确;这一天的温差为20-10=10 ℃ ,故C选项正确;这一天中, 8点、16点的温度为14 ℃,故D选项错误,
故选D.
4.D
【解析】观察图象可知,4时风力最小,故A、B选项错误;在8时至14时,风力最大为7级,故C选项错误;D. 在8时至14时,风力不断增大,正确,
故选D.
5.C
【解析】根据题意可知,这杯水的水温与时间的关系是:水温随着时间的增大而逐渐减小,最后达到一个固定的温度.故选C.
6.C
【解析】∵先前进了a km, 又原路返回b km(b
故选C.
7.D
【解析】由题意知:当x≤3时,y=8,图象是一段与x轴平行的线段;故A、C错误;
当x>3时,y=8+2(x-3),(x为整数),故图象是分段函数.
故选:D.
点睛:本题考查了分段函数的问题,分段函数是在不同区间有不同对应分式的函数,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.
8.C
【解析】图象应分三个阶段,第一阶段:慢步到离家较远的中山公园,在这个阶段,离家的距离随时间的增大而增大;第二阶段:打了一会儿太极拳,这一阶段离家的距离不随时间的变化而改变.第三阶段:坐公交车回家,在这个阶段,离家的距离随时间的增大而减小,因公交车的速度大于跑步的速度,第三阶段的图象要比第一阶段的图象陡.故选C.
点睛:本题主要考查了函数的图象问题,在解题时要根据实际情况确定出函数的图象是解题的关键.
9.D
【解析】试题解析:小芳离开家不久,即离家一段路程,此时A、B、C、D都符合,发现把课本忘在家里,于是返回了家里找到了课本,即又返回家,离家的距离是0,此时C、D都符合,又去学校,即离家越来越远,此时只有D返回,只有D符合情境;
故选D.
点睛:本题主要考查学生的观察图象的能力,同时也考查了学生的叙述能力,用了数形结合思想,题型比较好,但是一道比较容易出错的题目.
10.B
【解析】解:当点P在AD上时,△ABP的底AB不变,高增大,所以△ABP的面积S随着时间t的增大而增大;
当点P在DE上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在EF上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小而减小;
当点P在FG上时,△ABP的底AB不变,高不变,所以△ABP的面积S不变;
当点P在GB上时,△ABP的底AB不变,高减小,所以△ABP的面积S随着时间t的减小而减小;
故选B.
11.7.09
【解析】由图像可得,100升汽油共用709元,所以这种汽油的单价为每升7.09元.
12. 600 12 200
【解析】观察图象可知, 水泵抽水前,河道内有600米3的水,水泵最多抽12 小时,水泵抽8小时后,河道剩水量是600-600÷12×8=200米3.
13.①③④⑤
【解析】从图象上来看,甲先到达终点,所以①正确;
甲乙的起跑点是一样的,在起跑后到1小时之间,乙的图形都比甲的图形高,说明起跑后1小时内,乙在甲的前面,所以②错误;
通过图象观察,一小时时该点的纵坐标是10,所以第1小时两人都跑了10千米,所以③正确;
观察图形,当时间为2小时时候,乙已经到达终点,而此时甲还没到达,所以甲比乙先到达终点是错误的,所以③错误;观察图形,从0.5到时1.5这段时间内的乙的速度是一样的,0.5到1时,乙跑了10-7=3千米,所以1.5小时时,乙跑的路为10+3=13千米,所以④正确;观察图象可知,两人都跑了20千米,所以⑤正确,
综上所述,正确的有①③④⑤,
故答案为:①③④⑤.
【点睛】本题考查了函数图象,解答本题的关键是会观察函数图象,得出有用的信息,从而来判断正确还是错误.
14.18
【解析】两个函数图形的交点的横坐标是10,说明10小时后,乌龟追上兔子,此时的时间为:8+10=18时.
故答案为:18.
15.37.2 min
【解析】由图中可以看出:上坡速度为: =200/ min,下坡速度为: =500/ min,
返回途中,上下坡的路程正好相反,所用时间为: =7.2+30=37.2 min。
故答案为:37.2 min.
16.>
【解析】根据题意:甲的位移增加得快,故甲的速度大于乙的速度.
故答案为>.
点睛:此题主要考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,能够通过图象得到函数是随自变量的增大,知道函数值是增大还是减小,通过图象得到函数是随自变量的增大或减小的快慢.
17.5
【解析】解:由图象可知,AB+BC=6,AB+BC+CD=10,∴CD=4,根据题意可知,当P点运动到C点时,△PAD的面积最大,S△PAD=×AD×DC=8,∴AD=4,又∵S△ABD=×AB×AD=2,∴AB=1,∴当P点运动到BC中点时,△PAD的面积=×(AB+CD)×AD=5,故答案为:5.
18.答案见解析
【解析】试题分析:(1)观察图象,可知最高温度为37℃,时间为15时,最低温度是23℃,时间为3时;
(2)由(1)中得出的最高温度-最低温度即可求出温差,也可求得经过的时间;
(3)观察图象可求解.
试题解析:(1)根据图象可以看出:这一天的最高温度是37℃,是在15时到达的,最低温度是23℃,是在3时达到的;
(2)温差为:37 23=14(℃),经过的时间为:15 3=12(时);
(3)从3时到15时温度在上升,在0时到3时、15时到24时温度在下降.
19.(1) 自变量是时间,因变量是距离;(2) 10时他距家15千米,13时他距家30千米;
(3) 12:00时他到达离家最远的地方,离家30千米;(4)11千米;
(5) 12:00~13:00休息并吃午餐;(6) 15千米/时
【解析】解:(1)图象表示了时间、距离的关系,自变量是时间,因变量是距离. (2)由图象看出10时他距家15千米,13时他距家30千米. (3)由图象看出12:00时他到达离家最远的地方,离家30千米. (4)由图象看出11时距家19千米,12时距家30千米,11时到12时他行驶了30- 19=11(千米). (5)由图象看出12:00~13:00时距离没变且时间较长,得12:00~13:00休息并吃午餐. (6)由图象看出回家时用了2小时,路程是30千米,所以回家的平均速度是30÷2=15(千米/时).
20.(1)5小时(2)24(3)油箱中的油刚好够用.
【解析】试题分析:(1)根据图象可得,5小时时,机动车内的油从12升变为了36升,故5小时后加油;
(2)用36-12即可;
(3)首先计算出耗油量,再根据路程和速度计算出行驶240km的时间,然后用时间乘以耗油量可得所消耗的油,和油箱里的油量进行比较即可.
试题解析:(1)根据图象可直接得到:机动车行驶5小时后加油;
(2)36 12=24(L);
(3)够用,
耗油量:(42 12)÷5=6(km/L),240÷40=6(小时), 6×6=36(L),
故够用.
21.答案见解析
【解析】试题分析:(1)根据函数图象的横坐标,可得答案;
(2)根据自变量的值与函数值的对应关系,可得相应的函数值;
(3)根据函数值,可得相应自变量的值;
(4)根据函数图象的最高点、最低点,可得相应自变量的值;
(5)根据函数图象的横坐标,可得函数的增区间.
试题解析:(1)-4≤x≤4.
(2)y的值分别是2,-2,0.
(3)当y=0时,x的值是-3,-1或4;
当y=4时,x的值是1.5.
(4)当x=1.5时,y的值最大;
当x=-2时,y的值最小.
(5)当-2≤x≤1.5时,y随x的增大而增大;
当-4≤x≤-2和1.5≤x≤4时,y随x的增大而减小.
22.见解析
【解析】试题分析:
(1)(3)观察、分析图象中的数据信息,结合题意即可得到相应答案;
(4)图中的横线表示人的正常体温:37℃;
(5)由图象可知,这位病人的体温逐渐趋近于正常体温,由此可知病人的病情在好转.
试题解析:
(1)观察图象可得:护士每隔6小时给病人测量一次体温;
(2)观察图象可得:这位病人的最高体温是39.5℃,最低体温是36.8℃;
(3)这位病人4月8日12时的体温是37.5℃;
(4)图中的横线表示人的正常体温是37℃;
(5)从图象的变化趋势看可以看出,这位病人的体温逐渐趋近于正常体温,
∴这位病人的病情在好转.
23.()甲、乙两人工作了小时,完成的零件数相同,为个;()甲: 时, , 时, .乙: 时, , 时, ;()当甲、乙两人各自完成40个和95个零件的时候,甲比乙少用.
【解析】试题分析:(1)观察可知点C的实际意义是甲、乙都工件了5小时,完成的零件数相同;
(2)利用待定系数法分别分段进行求解即可;
(3)分时间段进行讨论即可得.
试题解析:()甲、乙两人工作了小时,完成的零件数相同,为个;
()甲: 时, ,
时, .
乙: 时, ,
时, ,
()①当,则, .
②当,则, .
③当时,甲比乙完成慢,不会出现甲比乙少用这种情况,
综上所述,当甲、乙两人各自完成40个和95个零件的时候,甲比乙少用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
