17.3.2 一次函数的图象同步练习
文档属性
| 名称 | 17.3.2 一次函数的图象同步练习 |

|
|
| 格式 | docx | ||
| 文件大小 | 503.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-01 20:31:16 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
17.3.2 一次函数的图象同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.一次函数y=kx+b(k≠0,k、b为常数)的图象是一条直线,通常称 直线 y=kx+b.一般地,画一次函数y=kx+b的图象只需过(0,b)和(,0)两点画直线即可.
2.正比例函数y=kx(k≠0)的图象是过原点的直线.一般取(0,0)和(1,k)两点.
3.直线的平移可转化为点的平移,直线在平移的过程中有其规律,可简化为:上加下减,左加右减.
基础知识和能力拓展精练
一、选择题
1.一次函数y=ax﹣a(a≠0)的大致图象是( )
A. B. C. D.
2.一次函数y=k(x-1)的图象经过点M(-1,-2),则其图象与y轴的交点是( )
A. (0,-1) B. (1,0) C. (0,0) D. (0,1)
3.若正比例函数的图象经过(﹣3,2),则这个图象一定经过点( )
A. (2,﹣3) B. (,-1) C. (﹣1,1) D. (2,﹣2)
4.设点是正比例函数图象上的任意一点,则下列等式一定成立的是( ).
A. B. C. D.
5.若式子+(k-1)0有意义,则一次函数y=(k-1)x+1-k的图象可能是( )
A. B. C. D.
6.(2017湖北省鄂州市梁子湖区联考)直线y=kx+b过点(2,2)且与直线y=-3x相交于点(1,a),则两直线与x轴所围成的面积为( )
A. 2 B. 2.4 C. 3 D. 4.8
7.如图,一次函数和(a≠0,b≠0)在同一坐标系的图象.则的解中( )
A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<0
8.如图,直线OA是某正比例函数的图象,下列各点在该函数图象上的是( )
A. (-4,16) B. (3,6) C. (-1,-1) D. (4,6)
9.已知点、是正比例函数图象上关于原点对称的两点,则的值为( ).
A. B. C. D.
10.在平面直角坐标系中,将直线l1:y=-2x-2平移后,得到直线l2:y=-2x+4,则下列平移方法正确的是( )
A. 将l1向右平移3个单位长度 B. 将l1向右平移6个单位长度
C. 将l1向上平移2 个单位长度 D. 将l1向上平移4个单位长度
二、填空题
11.一次函数y=﹣2x+6的图象与x轴交点坐标是______,与y轴交点坐标是______.
12.如图,直线y=-2x+2与x轴交于A点,与y轴交于B点.过点B作直线BP与x轴交于P点,若△ABP的面积是3,则P点的坐标是______
13.如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为____.
14.已知直线y=kx﹣4(k≠0)与两坐标轴所围成的三角形的面积为4,则该直线的函数关系式为________.
15.将一次函数的图象向上平移个单位后,当时, 的取值范围是_________.
三、解答题
16.如图,在平面直角坐标系中,直线 与轴交于点A,直线 与 轴交于点B,与直线y=2x+3交于点C(-1,n).
(1)求n、k的值;
(2)求△ABC的面积.
17.已知y与x-3成正比例,当x=4时,y=3.
(1) 求出y与x之间的函数关系式;
(2) y与x之间是什么函数关系? 并在平面直角坐标系中画出该函数的图像;
(3) 当x=2.5时,y的值为__________.
18.已知一次函数,求:
(1) m为何值时,函数图象与y轴的交点在轴下方?
(2) m为何值时,图象经过第一、三、四象限?
19.已知一次函数,回答下列问题:
(1)若次函数的图像过原点,求k的值;
(2)无论k取何值,该函数的图像总经过一个定点,请你求出这个定点的坐标。
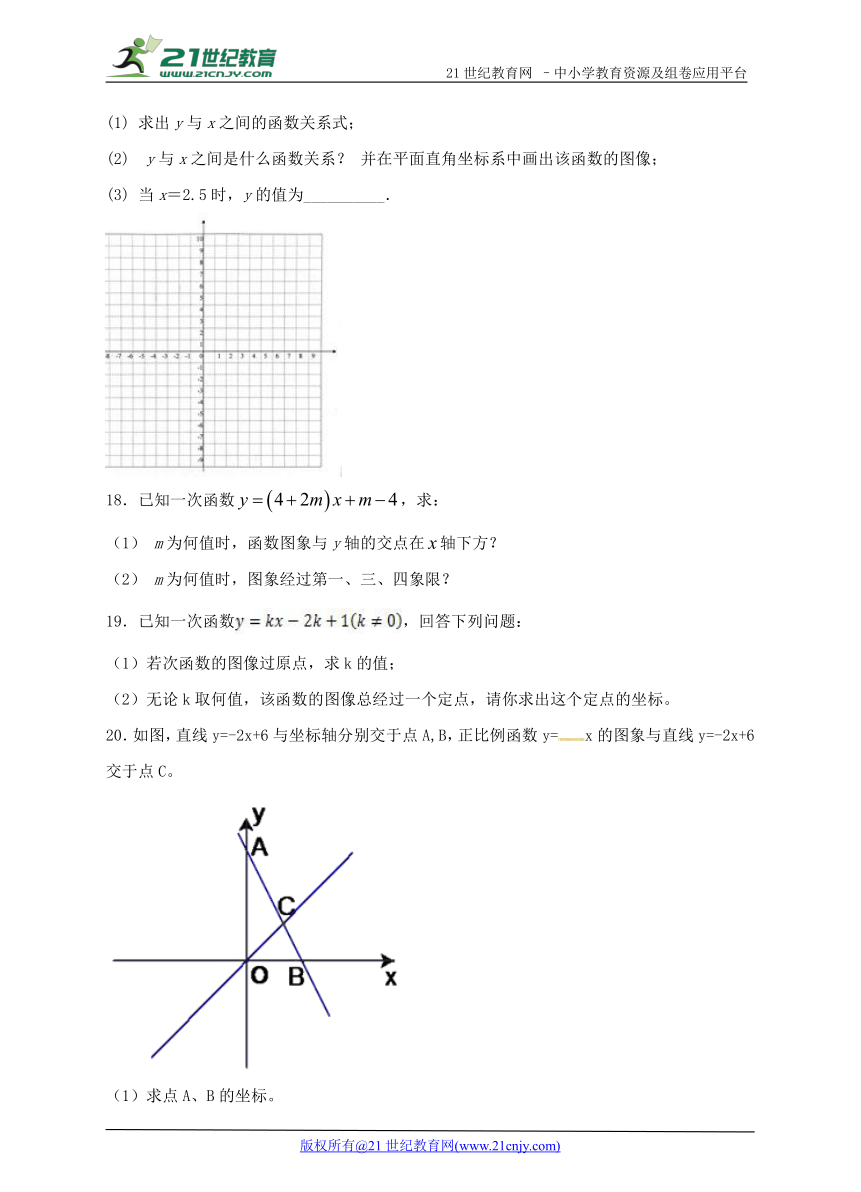
20.如图,直线y=-2x+6与坐标轴分别交于点A,B,正比例函数y=x的图象与直线y=-2x+6交于点C。
(1)求点A、B的坐标。
(2)求△BOC的面积
(3)已知点P是y轴上的一个动点,求BP+CP的最小值和此时点P的坐标。
参考答案
1.A
【解析】当a>0时,-a<0,一次函数y=ax-a经过第一、三、四象限,选项A符合;
当a<0时,-a>0,一次函数y=ax-a图象经过第一、二、四象限,无选项符合.
故选:A.
2.A
【解析】试题解析:把点M(-1,-2)代入一次函数y=k(x-1),
解得:
即
当时,
图象与y轴的交点是
故选A.
3.B
【解析】试题解析:设正比例函数的解析式为y=kx(k≠0),
∵正比例函数的图象经过(-3,2),
∴-3k=2,解得k=-,
∴正比例函数的解析式为:y=-x.
A、∵当x=2时,y=-×2=-≠-3,∴此点不在函数图象上,故本选项错误;
B、∵当x=时,y=-×=-1,∴此点在函数图象上,故本选项正确;
C、∵当x=-1时,y=-×(-1)=≠1,∴此点不在函数图象上,故本选项错误;
D、∵当x=2时,y=-×2=-≠-2,∴此点不在函数图象上,故本选项错误.
故选B.
4.D
【解析】试题解析:把点代入正比例函数,可得,所以, 选项正确.故选D.
5.B
【解析】∵式子+(k-1)0有意义,
∴ ,解得: ,
∴k-1>0,1-k<0,
∴一次函数y=(k-1)x+1-k的图象可能是B.
故选B.
6.B
【解析】试题解析:∵点(2,2)在直线y=-3x上, ∴a=-3,
又y=kx+b过点(2,2), (1,-3)
又y=kx+b过点(2,2), (1,-3)
∴,解得 ,
所以,直线为 y=5x-8,
令y=0 ,则5x-8=0 ,解得x=,
所以,与x 轴的交点坐标为(,0),
∵直线y=-3x经过坐标原点,
两直线与x轴所围成的面积=×3=2.4.
故选B .
7.A
【解析】试题解析::∵方程组的解即是一次函数y1=ax+b和y2=bx+a的交点坐标,
由图象可知,交点(m,n)在第一象限,
∴m>0,n>0.
故选A.
8.B
【解析】试题解析:设该正比例函数的解析式为y=kx(k≠0),
∵函数图象过点(2,4),
∴4=2k,解得k=2,
∴此函数的解析式为y=2x,
A、∵当x=-4时,y=2×(-4)=-8≠16,∴此点不在该函数的图象上,故本选项错误;
B、∵当x=3时,y=2×3=6,∴此点在该函数的图象上,故本选项正确;
C、∵当x=-1时,y=2×(-1)=-2≠-1,∴此点不在该函数的图象上,故本选项错误;
D、∵当x=4时,y=2×4=8≠6,∴此点不在该函数的图象上,故本选项错误.
故选B.
9.A
【解析】试题解析:∵, 关于原点对称,
∴, ,
把代入得,计算得出.
所以选项是正确的.
故选A
10.A
【解析】解:∵将直线l1:y=﹣2x﹣2平移后,得到直线l2:y=﹣2x+4,∴﹣2(x+a)﹣2=﹣2x+4,解得:a=﹣3,故将l1向右平移3个单位长度.故选A.
点睛:此题主要考查了一次函数图象与几何变换,正确把握变换规律是解题关键.
11. (3,0) (0,6)
【解析】根据一次函数和坐标轴的关系,可知当x=0时,y=6,可知与y轴的交点坐标为(0,6),当y=0时,可知与x轴的交点的坐标为:(3,0).
故答案为:(3,0),(0,6).
点睛:此题主要考查了一次函数的图像与性质,解题关键是明确直线与坐标轴的交点的特点,与x轴的交点y=0,与y轴的交点x=0,由此可代入求解,比较简单.
12.(4,0),(-2,0)
【解析】∵△ABP的面积为3,
∴OB AP=3
又∵OB=2,
∴AP=3
∴点P的坐标为(4,0),(-2,0).
故答案为:(4,0),(-2,0).
13.(,0)
【解析】试题分析:如图所示,作点B关于x轴对称的点B',连接AB',交x轴于P,则点P即为所求,
设直线y=-x沿y轴向下平移后的直线解析式为y=-x+a,
把A(2,-4)代入可得,a=-2,
∴平移后的直线为y=-x-2,
令x=0,则y=-2,即B(0,-2)
∴B'(0,2),
设直线AB'的解析式为y=kx+b,
把A(2,-4),B'(0,2)代入可得,
,
解得,
∴直线AB'的解析式为y=-3x+2,
令y=0,则x=,
∴P(,0),
故答案为:(,0).
点睛:本题属于最短路线问题,主要考查了一次函数图象与几何变换的运用,解决问题的关键是掌握:在直线l上的同侧有两个点A、B,在直线l上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线l的对称点,对称点与另一点的连线与直线l的交点就是所要找的点.
14.y=2x﹣4或y=﹣2x﹣4.
【解析】直线与y轴的交点坐标为(0,﹣4),与x轴的交点坐标为(,0),则与坐标轴围成的三角形的面积为×4×| |=4,
解得k=±2,
故函数解析式为y=2x﹣4或y=﹣2x﹣4,
故答案为:y=2x﹣4或y=﹣2x﹣4.
【点睛】本题主要考查了用待定系数法求一次函数的解析式,根据三角形面积公式及已知条件,列出方程,求出k的值,即得一次函数的解析式.
15.
【解析】将一次函数y=2x的图像向上平移2个单位后得到的是直线y=2x+2,当y>0时,即2x+2>0,解得x>-1,
故答案为:x>-1.
16.(1); (2)2.
【解析】试题分析:(1)将点C的坐标代入直线y=2x+3中即可求得n的值,再求得点C的坐标代入直线中,即可求得k的值;(2)由S△ABC=即可计算得出.
试题解析:
(1)∵点C(-1,n)在直线y=2x+3上,
∴n=1,
∴点C的坐标为(-1,1),
∵将点C(-1,1)在直线上,
∴-k-1=1
∴k=-2
(2).
17.(1) y=3x-9;(2) y是x的一次函数,该函数的图像见解析;(3) -1.5
【解析】试题分析:(1)根据y与x-3成正比例,设出一次函数的关系式,再把当x=4时,y=3代入求出k的值即可;
(2)根据一次函数的定义可得y与x之间的函数关系,再根据描点法画出函数即可求解;
(3)根据代入法即可求解.
试题解析:
(1)∵y与x-3成正比例,设出一次函数的关系式为:y=k(x-3)(k≠0),
把当x=4时,y=-3代入得:3=(4-3)k,解得k=3,
∴y与x之间的函数关系式为:y=3(x-3)=3x-9.
(2)y是x的一次函数,该函数的图象如图所示;
(3)当x=2.5时,y=3×2.5-9=-1.5.
18.(1)m<4且m≠;(2)<m<4.
【解析】试题分析:(1)根据图象与y轴的交点在x轴的下方列出关于m的不等式,求出m的取值范围即可;
(2)根据图象经过第一、三、四象限列出关于m的不等式组,求出m的取值范围即可.
试题解析:(1)当x=0时,y=m-4,所以函数图象与y轴交点的坐标为(0,m-4),
由函数图象与y轴交点在x轴下方,
∴m-4<0且 4+2m≠0,
所以m<4且m≠;
(2)由图象经过第一、三、四象限可得: ,
解得: <m<4.
【点睛】本题考查的是一次函数的性质,熟知一次函数的图象与系数的关系是解答此题的关键.
19.(1)k=;
(2)这个定点的坐标(2,1)
【解析】试题分析:(1)由一次函数图象经过原点,即可得出-2k+1=0,解之即可得出结论;
(2)由一次函数的解析式可得出(x-2)k=y-1,由“无论k取何值,该函数图象总经过一个定点”可得出x-2=0、y-1=0,解之即可得出该定点的坐标.
试题解析:(1)一次函数图象过原点,
∴-2k+1=0,
解得k=
(2)∵=k(x-2)+1,
∴(x-2)k=y-1 .
∵无论k取何值,该函数图象总经过一个定点,即k有无数个解,
∴x-2=0,y-1=0,
解得x=2,y=1,
∴这个定点的坐标(2,1)
20.(1)A(0,6) ,B(3,0);(2)3;(4),(0, ).
【解析】试题分析:令直线y=-2x+6中x、y分别为0,即可求得点A、B坐标;
(2)先了联立方程组,解得点C的坐标,再由三角形面积公式求得△BOC的面积;
(3)作点C关于y轴对称点,连接B,与y轴交点即为使BP+CP取得最小值的点P的坐标.
试题解析:(1)令x=0,得y=6,令y=0,得x=3,
所以A(0,6) ,B(3,0) ;
(2) ,解得
所以点C(2,2),
;
(3)作点C关于y轴对称点,
BP+CP的最小值= =
直线的函数表达式
直线与y 轴交点即为点P(0, )
点睛:此题是一次函数综合题,主要考查直线的交点坐标的求法,三角形的面积公式,最短路径问题.解题的关键是掌握联立两直线的解析式求两直线的交点坐标的方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
17.3.2 一次函数的图象同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.一次函数y=kx+b(k≠0,k、b为常数)的图象是一条直线,通常称 直线 y=kx+b.一般地,画一次函数y=kx+b的图象只需过(0,b)和(,0)两点画直线即可.
2.正比例函数y=kx(k≠0)的图象是过原点的直线.一般取(0,0)和(1,k)两点.
3.直线的平移可转化为点的平移,直线在平移的过程中有其规律,可简化为:上加下减,左加右减.
基础知识和能力拓展精练
一、选择题
1.一次函数y=ax﹣a(a≠0)的大致图象是( )
A. B. C. D.
2.一次函数y=k(x-1)的图象经过点M(-1,-2),则其图象与y轴的交点是( )
A. (0,-1) B. (1,0) C. (0,0) D. (0,1)
3.若正比例函数的图象经过(﹣3,2),则这个图象一定经过点( )
A. (2,﹣3) B. (,-1) C. (﹣1,1) D. (2,﹣2)
4.设点是正比例函数图象上的任意一点,则下列等式一定成立的是( ).
A. B. C. D.
5.若式子+(k-1)0有意义,则一次函数y=(k-1)x+1-k的图象可能是( )
A. B. C. D.
6.(2017湖北省鄂州市梁子湖区联考)直线y=kx+b过点(2,2)且与直线y=-3x相交于点(1,a),则两直线与x轴所围成的面积为( )
A. 2 B. 2.4 C. 3 D. 4.8
7.如图,一次函数和(a≠0,b≠0)在同一坐标系的图象.则的解中( )
A. m>0,n>0 B. m>0,n<0 C. m<0,n>0 D. m<0,n<0
8.如图,直线OA是某正比例函数的图象,下列各点在该函数图象上的是( )
A. (-4,16) B. (3,6) C. (-1,-1) D. (4,6)
9.已知点、是正比例函数图象上关于原点对称的两点,则的值为( ).
A. B. C. D.
10.在平面直角坐标系中,将直线l1:y=-2x-2平移后,得到直线l2:y=-2x+4,则下列平移方法正确的是( )
A. 将l1向右平移3个单位长度 B. 将l1向右平移6个单位长度
C. 将l1向上平移2 个单位长度 D. 将l1向上平移4个单位长度
二、填空题
11.一次函数y=﹣2x+6的图象与x轴交点坐标是______,与y轴交点坐标是______.
12.如图,直线y=-2x+2与x轴交于A点,与y轴交于B点.过点B作直线BP与x轴交于P点,若△ABP的面积是3,则P点的坐标是______
13.如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为____.
14.已知直线y=kx﹣4(k≠0)与两坐标轴所围成的三角形的面积为4,则该直线的函数关系式为________.
15.将一次函数的图象向上平移个单位后,当时, 的取值范围是_________.
三、解答题
16.如图,在平面直角坐标系中,直线 与轴交于点A,直线 与 轴交于点B,与直线y=2x+3交于点C(-1,n).
(1)求n、k的值;
(2)求△ABC的面积.
17.已知y与x-3成正比例,当x=4时,y=3.
(1) 求出y与x之间的函数关系式;
(2) y与x之间是什么函数关系? 并在平面直角坐标系中画出该函数的图像;
(3) 当x=2.5时,y的值为__________.
18.已知一次函数,求:
(1) m为何值时,函数图象与y轴的交点在轴下方?
(2) m为何值时,图象经过第一、三、四象限?
19.已知一次函数,回答下列问题:
(1)若次函数的图像过原点,求k的值;
(2)无论k取何值,该函数的图像总经过一个定点,请你求出这个定点的坐标。
20.如图,直线y=-2x+6与坐标轴分别交于点A,B,正比例函数y=x的图象与直线y=-2x+6交于点C。
(1)求点A、B的坐标。
(2)求△BOC的面积
(3)已知点P是y轴上的一个动点,求BP+CP的最小值和此时点P的坐标。
参考答案
1.A
【解析】当a>0时,-a<0,一次函数y=ax-a经过第一、三、四象限,选项A符合;
当a<0时,-a>0,一次函数y=ax-a图象经过第一、二、四象限,无选项符合.
故选:A.
2.A
【解析】试题解析:把点M(-1,-2)代入一次函数y=k(x-1),
解得:
即
当时,
图象与y轴的交点是
故选A.
3.B
【解析】试题解析:设正比例函数的解析式为y=kx(k≠0),
∵正比例函数的图象经过(-3,2),
∴-3k=2,解得k=-,
∴正比例函数的解析式为:y=-x.
A、∵当x=2时,y=-×2=-≠-3,∴此点不在函数图象上,故本选项错误;
B、∵当x=时,y=-×=-1,∴此点在函数图象上,故本选项正确;
C、∵当x=-1时,y=-×(-1)=≠1,∴此点不在函数图象上,故本选项错误;
D、∵当x=2时,y=-×2=-≠-2,∴此点不在函数图象上,故本选项错误.
故选B.
4.D
【解析】试题解析:把点代入正比例函数,可得,所以, 选项正确.故选D.
5.B
【解析】∵式子+(k-1)0有意义,
∴ ,解得: ,
∴k-1>0,1-k<0,
∴一次函数y=(k-1)x+1-k的图象可能是B.
故选B.
6.B
【解析】试题解析:∵点(2,2)在直线y=-3x上, ∴a=-3,
又y=kx+b过点(2,2), (1,-3)
又y=kx+b过点(2,2), (1,-3)
∴,解得 ,
所以,直线为 y=5x-8,
令y=0 ,则5x-8=0 ,解得x=,
所以,与x 轴的交点坐标为(,0),
∵直线y=-3x经过坐标原点,
两直线与x轴所围成的面积=×3=2.4.
故选B .
7.A
【解析】试题解析::∵方程组的解即是一次函数y1=ax+b和y2=bx+a的交点坐标,
由图象可知,交点(m,n)在第一象限,
∴m>0,n>0.
故选A.
8.B
【解析】试题解析:设该正比例函数的解析式为y=kx(k≠0),
∵函数图象过点(2,4),
∴4=2k,解得k=2,
∴此函数的解析式为y=2x,
A、∵当x=-4时,y=2×(-4)=-8≠16,∴此点不在该函数的图象上,故本选项错误;
B、∵当x=3时,y=2×3=6,∴此点在该函数的图象上,故本选项正确;
C、∵当x=-1时,y=2×(-1)=-2≠-1,∴此点不在该函数的图象上,故本选项错误;
D、∵当x=4时,y=2×4=8≠6,∴此点不在该函数的图象上,故本选项错误.
故选B.
9.A
【解析】试题解析:∵, 关于原点对称,
∴, ,
把代入得,计算得出.
所以选项是正确的.
故选A
10.A
【解析】解:∵将直线l1:y=﹣2x﹣2平移后,得到直线l2:y=﹣2x+4,∴﹣2(x+a)﹣2=﹣2x+4,解得:a=﹣3,故将l1向右平移3个单位长度.故选A.
点睛:此题主要考查了一次函数图象与几何变换,正确把握变换规律是解题关键.
11. (3,0) (0,6)
【解析】根据一次函数和坐标轴的关系,可知当x=0时,y=6,可知与y轴的交点坐标为(0,6),当y=0时,可知与x轴的交点的坐标为:(3,0).
故答案为:(3,0),(0,6).
点睛:此题主要考查了一次函数的图像与性质,解题关键是明确直线与坐标轴的交点的特点,与x轴的交点y=0,与y轴的交点x=0,由此可代入求解,比较简单.
12.(4,0),(-2,0)
【解析】∵△ABP的面积为3,
∴OB AP=3
又∵OB=2,
∴AP=3
∴点P的坐标为(4,0),(-2,0).
故答案为:(4,0),(-2,0).
13.(,0)
【解析】试题分析:如图所示,作点B关于x轴对称的点B',连接AB',交x轴于P,则点P即为所求,
设直线y=-x沿y轴向下平移后的直线解析式为y=-x+a,
把A(2,-4)代入可得,a=-2,
∴平移后的直线为y=-x-2,
令x=0,则y=-2,即B(0,-2)
∴B'(0,2),
设直线AB'的解析式为y=kx+b,
把A(2,-4),B'(0,2)代入可得,
,
解得,
∴直线AB'的解析式为y=-3x+2,
令y=0,则x=,
∴P(,0),
故答案为:(,0).
点睛:本题属于最短路线问题,主要考查了一次函数图象与几何变换的运用,解决问题的关键是掌握:在直线l上的同侧有两个点A、B,在直线l上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线l的对称点,对称点与另一点的连线与直线l的交点就是所要找的点.
14.y=2x﹣4或y=﹣2x﹣4.
【解析】直线与y轴的交点坐标为(0,﹣4),与x轴的交点坐标为(,0),则与坐标轴围成的三角形的面积为×4×| |=4,
解得k=±2,
故函数解析式为y=2x﹣4或y=﹣2x﹣4,
故答案为:y=2x﹣4或y=﹣2x﹣4.
【点睛】本题主要考查了用待定系数法求一次函数的解析式,根据三角形面积公式及已知条件,列出方程,求出k的值,即得一次函数的解析式.
15.
【解析】将一次函数y=2x的图像向上平移2个单位后得到的是直线y=2x+2,当y>0时,即2x+2>0,解得x>-1,
故答案为:x>-1.
16.(1); (2)2.
【解析】试题分析:(1)将点C的坐标代入直线y=2x+3中即可求得n的值,再求得点C的坐标代入直线中,即可求得k的值;(2)由S△ABC=即可计算得出.
试题解析:
(1)∵点C(-1,n)在直线y=2x+3上,
∴n=1,
∴点C的坐标为(-1,1),
∵将点C(-1,1)在直线上,
∴-k-1=1
∴k=-2
(2).
17.(1) y=3x-9;(2) y是x的一次函数,该函数的图像见解析;(3) -1.5
【解析】试题分析:(1)根据y与x-3成正比例,设出一次函数的关系式,再把当x=4时,y=3代入求出k的值即可;
(2)根据一次函数的定义可得y与x之间的函数关系,再根据描点法画出函数即可求解;
(3)根据代入法即可求解.
试题解析:
(1)∵y与x-3成正比例,设出一次函数的关系式为:y=k(x-3)(k≠0),
把当x=4时,y=-3代入得:3=(4-3)k,解得k=3,
∴y与x之间的函数关系式为:y=3(x-3)=3x-9.
(2)y是x的一次函数,该函数的图象如图所示;
(3)当x=2.5时,y=3×2.5-9=-1.5.
18.(1)m<4且m≠;(2)<m<4.
【解析】试题分析:(1)根据图象与y轴的交点在x轴的下方列出关于m的不等式,求出m的取值范围即可;
(2)根据图象经过第一、三、四象限列出关于m的不等式组,求出m的取值范围即可.
试题解析:(1)当x=0时,y=m-4,所以函数图象与y轴交点的坐标为(0,m-4),
由函数图象与y轴交点在x轴下方,
∴m-4<0且 4+2m≠0,
所以m<4且m≠;
(2)由图象经过第一、三、四象限可得: ,
解得: <m<4.
【点睛】本题考查的是一次函数的性质,熟知一次函数的图象与系数的关系是解答此题的关键.
19.(1)k=;
(2)这个定点的坐标(2,1)
【解析】试题分析:(1)由一次函数图象经过原点,即可得出-2k+1=0,解之即可得出结论;
(2)由一次函数的解析式可得出(x-2)k=y-1,由“无论k取何值,该函数图象总经过一个定点”可得出x-2=0、y-1=0,解之即可得出该定点的坐标.
试题解析:(1)一次函数图象过原点,
∴-2k+1=0,
解得k=
(2)∵=k(x-2)+1,
∴(x-2)k=y-1 .
∵无论k取何值,该函数图象总经过一个定点,即k有无数个解,
∴x-2=0,y-1=0,
解得x=2,y=1,
∴这个定点的坐标(2,1)
20.(1)A(0,6) ,B(3,0);(2)3;(4),(0, ).
【解析】试题分析:令直线y=-2x+6中x、y分别为0,即可求得点A、B坐标;
(2)先了联立方程组,解得点C的坐标,再由三角形面积公式求得△BOC的面积;
(3)作点C关于y轴对称点,连接B,与y轴交点即为使BP+CP取得最小值的点P的坐标.
试题解析:(1)令x=0,得y=6,令y=0,得x=3,
所以A(0,6) ,B(3,0) ;
(2) ,解得
所以点C(2,2),
;
(3)作点C关于y轴对称点,
BP+CP的最小值= =
直线的函数表达式
直线与y 轴交点即为点P(0, )
点睛:此题是一次函数综合题,主要考查直线的交点坐标的求法,三角形的面积公式,最短路径问题.解题的关键是掌握联立两直线的解析式求两直线的交点坐标的方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
