第17章 函数及其图像单元检测提高卷
文档属性
| 名称 | 第17章 函数及其图像单元检测提高卷 |

|
|
| 格式 | doc | ||
| 文件大小 | 814.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-02 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第17章函数及其图像单元检测提高卷
班级__________姓名____________总分___________
一、选择题
1.在平面直角坐标系中,点P(m+1,2﹣m)在第二象限,则m的取值范围为( )
A. m<﹣1 B. m<2 C. m>2 D. ﹣1<m<2
2.已知点在第二象限,若点到轴的距离与到轴的距离之和是6,则的值为( )
A. 1 B. C. 5 D. 3
3.函数的自变量x的取值范围为( )
A. x≠1 B. x>-1 C. x≥-1 D. x≥-1且 x≠1
4.如表列出了一项实验的统计数据:
它表示皮球从一定高度落下时,下落高度y与弹跳高度x的关系,能表示变量y与x之间的关系式为( )
A. y=2x-10 B. y= C. y=x+25 D. y=x+5
5.已知点P(m,n)是一次函数y=x﹣1的图象位于第一象限部分上的点,其中实数m、n满足,则点P的坐标为( )
A. (,) B. (,) C. (2,1) D. (,)
6.已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
7.直线y=(3-π)x经过的象限是( )
A. 一、二象限 B. 一、三象限 C. 二、三象限 D. 二、四象限
8.根据如图的程序,计算当输入值x=﹣2时,输出结果y为( )
A. 1 B. 5 C. 7 D. 以上都有可能
9.(2017湖南怀化第8题)一次函数的图象经过点,且与轴、轴分别交于点、,则的面积是( )
A. B. C. 4 D. 8
10.如图,直线y=﹣x+m与y=nx+4n的交点的横坐标为﹣2,则关于x的不等式nx+4n>﹣x+m>0的整数解可能是( )
A. 1 B. ﹣1 C. ﹣2 D. ﹣3
二、填空题
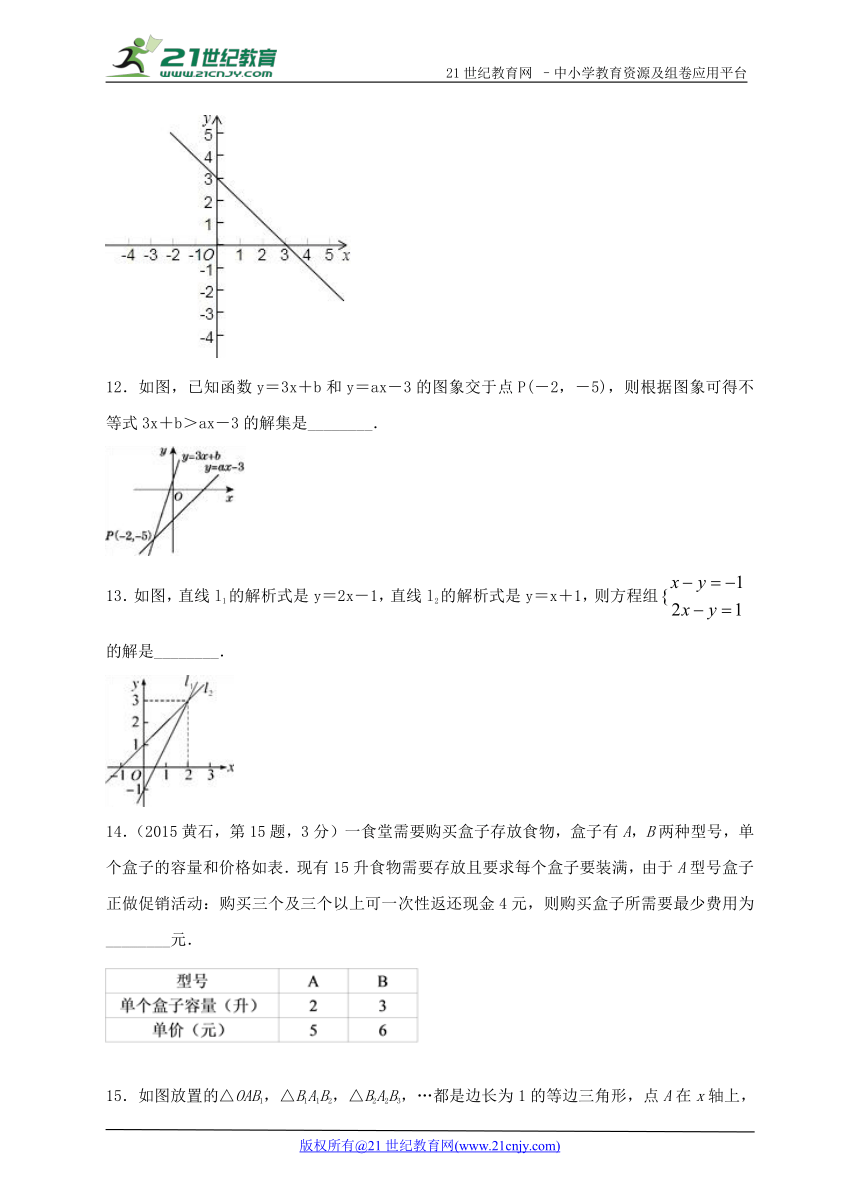
11.如图,已知一次函数y=﹣x+3 当x________时,y=﹣2;
当x________时,y<﹣2;
当x________时,y>﹣2;
当﹣3<y<3时,x的取值范围是________.
12.如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是________.
13.如图,直线l1的解析式是y=2x-1,直线l2的解析式是y=x+1,则方程组的解是________.
14.(2015黄石,第15题,3分)一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为________元.
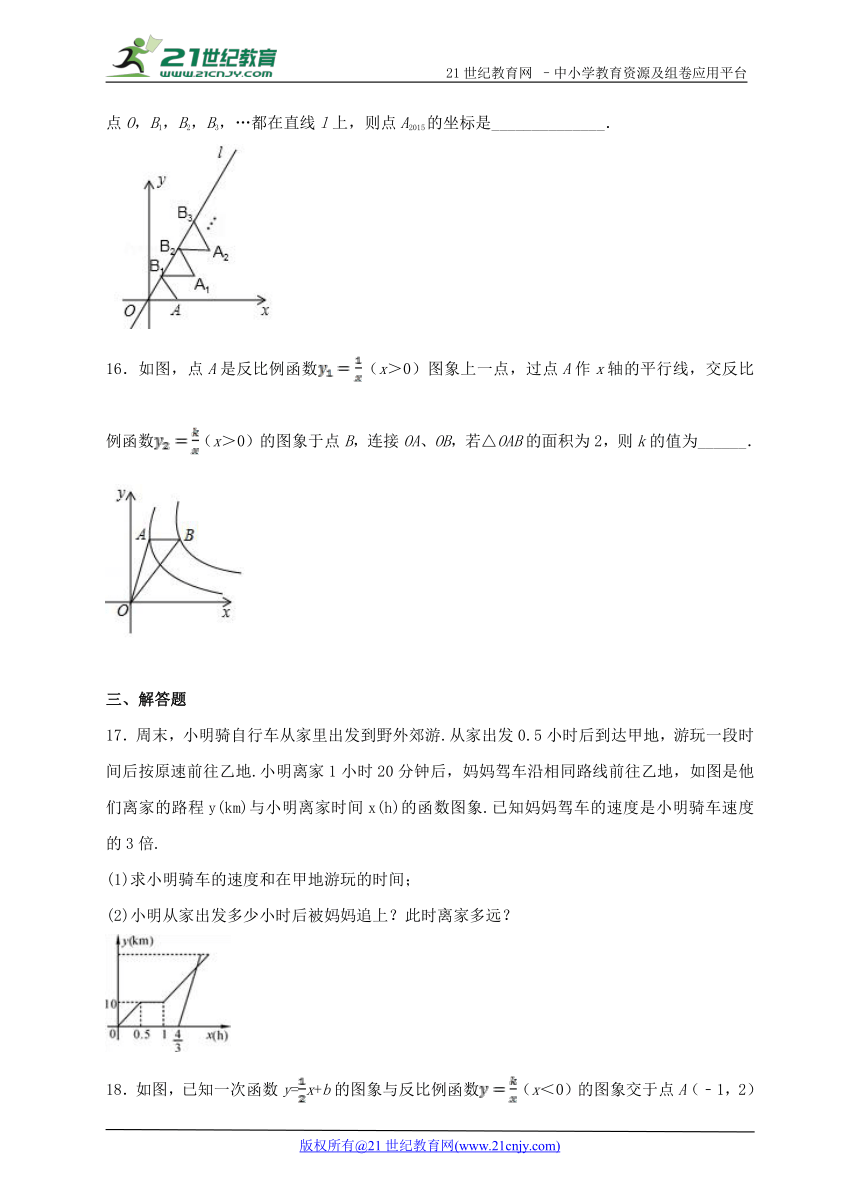
15.如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是______________.
16.如图,点A是反比例函数(x>0)图象上一点,过点A作x轴的平行线,交反比例函数(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为______.
三、解答题
17.周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
18.如图,已知一次函数y=x+b的图象与反比例函数(x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当时,请直接写出x的取值范围.
19.已知点A(a,0)、B(b,0),且 +|b﹣2|=0.
(1)求a、b的值.
(2)在y轴的正半轴上找一点C,使得三角形ABC的面积是15,求出点C的坐标.
(3)过(2)中的点C作直线MN∥x轴,在直线MN上是否存在点D,使得三角形ACD的面积是三角形ABC面积的?若存在,求出点D的坐标;若不存在,请说明理由.
20.已知一次函数 EMBED Equation.DSMT4 的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为、.
(1)当P为线段AB的中点时,求的值;
(2)直接写出的范围,并求当时点P的坐标;
(3)若在线段AB上存在无数个P点,使(a为常数),求a的值.
21.如图,已知A( 4,2)、B(a, 4)是一次函数y=kx+b的图象与反比例函数 EMBED Equation.DSMT4 的图象的两个交点;
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
22.如图,直线l是一次函数y=kx+b的图象,点A、B在直线l上.根据图象回答下列问题:
(1)写出方程kx+b=0的解;
(2)写出不等式kx+b>1的解集;
(3)若直线l上的点P(m,n)在线段AB上移动,则m、n应如何取值.
23.(2017湖南省长沙市,第24题,9分)自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该欧洲客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件.已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出.设购进A型商品m件,求该客商销售这批商品的利润v与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,欧洲客商决定在试销活动中每售出一件A型商品,就从一件A型商品的利润中捐献慈善资金a元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.
24.如图,P1、P2是反比例函数(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(1)求反比例函数的解析式.
(2)①求P2的坐标.
②根据图象直接写出在第一象限内当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数的函数值.
25.如图,直线y=2x+m(m>0) 与x轴交于点A(-2,0) (, ),直线与轴、轴分别交于、两点,并与直线相交于点,若.
(1)求点的坐标;
(2)求出四边形的面积;
(3)若为轴上一点,且为等腰三角形,直接写出点的坐标.
26.如图,在平面直角坐标系xoy中,函数(x<0)的图象与直线y=x+2交于点A(-3,m).
(1)求k,m的值;
(2)已知点P(a,b)是直线y=x上,位于第三象限的点,过点P作平行于x轴的直线,交直线y=x+2于点M,过点P作平行于y轴的直线,交函数(x<0)的图象于点N.
①当a=-1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM结合函数的图象,直接写出b的取值范围.
参考答案
1.A
【解析】根据题意,得:,解得m<﹣1,
故选A.
2.B
【解析】根据题意,先由点P(2a,1-3a)在第二象限,可知2a<0,1-3a>0,求得a<0,a<,可得a的取值范围:a<0,然后由点P到x轴的距离与到y轴的距离之和为6,可得|2a|+|1-3a|=6,即-2a+1-3a=6,解得a=-1,
故选:B.
点睛:本题考查的知识点为:第二象限点的符号为(-,+);负数的绝对值为它的相反数;正数的绝对值为它本身.
3.A
【解析】试题解析:根据题意得: x-1≠0,
解得: x≠1.
故选A.
4.A
【解析】根据题意,设函数关系式为y=kx+b,
则
解得: ,
则y=2x-10.
故选:A.
5.D
【解析】解:∵,化简,得(m+n)2=4,∵点P(m,n)是一次函数y=x﹣1的图象位于第一象限部分上的点,∴n=m﹣1,∴,解得:或.
∵点P(m,n)是一次函数y=x﹣1的图象位于第一象限部分上的点,∴m>0,n>0,故点P的坐标为(1.5,0.5),故选D.
6.A
【解析】试题解析:∵k+b=﹣5,kb=6,∴k<0,b<0识.
∴根据一次函数图象与系数的关系:
①当k>0,b>0时,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0时,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
∴直线y=kx+b经过二、三、四象限,不经过第一象限.
故选A.
7.D
【解析】由题意得: ,则直线经过. 二、四象限.故选D.
8.C
【解析】先由x=﹣2≤﹣1,确定x与y的关系式为y=x2+3,然后代值计算即可.
解:∵x=﹣2≤﹣1,
∴y=x2+3=(﹣2)2+3=7,
故选C.
9.B
【解析】试题解析:∵一次函数y=﹣2x+m的图象经过点P(﹣2,3),
∴3=4+m,
解得m=﹣1,
∴y=﹣2x﹣1,
∵当x=0时,y=﹣1,
∴与y轴交点B(0,﹣1),
∵当y=0时,x=﹣,
∴与x轴交点A(﹣,0),
∴△AOB的面积:V×1×=.
故选B.
10.B
【解析】∵直线y= x+m与y=nx+4n的交点的横坐标为 2,
∴关于x的不等式nx+4n>﹣x+m>0的解集为 2< x<0,
∴整数解可能是 1.
故选:B.
11. =5 >5 <5 0<x<6
【解析】如图,
当x=5时,y= 2;
当x>5时,y< 2;
当x<5时,y> 2;
当0故答案为:=5;>5;<5;0点睛:本题考查了一次函数与一元一次不等式:从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
12.x>-2
【解析】试题解析:从图象得到,当x>-2时,y=3x+b的图象对应的点在函数y=ax-3的图象上面,
∴不等式3x+b>ax-3的解集为:x>-2.
13.
【解析】试题分析:以二元一次方程组的两个方程画出的两个一次函数图像的交点就是二元一次方程组的解,本题中的交点坐标为(2,3),则方程组的解为: .
14.29.
【解析】解:设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为个。
①当0≤x<3时,=,∵k=1>0,∴y随x的增大而增大,∴当x=0时,y有最小值,最小值为30元;
②当时,=,∵k=1>0,∴y随x的增大而增大,∴当x=3时,y有最小值,最小值为29元;
综合①②可得,购买盒子所需要最少费用为29元.故答案为:29.
15.(,).
【解析】解:过B1向x轴作垂线B1C,垂足为C,由题意可得:A(1,0),AO∥A1B1,∠B1OC=30°,∴CB1=OB1cos30°=,∴B1的横坐标为:,则B1的纵坐标为:,∴点B1,B2,B3,…都在直线上,∴B1(,),等边三角形的边长为1可得出:A的横坐标为:1,∴y=,∴A2(2,),…
An(,).∴A2015(,).故答案为:(,).
16.5.
【解析】解:延长BA,与y轴交于点C.∵AB∥x轴,∴BC⊥y轴.∵A是反比例函数(x>0)图象上一点,B为反比例函数(x>0)的图象上的点,∴S△AOC=,S△BOC=.∵S△AOB=2,即=2,解得:k=5.故答案为:5.
17.(1)0.5 h.(2)1.75h,25km
【解析】试题分析:(1)用路程除以时间即可得到速度;在甲地游玩的时间是1-0.5=0.5小时;
(2)先求出妈妈驾车的速度,设妈妈从出发到追上小明的时间为t小时,根据妈妈追上小明时两人所走过的路程相等,列方程进行求解即可得.
试题解析:(1)小明骑车速度: =20(km/h),在甲地游玩的时间是1-0.5=0.5 h.
(2)妈妈驾车速度:20×3=60(km/h),
设妈妈从出发到追上小明的时间为t(h),由题意得20(t+)=60t,解得t= ,
所以小明出发+=1.75(h)后被妈妈追上,此时离家×60=25(km).
18.(1)C(0,);(2)x<﹣4或﹣1<x<0.
【解析】试题分析:(1)作点A关于y轴的对称点A′,连接A′B交y轴于点C,此时点C即是所求.由点A为一次函数与反比例函数的交点,利用待定系数法和反比例函数图象点的坐标特征即可求出一次函数与反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点A、B的坐标,再根据点A′与点A关于y轴对称,求出点A′的坐标,设出直线A′B的解析式为y=mx+n,结合点的坐标利用待定系数法即可求出直线A′B的解析式,令直线A′B解析式中x为0,求出y的值,即可得出结论;
(2)根据两函数图象的上下关系结合点A、B的坐标,即可得出不等式的解集.
试题解析:解:(1)作点A关于y轴的对称点A′,连接A′B交y轴于点C,此时点C即是所求,如图所示.
∵反比例函数(x<0)的图象过点A(﹣1,2),∴k=﹣1×2=﹣2,∴反比例函数解析式为(x<0);
∵一次函数y=x+b的图象过点A(﹣1,2),∴2=﹣+b,解得:b=,∴一次函数解析式为.联立一次函数解析式与反比例函数解析式成方程组:,解得:,或,∴点A的坐标为(﹣1,2)、点B的坐标为(﹣4,).
∵点A′与点A关于y轴对称,∴点A′的坐标为(1,2),设直线A′B的解析式为y=mx+n,则有,解得:,∴直线A′B的解析式为.令中x=0,则y=,∴点C的坐标为(0,).
(2)观察函数图象,发现:当x<﹣4或﹣1<x<0时,一次函数图象在反比例函数图象下方,∴当时,x的取值范围为x<﹣4或﹣1<x<0.
19.(1)a=﹣4,b=2;(2)C(0,5);(3)D(3,5)或(﹣3,5).
【解析】试题分析:(1)根据非负数的性质列方程,解方程即可得到结论;
(2)由A(﹣4,0)、B(2,0),得到AB=6,根据三角形ABC的面积是15,列方程求解即可得到结论;
(3)根据三角形ABC的面积是15列方程,解方程即可得到结论.
试题解析:解:(1)∵(a+4)2+|b﹣2|=0,∴a+4=0,b﹣2=0,∴a=﹣4,b=2;
(2)如图1,∵A(﹣4,0)、B(2,0),∴AB=6,∵三角形ABC的面积是15,∴ AB OC=15,∴OC=5,∴C(0,5);
(3)存在,如图2,∵三角形ABC的面积是15,∴S△ACD=CD OC=×15,∴CD×5=×15,∴CD=3,∴D(3,5)或(﹣3,5).
点睛:本题考查了坐标与图形的性质,非负数的性质,三角形的面积,正确作出图形是解题的关键.
20.(1)3;(2), P的坐标为(1,2)或(, );(3)2.
【解析】试题分析:(1)对于一次函数解析式,求出A与B的坐标,即可求出P为线段AB的中点时的值;
(2)根据题意确定出的范围,设P(m,2m﹣4),表示出,分类讨论m的范围,根据求出m的值,即可确定出P的坐标;
(3)设P(m,2m﹣4),表示出与,由P在线段上求出m的范围,利用绝对值的代数意义表示出与,代入,根据存在无数个点P求出a的值即可.
试题解析:解:(1)对于一次函数,令x=0,得到y=﹣4;令y=0,得到x=2,∴A(2,0),B(0,﹣4),∵P为AB的中点,∴P(1,﹣2),则;
(2)①;
②设P(m,2m﹣4),∴=,当0≤m≤2时, =m+4﹣2m=4﹣m=3,解得:m=1,此时P1(1,﹣2);
当m>2时, =m+2m﹣4=3,解得:m=,此时P2(, );
当m<0时,不存在,综上,P的坐标为(1,﹣2)或(, );
(3)设P(m,2m﹣4),∴=, =,∵P在线段AB上,∴0≤m≤2,∴=4﹣2m, =m,∵,∴4﹣2m+am=4,即(a﹣2)m=0,∵有无数个点,∴a=2.
21.(1)反比例函数的解析式为,一次函数的解析式为y=-x-2(2)-42
【解析】试题分析:(1)把A点坐标代入反比例函数解析式求出m的值,再把B点坐标代入反比例函数解析式求出a的值,从而得出点B的坐标,根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)由两函数图象的上下位置关系结合交点的横坐标,即可得出使一次函数值小于反比例函数值的x的取值范围.
试题解析:
解:(1)∵m=xy=(-4)×2=-8,
∴反比例函数的解析式为y=.
∴-4a=-8,
∴a=2,
y=kx+b过A(-4,2),B(2,-4)两点,
∴,
解得.
故一次函数的解析式为y=-x-2;
(2)观察函数图象可知:当-4<x<0或x>2时,一次函数图象在反比例函数图象下方,
∴一次函数的值小于反比例函数值的x的取值范围:-4<x<0或x>2.
点睛:本题考查了待定系数法求反比例函数和一次函数解析式、反比例函数与一次函数图象上点的坐标特征,解题的关键是:(1)根据点的坐标利用待定系数法求反比例函数和一次函数解析式;(2)根据两函数图象的上下位置关系找出使一次函数的值小于反比例函数的值的x的取值范围.
22.(1)x=-2;(2)x>0;(3)0≤n≤2
【解析】试题分析:从图象上得到函数的增减性及与坐标轴的交点的坐标后,解答各题.
试题解析:(1)函数经过点(-2,0),则方程的根是
答:
(2)函数经过点(0,1),则当时,有
即不等式的解集是
答
(3)线段的自变量的取值范围是:
当时,函数值的范围是
则.
答:
23.(1)一件B型商品的进价为150元,一件A型商品的进价为160元;(2)v=10m+17500(80≤m≤125);(3)当a<10时,最大利润为(18750﹣125a)元;当a=10时,最大利润为17500元;当a>10时,最大利润为(18300﹣80a)元.
【解析】试题分析:(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+10)元.根据16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,列出方程即可解决问题;
(2)根据总利润=两种商品的利润之和,列出式子即可解决问题;
(3)设利润为w元.则w=(80﹣a)m+70(250﹣m)=(10﹣a)m+17500,分三种情形讨论即可解决问题.
试题解析:解:(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+10)元.
由题意:,解得x=150,经检验x=150是分式方程的解.
答:一件B型商品的进价为150元,一件A型商品的进价为160元.
(2)因为客商购进A型商品m件,所以客商购进B型商品(250﹣m)件.
由题意:v=80m+70(250﹣m)=10m+17500,∵80≤m≤250﹣m,∴80≤m≤125,∴v=10m+17500(80≤m≤125);
(3)设利润为w元.则w=(80﹣a)m+70(250﹣m)=(10﹣a)m+17500:
①当10﹣a>0时,w随m的增大而增大,所以m=125时,最大利润为(18750﹣125a)元.
②当10﹣a=0时,最大利润为17500元.
③当10﹣a<0时,w随m的增大而减小,所以m=80时,最大利润为(18300﹣80a)元,∴当a<10时,最大利润为(18750﹣125a)元;当a=10时,最大利润为17500元;当a>10时,最大利润为(18300﹣80a)元.
点睛:本题考查了分式方程的应用、一次函数的应用等知识,解题的关键是理解题意,学会构建方程或一次函数解决问题,属于中考常考题型.
24.(1);(2)①P2(,);②2<x<.
【解析】试题分析:(1)先根据点A1的坐标为(4,0),△P1OA1为等腰直角三角形,求得P1的坐标,再代入反比例函数求解;(2)先根据△P2A1A2为等腰直角三角形,将P2的坐标设为(4+a,a),并代入反比例函数求得a的值,得到P2的坐标;再根据P1的横坐标和P2的横坐标,判断x的取值范围.
试题解析:解:(1)过点P1作P1B⊥x轴,垂足为B.∵点A1的坐标为(4,0),△P1OA1为等腰直角三角形,∴OB=2,P1B=OA1=2,∴P1的坐标为(2,2).将P1的坐标代入反比例函数(k>0),得k=2×2=4,∴反比例函数的解析式为;
(2)①过点P2作P2C⊥x轴,垂足为C.∵△P2A1A2为等腰直角三角形,∴P2C=A1C.设P2C=A1C=a,则P2的坐标为(4+a,a),将P2的坐标代入反比例函数的解析式为,得:,解得a1=,a2=(舍去),∴P2的坐标为(,);
②在第一象限内,当2<x<时,一次函数的函数值大于反比例函数的值.
25.(1)D点坐标为(, );(2);(3)点E的坐标为(2-2,0)、(-2-2,0)、(2,0)、(0,0).
【解析】(1)先把A点坐标代入y=2x+m得到m=4,则y=-2x+4,再利用AB=4可得到B点坐标为(2,0),则把B点坐标代入y=-x+n可得到n=2,则y=-x+2,然后根据两直线相交的问题,通过解方程组得到D点坐标;
(2)先确定C点坐标为(0,2),然后利用四边形AOCD的面积=S△DAB-S△COB进行计算即可;
(3)先利用A、C两点的坐标特征得到△ACO为等腰直角三角形,AC=2,然后分类讨论:当AE=AC=2时,以A点为圆心,2画弧交x轴于E1点和E2点,再写出它们的坐标;当CE=CA时,E3点与点A关于y轴对称,即可得到它的坐标;当EA=EC时,E4点为坐标原点.
解:(1)把A(-2,0)代入y=2x+m得-4+m=0,解得m=4,
∴y=-2x+4,
∵AB=4,A(-2,0),
∴B点坐标为(2,0),
把B(2,0)代入y=-x+n得-2+n=0,解得n=2,
∴y=-x+2,
解方程组,得,
∴D点坐标为(, );
(2)当x=0时,y=-x+2=2,
∴C点坐标为(0,2),
∴四边形AOCD的面积=S△DAB-S△COB
=×4×-×2×2=;
(3)如图所示,
∵A(-2,0),C(0,2),
∴AC=2,
当AE=AC=2时,E1点的坐标为(2-2,0),E2点的坐标为(-2-2,0);
当CE=CA时,E3点的坐标为(2,0),
当EA=EC时,E4点的坐标为(0,0),
综上所述,点E的坐标为(2-2,0)、(-2-2,0)、(2,0)、(0,0).
“点睛”本题考查了两条直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了分类讨论思想的运用.
26.(1)k=3,m=-1;(2)①PM=PN;②-1≤b﹤0或b≤-3.
【解析】试题分析:(1)将A点代入y=x+2中即可求出m的值,然后将A的坐标代入反比例函数中即可求出k的值.
(2)①当a=-1时,分别求出M、N两点的坐标即可求出PM与PN的关系;
②由题意可知:P的坐标为(b,b)(b<0),由于PN≥PM,从而可知PN≥2,根据图象可求出b的范围.
解:(1)∵函数的图象与直线交于点A(-3,m),
∴m=-3+2=-1,
∴A(-3,-1). k=-1×(-3)=3
即k的值是3,m的值是-1
(2)①当a =-1时,又点P(a,b)是直线y=x-2上,
∴P(-1,-1)
令y=-1,代入,得:x=-3,
∴M(-3,-1),
PM=2
令x=-1,代入,得y=-3,
∴N(-1,-3),
∴PN=2
∴PM=PN
②P(b,b),b<0
点P在直线y=x上,
过点P作平行于x轴的直线,交直线y=x+2于点M,
M(b+2,b),
∴PM=2,
∵PN≥PM,
即PN≥2,
∵PN=| |,
∴| |≥2
∴-1≤b﹤0或b≤-3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
第17章函数及其图像单元检测提高卷
班级__________姓名____________总分___________
一、选择题
1.在平面直角坐标系中,点P(m+1,2﹣m)在第二象限,则m的取值范围为( )
A. m<﹣1 B. m<2 C. m>2 D. ﹣1<m<2
2.已知点在第二象限,若点到轴的距离与到轴的距离之和是6,则的值为( )
A. 1 B. C. 5 D. 3
3.函数的自变量x的取值范围为( )
A. x≠1 B. x>-1 C. x≥-1 D. x≥-1且 x≠1
4.如表列出了一项实验的统计数据:
它表示皮球从一定高度落下时,下落高度y与弹跳高度x的关系,能表示变量y与x之间的关系式为( )
A. y=2x-10 B. y= C. y=x+25 D. y=x+5
5.已知点P(m,n)是一次函数y=x﹣1的图象位于第一象限部分上的点,其中实数m、n满足,则点P的坐标为( )
A. (,) B. (,) C. (2,1) D. (,)
6.已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
7.直线y=(3-π)x经过的象限是( )
A. 一、二象限 B. 一、三象限 C. 二、三象限 D. 二、四象限
8.根据如图的程序,计算当输入值x=﹣2时,输出结果y为( )
A. 1 B. 5 C. 7 D. 以上都有可能
9.(2017湖南怀化第8题)一次函数的图象经过点,且与轴、轴分别交于点、,则的面积是( )
A. B. C. 4 D. 8
10.如图,直线y=﹣x+m与y=nx+4n的交点的横坐标为﹣2,则关于x的不等式nx+4n>﹣x+m>0的整数解可能是( )
A. 1 B. ﹣1 C. ﹣2 D. ﹣3
二、填空题
11.如图,已知一次函数y=﹣x+3 当x________时,y=﹣2;
当x________时,y<﹣2;
当x________时,y>﹣2;
当﹣3<y<3时,x的取值范围是________.
12.如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是________.
13.如图,直线l1的解析式是y=2x-1,直线l2的解析式是y=x+1,则方程组的解是________.
14.(2015黄石,第15题,3分)一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表.现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性返还现金4元,则购买盒子所需要最少费用为________元.
15.如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为1的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在直线l上,则点A2015的坐标是______________.
16.如图,点A是反比例函数(x>0)图象上一点,过点A作x轴的平行线,交反比例函数(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为______.
三、解答题
17.周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
18.如图,已知一次函数y=x+b的图象与反比例函数(x<0)的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当时,请直接写出x的取值范围.
19.已知点A(a,0)、B(b,0),且 +|b﹣2|=0.
(1)求a、b的值.
(2)在y轴的正半轴上找一点C,使得三角形ABC的面积是15,求出点C的坐标.
(3)过(2)中的点C作直线MN∥x轴,在直线MN上是否存在点D,使得三角形ACD的面积是三角形ABC面积的?若存在,求出点D的坐标;若不存在,请说明理由.
20.已知一次函数 EMBED Equation.DSMT4 的图象与x轴、y轴分别相交于点A、B,点P在该函数的图象上,P到x轴、y轴的距离分别为、.
(1)当P为线段AB的中点时,求的值;
(2)直接写出的范围,并求当时点P的坐标;
(3)若在线段AB上存在无数个P点,使(a为常数),求a的值.
21.如图,已知A( 4,2)、B(a, 4)是一次函数y=kx+b的图象与反比例函数 EMBED Equation.DSMT4 的图象的两个交点;
(1)求此反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
22.如图,直线l是一次函数y=kx+b的图象,点A、B在直线l上.根据图象回答下列问题:
(1)写出方程kx+b=0的解;
(2)写出不等式kx+b>1的解集;
(3)若直线l上的点P(m,n)在线段AB上移动,则m、n应如何取值.
23.(2017湖南省长沙市,第24题,9分)自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该欧洲客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件.已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出.设购进A型商品m件,求该客商销售这批商品的利润v与m之间的函数关系式,并写出m的取值范围;
(3)在(2)的条件下,欧洲客商决定在试销活动中每售出一件A型商品,就从一件A型商品的利润中捐献慈善资金a元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.
24.如图,P1、P2是反比例函数(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(1)求反比例函数的解析式.
(2)①求P2的坐标.
②根据图象直接写出在第一象限内当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数的函数值.
25.如图,直线y=2x+m(m>0) 与x轴交于点A(-2,0) (, ),直线与轴、轴分别交于、两点,并与直线相交于点,若.
(1)求点的坐标;
(2)求出四边形的面积;
(3)若为轴上一点,且为等腰三角形,直接写出点的坐标.
26.如图,在平面直角坐标系xoy中,函数(x<0)的图象与直线y=x+2交于点A(-3,m).
(1)求k,m的值;
(2)已知点P(a,b)是直线y=x上,位于第三象限的点,过点P作平行于x轴的直线,交直线y=x+2于点M,过点P作平行于y轴的直线,交函数(x<0)的图象于点N.
①当a=-1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM结合函数的图象,直接写出b的取值范围.
参考答案
1.A
【解析】根据题意,得:,解得m<﹣1,
故选A.
2.B
【解析】根据题意,先由点P(2a,1-3a)在第二象限,可知2a<0,1-3a>0,求得a<0,a<,可得a的取值范围:a<0,然后由点P到x轴的距离与到y轴的距离之和为6,可得|2a|+|1-3a|=6,即-2a+1-3a=6,解得a=-1,
故选:B.
点睛:本题考查的知识点为:第二象限点的符号为(-,+);负数的绝对值为它的相反数;正数的绝对值为它本身.
3.A
【解析】试题解析:根据题意得: x-1≠0,
解得: x≠1.
故选A.
4.A
【解析】根据题意,设函数关系式为y=kx+b,
则
解得: ,
则y=2x-10.
故选:A.
5.D
【解析】解:∵,化简,得(m+n)2=4,∵点P(m,n)是一次函数y=x﹣1的图象位于第一象限部分上的点,∴n=m﹣1,∴,解得:或.
∵点P(m,n)是一次函数y=x﹣1的图象位于第一象限部分上的点,∴m>0,n>0,故点P的坐标为(1.5,0.5),故选D.
6.A
【解析】试题解析:∵k+b=﹣5,kb=6,∴k<0,b<0识.
∴根据一次函数图象与系数的关系:
①当k>0,b>0时,函数y=kx+b的图象经过第一、二、三象限;
②当k>0,b<0时,函数y=kx+b的图象经过第一、三、四象限;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限.
∴直线y=kx+b经过二、三、四象限,不经过第一象限.
故选A.
7.D
【解析】由题意得: ,则直线经过. 二、四象限.故选D.
8.C
【解析】先由x=﹣2≤﹣1,确定x与y的关系式为y=x2+3,然后代值计算即可.
解:∵x=﹣2≤﹣1,
∴y=x2+3=(﹣2)2+3=7,
故选C.
9.B
【解析】试题解析:∵一次函数y=﹣2x+m的图象经过点P(﹣2,3),
∴3=4+m,
解得m=﹣1,
∴y=﹣2x﹣1,
∵当x=0时,y=﹣1,
∴与y轴交点B(0,﹣1),
∵当y=0时,x=﹣,
∴与x轴交点A(﹣,0),
∴△AOB的面积:V×1×=.
故选B.
10.B
【解析】∵直线y= x+m与y=nx+4n的交点的横坐标为 2,
∴关于x的不等式nx+4n>﹣x+m>0的解集为 2< x<0,
∴整数解可能是 1.
故选:B.
11. =5 >5 <5 0<x<6
【解析】如图,
当x=5时,y= 2;
当x>5时,y< 2;
当x<5时,y> 2;
当0
12.x>-2
【解析】试题解析:从图象得到,当x>-2时,y=3x+b的图象对应的点在函数y=ax-3的图象上面,
∴不等式3x+b>ax-3的解集为:x>-2.
13.
【解析】试题分析:以二元一次方程组的两个方程画出的两个一次函数图像的交点就是二元一次方程组的解,本题中的交点坐标为(2,3),则方程组的解为: .
14.29.
【解析】解:设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为个。
①当0≤x<3时,=,∵k=1>0,∴y随x的增大而增大,∴当x=0时,y有最小值,最小值为30元;
②当时,=,∵k=1>0,∴y随x的增大而增大,∴当x=3时,y有最小值,最小值为29元;
综合①②可得,购买盒子所需要最少费用为29元.故答案为:29.
15.(,).
【解析】解:过B1向x轴作垂线B1C,垂足为C,由题意可得:A(1,0),AO∥A1B1,∠B1OC=30°,∴CB1=OB1cos30°=,∴B1的横坐标为:,则B1的纵坐标为:,∴点B1,B2,B3,…都在直线上,∴B1(,),等边三角形的边长为1可得出:A的横坐标为:1,∴y=,∴A2(2,),…
An(,).∴A2015(,).故答案为:(,).
16.5.
【解析】解:延长BA,与y轴交于点C.∵AB∥x轴,∴BC⊥y轴.∵A是反比例函数(x>0)图象上一点,B为反比例函数(x>0)的图象上的点,∴S△AOC=,S△BOC=.∵S△AOB=2,即=2,解得:k=5.故答案为:5.
17.(1)0.5 h.(2)1.75h,25km
【解析】试题分析:(1)用路程除以时间即可得到速度;在甲地游玩的时间是1-0.5=0.5小时;
(2)先求出妈妈驾车的速度,设妈妈从出发到追上小明的时间为t小时,根据妈妈追上小明时两人所走过的路程相等,列方程进行求解即可得.
试题解析:(1)小明骑车速度: =20(km/h),在甲地游玩的时间是1-0.5=0.5 h.
(2)妈妈驾车速度:20×3=60(km/h),
设妈妈从出发到追上小明的时间为t(h),由题意得20(t+)=60t,解得t= ,
所以小明出发+=1.75(h)后被妈妈追上,此时离家×60=25(km).
18.(1)C(0,);(2)x<﹣4或﹣1<x<0.
【解析】试题分析:(1)作点A关于y轴的对称点A′,连接A′B交y轴于点C,此时点C即是所求.由点A为一次函数与反比例函数的交点,利用待定系数法和反比例函数图象点的坐标特征即可求出一次函数与反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点A、B的坐标,再根据点A′与点A关于y轴对称,求出点A′的坐标,设出直线A′B的解析式为y=mx+n,结合点的坐标利用待定系数法即可求出直线A′B的解析式,令直线A′B解析式中x为0,求出y的值,即可得出结论;
(2)根据两函数图象的上下关系结合点A、B的坐标,即可得出不等式的解集.
试题解析:解:(1)作点A关于y轴的对称点A′,连接A′B交y轴于点C,此时点C即是所求,如图所示.
∵反比例函数(x<0)的图象过点A(﹣1,2),∴k=﹣1×2=﹣2,∴反比例函数解析式为(x<0);
∵一次函数y=x+b的图象过点A(﹣1,2),∴2=﹣+b,解得:b=,∴一次函数解析式为.联立一次函数解析式与反比例函数解析式成方程组:,解得:,或,∴点A的坐标为(﹣1,2)、点B的坐标为(﹣4,).
∵点A′与点A关于y轴对称,∴点A′的坐标为(1,2),设直线A′B的解析式为y=mx+n,则有,解得:,∴直线A′B的解析式为.令中x=0,则y=,∴点C的坐标为(0,).
(2)观察函数图象,发现:当x<﹣4或﹣1<x<0时,一次函数图象在反比例函数图象下方,∴当时,x的取值范围为x<﹣4或﹣1<x<0.
19.(1)a=﹣4,b=2;(2)C(0,5);(3)D(3,5)或(﹣3,5).
【解析】试题分析:(1)根据非负数的性质列方程,解方程即可得到结论;
(2)由A(﹣4,0)、B(2,0),得到AB=6,根据三角形ABC的面积是15,列方程求解即可得到结论;
(3)根据三角形ABC的面积是15列方程,解方程即可得到结论.
试题解析:解:(1)∵(a+4)2+|b﹣2|=0,∴a+4=0,b﹣2=0,∴a=﹣4,b=2;
(2)如图1,∵A(﹣4,0)、B(2,0),∴AB=6,∵三角形ABC的面积是15,∴ AB OC=15,∴OC=5,∴C(0,5);
(3)存在,如图2,∵三角形ABC的面积是15,∴S△ACD=CD OC=×15,∴CD×5=×15,∴CD=3,∴D(3,5)或(﹣3,5).
点睛:本题考查了坐标与图形的性质,非负数的性质,三角形的面积,正确作出图形是解题的关键.
20.(1)3;(2), P的坐标为(1,2)或(, );(3)2.
【解析】试题分析:(1)对于一次函数解析式,求出A与B的坐标,即可求出P为线段AB的中点时的值;
(2)根据题意确定出的范围,设P(m,2m﹣4),表示出,分类讨论m的范围,根据求出m的值,即可确定出P的坐标;
(3)设P(m,2m﹣4),表示出与,由P在线段上求出m的范围,利用绝对值的代数意义表示出与,代入,根据存在无数个点P求出a的值即可.
试题解析:解:(1)对于一次函数,令x=0,得到y=﹣4;令y=0,得到x=2,∴A(2,0),B(0,﹣4),∵P为AB的中点,∴P(1,﹣2),则;
(2)①;
②设P(m,2m﹣4),∴=,当0≤m≤2时, =m+4﹣2m=4﹣m=3,解得:m=1,此时P1(1,﹣2);
当m>2时, =m+2m﹣4=3,解得:m=,此时P2(, );
当m<0时,不存在,综上,P的坐标为(1,﹣2)或(, );
(3)设P(m,2m﹣4),∴=, =,∵P在线段AB上,∴0≤m≤2,∴=4﹣2m, =m,∵,∴4﹣2m+am=4,即(a﹣2)m=0,∵有无数个点,∴a=2.
21.(1)反比例函数的解析式为,一次函数的解析式为y=-x-2(2)-4
【解析】试题分析:(1)把A点坐标代入反比例函数解析式求出m的值,再把B点坐标代入反比例函数解析式求出a的值,从而得出点B的坐标,根据点A、B的坐标利用待定系数法即可求出直线AB的解析式;
(2)由两函数图象的上下位置关系结合交点的横坐标,即可得出使一次函数值小于反比例函数值的x的取值范围.
试题解析:
解:(1)∵m=xy=(-4)×2=-8,
∴反比例函数的解析式为y=.
∴-4a=-8,
∴a=2,
y=kx+b过A(-4,2),B(2,-4)两点,
∴,
解得.
故一次函数的解析式为y=-x-2;
(2)观察函数图象可知:当-4<x<0或x>2时,一次函数图象在反比例函数图象下方,
∴一次函数的值小于反比例函数值的x的取值范围:-4<x<0或x>2.
点睛:本题考查了待定系数法求反比例函数和一次函数解析式、反比例函数与一次函数图象上点的坐标特征,解题的关键是:(1)根据点的坐标利用待定系数法求反比例函数和一次函数解析式;(2)根据两函数图象的上下位置关系找出使一次函数的值小于反比例函数的值的x的取值范围.
22.(1)x=-2;(2)x>0;(3)0≤n≤2
【解析】试题分析:从图象上得到函数的增减性及与坐标轴的交点的坐标后,解答各题.
试题解析:(1)函数经过点(-2,0),则方程的根是
答:
(2)函数经过点(0,1),则当时,有
即不等式的解集是
答
(3)线段的自变量的取值范围是:
当时,函数值的范围是
则.
答:
23.(1)一件B型商品的进价为150元,一件A型商品的进价为160元;(2)v=10m+17500(80≤m≤125);(3)当a<10时,最大利润为(18750﹣125a)元;当a=10时,最大利润为17500元;当a>10时,最大利润为(18300﹣80a)元.
【解析】试题分析:(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+10)元.根据16000元采购A型商品的件数是用7500元采购B型商品的件数的2倍,列出方程即可解决问题;
(2)根据总利润=两种商品的利润之和,列出式子即可解决问题;
(3)设利润为w元.则w=(80﹣a)m+70(250﹣m)=(10﹣a)m+17500,分三种情形讨论即可解决问题.
试题解析:解:(1)设一件B型商品的进价为x元,则一件A型商品的进价为(x+10)元.
由题意:,解得x=150,经检验x=150是分式方程的解.
答:一件B型商品的进价为150元,一件A型商品的进价为160元.
(2)因为客商购进A型商品m件,所以客商购进B型商品(250﹣m)件.
由题意:v=80m+70(250﹣m)=10m+17500,∵80≤m≤250﹣m,∴80≤m≤125,∴v=10m+17500(80≤m≤125);
(3)设利润为w元.则w=(80﹣a)m+70(250﹣m)=(10﹣a)m+17500:
①当10﹣a>0时,w随m的增大而增大,所以m=125时,最大利润为(18750﹣125a)元.
②当10﹣a=0时,最大利润为17500元.
③当10﹣a<0时,w随m的增大而减小,所以m=80时,最大利润为(18300﹣80a)元,∴当a<10时,最大利润为(18750﹣125a)元;当a=10时,最大利润为17500元;当a>10时,最大利润为(18300﹣80a)元.
点睛:本题考查了分式方程的应用、一次函数的应用等知识,解题的关键是理解题意,学会构建方程或一次函数解决问题,属于中考常考题型.
24.(1);(2)①P2(,);②2<x<.
【解析】试题分析:(1)先根据点A1的坐标为(4,0),△P1OA1为等腰直角三角形,求得P1的坐标,再代入反比例函数求解;(2)先根据△P2A1A2为等腰直角三角形,将P2的坐标设为(4+a,a),并代入反比例函数求得a的值,得到P2的坐标;再根据P1的横坐标和P2的横坐标,判断x的取值范围.
试题解析:解:(1)过点P1作P1B⊥x轴,垂足为B.∵点A1的坐标为(4,0),△P1OA1为等腰直角三角形,∴OB=2,P1B=OA1=2,∴P1的坐标为(2,2).将P1的坐标代入反比例函数(k>0),得k=2×2=4,∴反比例函数的解析式为;
(2)①过点P2作P2C⊥x轴,垂足为C.∵△P2A1A2为等腰直角三角形,∴P2C=A1C.设P2C=A1C=a,则P2的坐标为(4+a,a),将P2的坐标代入反比例函数的解析式为,得:,解得a1=,a2=(舍去),∴P2的坐标为(,);
②在第一象限内,当2<x<时,一次函数的函数值大于反比例函数的值.
25.(1)D点坐标为(, );(2);(3)点E的坐标为(2-2,0)、(-2-2,0)、(2,0)、(0,0).
【解析】(1)先把A点坐标代入y=2x+m得到m=4,则y=-2x+4,再利用AB=4可得到B点坐标为(2,0),则把B点坐标代入y=-x+n可得到n=2,则y=-x+2,然后根据两直线相交的问题,通过解方程组得到D点坐标;
(2)先确定C点坐标为(0,2),然后利用四边形AOCD的面积=S△DAB-S△COB进行计算即可;
(3)先利用A、C两点的坐标特征得到△ACO为等腰直角三角形,AC=2,然后分类讨论:当AE=AC=2时,以A点为圆心,2画弧交x轴于E1点和E2点,再写出它们的坐标;当CE=CA时,E3点与点A关于y轴对称,即可得到它的坐标;当EA=EC时,E4点为坐标原点.
解:(1)把A(-2,0)代入y=2x+m得-4+m=0,解得m=4,
∴y=-2x+4,
∵AB=4,A(-2,0),
∴B点坐标为(2,0),
把B(2,0)代入y=-x+n得-2+n=0,解得n=2,
∴y=-x+2,
解方程组,得,
∴D点坐标为(, );
(2)当x=0时,y=-x+2=2,
∴C点坐标为(0,2),
∴四边形AOCD的面积=S△DAB-S△COB
=×4×-×2×2=;
(3)如图所示,
∵A(-2,0),C(0,2),
∴AC=2,
当AE=AC=2时,E1点的坐标为(2-2,0),E2点的坐标为(-2-2,0);
当CE=CA时,E3点的坐标为(2,0),
当EA=EC时,E4点的坐标为(0,0),
综上所述,点E的坐标为(2-2,0)、(-2-2,0)、(2,0)、(0,0).
“点睛”本题考查了两条直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了分类讨论思想的运用.
26.(1)k=3,m=-1;(2)①PM=PN;②-1≤b﹤0或b≤-3.
【解析】试题分析:(1)将A点代入y=x+2中即可求出m的值,然后将A的坐标代入反比例函数中即可求出k的值.
(2)①当a=-1时,分别求出M、N两点的坐标即可求出PM与PN的关系;
②由题意可知:P的坐标为(b,b)(b<0),由于PN≥PM,从而可知PN≥2,根据图象可求出b的范围.
解:(1)∵函数的图象与直线交于点A(-3,m),
∴m=-3+2=-1,
∴A(-3,-1). k=-1×(-3)=3
即k的值是3,m的值是-1
(2)①当a =-1时,又点P(a,b)是直线y=x-2上,
∴P(-1,-1)
令y=-1,代入,得:x=-3,
∴M(-3,-1),
PM=2
令x=-1,代入,得y=-3,
∴N(-1,-3),
∴PN=2
∴PM=PN
②P(b,b),b<0
点P在直线y=x上,
过点P作平行于x轴的直线,交直线y=x+2于点M,
M(b+2,b),
∴PM=2,
∵PN≥PM,
即PN≥2,
∵PN=| |,
∴| |≥2
∴-1≤b﹤0或b≤-3
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
