7.1 不等式及其基本性质同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
7.1 不等式及其基本性质同步练习
　班级__________姓名____________总分___________
本节应掌握和应用的知识点
１.用不等号表示不等关系的式子叫做不等式,其中不等号包括＞,≥,＜,≤或≠．
２.不等式的基本性质:
(１)如果a＞b,那么a±c ＞b±c;
(２)如果a＞b,c＞０,那么ac ＞ bc,＞;
(３)如果a＞b,c＜０,那么ac ＜ bc,＜
(４)如果a＞b,那么b＜a;
(５)如果a＞b,b＞c,那么a＞c．
基础知识和能力拓展精练
一、选择题
1．（2016黑龙江省大庆市）当0＜x＜1时，、x、的大小顺序是（　　）
A. B. C. D.
2．若a＞b，则下列不等式变形错误的是(　　)
A. a＋2＞b＋2 B. － EMBED Equation.DSMT4 ＜－ C. 3－a＞3－b D. 4a－1＞4b－1
3．下列式子中，是不等式的有(　　)．
①2x＝7；②3x＋4y；③－3＜2；④2a－3≥0；⑤x＞1；⑥a－b＞1.
A. 5个 B. 4个 C. 3个 D. 1个
4．下列按条件列出的不等式中，正确的是( )
A. a不是负数，则a＞0 B. a与3的差不等于1，则a－3＜1
C. a是不小于0的数，则a＞0 D. a与 b的和是非负数，则a＋b≥0
5．（2017江苏省常州市）若3x＞﹣3y，则下列不等式中一定成立的是（　 ）
A. x+y＞0 B. x﹣y＞0 C. x+y＜0 D. x﹣y＜0
6．如图，下列结论正确的是（　　）
A. B. C. D.
7．据中央气象台报道，某日上海最高气温是22 ℃，最低气温是11 ℃，则当天上海气温t(℃)的变化范围是( )
A. t＞22 B. t≤22 C. 11＜t＜22 D. 11≤t≤22
8．已知x＞y，若对任意实数a，以下结论：甲：ax＞ay；乙：a2－x＞a2－y；丙：a2＋x≤a2＋y；丁：a2x≥a2y，其中正确的是( )
A. 甲 B. 乙 C. 丙 D. 丁
二、填空题
9．如图，身高为xcm的1号同学与身高为ycm的2号同学站在一起时，如果用一个不等式来表示他们的身高关系，则这个式子可以表示成x__y（用“＞”或“＜”填空）．
1号 2号
10．按商品质量规定：商店出售的标明500 g的袋装食盐，其实际克数与所标克数相差不能超过5 g．设实际克数为x(g)，则x应满足的不等式是_____．
11．当m________时，不等式mx＜7的解集为x＞
12．若a＜b，c＜0，则2a________2b，a+c________b+c， ________（用不等号填空）
13．已知关于x的不等式(m－1)x＞6，两边同除以m－1，得x＜，则化简：|m－1|－|2－m|＝______．
三、解答题
14．甲地离学校4 km，乙地离学校1 km，记甲、乙两地之间的距离为d(km)，求d的取值范围．
15．利用不等式的基本性质，将下列不等式化为“x>a”或“x(1)x＋2>7.
(2)3x<－12.
(3)－7x>－14.
(4) x<2.
16．现有不等式的两个性质：①在不等式的两边都加上(或减去)同一个数(或整式)，不等号的方向不变．②在不等式的两边都乘同一个数(或整式)，乘的数(或整式)为正时不等号的方向不变，乘的数(或整式)为负时不等号的方向改变．
请解决以下两个问题：
(1)利用性质①比较2a 与a 的大小(a≠0)．
(2)利用性质②比较2a 与a 的大小(a≠0)．
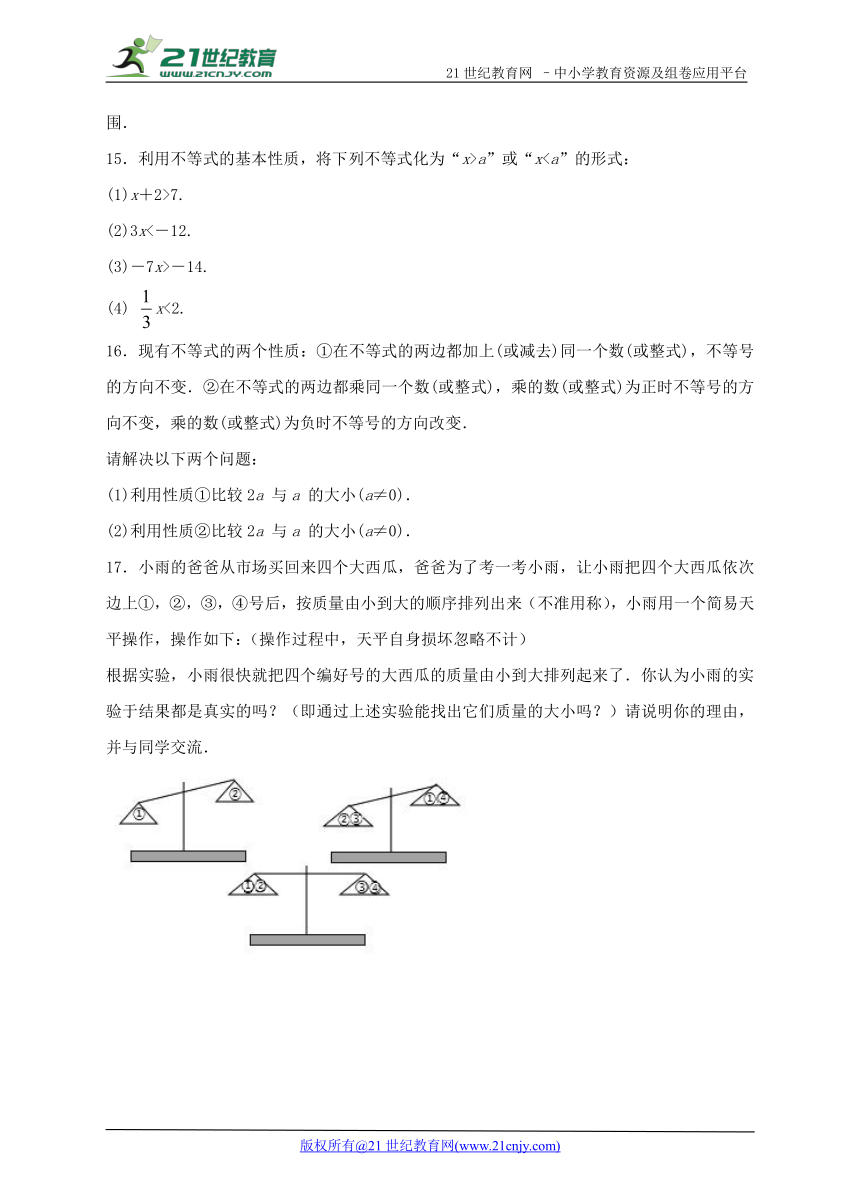
17．小雨的爸爸从市场买回来四个大西瓜，爸爸为了考一考小雨，让小雨把四个大西瓜依次边上①，②，③，④号后，按质量由小到大的顺序排列出来（不准用称），小雨用一个简易天平操作，操作如下：（操作过程中，天平自身损坏忽略不计）
根据实验，小雨很快就把四个编好号的大西瓜的质量由小到大排列起来了．你认为小雨的实验于结果都是真实的吗？（即通过上述实验能找出它们质量的大小吗？）请说明你的理由，并与同学交流．
参考答案
1．A
【解析】当0＜x＜1时，在不等式0＜x＜1的两边都乘上x，可得0＜＜x，在不等式0＜x＜1的两边都除以x，可得0＜1＜，
又∵x＜1，∴、x、的大小顺序是：，
故选A．
2．C
【解析】A.根据不等式的性质1，在a>b的两边都加2，不等号方向不改变，故正确；
B.根据不等式的性质3，在a>b的两边都乘 ，不等号方向改变，故正确；
C.根据不等式的性质3，在a>b的两边都乘 ，得－a<－b，根据不等式的性质1，在－a<－b 的两边都加3，不等号方向不改变，故错误；
D.先根据不等式的性质3，在a>b的两边都乘4，不等号方向不改变，得4a>4b，再根据性质1得4a－1＞4b－1，故正确；
故选：C.
3．B
【解析】解：不等式有：③－3＜2；④2a－3≥0；⑤x＞1；⑥a－b＞1，共4个．故选B．
4．D
【解析】根据a不是负数，则a可能是正数和0，即a≥0，故不正确；
根据a与3的差不等于1，可知a-3≠1，故不正确；
根据a是不小于0的数，即可知a≥0，故不正确；
根据非负数的意义，可知a+b≥0，故正确.
故选：D
5．A
【解析】两边都除以3，得x＞﹣y，两边都加y，得：x+y＞0，
故选A．
6．B
【解析】选项A. ,错误.
选项B. ,正确.
选项C. ,错误.
选项D. ,错误.
故选B.
7．D
【解析】气温最高是22℃，则t≤22；
气温最低是11℃，则t≥11.
故气温的变化范围11≤t≤22.
故选D.
8．D
【解析】甲：当a=0时，ax=ay，故甲错误；
乙：由x＞y，所以-x<-y，所以a2－x丙：由x＞y，所以a2＋x>a2＋y，故丙错误；
丁：当a=0时，a2x=a2y，当a≠0时，a2x>a2y，所以a2x≥a2y，故丁正确.
故选D.
点睛：熟记不等式的性质：①如果a>b，那么a+c>b+c，a-c>b-c；②如果a>b，并且c>0，那么ac>bc， ；③如果a>b，并且c<0，那么ac9．＜
【解析】如果用一个不等式来表示他们的身高关系，则这个式子可以表示成x＜y，
故答案为：＜．
10．495≤x≤505
【解析】根据题意，可知x应满足的不等式是500-5≤x≤500+5，即495≤x≤505.
故答案为：495≤x≤505.
11．＜0
【解析】试题解析：∵不等式mx＜7的解集为x＞，
∴m＜0．
故答案为：＜0．
12． ＜ ＜ ＞
【解析】根据不等式的性质，由a＜b，2＞0，c＜0，可得2a＜2b，a+c＜b+c， ，
故答案为：＜，＜，＞.
13．-1
【解析】因为（m-1）x＞6，两边同除以m-1，得x＜，
所以m-1＜0，m＜1，
所以2-m＞0，
所以|m-1|-|2-m|
=（1-m）-（2-m）
=1-m-2+m
=-1
故答案是：-1.
【点睛】此题主要考查了不等式的基本性质：（1）不等式的两边同时乘以（或除以）同一个正数，不等号的方向不变；（2）不等式的两边同时乘以（或除以）同一个负数，不等号的方向改变；（3）等式的两边同时加上（或减去）同一个数或同一个含有字母的式子，不等号的方向不变；解答此题的关键是判断出m-1＜0．
14．甲、乙之间的距离在3～5 km之间
【解析】试题分析：甲乙都在学校同侧，且甲乙与学校在同一直线上时，甲乙两地的距离最小；甲乙在学校两侧，且甲乙与学校在同一直线上时，甲乙两地的距离最大；当甲乙以及学校不在同一直线上时，甲乙的距离在前面两个距离之间．
试题解析：①当甲、乙、学校三者在同一直线上时，
若甲、乙在学校的两侧，则甲、乙相距最远为5 km；
若甲、乙在学校的同侧，则甲、乙相距最近为3 km.
②当甲、乙、学校三者不在同一直线上时，
甲、乙之间的距离在3～5 km之间．
点睛：本题考查的是三角形的三边关系，先分别求出三点同线的情况，即最短距离和最长距离两种情况，则d的取值即在这两者之间．
15．（1）x>5;(2)x<-4;(3)x<2;(4)x<6
【解析】试题分析：（1）不等式两边都减去2即可；
（2）两边都除以3即可；
（3）两边都除以－7，改变不等号方向即可；
（4）两边都乘3即可.
试题解析：
（1）两边都减去2，得x>5
（2）两边都除以3，得x<－4.
（3）两边都除以－7，得x<2.
（4）两边都乘3，得x<6.
16．(1)2a【解析】试题分析：（1）根据不等式的性质①，可得答案；
（2）根据不等式的性质②，可得答案．
试题解析：
(1)当a＞0时，a＋a＞a＋0，即2a＞a.
当a＜0时，a＋a＜a＋0，即2a＜a.
(2)当a＞0时，由2＞1，得2·a＞1·a，即2a＞a.
当a＜0时，由2＞1，得2·a＜1·a，即2a＜a.
17．③＞①＞②＞④
【解析】试题分析：利用已知天平得出：①＞②，②+③＞①+④，①+②=③+④，进而比较得出即可．
试题解析：由题意可得：①＞②，②+③＞①+④，①+②=③+④，
因为 ①＞②，②+③＞①+④，所以②+③＞①+④＞②+④，所以③＞④；
因为①+②=③+④，所以①﹣③=④﹣②，又②+③＞①+④，
所以②﹣④＞①﹣③＞④﹣②，所以②＞④，所以①＞②＞④；
因为①+②=③+④，所以①﹣④=③﹣②＞0，
所以③＞②；④﹣②＜0，所以①﹣③＜0，所以③＞①；
综上，③＞①＞②＞④．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)