人教版数学四年级下课件:5 三角形的内角和
文档属性
| 名称 | 人教版数学四年级下课件:5 三角形的内角和 |  | |
| 格式 | pptx | ||
| 文件大小 | 393.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-03 21:39:58 | ||
图片预览








文档简介
(共24张PPT)
第5单元 三角形
第3节 三角形的内角和
第1课时 三角形的内角和
课前谈话
复习引入
回顾
我们以前学过哪些平面图形?
说一说
你能说说长方形的特征吗?
对边相等,有4个角,4个角都是直角。
这4个角一共是多少度呢?
360°
4个直角可以拼成2个平角。
360°相当于几个平角?
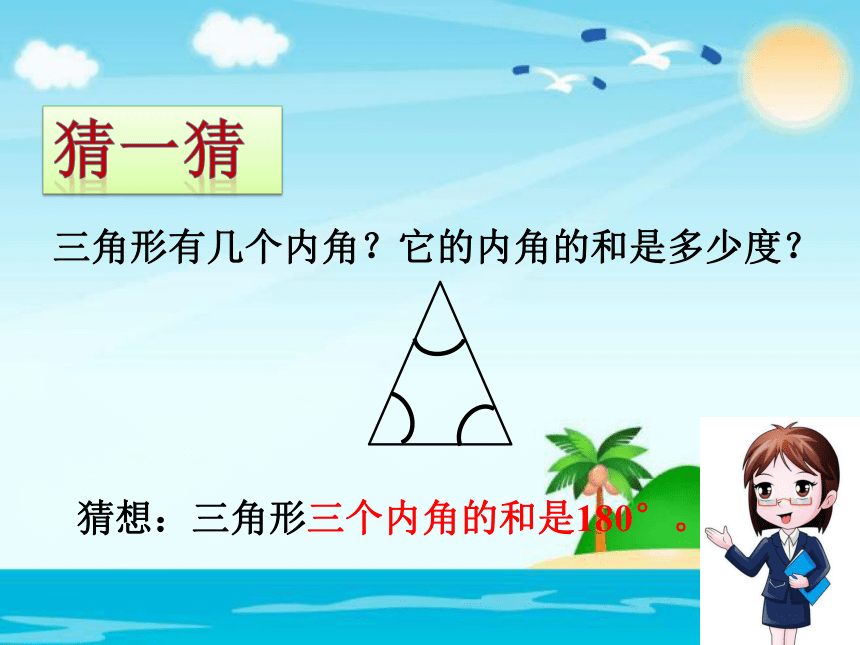
三角形有几个内角?它的内角的和是多少度?
猜想:三角形三个内角的和是180°。
猜一猜
探究新知
小组合作
同学们能够用什么样的方法来证明三角形的内角和是180°呢?
要求:
小组合作,利用学具进行验证。
汇报交流
方法一:量角器测量
① 测量出三个内角的度数,求出和是180°;
②先假设是180°,测量出角1和角2的度数,算出第三个角的度数,再用量角器测量验证第三个角是否是算出的结果。
汇报交流
方法二:剪拼
直角三角形、钝角三角形呢?
汇报交流
方法三:折
将三角形的三个角折成一个平角。
方法四:推理
根据“长方形的内角和是360°”推理出三角形的内角和是180°。
小结
刚才同学们用量、折、剪、拼、计算、推理等这么多巧妙的方法得出,无论是什么样的三角形的内角和都是180°。
解决问题
做一做
1.在右图中,∠1= 140°,
∠3= 25°。求∠2的度数。
解:∠2= 180°-∠1 -∠3
=180°-140°-25°
=15°
做一做
2.把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
每个小三角形的内角和是180°。
判断
1.等腰三角形一定是锐角三角形。 ( )
2.等腰直角三角形的底角一定是45度。 ( )
3.三角形越大,它的内角和就越大。 ( )
4.一个三角形至少有一个角是锐角。 ( )
√
×
×
√
填空
1.每个三角形的内角和都是( )度。
2.在三角形ABC中, ∠ A=90°,∠ B+ ∠ C= ( )。
3.在三角形中至少应该有( )个锐角。
4.在三角形ABC中, ∠ A= 25°,∠ C= 26°, ∠ B=( ),是一个( )三角形。
180
90°
2
129°
钝
填空
5.一个顶角是50°的等腰三角形的底角是( )。
6.等边三角形的每个角都是( )。
65°
60°
思考
将三角形剪下一个角也是一个小三角形,剪下的小三角形的内角和是多少度?
剩下的图形的内角和是多少度?
还原成一个大三角形后,内角和又是多少度?
180°
360°
180°
课堂小结
这节课你有什么收获。
任意三角形的内角和都是180°。
谢谢大家!
第5单元 三角形
第3节 三角形的内角和
第1课时 三角形的内角和
课前谈话
复习引入
回顾
我们以前学过哪些平面图形?
说一说
你能说说长方形的特征吗?
对边相等,有4个角,4个角都是直角。
这4个角一共是多少度呢?
360°
4个直角可以拼成2个平角。
360°相当于几个平角?
三角形有几个内角?它的内角的和是多少度?
猜想:三角形三个内角的和是180°。
猜一猜
探究新知
小组合作
同学们能够用什么样的方法来证明三角形的内角和是180°呢?
要求:
小组合作,利用学具进行验证。
汇报交流
方法一:量角器测量
① 测量出三个内角的度数,求出和是180°;
②先假设是180°,测量出角1和角2的度数,算出第三个角的度数,再用量角器测量验证第三个角是否是算出的结果。
汇报交流
方法二:剪拼
直角三角形、钝角三角形呢?
汇报交流
方法三:折
将三角形的三个角折成一个平角。
方法四:推理
根据“长方形的内角和是360°”推理出三角形的内角和是180°。
小结
刚才同学们用量、折、剪、拼、计算、推理等这么多巧妙的方法得出,无论是什么样的三角形的内角和都是180°。
解决问题
做一做
1.在右图中,∠1= 140°,
∠3= 25°。求∠2的度数。
解:∠2= 180°-∠1 -∠3
=180°-140°-25°
=15°
做一做
2.把下面这个三角形沿虚线剪成两个小三角形,每个小三角形的内角和是多少度?
每个小三角形的内角和是180°。
判断
1.等腰三角形一定是锐角三角形。 ( )
2.等腰直角三角形的底角一定是45度。 ( )
3.三角形越大,它的内角和就越大。 ( )
4.一个三角形至少有一个角是锐角。 ( )
√
×
×
√
填空
1.每个三角形的内角和都是( )度。
2.在三角形ABC中, ∠ A=90°,∠ B+ ∠ C= ( )。
3.在三角形中至少应该有( )个锐角。
4.在三角形ABC中, ∠ A= 25°,∠ C= 26°, ∠ B=( ),是一个( )三角形。
180
90°
2
129°
钝
填空
5.一个顶角是50°的等腰三角形的底角是( )。
6.等边三角形的每个角都是( )。
65°
60°
思考
将三角形剪下一个角也是一个小三角形,剪下的小三角形的内角和是多少度?
剩下的图形的内角和是多少度?
还原成一个大三角形后,内角和又是多少度?
180°
360°
180°
课堂小结
这节课你有什么收获。
任意三角形的内角和都是180°。
谢谢大家!
