人教版八年级下册数学课件:18.2.3 正方形
文档属性
| 名称 | 人教版八年级下册数学课件:18.2.3 正方形 |

|
|
| 格式 | zip | ||
| 文件大小 | 533.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-05 00:00:00 | ||
图片预览




文档简介
课件16张PPT。18.2 特殊的平行四边形第18章 平行四边形18.2.3 正方形引入你能用纸裁剪出一个正方形吗? 如图,△ABC是等腰直角三角形,BD是中线,请你画出△ABC关于点D的中心对称图形.这个四边形是什么图形?
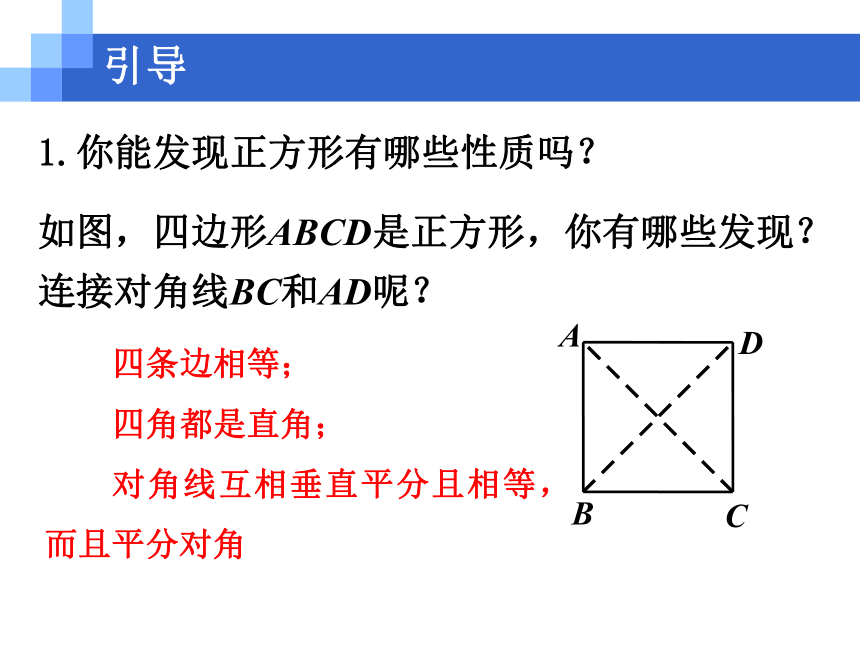
1.你能发现正方形有哪些性质吗?如图,四边形ABCD是正方形,你有哪些发现?
连接对角线BC和AD呢?引导 四条边相等;
四角都是直角;
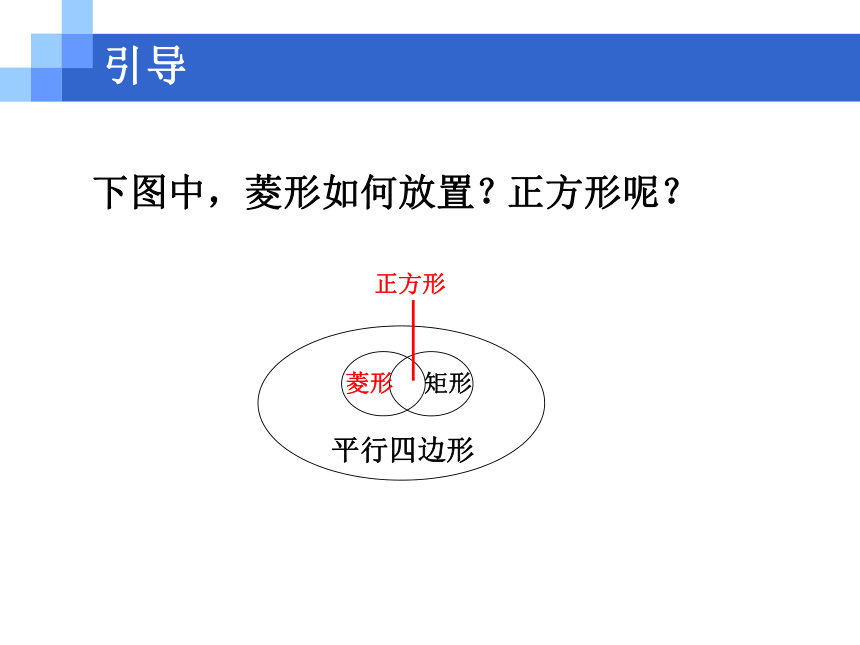
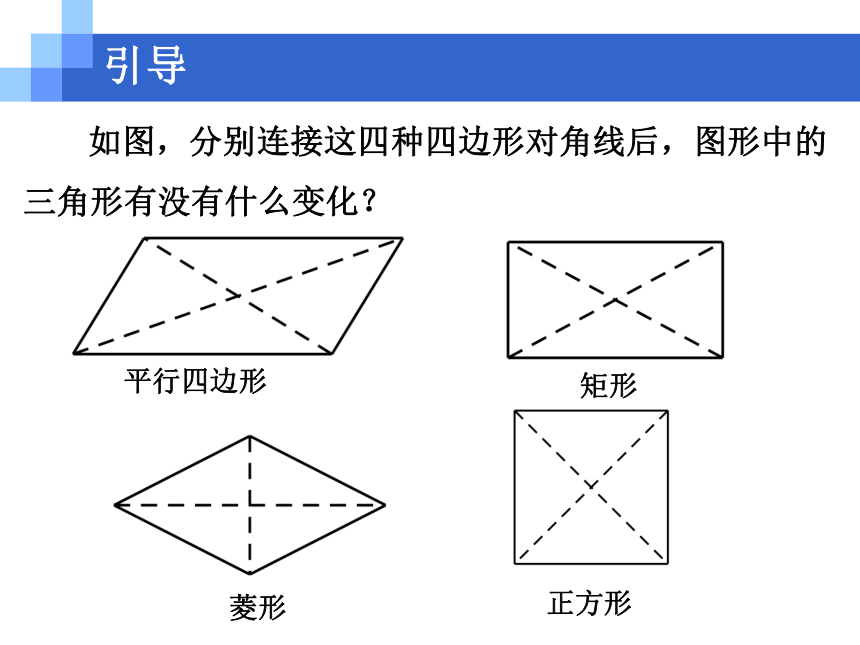
对角线互相垂直平分且相等,而且平分对角2.与其他四边形的关系. 与已经学过的特殊四边形的性质比较,你有没有一些大胆的猜测呢?并且说明你猜测的正确性. 由边(对边相等)、角(对角相等)、对角线(互相平分)都可以看出正方形是特殊的平行四边形; 由角(四个角都是直角)、对角线(相等且互相平分)都可以看出正方形是特殊的矩形; 由边(四条边相等)、对角线(互相垂直平分)都可以看出正方形是特殊的菱形.引导正方形 下图中,菱形如何放置? 正方形呢?引导平行四边形 如图,分别连接这四种四边形对角线后,图形中的三角形有没有什么变化?引导矩形菱形正方形平行四边形引导矩形菱形正方形4个三角形4个等腰三角形,其中两两全等4个全等的直角三角形4个等腰直角三角形 正方形、菱形、矩形、平行四边形之间有什么关系?列表或用框图表示这些关系.引导 例5 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ABO,△BCO,△CDO,
△DAO是全等的等腰直角三角形.证明:∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO,△BCO,△CDO,△DAO都是等腰直角三角形,并且△ABO≌△BCO≌△CDO≌△DAO.引导3.如何判定正方形?满足什么条件的矩形是正方形?你有哪些方法?类似的,如何通过菱形和平行四边形来判定正方形?引导 例6 如图所示,在△ABC中,∠ACB=90o ,CD平分∠ACB, DE⊥BC,DF⊥AC ,垂足分别为E,F .求证:四边形CFDE是正方形. 分析:要证明四边形CFDE是正方形,可先证CFDE是矩形,然后再证有一组邻边相等;也可以先证四边形CFDE是菱形,然后再证有一个角是直角. 引导引导证明:∵ CD平分∠ACB,DE⊥BC,DF⊥AC,∴ DE=DF.∵ ∠DEC=∠ECF=∠CFD=90°,∴ 四边形CFDE是矩形.∵ DE=DF,∴ 四边形CFDE是正方形. 例6 如图所示,在△ABC中,∠ACB=90o ,CD平分∠ACB, DE⊥BC,DF⊥AC ,垂足分别为E,F .求证:四边形CFDE是正方形.交流讨论: 从一张彩纸上剪出一个正方形,你能检验剪出的图形符合要求吗?你是如何检验的,与同伴交流一下.引导回顾正方形的性质和判定方法.小结 写一篇关于对正方形及我们已经学习过的其他特殊四边形认识的小论文. (友情提示:可以从体现它们一般与特殊关系的性质入手,也可以专门从判定正方形的方法入手)作业谢谢 !
1.你能发现正方形有哪些性质吗?如图,四边形ABCD是正方形,你有哪些发现?
连接对角线BC和AD呢?引导 四条边相等;
四角都是直角;
对角线互相垂直平分且相等,而且平分对角2.与其他四边形的关系. 与已经学过的特殊四边形的性质比较,你有没有一些大胆的猜测呢?并且说明你猜测的正确性. 由边(对边相等)、角(对角相等)、对角线(互相平分)都可以看出正方形是特殊的平行四边形; 由角(四个角都是直角)、对角线(相等且互相平分)都可以看出正方形是特殊的矩形; 由边(四条边相等)、对角线(互相垂直平分)都可以看出正方形是特殊的菱形.引导正方形 下图中,菱形如何放置? 正方形呢?引导平行四边形 如图,分别连接这四种四边形对角线后,图形中的三角形有没有什么变化?引导矩形菱形正方形平行四边形引导矩形菱形正方形4个三角形4个等腰三角形,其中两两全等4个全等的直角三角形4个等腰直角三角形 正方形、菱形、矩形、平行四边形之间有什么关系?列表或用框图表示这些关系.引导 例5 求证:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.已知:如图,四边形ABCD是正方形,对角线AC,BD相交于点O.
求证:△ABO,△BCO,△CDO,
△DAO是全等的等腰直角三角形.证明:∵四边形ABCD是正方形,
∴AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO,△BCO,△CDO,△DAO都是等腰直角三角形,并且△ABO≌△BCO≌△CDO≌△DAO.引导3.如何判定正方形?满足什么条件的矩形是正方形?你有哪些方法?类似的,如何通过菱形和平行四边形来判定正方形?引导 例6 如图所示,在△ABC中,∠ACB=90o ,CD平分∠ACB, DE⊥BC,DF⊥AC ,垂足分别为E,F .求证:四边形CFDE是正方形. 分析:要证明四边形CFDE是正方形,可先证CFDE是矩形,然后再证有一组邻边相等;也可以先证四边形CFDE是菱形,然后再证有一个角是直角. 引导引导证明:∵ CD平分∠ACB,DE⊥BC,DF⊥AC,∴ DE=DF.∵ ∠DEC=∠ECF=∠CFD=90°,∴ 四边形CFDE是矩形.∵ DE=DF,∴ 四边形CFDE是正方形. 例6 如图所示,在△ABC中,∠ACB=90o ,CD平分∠ACB, DE⊥BC,DF⊥AC ,垂足分别为E,F .求证:四边形CFDE是正方形.交流讨论: 从一张彩纸上剪出一个正方形,你能检验剪出的图形符合要求吗?你是如何检验的,与同伴交流一下.引导回顾正方形的性质和判定方法.小结 写一篇关于对正方形及我们已经学习过的其他特殊四边形认识的小论文. (友情提示:可以从体现它们一般与特殊关系的性质入手,也可以专门从判定正方形的方法入手)作业谢谢 !
