17.5 一元二次方程的应用(2)同步练习
文档属性
| 名称 | 17.5 一元二次方程的应用(2)同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 410.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-04 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
17.5 一元二次方程的应用(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.数字问题的数量关系:(1)一个两位数,个位数字是a,十位数字是b,则两位数可表示为 10b+a .
(2)一个三位数,个位数字是a,十位数字是b,百位数字是c,可表示为100c+10b+a
2.行程问题中的数量关系:路程=速度×时间.
3.面积问题中的数量关系:矩形的面积=长×宽 .
基础知识和能力拓展精练
一、选择题
1.从正方形铁片上截去宽的一个矩形,剩余矩形的面积为,则原来正方形的面积为( ).
A. B. C. D.
2.如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设a=1,则b=( )
A. B. C. D.
3.三角形两边的长分别是8和6,第三边的长是一元二次方程x2﹣16x+60=0的一个实数根,则该三角形的面积是( )
A. 24 B. 24或8 C. 48 D. 8
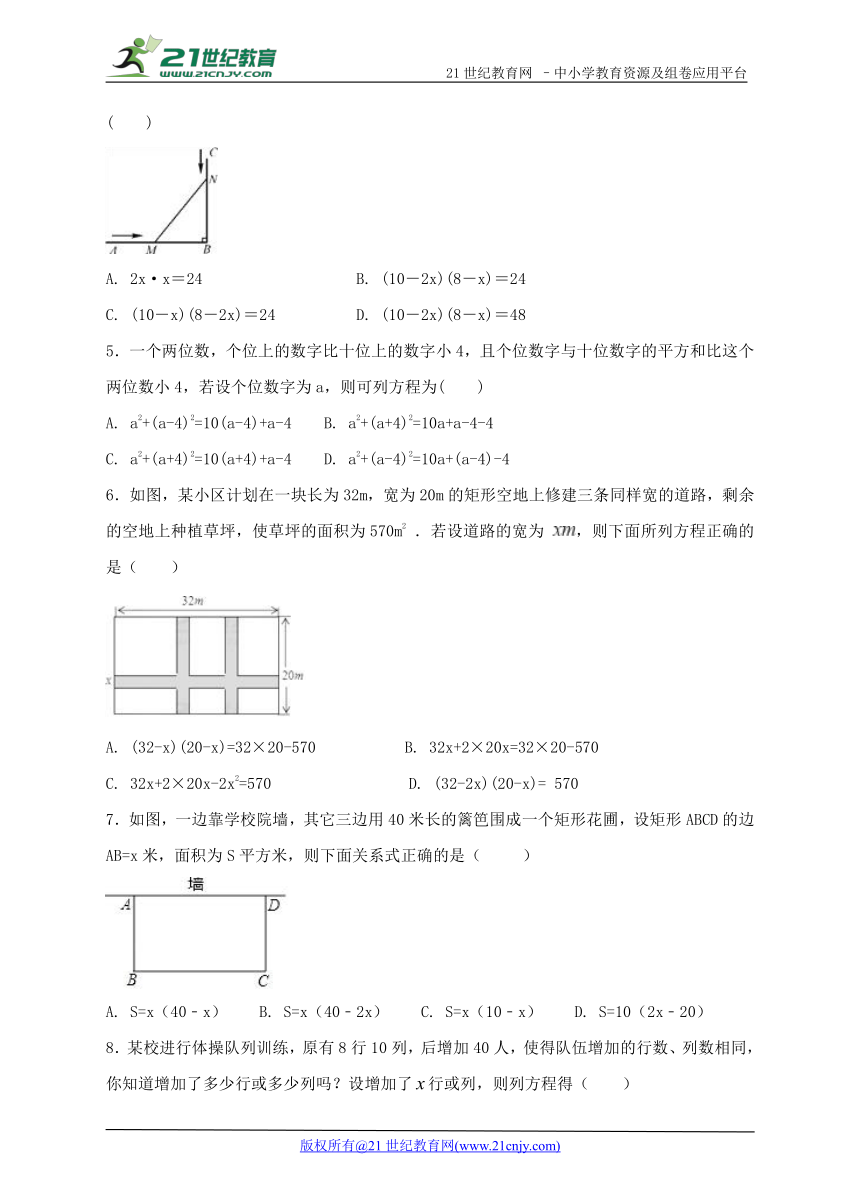
4.如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm2,由题意可列方程( )
A. 2x·x=24 B. (10-2x)(8-x)=24
C. (10-x)(8-2x)=24 D. (10-2x)(8-x)=48
5.一个两位数,个位上的数字比十位上的数字小4,且个位数字与十位数字的平方和比这个两位数小4,若设个位数字为a,则可列方程为( )
A. a2+(a-4)2=10(a-4)+a-4 B. a2+(a+4)2=10a+a-4-4
C. a2+(a+4)2=10(a+4)+a-4 D. a2+(a-4)2=10a+(a-4)-4
6.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 .若设道路的宽为 ,则下面所列方程正确的是( )
A. (32-x)(20-x)=32×20-570 B. 32x+2×20x=32×20-570
C. 32x+2×20x-2x2=570 D. (32-2x)(20-x)= 570
7.如图,一边靠学校院墙,其它三边用40米长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=x米,面积为S平方米,则下面关系式正确的是( )
A. S=x(40﹣x) B. S=x(40﹣2x) C. S=x(10﹣x) D. S=10(2x﹣20)
8.某校进行体操队列训练,原有8行10列,后增加40人,使得队伍增加的行数、列数相同,你知道增加了多少行或多少列吗?设增加了行或列,则列方程得( )
A. (8﹣) (10﹣)=8×10﹣40 B. (8﹣)(10﹣)=8×10+40
C. (8+ )(10+ )=8×10﹣40 D. (8+ )(10+ )=8×10+40
二、填空题
9.一包洽洽瓜子售价8元,商家为了促销,顾客每买一包洽洽瓜子获一张奖券,每4张奖券可兑换一包洽洽瓜子,则每张奖券相当于______元.
10.某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查发现,售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个.为实现平均每月10000元的销售利润,则这种台灯的售价应定为___元.
11.如图,在Rt△ABC中,∠B=90°,AB=6 cm,BC=8 cm,点P从A点开始沿AB边向点B以1 cm/s的速度移动,点Q从B点开始沿BC边向点C以2 cm/s的速度移动,则P、Q分别从A、B同时出发,经过________秒钟,使△PBQ的面积等于8 cm2.
12.一超市销售某种品牌的牛奶,进价为每盒1.5元,售价为每盒2.2元时,每天可售5000盒,经过调查发现,若每盒降价0.1元,则可多卖2000盒。要使每天盈利4500元,该超市定价为_________元。
三、解答题
13.已知一个两位数,个位上的数字比十位上的数字少4,这个两位数十位和个位交换位置后,新两位数与原两位数的积为1612,求这个两位数.
14.如图,在长为20cm,宽为16cm的矩形的四个角上截去四个全等的小正方形,使得剩下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去的小正方形的边长.
15.一个醉汉拿着一根竹竿进城,横着怎么也拿不进去,量竹竿长比城门宽4米,旁边一个醉汉嘲笑他,你没看城门高吗,竖着拿就可以进去啦,结果竖着比城门高2米,二人没办法,只好请教聪明人,聪明人教他们二人沿着门的对角斜着拿,二人一试,不多不少刚好进城,你知道竹竿有多长吗?
16.万达旅行社为吸引市民组团去黄山风景区旅游,推出了如下的收费标准:
宿州高铁新区组织员工去黄山风景区旅游,共支付给万达旅行社旅游费用27 000元,请问该单位这次共有多少员工去黄山风景区旅游?
17.某市计划举办青少年足球比赛,赛制采取双循环形式(即每两队之间都要打两场比赛),一共组织30场比赛.计分规则为胜一场得3分,平一场得1分,负一场得0分.
(1)该市举办方应该邀请多少支球队参赛?
(2)此次比赛结束后,如果其中一支参赛球队共平了4场,负了2场,则该球队此次比赛的总积分是多少?
18.如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,
(1)如果P、Q同时出发,几秒后,可使△PBQ的面积为8平方厘米?
(2)线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
参考答案
1.A
【解析】设正方形的边长为xcm,由题意得
x(x-2)=80,
解之得
x1=10,x2=-8(舍去).
∴原来正方形的面积为:10×10=100(cm2).
故选A.
2.B
【解析】依题意得(a+b)2=b(b+a+b),
而a=1,
∴b2﹣b﹣1=0,
∴ ,而b不能为负,
∴.
故选B.
点睛:根据左图可以知道图形是一个正方形,边长为(a+b),右图是一个长方形,长宽分别为(b+a+b)、b,并且它们的面积相等,由此即可列出等式(a+b)2=b(b+a+b),而a=1,代入即可得到关于b的方程,解方程即可求出b.
3.B
【解析】试题解析: (x 6)(x 10)=0,
∴x=6或x=10.
当x=6时,该三角形为以6为腰,8为底的等腰三角形,
∴高
当x=10时,该三角形为以6和8为直角边,10为斜边的直角三角形,
∴S=24或.
故选B.
4.D
【解析】设x秒后,螳螂走了 2x,蝉走了x,MB=10-2x,NC=8-x,
由题意知 EMBED Equation.DSMT4 (10-2x)(8-x)=24,
(10-2x)(8-x)=48,选D.
5.C
【解析】依题意得:十位数字为:a+4,这个数为:a+10(x+4),
这两个数的平方和为:a2+(a+4)2,
∵两数相差4,
∴a2+(a+4)2=10(a+4)+a 4.
故选:C.
点睛:本题考查了数的表示方法,要会用未知数表示两位数,然后根据题意列出对应的方程求解.
6.D
【解析】通过平移可将六块草坪拼为一块,可得一个大矩形,由图易得该矩形的长为(32 2x)m,宽为(20-x)m,由此根据题意可得:
( 32 2 x ) ( 20 x ) = 570.
故选D.
7.B
【解析】AB=x米,面积为S平方米,
S=x(40﹣2x).
故选B.
8.D
【解析】增加了行或列,现在是行, 列,所以(8+ )(10+ )=8×10+40.
9.1.6
【解析】试题解析:解:设每张奖券相当于x元,根据题意得:
4×8=5(8﹣x),解得:x=1.6.
故答案为:1.6.
点睛:考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,由售价找出合适的等量关系,列出方程,再求解.
10.50
【解析】设这种台灯的售价应定为每台元,根据题意可得:
化简、整理得: ,解得: .
又∵,
∴,即这种台灯售价应定为每台50元.
11.2或4
【解析】设x秒时.由三角形的面积公式列出关于x的方程,
(6-x) 2x=8,
通过解方程求得x1=2,x2=4;
故答案为2或4.
12.2或1.95元
【解析】设每盒降价x元,
(2.2-1.5-x)(5000+2000)=4500,
20x2-9x+1=0,
(4x-1)(5x-1)=0,
x1=0.25, x2=0.2,
当x=0.25时,2.2-x=2.2-0.25=1.95,
当x=0.2时,2.2-x=2.2-0.2=2,
所以定价为1.95元或2元,
故答案为:1.95或2.
【点睛】本题考查了一元二次方程的应用,首先要正确理解题意,把实际问题的数量关系转化为一元二次方程求解.
13.62.
【解析】试题分析:首先根据“个位上的数字比十位上的数字少4”这句话设十位数字为x,则个位数字为x-4,分别表示出原来的两位数和个位、十位交换后的两位数,列方程求解.
试题解析:解:设原数十位数字为x,个位数字为(x-4),则原数为10x+(x-4);交换位置后新数为10(x-4)+x.由题意得[10x+(x-4)]×[10(x-4)+x]=1612,整理得x2-4x-12=0,解得x1=6,x2=-2.数字-2不合题意,应舍去,∴x=6,x-4=2,∴原来这个两位数是62.
点睛:若个位上数字为a,十位上数字为b,则这个两位数为:10b+a.
14.小正方形的边长为.
【解析】试题分析:等量关系为:矩形面积-四个全等的小正方形面积=矩形面积×80%,列方程即可求解.
试题解析:设小正方形的边长为xcm,根据题意得:
20×16- ,
解得: ,
为正数,
∴ ,
答:小正方形的边长为.
15.这根竹竿长为10米.
【解析】试题分析:如图,恰好构成直角三角形三边,利用勾股定理可求竹竿长.
试题解析:
设竹竿的长为x米,由题意可得方程:
,
整理得: ,
解这个方程得:x1=10, x2=2 (舍去).
答:这根竹竿长为10米.
16.30名
【解析】试题分析:由题意易得人数超过了25人,那么关系式为:[1000-(劳模人数-25)×20]×劳模人数=27000.由此列方程求解即可.
试题解析:设该单位这次共有x名员工去黄山风景区旅游.因为1 000×25=25 000<27 000,所以员工人数一定超过25人,可得方程[1 000-20(x-25)]x=27 000,
整理得x2-75x+1 350=0,
解得x1=45,x2=30.
当x1=45时,1 000-20(x-25)=600<700,故舍去x1;
当x2=30时,1 000-20(x-25)=900>700,符合题意.
答:该单位这次共有30名员工去黄山风景区旅游
17.(1)该市举办方应邀请6支球队参赛;
(2)该市举办方应邀请6支球队参赛,该球队的总积分为16分。
【解析】⑴设该市举办方应邀请支球队参赛
依题意得,
解方程得,
(2)16
答:该市举办方应邀请6支球队参赛,该球队的总积分为16分。
18.(1)2秒或4秒;(2)线段PQ不能否将△ABC分成面积相等的两部分.
【解析】试题分析:(1)设出运动所求的时间,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;
(2)将△PBQ的面积表示出来,根据△=b2-4ac来判断.
试题解析:(1)设经过x秒,使△PBQ的面积等于8cm2,依题意有:
(6-x) 2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意,
故经过2秒或4秒,△PBQ的面积等于8cm2;
(2)不能,理由如下:
设经过y秒,线段PQ能将△ABC分成面积相等的两部分,依题意有:
S△ABC =×6×8=24,
(6﹣y) 2y=12,
y2﹣6y+12=0,
∵△=b2﹣4ac=36﹣4×12=﹣12<0,
∴此方程无实数根,
∴线段PQ不能否将△ABC分成面积相等的两部分.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
17.5 一元二次方程的应用(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.数字问题的数量关系:(1)一个两位数,个位数字是a,十位数字是b,则两位数可表示为 10b+a .
(2)一个三位数,个位数字是a,十位数字是b,百位数字是c,可表示为100c+10b+a
2.行程问题中的数量关系:路程=速度×时间.
3.面积问题中的数量关系:矩形的面积=长×宽 .
基础知识和能力拓展精练
一、选择题
1.从正方形铁片上截去宽的一个矩形,剩余矩形的面积为,则原来正方形的面积为( ).
A. B. C. D.
2.如图,若将左图正方形剪成四块,恰能拼成右图的矩形,设a=1,则b=( )
A. B. C. D.
3.三角形两边的长分别是8和6,第三边的长是一元二次方程x2﹣16x+60=0的一个实数根,则该三角形的面积是( )
A. 24 B. 24或8 C. 48 D. 8
4.如图,AB⊥BC,AB=10 cm,BC=8 cm,一只蝉从C点沿CB方向以每秒1 cm的速度爬行,蝉开始爬行的同时,一只螳螂由A点沿AB方向以每秒2 cm的速度爬行,当螳螂和蝉爬行x秒后,它们分别到达了M,N的位置,此时,△MNB的面积恰好为24 cm2,由题意可列方程( )
A. 2x·x=24 B. (10-2x)(8-x)=24
C. (10-x)(8-2x)=24 D. (10-2x)(8-x)=48
5.一个两位数,个位上的数字比十位上的数字小4,且个位数字与十位数字的平方和比这个两位数小4,若设个位数字为a,则可列方程为( )
A. a2+(a-4)2=10(a-4)+a-4 B. a2+(a+4)2=10a+a-4-4
C. a2+(a+4)2=10(a+4)+a-4 D. a2+(a-4)2=10a+(a-4)-4
6.如图,某小区计划在一块长为32m,宽为20m的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪,使草坪的面积为570m2 .若设道路的宽为 ,则下面所列方程正确的是( )
A. (32-x)(20-x)=32×20-570 B. 32x+2×20x=32×20-570
C. 32x+2×20x-2x2=570 D. (32-2x)(20-x)= 570
7.如图,一边靠学校院墙,其它三边用40米长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=x米,面积为S平方米,则下面关系式正确的是( )
A. S=x(40﹣x) B. S=x(40﹣2x) C. S=x(10﹣x) D. S=10(2x﹣20)
8.某校进行体操队列训练,原有8行10列,后增加40人,使得队伍增加的行数、列数相同,你知道增加了多少行或多少列吗?设增加了行或列,则列方程得( )
A. (8﹣) (10﹣)=8×10﹣40 B. (8﹣)(10﹣)=8×10+40
C. (8+ )(10+ )=8×10﹣40 D. (8+ )(10+ )=8×10+40
二、填空题
9.一包洽洽瓜子售价8元,商家为了促销,顾客每买一包洽洽瓜子获一张奖券,每4张奖券可兑换一包洽洽瓜子,则每张奖券相当于______元.
10.某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查发现,售价在40元至60元范围内,这种台灯的售价每上涨1元,其销售量就将减少10个.为实现平均每月10000元的销售利润,则这种台灯的售价应定为___元.
11.如图,在Rt△ABC中,∠B=90°,AB=6 cm,BC=8 cm,点P从A点开始沿AB边向点B以1 cm/s的速度移动,点Q从B点开始沿BC边向点C以2 cm/s的速度移动,则P、Q分别从A、B同时出发,经过________秒钟,使△PBQ的面积等于8 cm2.
12.一超市销售某种品牌的牛奶,进价为每盒1.5元,售价为每盒2.2元时,每天可售5000盒,经过调查发现,若每盒降价0.1元,则可多卖2000盒。要使每天盈利4500元,该超市定价为_________元。
三、解答题
13.已知一个两位数,个位上的数字比十位上的数字少4,这个两位数十位和个位交换位置后,新两位数与原两位数的积为1612,求这个两位数.
14.如图,在长为20cm,宽为16cm的矩形的四个角上截去四个全等的小正方形,使得剩下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去的小正方形的边长.
15.一个醉汉拿着一根竹竿进城,横着怎么也拿不进去,量竹竿长比城门宽4米,旁边一个醉汉嘲笑他,你没看城门高吗,竖着拿就可以进去啦,结果竖着比城门高2米,二人没办法,只好请教聪明人,聪明人教他们二人沿着门的对角斜着拿,二人一试,不多不少刚好进城,你知道竹竿有多长吗?
16.万达旅行社为吸引市民组团去黄山风景区旅游,推出了如下的收费标准:
宿州高铁新区组织员工去黄山风景区旅游,共支付给万达旅行社旅游费用27 000元,请问该单位这次共有多少员工去黄山风景区旅游?
17.某市计划举办青少年足球比赛,赛制采取双循环形式(即每两队之间都要打两场比赛),一共组织30场比赛.计分规则为胜一场得3分,平一场得1分,负一场得0分.
(1)该市举办方应该邀请多少支球队参赛?
(2)此次比赛结束后,如果其中一支参赛球队共平了4场,负了2场,则该球队此次比赛的总积分是多少?
18.如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,
(1)如果P、Q同时出发,几秒后,可使△PBQ的面积为8平方厘米?
(2)线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
参考答案
1.A
【解析】设正方形的边长为xcm,由题意得
x(x-2)=80,
解之得
x1=10,x2=-8(舍去).
∴原来正方形的面积为:10×10=100(cm2).
故选A.
2.B
【解析】依题意得(a+b)2=b(b+a+b),
而a=1,
∴b2﹣b﹣1=0,
∴ ,而b不能为负,
∴.
故选B.
点睛:根据左图可以知道图形是一个正方形,边长为(a+b),右图是一个长方形,长宽分别为(b+a+b)、b,并且它们的面积相等,由此即可列出等式(a+b)2=b(b+a+b),而a=1,代入即可得到关于b的方程,解方程即可求出b.
3.B
【解析】试题解析: (x 6)(x 10)=0,
∴x=6或x=10.
当x=6时,该三角形为以6为腰,8为底的等腰三角形,
∴高
当x=10时,该三角形为以6和8为直角边,10为斜边的直角三角形,
∴S=24或.
故选B.
4.D
【解析】设x秒后,螳螂走了 2x,蝉走了x,MB=10-2x,NC=8-x,
由题意知 EMBED Equation.DSMT4 (10-2x)(8-x)=24,
(10-2x)(8-x)=48,选D.
5.C
【解析】依题意得:十位数字为:a+4,这个数为:a+10(x+4),
这两个数的平方和为:a2+(a+4)2,
∵两数相差4,
∴a2+(a+4)2=10(a+4)+a 4.
故选:C.
点睛:本题考查了数的表示方法,要会用未知数表示两位数,然后根据题意列出对应的方程求解.
6.D
【解析】通过平移可将六块草坪拼为一块,可得一个大矩形,由图易得该矩形的长为(32 2x)m,宽为(20-x)m,由此根据题意可得:
( 32 2 x ) ( 20 x ) = 570.
故选D.
7.B
【解析】AB=x米,面积为S平方米,
S=x(40﹣2x).
故选B.
8.D
【解析】增加了行或列,现在是行, 列,所以(8+ )(10+ )=8×10+40.
9.1.6
【解析】试题解析:解:设每张奖券相当于x元,根据题意得:
4×8=5(8﹣x),解得:x=1.6.
故答案为:1.6.
点睛:考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,由售价找出合适的等量关系,列出方程,再求解.
10.50
【解析】设这种台灯的售价应定为每台元,根据题意可得:
化简、整理得: ,解得: .
又∵,
∴,即这种台灯售价应定为每台50元.
11.2或4
【解析】设x秒时.由三角形的面积公式列出关于x的方程,
(6-x) 2x=8,
通过解方程求得x1=2,x2=4;
故答案为2或4.
12.2或1.95元
【解析】设每盒降价x元,
(2.2-1.5-x)(5000+2000)=4500,
20x2-9x+1=0,
(4x-1)(5x-1)=0,
x1=0.25, x2=0.2,
当x=0.25时,2.2-x=2.2-0.25=1.95,
当x=0.2时,2.2-x=2.2-0.2=2,
所以定价为1.95元或2元,
故答案为:1.95或2.
【点睛】本题考查了一元二次方程的应用,首先要正确理解题意,把实际问题的数量关系转化为一元二次方程求解.
13.62.
【解析】试题分析:首先根据“个位上的数字比十位上的数字少4”这句话设十位数字为x,则个位数字为x-4,分别表示出原来的两位数和个位、十位交换后的两位数,列方程求解.
试题解析:解:设原数十位数字为x,个位数字为(x-4),则原数为10x+(x-4);交换位置后新数为10(x-4)+x.由题意得[10x+(x-4)]×[10(x-4)+x]=1612,整理得x2-4x-12=0,解得x1=6,x2=-2.数字-2不合题意,应舍去,∴x=6,x-4=2,∴原来这个两位数是62.
点睛:若个位上数字为a,十位上数字为b,则这个两位数为:10b+a.
14.小正方形的边长为.
【解析】试题分析:等量关系为:矩形面积-四个全等的小正方形面积=矩形面积×80%,列方程即可求解.
试题解析:设小正方形的边长为xcm,根据题意得:
20×16- ,
解得: ,
为正数,
∴ ,
答:小正方形的边长为.
15.这根竹竿长为10米.
【解析】试题分析:如图,恰好构成直角三角形三边,利用勾股定理可求竹竿长.
试题解析:
设竹竿的长为x米,由题意可得方程:
,
整理得: ,
解这个方程得:x1=10, x2=2 (舍去).
答:这根竹竿长为10米.
16.30名
【解析】试题分析:由题意易得人数超过了25人,那么关系式为:[1000-(劳模人数-25)×20]×劳模人数=27000.由此列方程求解即可.
试题解析:设该单位这次共有x名员工去黄山风景区旅游.因为1 000×25=25 000<27 000,所以员工人数一定超过25人,可得方程[1 000-20(x-25)]x=27 000,
整理得x2-75x+1 350=0,
解得x1=45,x2=30.
当x1=45时,1 000-20(x-25)=600<700,故舍去x1;
当x2=30时,1 000-20(x-25)=900>700,符合题意.
答:该单位这次共有30名员工去黄山风景区旅游
17.(1)该市举办方应邀请6支球队参赛;
(2)该市举办方应邀请6支球队参赛,该球队的总积分为16分。
【解析】⑴设该市举办方应邀请支球队参赛
依题意得,
解方程得,
(2)16
答:该市举办方应邀请6支球队参赛,该球队的总积分为16分。
18.(1)2秒或4秒;(2)线段PQ不能否将△ABC分成面积相等的两部分.
【解析】试题分析:(1)设出运动所求的时间,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;
(2)将△PBQ的面积表示出来,根据△=b2-4ac来判断.
试题解析:(1)设经过x秒,使△PBQ的面积等于8cm2,依题意有:
(6-x) 2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意,
故经过2秒或4秒,△PBQ的面积等于8cm2;
(2)不能,理由如下:
设经过y秒,线段PQ能将△ABC分成面积相等的两部分,依题意有:
S△ABC =×6×8=24,
(6﹣y) 2y=12,
y2﹣6y+12=0,
∵△=b2﹣4ac=36﹣4×12=﹣12<0,
∴此方程无实数根,
∴线段PQ不能否将△ABC分成面积相等的两部分.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
