3.1用表格表示的变量间关系 教学课件

课件21张PPT。3.1用表格表示的变量间关系第三章 变量之间的关系 万物都在悄悄地发生着变化，从数学的角度研究它们之间的关系，将有助于我们更好地认识世界，预测未来，那就让我们一起来揭开变化的新篇章吧…情境引入
你能从生活中举出一些发生变化的例子吗？烧一壶水，十分钟后水开了。在这一过程中，什么在发生变化？
情境引入看图回答
1．你能大致描述男女平均身高的变化情况吗？
2．你的身高在平均身高之上还是之下？
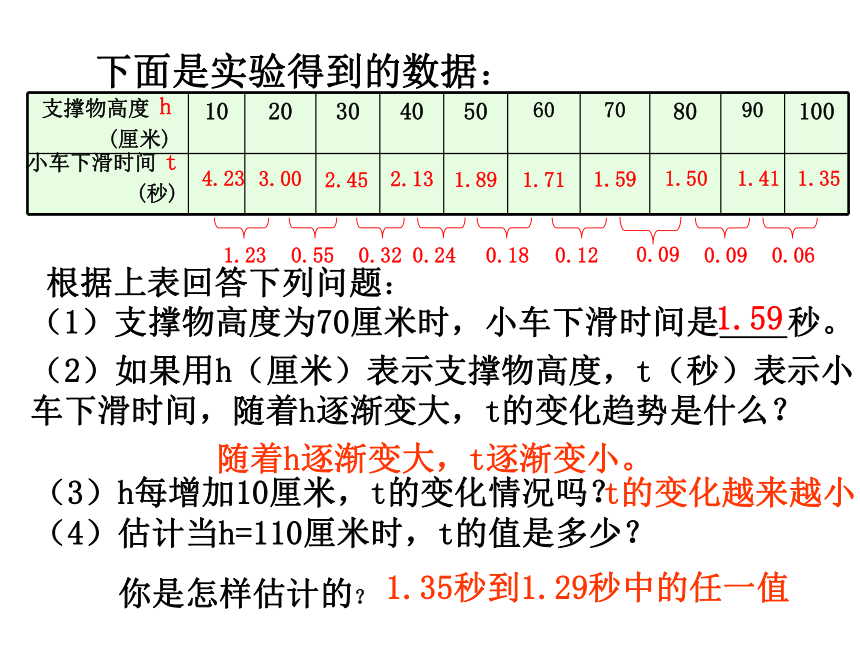
3．你能估计自己十八岁的身高吗？ 新知探究仔细观察：小车的运动200406080100单位:cm细心体会下面是实验得到的数据：（1）支撑物高度为70厘米时，小车下滑时间是 秒。 （2）如果用h（厘米）表示支撑物高度，t（秒）表示小车下滑时间，随着h逐渐变大，t的变化趋势是什么？（3）h每增加10厘米，t的变化情况吗？（4）估计当h=110厘米时，t的值是多少？
你是怎样估计的？4.231.351.411.501.591.711.892.132.453.00根据上表回答下列问题： 支撑物高度
(厘米)小车下滑时间
(秒)ht1.59随着h逐渐变大，t逐渐变小。t的变化越来越小1.35秒到1.29秒中的任一值（5）随着支撑物高度h的变化，还有哪些量发生变化？哪些量始终不发生变化？
议一议：
我国从1949年到2009年的人口统计数据如下（精确到0.01亿）:（1）如果用x表示时间，y表示我国人口总数，那么随着x的变化，y的变化趋势是什么？（2）从1949年起，时间每向后推移10年，我国人口是怎样变化的？ 在表一中，支撑物的高度h和小车下滑的时间t都在变化，它们都是变量(variable).其中小车下滑的时间t随支撑物的高度h的变化而变化.支撑物的高度h是自变量(independent variale)，小车下滑的时间t是因变量(dependent variale).
领悟概念: 在这一变化过程中，小车下滑的距离（木板的长度）一直没有变化.像这种在变化过程中数值始终不变的量叫做常量（constant）.
在表2中，我国人口总数y随着x的变化而变化，其中x是_______，y是______.自变量因变量 在“儿童从出生到10岁的体重变化”中，儿童的体重随年龄的变化而变化.年龄是自变量，体重是因变量.
借助表格，我们可以表示因变量随自变量的变化而变化的情况.
在表格里，通常把自变量放在上（或左）面，把因变量放在下（或右）面.
解析被动变化的量在变化过程中，若有两个变量x和y, 其中y随着x 的变化而发生变化，我们就把x叫自变量，y叫因变量。
1.自变量是在一定范围内主动变化的量。2.因变量是随自变量变化而变化的量。3.表格可以表示因变量随自变量变化而变化的情
况，还能帮助我们对变化趋势进行初步的预测。因变量自变量主动变化的量变量 你早晨从家到学校，在这个过程中，哪些是变量，哪些是自变量，哪些是因变量？我 能 行:阅读完两个表格，你有哪些感想？表二：根据国家统计局对于全海域海水水质评价结果的统计，较清洁海域面积在2003至2010年间的变化情况如下表：
保护环境人人有责表一：国家统计局对于2003年至2010年我国的环境污染治理投资费用的统计见下表： 1、 生活中有哪些例子反映了变量之间的关系？与同伴进行交流. 畅所欲言(1)上表反映了哪两个变量之间的关系？哪个是
自变量？哪个是因变量？
(2)当氮肥的施用量是101千克/公顷时，土豆的
产量是多少？如果不施氮肥呢？2．研究表明，当钾肥和磷肥的施用量一定时，
土豆的产量与氮肥的施用量有如下关系：2．研究表明，当钾肥和磷肥的施用量一定时，
土豆的产量与氮肥的施用量有如下关系：（3）根据表格中的数据，你认为氮肥的施用量是多少时比较适宜？说说你的理由.
(4)粗略说一说氮肥的施用量对土豆产量的影响.
研究表明，当钾肥和磷肥的施用量一定时，土豆的产量与氮肥的施用量有如下关系： (1)上表反映了哪两个变量之间的关系？
是自变量, 是因变量.(3)根据表格，你认为氮肥的施用量是
时比较适宜？说说你的理由。(4)粗略说一说氮肥的施用量对土豆产量的影响。氮肥施用量(2)当氮肥的施用量是101千克/公顷时，土豆的产量是 吨/公顷,如果不施氮肥呢？ 32.2915.18吨/公顷土豆产量 通过本节课的学习，你学到了什么？有什么收获？还有那些问题需要我们共同解决，请提出来。 1．举例说明你是怎样理解变量、自变量、因变量的？
2．学会应用表格表示变量之间的关系。
3．能从表格中获取变量之间的关系的信息，并且能根据获取的信息初步进行预测。
4．谈谈你的收获与困惑。 知识梳理上网费包括网络使用费（每月38元）和上网通信费（每小时2元），某电信局对拨号上网用户实行分时段优惠，具体优惠政策如下表（包括最大值，不包括最小值）：你能根据左边提供的例子完成下表吗？教材 习题§4.1随堂练习家庭实验：
点燃一支蜡烛，记录蜡烛
的长度和燃烧时间（每3分钟）
之间的关系.