平面图形的认识(二)综合培优试题(无答案)
文档属性
| 名称 | 平面图形的认识(二)综合培优试题(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 315.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-05 00:00:00 | ||
图片预览


文档简介
平面图形的认识(二)综合培优
1.若△ABC的三边长分别为整数,周长为11,且有一边长为4,则这个三角形的最大边长为
2.如图,若AB∥CD,则∠A、∠E、∠D之间的关系是
3.(2013.河南)将一副直角三角板ABC和DEF按如图所示方式放置(其中∠A=60°,∠F=45°),若使点E落在边AC上,且ED∥BC,则∠CEF=_______
4.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为
5.满足下列条件的△ABC中,不是直角三角形的是 ( ). A.∠A+∠B=∠C B.∠A:∠B:∠C=2:3:1 C.∠A=2∠B=3∠C D.一个外角等于和它相邻的内角
6.如图,两平面镜、的夹角为,入射光线AO平行于入射到上,经两次反射后的出射光线O′R平行于,则角等于_________度.
第18题 第19题
7.(1)如图,已知∠ABE=142°,∠C=72°,则∠A=________,∠ABC=________.
(2).一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是( )
△ABC中,∠A=∠B=∠C,则△ABC是_______三角形.
8. 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是_______.
9 如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF//AD,FN∥DC,则∠B=_______°.
10.若两个角的两边分别平行,且其中一个角比另一个角的2倍少30°,则这两个角分别为______________.
11.如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠B=50°,则∠BDF=_______°.
12.光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的入射 角等于反射角,即∠1=∠6,∠5=∠3,∠2=∠4.若已知∠1=55°,∠3=75°,那么∠2=_______度.
13.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80°,则∠BFD=_______.
14.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:
(1)∠EDC的度数;
(2)若∠BCD=n°,试求∠BED的度数.
15.已知,如图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
(1)若∠B=40°,∠C=30°,则∠DAE=_______;
(2)若∠B=80°,∠C=40°,则∠DAE=_______;
(3)由(1)、(2)我能猜想出∠DAE与∠B、∠C之间的关系为______________,并说明理由.
16.(1)如图,小莉画了一个角∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.
试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.
(2)聪明的小莉想出了一个画30°角的方法:①画两条相交的直线OX、OY,使∠XOY=60°,②在射线OX、OY上分别再任意取A、B点,③作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,则∠C就是30°的角.你认为小莉的方法正确吗?请你说明理由.
17.如图1,一个三角形的纸片ABC.点D,E分别是△ABC边上的两点.
研究(1):如果沿直线DE折叠,则∠BDA'与∠A的关系是______________,
研究(2):如果折成图2的形状.猜想∠BDA',∠CEA'和∠A的关系.并说明理由;
研究(3):如果折成图3的形状,猜想∠BDA',∠CEA'和∠A的关系,并说明理由.
18.(2013.湘西)如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,若∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是
19.光线以如图所示的角度α照射到平面镜工上,然后在平面镜I,Ⅱ之间来回反射.若∠α=50°,∠β=60°,则∠γ等于
20.若用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为_______°.
21.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P.若 ∠BPC=40°,则∠CAP=_______.
22.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中a称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为_______.
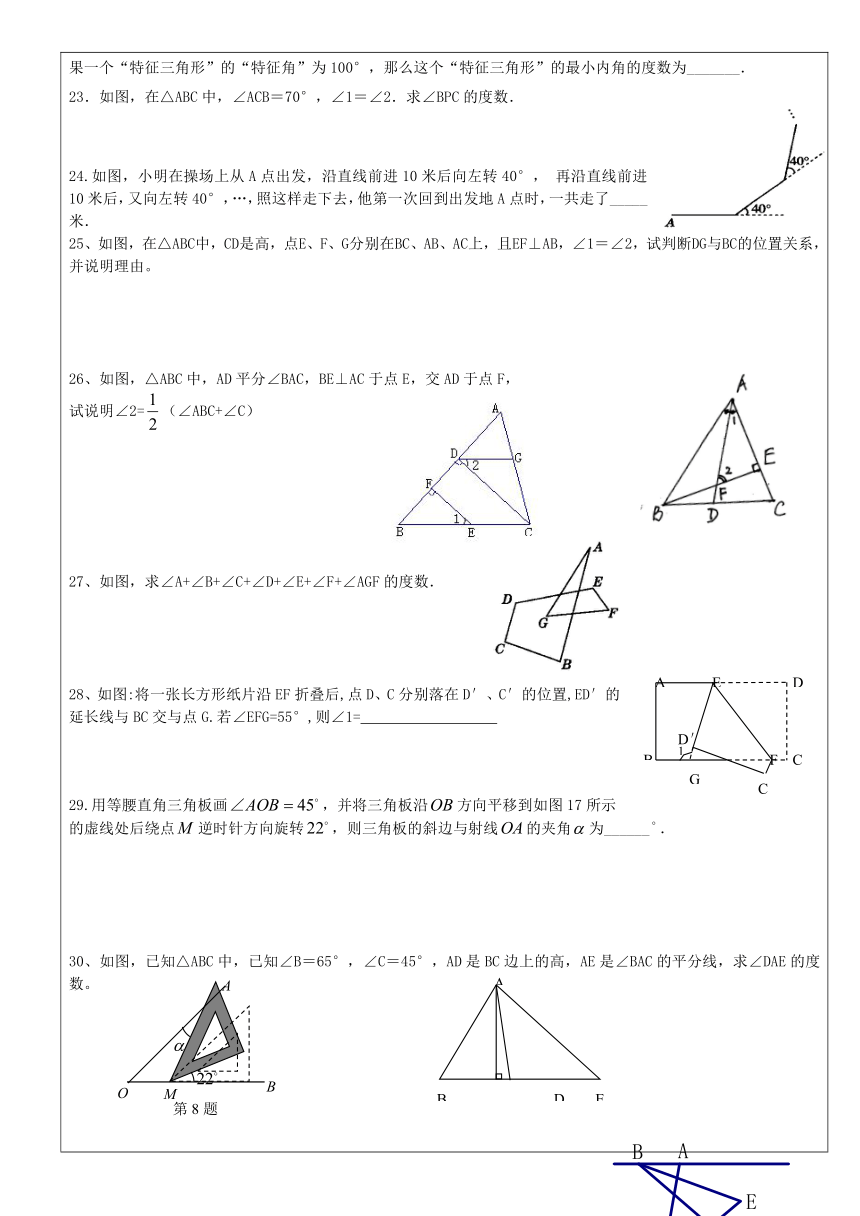
23.如图,在△ABC中,∠ACB=70°,∠1=∠2.求∠BPC的度数.
24.如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,…,照这样走下去,他第一次回到出发地A点时,一共走了_____米.
25、如图,在△ABC中,CD是高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由。
26、如图,△ABC中,AD平分∠BAC,BE⊥AC于点E,交AD于点F,
试说明∠2=(∠ABC+∠C)
27、如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠AGF的度数.
28、如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交与点G.若∠EFG=55°,则∠1=
29.用等腰直角三角板画,并将三角板沿方向平移到如图17所示的虚线处后绕点逆时针方向旋转,则三角板的斜边与射线的夹角为______.
30、如图,已知△ABC中,已知∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数。
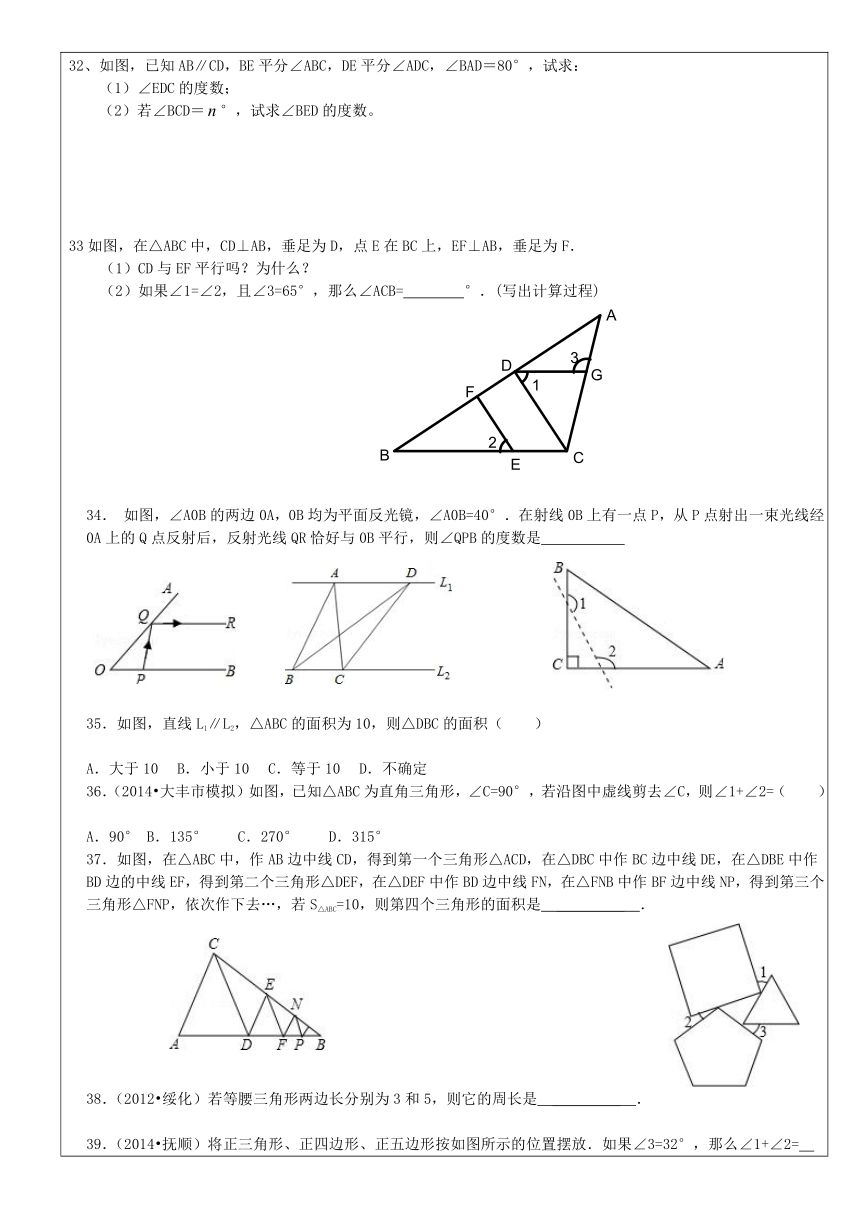
32、如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:
(1)∠EDC的度数;
(2)若∠BCD=°,试求∠BED的度数。
33如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=65°,那么∠ACB= °.(写出计算过程)
34. 如图,∠A0B的两边0A,0B均为平面反光镜,∠A0B=40°.在射线0B上有一点P,从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是
35.如图,直线L1∥L2,△ABC的面积为10,则△DBC的面积( )
A.大于10 B.小于10 C.等于10 D.不确定
36.(2014?大丰市模拟)如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=( )
A.90° B.135° C.270° D.315°
37.如图,在△ABC中,作AB边中线CD,得到第一个三角形△ACD,在△DBC中作BC边中线DE,在△DBE中作BD边的中线EF,得到第二个三角形△DEF,在△DEF中作BD边中线FN,在△FNB中作BF边中线NP,得到第三个三角形△FNP,依次作下去…,若S△ABC=10,则第四个三角形的面积是 _________ .
38.(2012?绥化)若等腰三角形两边长分别为3和5,则它的周长是 _________ .
39.(2014?抚顺)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2= _________ 度.
30.(2014?葫芦岛二模)如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2013BC的平分线与∠A2013CD的平分线交于点A2014,得∠A2014CD,则∠A2014= _________ .
41.如图:∠A+∠B+∠C+∠D+∠E+∠F等于 _________ 度.
42.(2013?邵阳)将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
43.如图(1)(2)(3)(4):AB∥CD,点P是一个动点,试探究:当点P在不同的位置时,请探索∠A,∠C,∠P之间的数量关系,请效图(2)推理填空,图(2)﹣(4)直接在横线上写出其数量关系.
(1)结论: _________ (2)结论: _________ (3)结论: _________ (4)结论: _________
(2)的推理过程如下:
解:过点P作PQ∥AB
则∠1=∠A( _________ )
∵PQ∥AB(已作)且AB∥CD( _________ )
∴EF∥CD( _________ )
∴∠2=∠C( _________ )
∵∠APC=∠1+∠2
∴∠APC=∠C+∠B( _________ )
44.(2014?顺义区二模)【问题】:如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB.若∠A=80°,则∠BEC= _________ ;若∠A=n°,则∠BEC= _________ .
【探究】:
(1)如图2,在△ABC中,BD、BE三等分∠ABC,CD、CE三等分∠ACB.若∠A=n°,则∠BEC= _________ ;
(2)如图3,在△ABC中,BE平分∠ABC,CE平分外角∠ACM.若∠A=n°,则∠BEC= _________ ;
(3)如图4,在△ABC中,BE平分外角∠CBM,CE平分外角∠BCN.若∠A=n°,则∠BEC= _________ .
45.(2012?樊城区模拟)下面是有关三角形内外角平分线的探究,阅读后按要求作答:?
探究1:如图(1),在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现:∠BOC=90°+∠A(不要求证明).
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的数量关系?请说明理由.?
探究3:如图(3)中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的数量关系?(只写结论,不需证明).结论: _________ .?
1.如图,l1∥l2.若∠2=2∠1,则∠1=_______,∠2=_______.
2.小明不小心将形状是梯形的玻璃打碎成两部分(如图).若量得上半部分的∠A=123°,∠D=104°,则原梯形玻璃下半部分的∠B=_______,∠C=_______.
3.如图,用吸管吮吸易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹角∠2=_______ .
4.如图,AB∥CD,∠A=35°,∠C=78°,则∠M=_______.
5.如图,CD平分∠ACB,DE∥BC,∠AED=80°,则∠EDC=_______.
6.如图,AB∥CD,∠BAE=40°,∠ECD=62°,EF平分∠AEC,则∠AEF=_______.
7.若—个多边形的每个外角都是72°,则这个多边形是_______边形,它的内角和为_______.
8.如图,已知△ABC的∠ABC和∠ACB的外角平分线交于点D,∠A=40°,则∠D=_______.
9.三角形两边的长分别为1和8.若该三角形第三边长为偶数,则该三角形的周长为_______.
10.如图,AB∥CD,直线MN与AB、CD分别交于E、F,GE⊥MN,∠1=130°,则∠2的度数为_______.
11.如图,等边三角形ABC沿边AB的方向平移到△BDE的位置,则图中∠CBE=_______,连接CE后,线段CE与AD的关系是_______.
12.如图,AB∥CD,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=_______.
13.如图,把△ABC平移到△DEF的位置,若AB=5 cm,则DE=_______;如果∠A=65°,∠B=30°,那么∠F=_______.
14.如图,把△ABC沿RS的方向平移到△DEF的位置,则AB∥_______,BC=_______;如果∠A=80°,那么∠D=_______.
15.如图,已知DE∥AB,∠ACD=75°,∠B=25°,则∠ACB的度数为_______.
二、选择题(每题2分,共22分)
16.经过平移,图形上的每个点都沿同一方向移动
了一定距离,下列说法中正确的是 ( )
A.不同的点移动的距离不同 B.不同的点移动的距离相同
C.不同的点移动的距离可能相同,也可能不同 D.无法确定
17.已知在△ABC中有两个角的大小分别为40°和70°,则这个三角形是 ( )
A.直角三角形 B.等边三角形 C钝角三角形 D.等腰三角形
19.下列角平分线中互相垂直的是 ( )
A.对顶角的平分线 B.两条平行线被第三条直线所截,内错角的平分线
C.两条平行线被第三条直线所截,同位角的平分线 D.两条平行线被第三条直线所截,同旁内角的平分线
20.已知等腰三角形的一个底角是30°,则这个三角形的顶角等于 ( )
A.150° B.120° C.75° D.30°
21.下列说法:①钝角三角形有两条高在三角形内部;②三角形的三条高最多有两条不在三角形内部;③三角形的三条高的交点不在三角形内部,就在三角形外部;④钝角三角形三个内角的平分线的交点一定不在三角形内部.其中正确的个数为 ( )A.1个 B.2个 C.3个 D.4个
23.下列叙述错误的是 ( )
A.△ABC中,∠A +∠B<∠C,此三角形不一定为钝角三角形
B.三角形可分为锐角三角形、直角三角形和钝角三角形
C.若三角形的一个外角小于与它相邻的一个内角,则这个三角形为钝角三角形
D.直角三角形只有一条高在三角形内
24.等腰三角形的一边长等于5,另一边长等于9,它的周长是 ( )
A.19 B.14 C.23 D.19或23
25.如图,∠1=∠2,∠DAB=∠BCD.给出下列结论:①AB∥DC;②AD∥BC;③∠B=∠D;④∠D=∠DAC.其中,正确的结论有 ( )A.1个 B.2个 C.3个 D.4个
26.如图,∠1+23=90°,∠2-∠3=90°,∠4=115°,那么23的度数是 ( )
A.45° B.65° C.60° D.75°
29.(5分)如图,AD∥BC,∠A=96°,∠D=104°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.
30.(6分)如图,AB∥CD,∠1:∠2:∠3=1:2:3.
(1)求∠3的度数;
(2)∠EBA与∠2相等吗?为什么?
31.(6分)如图,把一张长方形纸片ABCD沿EF折叠,C点落在C'处,D点落在D'处,ED'交BC于点G.已知∠EFG= 50°,试求∠DEG与∠BGD'的度数.
32.(6分)如图,AD⊥BC,EG⊥BC,垂足分别为D、G,∠E=∠AFE.试说明AD是△ABC的角平分线.
33.(7分)如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,你能求出∠B的度数吗?若能,请写出求解过程;若不能,请说明理由.
34.(8分)如图,O是△ABC的3条角平分线的交点,OG⊥BC,垂足为G.
(1)猜想∠BOC与90°+∠BAC之间的数量关系,并说明理由;
(2)∠DOB与∠GOC相等吗?为什么?
1.若△ABC的三边长分别为整数,周长为11,且有一边长为4,则这个三角形的最大边长为
2.如图,若AB∥CD,则∠A、∠E、∠D之间的关系是
3.(2013.河南)将一副直角三角板ABC和DEF按如图所示方式放置(其中∠A=60°,∠F=45°),若使点E落在边AC上,且ED∥BC,则∠CEF=_______
4.如图所示,将含有30°角的三角板的直角顶点放在相互平行的两条直线其中一条上,若∠1=35°,则∠2的度数为
5.满足下列条件的△ABC中,不是直角三角形的是 ( ). A.∠A+∠B=∠C B.∠A:∠B:∠C=2:3:1 C.∠A=2∠B=3∠C D.一个外角等于和它相邻的内角
6.如图,两平面镜、的夹角为,入射光线AO平行于入射到上,经两次反射后的出射光线O′R平行于,则角等于_________度.
第18题 第19题
7.(1)如图,已知∠ABE=142°,∠C=72°,则∠A=________,∠ABC=________.
(2).一个多边形截去一个角(不过顶点)后,形成的多边形的内角和是2520°,那么原多边形的边数是( )
△ABC中,∠A=∠B=∠C,则△ABC是_______三角形.
8. 如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转,CP与量角器的半圆弧交于点E,第24秒时,点E在量角器上对应的读数是_______.
9 如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF//AD,FN∥DC,则∠B=_______°.
10.若两个角的两边分别平行,且其中一个角比另一个角的2倍少30°,则这两个角分别为______________.
11.如图,把△ABC沿线段DE折叠,使点A落在点F处,BC∥DE,若∠B=50°,则∠BDF=_______°.
12.光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的入射 角等于反射角,即∠1=∠6,∠5=∠3,∠2=∠4.若已知∠1=55°,∠3=75°,那么∠2=_______度.
13.如图,若AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BED=80°,则∠BFD=_______.
14.如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:
(1)∠EDC的度数;
(2)若∠BCD=n°,试求∠BED的度数.
15.已知,如图,在△ABC中,∠B>∠C,AD是BC边上的高,AE平分∠BAC.
(1)若∠B=40°,∠C=30°,则∠DAE=_______;
(2)若∠B=80°,∠C=40°,则∠DAE=_______;
(3)由(1)、(2)我能猜想出∠DAE与∠B、∠C之间的关系为______________,并说明理由.
16.(1)如图,小莉画了一个角∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.
试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.
(2)聪明的小莉想出了一个画30°角的方法:①画两条相交的直线OX、OY,使∠XOY=60°,②在射线OX、OY上分别再任意取A、B点,③作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,则∠C就是30°的角.你认为小莉的方法正确吗?请你说明理由.
17.如图1,一个三角形的纸片ABC.点D,E分别是△ABC边上的两点.
研究(1):如果沿直线DE折叠,则∠BDA'与∠A的关系是______________,
研究(2):如果折成图2的形状.猜想∠BDA',∠CEA'和∠A的关系.并说明理由;
研究(3):如果折成图3的形状,猜想∠BDA',∠CEA'和∠A的关系,并说明理由.
18.(2013.湘西)如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,若∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是
19.光线以如图所示的角度α照射到平面镜工上,然后在平面镜I,Ⅱ之间来回反射.若∠α=50°,∠β=60°,则∠γ等于
20.若用等腰直角三角板画∠AOB=45°,并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°,则三角板的斜边与射线OA的夹角α为_______°.
21.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P.若 ∠BPC=40°,则∠CAP=_______.
22.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中a称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为_______.
23.如图,在△ABC中,∠ACB=70°,∠1=∠2.求∠BPC的度数.
24.如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,…,照这样走下去,他第一次回到出发地A点时,一共走了_____米.
25、如图,在△ABC中,CD是高,点E、F、G分别在BC、AB、AC上,且EF⊥AB,∠1=∠2,试判断DG与BC的位置关系,并说明理由。
26、如图,△ABC中,AD平分∠BAC,BE⊥AC于点E,交AD于点F,
试说明∠2=(∠ABC+∠C)
27、如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠AGF的度数.
28、如图:将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC交与点G.若∠EFG=55°,则∠1=
29.用等腰直角三角板画,并将三角板沿方向平移到如图17所示的虚线处后绕点逆时针方向旋转,则三角板的斜边与射线的夹角为______.
30、如图,已知△ABC中,已知∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数。
32、如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:
(1)∠EDC的度数;
(2)若∠BCD=°,试求∠BED的度数。
33如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=65°,那么∠ACB= °.(写出计算过程)
34. 如图,∠A0B的两边0A,0B均为平面反光镜,∠A0B=40°.在射线0B上有一点P,从P点射出一束光线经0A上的Q点反射后,反射光线QR恰好与0B平行,则∠QPB的度数是
35.如图,直线L1∥L2,△ABC的面积为10,则△DBC的面积( )
A.大于10 B.小于10 C.等于10 D.不确定
36.(2014?大丰市模拟)如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2=( )
A.90° B.135° C.270° D.315°
37.如图,在△ABC中,作AB边中线CD,得到第一个三角形△ACD,在△DBC中作BC边中线DE,在△DBE中作BD边的中线EF,得到第二个三角形△DEF,在△DEF中作BD边中线FN,在△FNB中作BF边中线NP,得到第三个三角形△FNP,依次作下去…,若S△ABC=10,则第四个三角形的面积是 _________ .
38.(2012?绥化)若等腰三角形两边长分别为3和5,则它的周长是 _________ .
39.(2014?抚顺)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=32°,那么∠1+∠2= _________ 度.
30.(2014?葫芦岛二模)如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2013BC的平分线与∠A2013CD的平分线交于点A2014,得∠A2014CD,则∠A2014= _________ .
41.如图:∠A+∠B+∠C+∠D+∠E+∠F等于 _________ 度.
42.(2013?邵阳)将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
43.如图(1)(2)(3)(4):AB∥CD,点P是一个动点,试探究:当点P在不同的位置时,请探索∠A,∠C,∠P之间的数量关系,请效图(2)推理填空,图(2)﹣(4)直接在横线上写出其数量关系.
(1)结论: _________ (2)结论: _________ (3)结论: _________ (4)结论: _________
(2)的推理过程如下:
解:过点P作PQ∥AB
则∠1=∠A( _________ )
∵PQ∥AB(已作)且AB∥CD( _________ )
∴EF∥CD( _________ )
∴∠2=∠C( _________ )
∵∠APC=∠1+∠2
∴∠APC=∠C+∠B( _________ )
44.(2014?顺义区二模)【问题】:如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB.若∠A=80°,则∠BEC= _________ ;若∠A=n°,则∠BEC= _________ .
【探究】:
(1)如图2,在△ABC中,BD、BE三等分∠ABC,CD、CE三等分∠ACB.若∠A=n°,则∠BEC= _________ ;
(2)如图3,在△ABC中,BE平分∠ABC,CE平分外角∠ACM.若∠A=n°,则∠BEC= _________ ;
(3)如图4,在△ABC中,BE平分外角∠CBM,CE平分外角∠BCN.若∠A=n°,则∠BEC= _________ .
45.(2012?樊城区模拟)下面是有关三角形内外角平分线的探究,阅读后按要求作答:?
探究1:如图(1),在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现:∠BOC=90°+∠A(不要求证明).
探究2:如图(2)中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的数量关系?请说明理由.?
探究3:如图(3)中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的数量关系?(只写结论,不需证明).结论: _________ .?
1.如图,l1∥l2.若∠2=2∠1,则∠1=_______,∠2=_______.
2.小明不小心将形状是梯形的玻璃打碎成两部分(如图).若量得上半部分的∠A=123°,∠D=104°,则原梯形玻璃下半部分的∠B=_______,∠C=_______.
3.如图,用吸管吮吸易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹角∠2=_______ .
4.如图,AB∥CD,∠A=35°,∠C=78°,则∠M=_______.
5.如图,CD平分∠ACB,DE∥BC,∠AED=80°,则∠EDC=_______.
6.如图,AB∥CD,∠BAE=40°,∠ECD=62°,EF平分∠AEC,则∠AEF=_______.
7.若—个多边形的每个外角都是72°,则这个多边形是_______边形,它的内角和为_______.
8.如图,已知△ABC的∠ABC和∠ACB的外角平分线交于点D,∠A=40°,则∠D=_______.
9.三角形两边的长分别为1和8.若该三角形第三边长为偶数,则该三角形的周长为_______.
10.如图,AB∥CD,直线MN与AB、CD分别交于E、F,GE⊥MN,∠1=130°,则∠2的度数为_______.
11.如图,等边三角形ABC沿边AB的方向平移到△BDE的位置,则图中∠CBE=_______,连接CE后,线段CE与AD的关系是_______.
12.如图,AB∥CD,∠D=80°,∠CAD:∠BAC=3:2,则∠CAD=_______.
13.如图,把△ABC平移到△DEF的位置,若AB=5 cm,则DE=_______;如果∠A=65°,∠B=30°,那么∠F=_______.
14.如图,把△ABC沿RS的方向平移到△DEF的位置,则AB∥_______,BC=_______;如果∠A=80°,那么∠D=_______.
15.如图,已知DE∥AB,∠ACD=75°,∠B=25°,则∠ACB的度数为_______.
二、选择题(每题2分,共22分)
16.经过平移,图形上的每个点都沿同一方向移动
了一定距离,下列说法中正确的是 ( )
A.不同的点移动的距离不同 B.不同的点移动的距离相同
C.不同的点移动的距离可能相同,也可能不同 D.无法确定
17.已知在△ABC中有两个角的大小分别为40°和70°,则这个三角形是 ( )
A.直角三角形 B.等边三角形 C钝角三角形 D.等腰三角形
19.下列角平分线中互相垂直的是 ( )
A.对顶角的平分线 B.两条平行线被第三条直线所截,内错角的平分线
C.两条平行线被第三条直线所截,同位角的平分线 D.两条平行线被第三条直线所截,同旁内角的平分线
20.已知等腰三角形的一个底角是30°,则这个三角形的顶角等于 ( )
A.150° B.120° C.75° D.30°
21.下列说法:①钝角三角形有两条高在三角形内部;②三角形的三条高最多有两条不在三角形内部;③三角形的三条高的交点不在三角形内部,就在三角形外部;④钝角三角形三个内角的平分线的交点一定不在三角形内部.其中正确的个数为 ( )A.1个 B.2个 C.3个 D.4个
23.下列叙述错误的是 ( )
A.△ABC中,∠A +∠B<∠C,此三角形不一定为钝角三角形
B.三角形可分为锐角三角形、直角三角形和钝角三角形
C.若三角形的一个外角小于与它相邻的一个内角,则这个三角形为钝角三角形
D.直角三角形只有一条高在三角形内
24.等腰三角形的一边长等于5,另一边长等于9,它的周长是 ( )
A.19 B.14 C.23 D.19或23
25.如图,∠1=∠2,∠DAB=∠BCD.给出下列结论:①AB∥DC;②AD∥BC;③∠B=∠D;④∠D=∠DAC.其中,正确的结论有 ( )A.1个 B.2个 C.3个 D.4个
26.如图,∠1+23=90°,∠2-∠3=90°,∠4=115°,那么23的度数是 ( )
A.45° B.65° C.60° D.75°
29.(5分)如图,AD∥BC,∠A=96°,∠D=104°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.
30.(6分)如图,AB∥CD,∠1:∠2:∠3=1:2:3.
(1)求∠3的度数;
(2)∠EBA与∠2相等吗?为什么?
31.(6分)如图,把一张长方形纸片ABCD沿EF折叠,C点落在C'处,D点落在D'处,ED'交BC于点G.已知∠EFG= 50°,试求∠DEG与∠BGD'的度数.
32.(6分)如图,AD⊥BC,EG⊥BC,垂足分别为D、G,∠E=∠AFE.试说明AD是△ABC的角平分线.
33.(7分)如图,CE平分∠ACD,F为CA延长线上一点,FG∥CE交AB于点G,∠ACD=100°,∠AGF=20°,你能求出∠B的度数吗?若能,请写出求解过程;若不能,请说明理由.
34.(8分)如图,O是△ABC的3条角平分线的交点,OG⊥BC,垂足为G.
(1)猜想∠BOC与90°+∠BAC之间的数量关系,并说明理由;
(2)∠DOB与∠GOC相等吗?为什么?
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
