2017-2018学年华师大版九年级数学第一轮复习教案3几何图形的折叠与动点问题
文档属性
| 名称 | 2017-2018学年华师大版九年级数学第一轮复习教案3几何图形的折叠与动点问题 |

|
|
| 格式 | zip | ||
| 文件大小 | 238.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-05 00:00:00 | ||
图片预览


文档简介
2017-2018学年度 九 年级 班 数学 教案
课 题
几何图形的折叠与动点问题
课 型
新授课
节数
1
备课人
审核人
授课人
日期
教
学
目
标
知识与技能
几何图形的折叠与动点问题
过程与方法
让学生经历求几何图形的折叠与动点问题探索过程,理解几何图形的折叠与动点问题的求法
情感态度
进一步培养数形结合方法研究问题
教材
分析
重点
几何图形的折叠与动点问题
难点
几何图形的折叠与动点问题的相关计算
教学
模式
三疑三探
课时1
共____课时
学法
自学 合作 探究
主 案
副案(修改栏)
一、设疑自探(10分钟)
(一)创设情境,导入新课
我们学习了哪几种类型的几何图形的折叠与动点问题求法?它们又有哪些性质和联系?
(二)根据课题,提出问题。看到这个课题,你想知道什么?请提出来,预设:
自主学习,合作探究
多媒体展示(让学生先独立计算几何图形的折叠与动点问题,通过观察找出解法,然后同桌交流)
对照问题,总结规律
巩固练习
(积极参与探索图像之间的位置能否通过适当的变换得到,多和同学交流,并虚心采纳别人合理的意见)
出示自探提示,组织学生自探。( 分钟)自探提示:
自主学习:
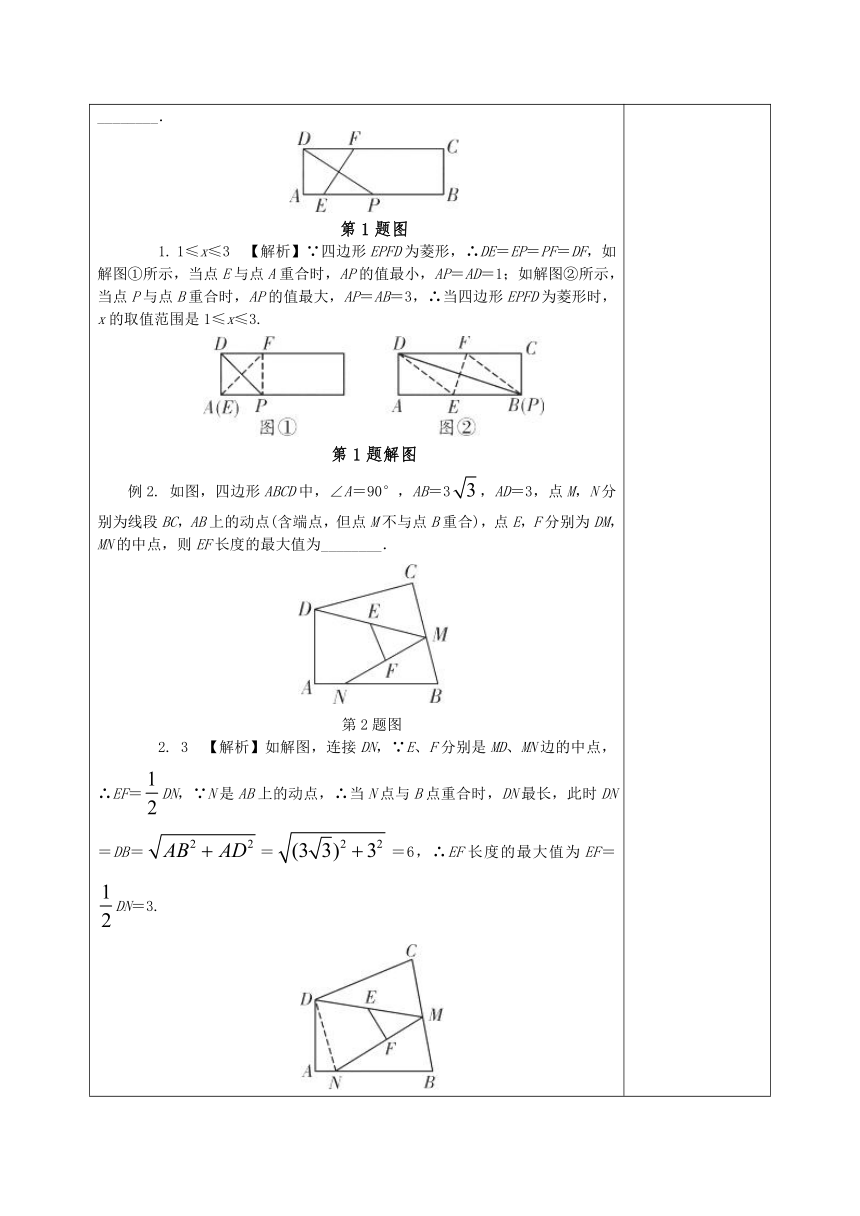
例1. 如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.那么使得四边形EPFD为菱形的x的取值范围是________.
第1题图
1. 1≤x≤3 【解析】∵四边形EPFD为菱形,∴DE=EP=PF=DF,如解图①所示,当点E与点A重合时,AP的值最小,AP=AD=1;如解图②所示,当点P与点B重合时,AP的值最大,AP=AB=3,∴当四边形EPFD为菱形时,x的取值范围是1≤x≤3.
第1题解图
例2. 如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为________.
第2题图
2. 3 【解析】如解图,连接DN,∵E、F分别是MD、MN边的中点,∴EF=DN,∵N是AB上的动点,∴当N点与B点重合时,DN最长,此时DN=DB===6,∴EF长度的最大值为EF=DN=3.
第2题解图
例3. 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C′处,连接C′D交AB于点E,连接BC′,当△BC′D是直角三角形时,DE的长为________.
第3题图
3. 或 【解析】如解图①所示:点E与点C′重合时,即∠DEB=90°时,在Rt△ABC中,BC==4,由翻折的性质可知:AE=AC=3,DC=DE,则EB=2,设CD=DE=x,则BD=4-x,在Rt△DBE中,DE2+BE2=DB2,即x2+22=(4-x)2.解得:x=,∴DE=.如解图②所示,∠EDB=90°时,由翻折的性质可知:AC=AC′,∠C=∠AC′D=90°,∵∠C=∠AC′D=∠CDC′=90°,∴四边形ACDC′为矩形,又∵AC=AC′,∴四边形ACDC′为正方形,∴CD=AC=3,∴DB=BC-DC=4-3=1.∵DE∥AC,∴△BDE∽△BCA,∴==,即=,解得:DE=.若∠DBC′=90°,则四边形ACBC′为矩形,AC≠BC,故C、C′折叠不可能重合.故∠DBC′不可能为直角,∴DE长为或.
第3题解图
二、解疑合探( 分钟)
(一).小组合探。
1.小组内讨论解决自探中未解决的问题;
2.教师出示展示与评价分工。
问题
1
2
3
展示
3
8
7
评价
4
5
6
(二).全班合探。
1.学生展示与评价;
2.教师点拨或精讲。
合作探究
(1) 请比较这三个例题有什么共同特征?
(2) 由此,你发现了什么?
在学生做题时,教师巡视指导
探究活动由学生自主探究后小组交流,对有困难的学生教师可适当点拨
教师演示多媒体
质疑再探:( 分钟)
1.现在,我们已经解决了自探问题。下面我们再回看一下,开始我们提出的问题还有那些没有解决?
问题已解决
2.本节的知识已经学完,对于本节的学习,谁还有什么问题或不明白的地方?请提出来,大家一起来解决.
四、运用拓展( 分钟)
(一)根据本节学习内容,学生自编习题,交流解答。
请你来当小老师,编一道题,考考大家(同桌)!
根据学生自编习题的练习情况,教师有选择地出示下面的习题共学生练习。为了巩固本节知识,加强知识的运用拓展,老师也给大家设计了一些习题,检测一下大家对本节知识的掌握与运用情况,请看:
1. 如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在边AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为________.
第1题图
2. 如图,在菱形ABCD中,∠A=60°,AD=3,点E为AB边上一个动点(不与端点重合),过A、E在菱形ABCD内部作菱形AEGF,交AD边于点F,连接BG、GC,当△GBC为等腰三角形时,AF的长为___2或3- _____.
第2题图
3. 如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D(不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为___2或2-2_____.
第3题图
(三)全课总结
1.学生谈学习收获。通过这节课的学习,你都有哪些收获?谈一谈.
2.学科班长评价本节课活动情况。
作业设计
资料习题
板书设计
作业布置
教 学反 思
课 题
几何图形的折叠与动点问题
课 型
新授课
节数
1
备课人
审核人
授课人
日期
教
学
目
标
知识与技能
几何图形的折叠与动点问题
过程与方法
让学生经历求几何图形的折叠与动点问题探索过程,理解几何图形的折叠与动点问题的求法
情感态度
进一步培养数形结合方法研究问题
教材
分析
重点
几何图形的折叠与动点问题
难点
几何图形的折叠与动点问题的相关计算
教学
模式
三疑三探
课时1
共____课时
学法
自学 合作 探究
主 案
副案(修改栏)
一、设疑自探(10分钟)
(一)创设情境,导入新课
我们学习了哪几种类型的几何图形的折叠与动点问题求法?它们又有哪些性质和联系?
(二)根据课题,提出问题。看到这个课题,你想知道什么?请提出来,预设:
自主学习,合作探究
多媒体展示(让学生先独立计算几何图形的折叠与动点问题,通过观察找出解法,然后同桌交流)
对照问题,总结规律
巩固练习
(积极参与探索图像之间的位置能否通过适当的变换得到,多和同学交流,并虚心采纳别人合理的意见)
出示自探提示,组织学生自探。( 分钟)自探提示:
自主学习:
例1. 如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=x,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.那么使得四边形EPFD为菱形的x的取值范围是________.
第1题图
1. 1≤x≤3 【解析】∵四边形EPFD为菱形,∴DE=EP=PF=DF,如解图①所示,当点E与点A重合时,AP的值最小,AP=AD=1;如解图②所示,当点P与点B重合时,AP的值最大,AP=AB=3,∴当四边形EPFD为菱形时,x的取值范围是1≤x≤3.
第1题解图
例2. 如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为________.
第2题图
2. 3 【解析】如解图,连接DN,∵E、F分别是MD、MN边的中点,∴EF=DN,∵N是AB上的动点,∴当N点与B点重合时,DN最长,此时DN=DB===6,∴EF长度的最大值为EF=DN=3.
第2题解图
例3. 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C′处,连接C′D交AB于点E,连接BC′,当△BC′D是直角三角形时,DE的长为________.
第3题图
3. 或 【解析】如解图①所示:点E与点C′重合时,即∠DEB=90°时,在Rt△ABC中,BC==4,由翻折的性质可知:AE=AC=3,DC=DE,则EB=2,设CD=DE=x,则BD=4-x,在Rt△DBE中,DE2+BE2=DB2,即x2+22=(4-x)2.解得:x=,∴DE=.如解图②所示,∠EDB=90°时,由翻折的性质可知:AC=AC′,∠C=∠AC′D=90°,∵∠C=∠AC′D=∠CDC′=90°,∴四边形ACDC′为矩形,又∵AC=AC′,∴四边形ACDC′为正方形,∴CD=AC=3,∴DB=BC-DC=4-3=1.∵DE∥AC,∴△BDE∽△BCA,∴==,即=,解得:DE=.若∠DBC′=90°,则四边形ACBC′为矩形,AC≠BC,故C、C′折叠不可能重合.故∠DBC′不可能为直角,∴DE长为或.
第3题解图
二、解疑合探( 分钟)
(一).小组合探。
1.小组内讨论解决自探中未解决的问题;
2.教师出示展示与评价分工。
问题
1
2
3
展示
3
8
7
评价
4
5
6
(二).全班合探。
1.学生展示与评价;
2.教师点拨或精讲。
合作探究
(1) 请比较这三个例题有什么共同特征?
(2) 由此,你发现了什么?
在学生做题时,教师巡视指导
探究活动由学生自主探究后小组交流,对有困难的学生教师可适当点拨
教师演示多媒体
质疑再探:( 分钟)
1.现在,我们已经解决了自探问题。下面我们再回看一下,开始我们提出的问题还有那些没有解决?
问题已解决
2.本节的知识已经学完,对于本节的学习,谁还有什么问题或不明白的地方?请提出来,大家一起来解决.
四、运用拓展( 分钟)
(一)根据本节学习内容,学生自编习题,交流解答。
请你来当小老师,编一道题,考考大家(同桌)!
根据学生自编习题的练习情况,教师有选择地出示下面的习题共学生练习。为了巩固本节知识,加强知识的运用拓展,老师也给大家设计了一些习题,检测一下大家对本节知识的掌握与运用情况,请看:
1. 如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在边AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为________.
第1题图
2. 如图,在菱形ABCD中,∠A=60°,AD=3,点E为AB边上一个动点(不与端点重合),过A、E在菱形ABCD内部作菱形AEGF,交AD边于点F,连接BG、GC,当△GBC为等腰三角形时,AF的长为___2或3- _____.
第2题图
3. 如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D(不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为___2或2-2_____.
第3题图
(三)全课总结
1.学生谈学习收获。通过这节课的学习,你都有哪些收获?谈一谈.
2.学科班长评价本节课活动情况。
作业设计
资料习题
板书设计
作业布置
教 学反 思
同课章节目录
