2017-2018学年华师大版九年级数学第一轮复习教案5、阴影部分面积的相关计算
文档属性
| 名称 | 2017-2018学年华师大版九年级数学第一轮复习教案5、阴影部分面积的相关计算 | 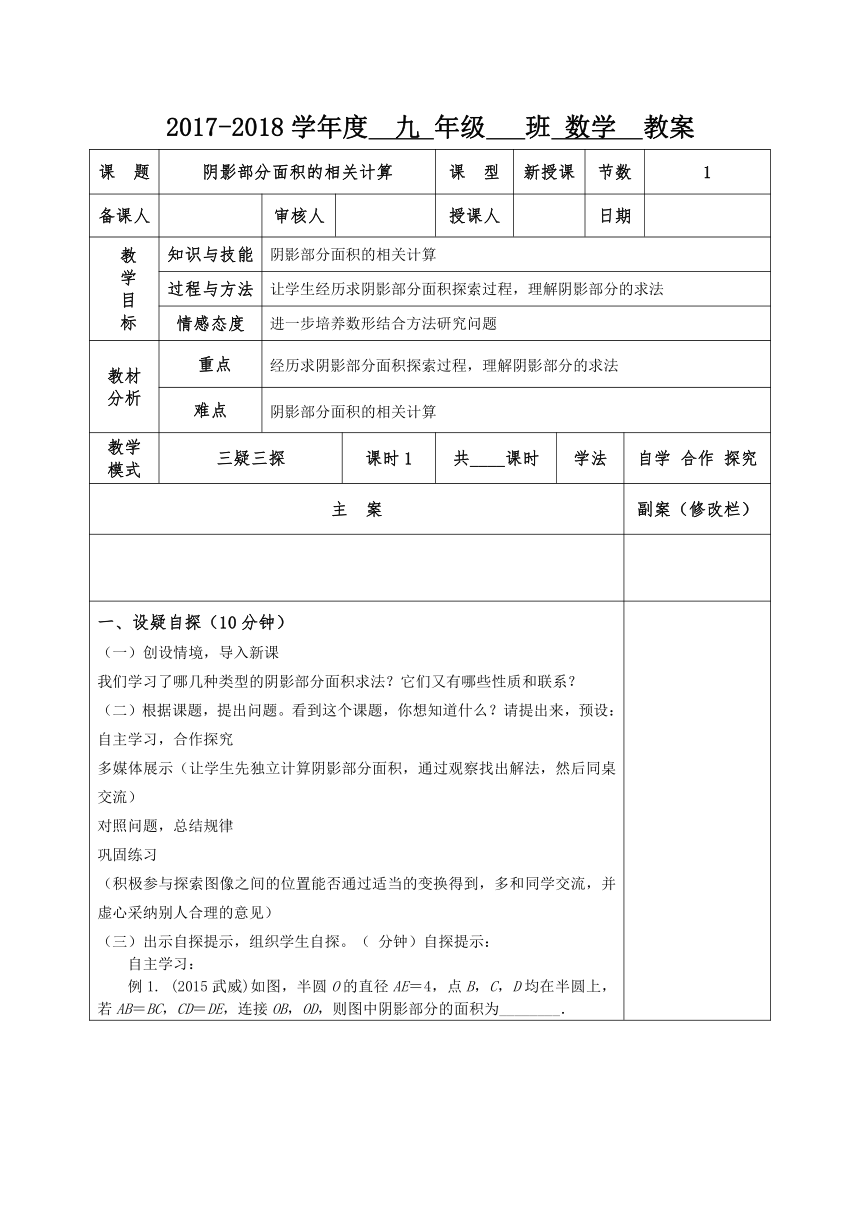 | |
| 格式 | zip | ||
| 文件大小 | 226.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-05 14:51:08 | ||
图片预览


文档简介
2017-2018学年度 九 年级 班 数学 教案
课 题
阴影部分面积的相关计算
课 型
新授课
节数
1
备课人
审核人
授课人
日期
教
学
目
标
知识与技能
阴影部分面积的相关计算
过程与方法
让学生经历求阴影部分面积探索过程,理解阴影部分的求法
情感态度
进一步培养数形结合方法研究问题
教材
分析
重点
经历求阴影部分面积探索过程,理解阴影部分的求法
难点
阴影部分面积的相关计算
教学
模式
三疑三探
课时1
共____课时
学法
自学 合作 探究
主 案
副案(修改栏)
一、设疑自探(10分钟)
(一)创设情境,导入新课
我们学习了哪几种类型的阴影部分面积求法?它们又有哪些性质和联系?
(二)根据课题,提出问题。看到这个课题,你想知道什么?请提出来,预设:
自主学习,合作探究
多媒体展示(让学生先独立计算阴影部分面积,通过观察找出解法,然后同桌交流)
对照问题,总结规律
巩固练习
(积极参与探索图像之间的位置能否通过适当的变换得到,多和同学交流,并虚心采纳别人合理的意见)
出示自探提示,组织学生自探。( 分钟)自探提示:
自主学习:
例1. (2015武威)如图,半圆O的直径AE=4,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为________.
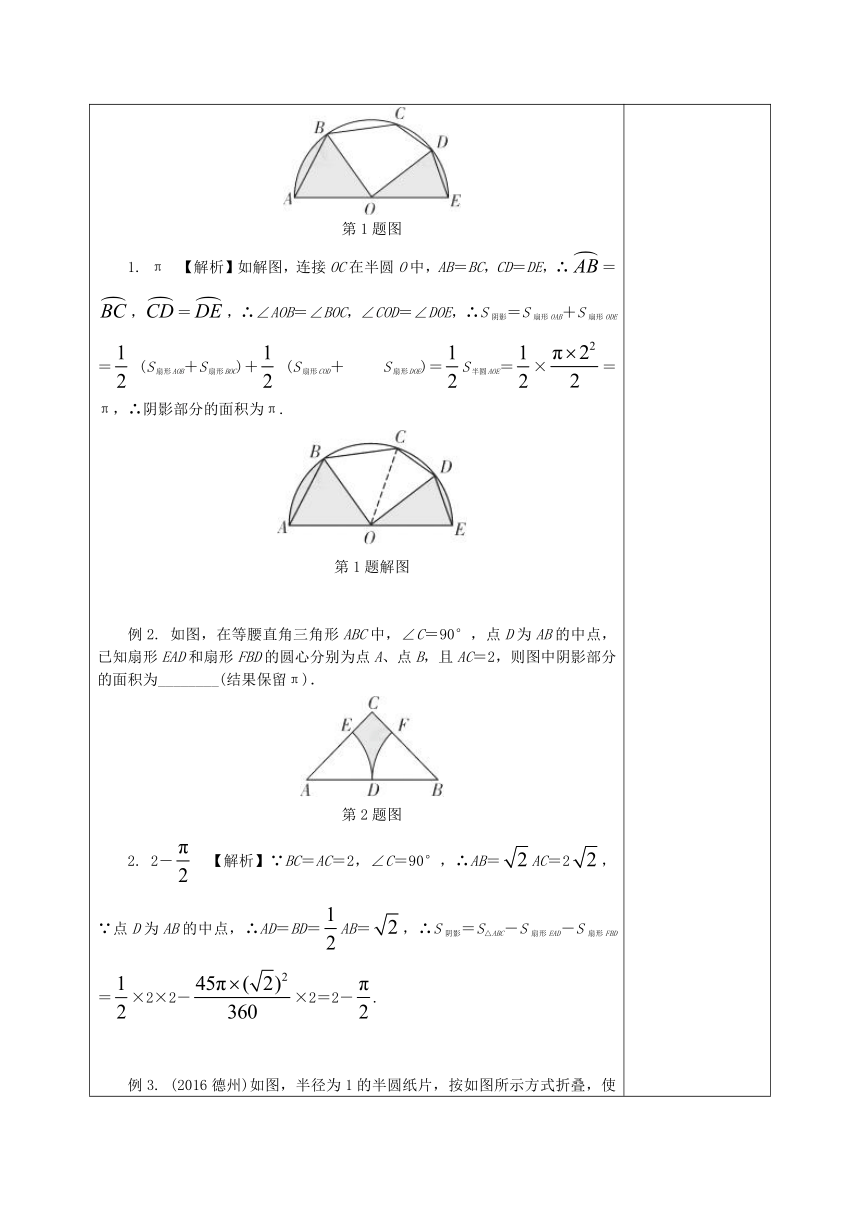
第1题图
1. π 【解析】如解图,连接OC在半圆O中,AB=BC,CD=DE,∴=,=,∴∠AOB=∠BOC,∠COD=∠DOE,∴S阴影=S扇形OAB+S扇形ODE= (S扇形AOB+S扇形BOC)+ (S扇形COD+ S扇形DOE)=S半圆AOE=×=π,∴阴影部分的面积为π.
第1题解图
例2. 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AC=2,则图中阴影部分的面积为________(结果保留π).
第2题图
2. 2- 【解析】∵BC=AC=2,∠C=90°,∴AB=AC=2,∵点D为AB的中点,∴AD=BD=AB=,∴S阴影=S△ABC-S扇形EAD-S扇形FBD=×2×2-×2=2-.
例3. (2016德州)如图,半径为1的半圆纸片,按如图所示方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是________.
第13题图
3. - 【解析】如解图,连接OM交AB于点C,连接OA、OB,根据题意OM⊥AB且OC=MC=,在Rt△AOC中,∵OA=1,OC=,∴cos∠AOC==,AC==,∴∠AOC=60°,AB=2AC=,∴∠AOB=2∠AOC=120°,则S弓形ABM=
S扇形OAB-S△AOB=-××=-,S阴影=S半圆-2
S弓形ABM=π×12-2(-)=-.
第3题解图
二、解疑合探( 分钟)
(一).小组合探。
1.小组内讨论解决自探中未解决的问题;
2.教师出示展示与评价分工。
问题
1
2
3
展示
1
2
3
评价
4
5
6
(二).全班合探。
1.学生展示与评价;
2.教师点拨或精讲。
合作探究
(1) 请比较这三个例题有什么共同特征?
(2) 由此,你发现了什么?
在学生做题时,教师巡视指导
探究活动由学生自主探究后小组交流,对有困难的学生教师可适当点拨
教师演示多媒体
质疑再探:( 分钟)
1.现在,我们已经解决了自探问题。下面我们再回看一下,开始我们提出的问题还有那些没有解决?
问题已解决
2.本节的知识已经学完,对于本节的学习,谁还有什么问题或不明白的地方?请提出来,大家一起来解决.
四、运用拓展( 分钟)
(一)根据本节学习内容,学生自编习题,交流解答。
请你来当小老师,编一道题,考考大家(同桌)!
根据学生自编习题的练习情况,教师有选择地出示下面的习题共学生练习。为了巩固本节知识,加强知识的运用拓展,老师也给大家设计了一些习题,检测一下大家对本节知识的掌握与运用情况,请看:
1. 如图,平行四边形ABCD中,BE⊥AD于点E,以C为圆心,BC长为半径画弧,恰好过AD的中点F,若BC=4,BE=2,则图中阴影部分的面积为________.
第6题图
2. 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是________.
第7题图
3. 如图,在以O为圆心、4 cm为半径的扇形AOB中,∠AOB=90°,再分别以OA、OB为直径在扇形AOB内作半圆,则图中阴影部分的面积为________.
第8题图
(三)全课总结
1.学生谈学习收获。通过这节课的学习,你都有哪些收获?谈一谈.
2.学科班长评价本节课活动情况。
作业设计
资料习题
板书设计
1、
2、
作业布置
教 学反 思
课 题
阴影部分面积的相关计算
课 型
新授课
节数
1
备课人
审核人
授课人
日期
教
学
目
标
知识与技能
阴影部分面积的相关计算
过程与方法
让学生经历求阴影部分面积探索过程,理解阴影部分的求法
情感态度
进一步培养数形结合方法研究问题
教材
分析
重点
经历求阴影部分面积探索过程,理解阴影部分的求法
难点
阴影部分面积的相关计算
教学
模式
三疑三探
课时1
共____课时
学法
自学 合作 探究
主 案
副案(修改栏)
一、设疑自探(10分钟)
(一)创设情境,导入新课
我们学习了哪几种类型的阴影部分面积求法?它们又有哪些性质和联系?
(二)根据课题,提出问题。看到这个课题,你想知道什么?请提出来,预设:
自主学习,合作探究
多媒体展示(让学生先独立计算阴影部分面积,通过观察找出解法,然后同桌交流)
对照问题,总结规律
巩固练习
(积极参与探索图像之间的位置能否通过适当的变换得到,多和同学交流,并虚心采纳别人合理的意见)
出示自探提示,组织学生自探。( 分钟)自探提示:
自主学习:
例1. (2015武威)如图,半圆O的直径AE=4,点B,C,D均在半圆上,若AB=BC,CD=DE,连接OB,OD,则图中阴影部分的面积为________.
第1题图
1. π 【解析】如解图,连接OC在半圆O中,AB=BC,CD=DE,∴=,=,∴∠AOB=∠BOC,∠COD=∠DOE,∴S阴影=S扇形OAB+S扇形ODE= (S扇形AOB+S扇形BOC)+ (S扇形COD+ S扇形DOE)=S半圆AOE=×=π,∴阴影部分的面积为π.
第1题解图
例2. 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AC=2,则图中阴影部分的面积为________(结果保留π).
第2题图
2. 2- 【解析】∵BC=AC=2,∠C=90°,∴AB=AC=2,∵点D为AB的中点,∴AD=BD=AB=,∴S阴影=S△ABC-S扇形EAD-S扇形FBD=×2×2-×2=2-.
例3. (2016德州)如图,半径为1的半圆纸片,按如图所示方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是________.
第13题图
3. - 【解析】如解图,连接OM交AB于点C,连接OA、OB,根据题意OM⊥AB且OC=MC=,在Rt△AOC中,∵OA=1,OC=,∴cos∠AOC==,AC==,∴∠AOC=60°,AB=2AC=,∴∠AOB=2∠AOC=120°,则S弓形ABM=
S扇形OAB-S△AOB=-××=-,S阴影=S半圆-2
S弓形ABM=π×12-2(-)=-.
第3题解图
二、解疑合探( 分钟)
(一).小组合探。
1.小组内讨论解决自探中未解决的问题;
2.教师出示展示与评价分工。
问题
1
2
3
展示
1
2
3
评价
4
5
6
(二).全班合探。
1.学生展示与评价;
2.教师点拨或精讲。
合作探究
(1) 请比较这三个例题有什么共同特征?
(2) 由此,你发现了什么?
在学生做题时,教师巡视指导
探究活动由学生自主探究后小组交流,对有困难的学生教师可适当点拨
教师演示多媒体
质疑再探:( 分钟)
1.现在,我们已经解决了自探问题。下面我们再回看一下,开始我们提出的问题还有那些没有解决?
问题已解决
2.本节的知识已经学完,对于本节的学习,谁还有什么问题或不明白的地方?请提出来,大家一起来解决.
四、运用拓展( 分钟)
(一)根据本节学习内容,学生自编习题,交流解答。
请你来当小老师,编一道题,考考大家(同桌)!
根据学生自编习题的练习情况,教师有选择地出示下面的习题共学生练习。为了巩固本节知识,加强知识的运用拓展,老师也给大家设计了一些习题,检测一下大家对本节知识的掌握与运用情况,请看:
1. 如图,平行四边形ABCD中,BE⊥AD于点E,以C为圆心,BC长为半径画弧,恰好过AD的中点F,若BC=4,BE=2,则图中阴影部分的面积为________.
第6题图
2. 如图,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是________.
第7题图
3. 如图,在以O为圆心、4 cm为半径的扇形AOB中,∠AOB=90°,再分别以OA、OB为直径在扇形AOB内作半圆,则图中阴影部分的面积为________.
第8题图
(三)全课总结
1.学生谈学习收获。通过这节课的学习,你都有哪些收获?谈一谈.
2.学科班长评价本节课活动情况。
作业设计
资料习题
板书设计
1、
2、
作业布置
教 学反 思
同课章节目录
