2018年北师大七年级下第五章生活中的轴对称单元测试含答案
文档属性
| 名称 | 2018年北师大七年级下第五章生活中的轴对称单元测试含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 195.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-05 00:00:00 | ||
图片预览

文档简介
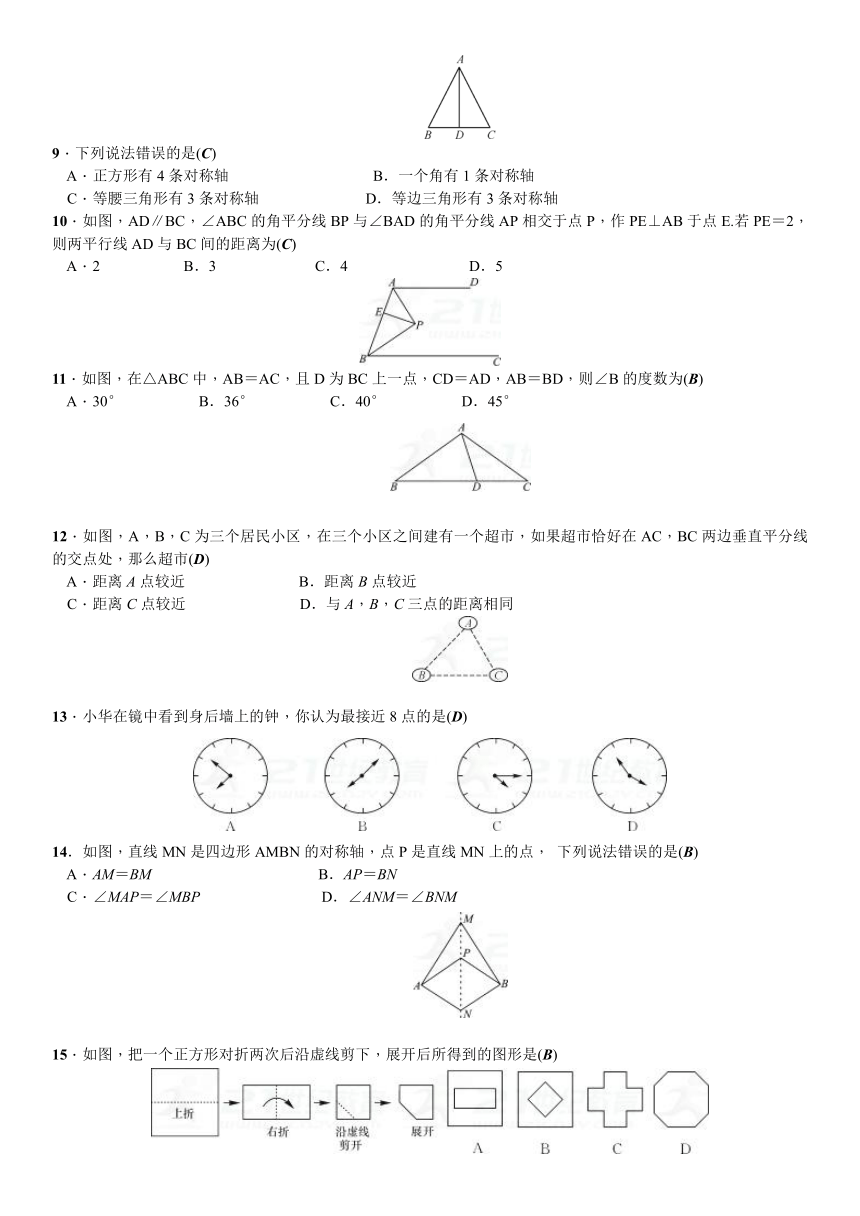
单元测试(五) 生活中的轴对称(BJ)
(时间:120分钟 满分:150分)
一、选择题(本大题共15小题,每小题3分,共45分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案
C
B
C
B
B
B
A
D
C
C
B
D
D
B
B
1.下面有4个汽车标志图案,其中是轴对称图形的有(C)
A.1个 B.2个 C.3个 D.4个
2.下列英文字母中,经轴对称变换后形状不发生变化的是(B)
A.AHIOTXZ B.HIOX
C.AHIOTNSQUVXC D.都不变形状
3.如图,正方形地砖的图案是轴对称图形,该图形的对称轴有(C)
A.1条 B.2条 C.4条 D.8条
4.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为(B)
A.6 B.5 C.4 D.3
5.等腰三角形的顶角为80°,则它的底角是(B)
A.20° B.50° C.60° D.80°
6.点P与点P1关于直线l成轴对称,则PP1与直线l的位置关系是(B)
A.平行 B.垂直
C.平行或垂直 D.不确定
7.下图的尺规作图是作(A)
A.线段的垂直平分线 B.一个半径定值的圆
C.一条直线的平行线 D.一个角等于已知角
8.如图,△ABC中,AB=AC,AD是中线,则下列结论中不一定正确的是(D)
A.∠B=∠C B.∠BAD=∠DAC
C.∠ADB=∠ADC D.∠BAC=∠C
9.下列说法错误的是(C)
A.正方形有4条对称轴 B.一个角有1条对称轴
C.等腰三角形有3条对称轴 D.等边三角形有3条对称轴
10.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为(C)
A.2 B.3 C.4 D.5
11.如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为(B)
A.30° B.36° C.40° D.45°
12.如图,A,B,C为三个居民小区,在三个小区之间建有一个超市,如果超市恰好在AC,BC两边垂直平分线的交点处,那么超市(D)
A.距离A点较近 B.距离B点较近
C.距离C点较近 D.与A,B,C三点的距离相同
13.小华在镜中看到身后墙上的钟,你认为最接近8点的是(D)
14.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点, 下列说法错误的是(B)
A.AM=BM B.AP=BN
C.∠MAP=∠MBP D.∠ANM=∠BNM
15.如图,把一个正方形对折两次后沿虚线剪下,展开后所得到的图形是(B)
二、填空题(本大题共5小题,每小题5分,共25分)
16.26个英文字母中,有很多都具有轴对称结构,请你写出其中具有轴对称结构的字母(至少3个)答案不唯一,如A,B,C.
17.如图所示,两个三角形关于某直线成轴对称,已知某些边的边长和某些角的度数,则α=60°,y=4__cm.
18.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,若∠BAC=70°,则∠BAD=35°.
19.如图,正方形的边长为3 cm,则图中阴影部分的面积为4.5cm2.
20.如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于2∶3∶4.
三、解答题(本大题共7小题,共80分)
21.(8分)(抚州中考)如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
解:如图所示.
22.(8分)下列三个图形,均由4个完全相同的小正方形组合而成,分别添加一个相同的正方形,使它们成为不同的轴对称图形.
解:如图所示.
23.(10分)电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定了(AB=AC),但有工作人员认为看上去有点倾斜,请你帮助工作人员测一下电线杆是否倾斜,并说明理由.
解:测量BD与DC,若BD=DC,说明D为BC中点,那么AD为△ABC中线.
又因为△ABC是等腰三角形,所以AD是△ABC的高线,所以AD⊥BC所以电线杆不倾斜.
24.(12分)如图,在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)若网格上的最小正方形的边长为1,求△ABC的面积.
解:(1)如图所示.
(2)此三角形面积为S△ABC=2×3-2×(×1×2)-×1×3=6-2-=.
25.(12分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A,B为垂足,AB交OM于点N,试说明:∠OAB=∠OBA.
解:因为OM平分∠POQ,MA⊥OP,MB⊥OQ,
所以MA=MB.所以△AMB是等腰三角形.
所以∠MAB=∠MBA.
又因为∠MAO=∠MBO=90 °,
所以∠MAO-∠MAB=∠MBO-∠MBA.
即∠OAB=∠OBA.
26.(14分)如图,EFGH是正方形弹子球台面,有黑白两球分别位于A、B两点的位置上,试问怎样撞击黑球A,才能使黑球A碰撞台边EF反弹后能击中白球B?
解:如图.
(1)作点A关于EF的对称点A′;
(2)连接A′B,交EF于点C;
(3)沿AC方向撞击黑球A,才能使黑球A碰撞台边EF反弹后能击中白球B.
27.(16分)(龙岩中考)如图,E,F分别是等边△ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.
(1)试说明:CE=BF;
(2)求∠BPC的度数.
解:(1)因为△ABC是等边三角形,所以BC=AB,∠A=∠EBC=60°.
在△BCE与△ABF中,
所以△BCE≌△ABF(SAS).所以CE=BF.
(2)因为△BCE≌△ABF,所以∠BCE=∠ABF.
所以∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60 °.
所以∠BPC=180 °-60 °=120 °.
(时间:120分钟 满分:150分)
一、选择题(本大题共15小题,每小题3分,共45分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案
C
B
C
B
B
B
A
D
C
C
B
D
D
B
B
1.下面有4个汽车标志图案,其中是轴对称图形的有(C)
A.1个 B.2个 C.3个 D.4个
2.下列英文字母中,经轴对称变换后形状不发生变化的是(B)
A.AHIOTXZ B.HIOX
C.AHIOTNSQUVXC D.都不变形状
3.如图,正方形地砖的图案是轴对称图形,该图形的对称轴有(C)
A.1条 B.2条 C.4条 D.8条
4.如图,直线CD是线段AB的垂直平分线,P为直线CD上的一点,已知线段PA=5,则线段PB的长度为(B)
A.6 B.5 C.4 D.3
5.等腰三角形的顶角为80°,则它的底角是(B)
A.20° B.50° C.60° D.80°
6.点P与点P1关于直线l成轴对称,则PP1与直线l的位置关系是(B)
A.平行 B.垂直
C.平行或垂直 D.不确定
7.下图的尺规作图是作(A)
A.线段的垂直平分线 B.一个半径定值的圆
C.一条直线的平行线 D.一个角等于已知角
8.如图,△ABC中,AB=AC,AD是中线,则下列结论中不一定正确的是(D)
A.∠B=∠C B.∠BAD=∠DAC
C.∠ADB=∠ADC D.∠BAC=∠C
9.下列说法错误的是(C)
A.正方形有4条对称轴 B.一个角有1条对称轴
C.等腰三角形有3条对称轴 D.等边三角形有3条对称轴
10.如图,AD∥BC,∠ABC的角平分线BP与∠BAD的角平分线AP相交于点P,作PE⊥AB于点E.若PE=2,则两平行线AD与BC间的距离为(C)
A.2 B.3 C.4 D.5
11.如图,在△ABC中,AB=AC,且D为BC上一点,CD=AD,AB=BD,则∠B的度数为(B)
A.30° B.36° C.40° D.45°
12.如图,A,B,C为三个居民小区,在三个小区之间建有一个超市,如果超市恰好在AC,BC两边垂直平分线的交点处,那么超市(D)
A.距离A点较近 B.距离B点较近
C.距离C点较近 D.与A,B,C三点的距离相同
13.小华在镜中看到身后墙上的钟,你认为最接近8点的是(D)
14.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点, 下列说法错误的是(B)
A.AM=BM B.AP=BN
C.∠MAP=∠MBP D.∠ANM=∠BNM
15.如图,把一个正方形对折两次后沿虚线剪下,展开后所得到的图形是(B)
二、填空题(本大题共5小题,每小题5分,共25分)
16.26个英文字母中,有很多都具有轴对称结构,请你写出其中具有轴对称结构的字母(至少3个)答案不唯一,如A,B,C.
17.如图所示,两个三角形关于某直线成轴对称,已知某些边的边长和某些角的度数,则α=60°,y=4__cm.
18.如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,若∠BAC=70°,则∠BAD=35°.
19.如图,正方形的边长为3 cm,则图中阴影部分的面积为4.5cm2.
20.如图,△ABC的三边AB,BC,CA的长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO∶S△BCO∶S△CAO等于2∶3∶4.
三、解答题(本大题共7小题,共80分)
21.(8分)(抚州中考)如图,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
解:如图所示.
22.(8分)下列三个图形,均由4个完全相同的小正方形组合而成,分别添加一个相同的正方形,使它们成为不同的轴对称图形.
解:如图所示.
23.(10分)电力工作人员栽完电线杆后,用两根等长的拉线把电线杆固定了(AB=AC),但有工作人员认为看上去有点倾斜,请你帮助工作人员测一下电线杆是否倾斜,并说明理由.
解:测量BD与DC,若BD=DC,说明D为BC中点,那么AD为△ABC中线.
又因为△ABC是等腰三角形,所以AD是△ABC的高线,所以AD⊥BC所以电线杆不倾斜.
24.(12分)如图,在正方形网格上有一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)若网格上的最小正方形的边长为1,求△ABC的面积.
解:(1)如图所示.
(2)此三角形面积为S△ABC=2×3-2×(×1×2)-×1×3=6-2-=.
25.(12分)如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,A,B为垂足,AB交OM于点N,试说明:∠OAB=∠OBA.
解:因为OM平分∠POQ,MA⊥OP,MB⊥OQ,
所以MA=MB.所以△AMB是等腰三角形.
所以∠MAB=∠MBA.
又因为∠MAO=∠MBO=90 °,
所以∠MAO-∠MAB=∠MBO-∠MBA.
即∠OAB=∠OBA.
26.(14分)如图,EFGH是正方形弹子球台面,有黑白两球分别位于A、B两点的位置上,试问怎样撞击黑球A,才能使黑球A碰撞台边EF反弹后能击中白球B?
解:如图.
(1)作点A关于EF的对称点A′;
(2)连接A′B,交EF于点C;
(3)沿AC方向撞击黑球A,才能使黑球A碰撞台边EF反弹后能击中白球B.
27.(16分)(龙岩中考)如图,E,F分别是等边△ABC的边AB,AC上的点,且BE=AF,CE,BF交于点P.
(1)试说明:CE=BF;
(2)求∠BPC的度数.
解:(1)因为△ABC是等边三角形,所以BC=AB,∠A=∠EBC=60°.
在△BCE与△ABF中,
所以△BCE≌△ABF(SAS).所以CE=BF.
(2)因为△BCE≌△ABF,所以∠BCE=∠ABF.
所以∠PBC+∠PCB=∠PBC+∠ABF=∠ABC=60 °.
所以∠BPC=180 °-60 °=120 °.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
