3.2 用关系式表示的变量间关系同步练习
文档属性
| 名称 | 3.2 用关系式表示的变量间关系同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 401.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-06 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
3.2 用关系式表示的变量间关系同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.用数学式子表示变量之间的关系的方法叫做关系式法,关系式法是表示变量关系的另一种方法.
2.用关系式表示自变量与因变量之间的关系,在现实生活中有着广泛地应用,同时也是以后学习函数的基础,应注意将因变量写在等式的左边,自变量写在等式的右边.
3. 在用关系式表示变量之间的关系时,要注明自变量的取值范围
①当表达式的分母不含有自变量时,自变量取全体实数.
②当表达式的分母中含有自变量时,自变量取值要使分母不为零.
③对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
基础知识和能力拓展精练
一、选择题
1.已知圆柱的高为3 cm,当圆柱的底面半径r(cm)由小变大时,圆柱的体积V(cm3)随之变化,则V与r的关系式是( )
A. V=πr2 B. V=3πr2 C. V=πr2 D. V=9πr2
2.汽车离开甲站10千米后,以60千米/时的速度匀速前进了小时,则汽车离开甲站所走的路程(千米)与时间(小时)之间的关系式是( )
A. B. C. D.
3.已知齿轮每分钟转 EMBED Equation.DSMT4 转,如果用(转)表示转数, (分)表示转动的时间,那么用表示的关系式为( ).
A. B. C. D.
4.如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为( )
A. y=10x B. y=25x C. y=x D. y=x
5.李大爷要围成一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的长方形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的关系式是( )
A. y=-2x+24(0<x<12) B. y=-x+12(0<x<24)
C. y=2x-24(0<x<12) D. y=x-12(0<x<24)
6.某大剧场地面的一部分为扇形,观众席的座位数按下列方式设置:
排数(x) 1 2 3 4 …
座位数(y) 50 53 56 59 …
有下列结论:①排数x是自变量,座位数y是因变量;②排数x是因变量,座位数y是自变量;③y=50+3x;④y=47+3x,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
7.如图,梯形上底长、下底长分别是x,y,高是6,面积是24,则y与x之间的表达式是( )
A. y=﹣x+8 B. y=﹣x+4 C. y=x﹣8 D. y=x﹣4
8.油箱中存油,油从油箱中均匀流出,流速为,则油箱中剩余油量与流出时间的关系式是( ).
A. B. C. D.
9.一个长方形的周长为30,则长方形的面积y与长方形一边长x的关系式为( )
A. y=x(15-x) B. y=x(30-x) C. y=x(30-2x) D. y=x(15+x)
10.某种签字笔的单价为2元,购买这种签字笔x支的总价为y元,则y与x之间的函数关系式为( )
A. y=- EMBED Equation.DSMT4 x B. y=x C. y=-2x D. y=2x
二、填空题
11.宁宁同学设计了一个计算程序如下表:
输入数据 1 2 3 4 5 …
输出数据 …
根据表格中的数据的对应关系,可得出输出数据y与输入数据x之间的关系式为___________.
12.某种储蓄的月利率是0.2%,存入100元本金后,不扣除利息税,本息和y(元)与所存月数x(x为正整数)之间的关系为__________,4个月的本息和为________.
13.李老师带领x名学生到某动物园参观,已知成人票每张20元,学生票每张10元.设门票的总费用为y元,则y=________.
14.若一个长方体底面积为60cm2,高为hcm,则体积V(cm3)与h(cm)的关系式为_____,若h从1cm变化到10cm时,长方体的体积由___cm3变化到___cm3.
15.小雨画了一个边长为3 cm的正方形,如果将正方形的边长增加x cm,那么面积的增加值y(cm2)与边长的增加值x(cm)之间的关系式为____________.
16.如图所示,梯形的上底长是厘米,下底长是厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.
()在这个变化过程中,自变量是__________,因变量是__________.
()梯形的面积与高(厘米)之间的关系式为__________.
()当梯形的高由厘米变化到厘米时,梯形的面积由__________变化到__________.
三、解答题
17.某地区现有果树24000棵,计划今后每年栽果树3000棵.
①试用含年数x(年)的式子表示果树总棵数y(棵);
②预计到第5年该地区有多少棵果树?
18.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h) 0 1 2 3 …
油箱剩余油量Q(L) 100 94 88 82 …
①根据上表的数据,请你写出Q与t的关系式;
②汽车行驶5h后,油箱中的剩余油量是多少?
③该品牌汽车的油箱加满50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
19.秋天到来了,小明家的苹果获得了丰收,他主动帮助妈妈到集市上去卖刚刚采摘下的苹果.已知销售数量x(千克)与售价y(元)的关系如下表所示:
数量x(千克) 1 2 3 4 5
售价y(元) 2.1 4.2 6.3 8.4 10.5
①根据表格中的数据,售价y是怎样随销售量的变化而变化的?
②求当x=15时,y的值是多少?
20.如图,一个半径为18 cm的圆,从中心挖去一个正方形,当挖去的正方形的边长由小变大时,剩下部分的面积也随之发生变化.
(1)若挖去的正方形边长为x(cm),剩下部分的面积为y(cm2),则y与x之间的关系式是什么
(2)当挖去的正方形的边长由1 cm变化到9 cm时,剩下部分的面积由____变化到____.
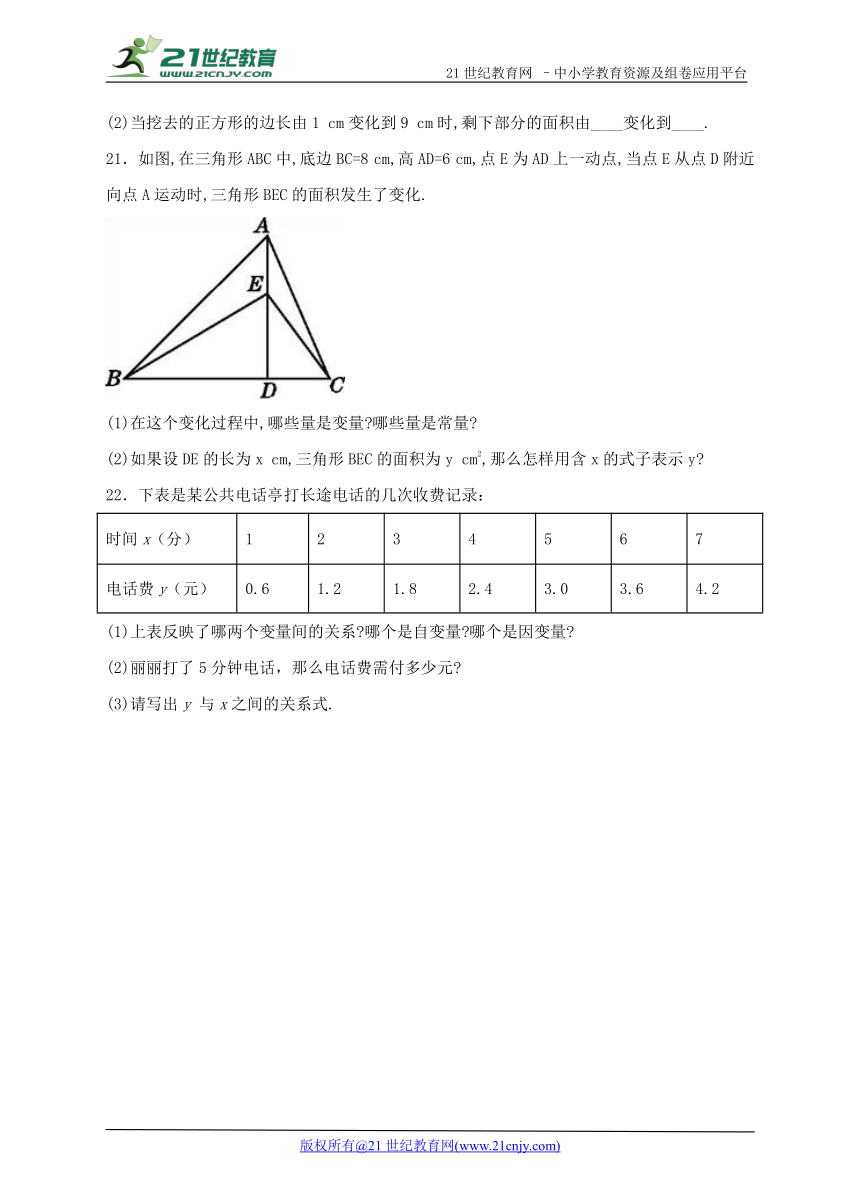
21.如图,在三角形ABC中,底边BC=8 cm,高AD=6 cm,点E为AD上一动点,当点E从点D附近向点A运动时,三角形BEC的面积发生了变化.
(1)在这个变化过程中,哪些量是变量 哪些量是常量
(2)如果设DE的长为x cm,三角形BEC的面积为y cm2,那么怎样用含x的式子表示y
22.下表是某公共电话亭打长途电话的几次收费记录:
时间x(分) 1 2 3 4 5 6 7
电话费y(元) 0.6 1.2 1.8 2.4 3.0 3.6 4.2
(1)上表反映了哪两个变量间的关系 哪个是自变量 哪个是因变量
(2)丽丽打了5分钟电话,那么电话费需付多少元
(3)请写出y 与x之间的关系式.
参考答案
1.B
【解析】∵圆柱的体积=底面积×高,该圆柱高为3cm,底面半径为cm,体积为cm3,
∴.
故选B.
2.A
【解析】根据路程与时间的关系,可得函数解析式:s=10+60t,
故选:A.
3.D
【解析】t表示转动的时间,那么在t分钟内齿轮转动的转数为:100t
即n=100t.
故选D.
4.D
【解析】解:25÷10=,所以购买钢笔的总钱数y(元)与支数x之间的关系式为:y=x.故选D.
点睛:此题主要考查了函数关系式的求法,以及单价、数量、总价的关系,要熟练掌握;解答此题的关键是根据单价=总价÷数量,求出每支钢笔的价格是多少.
5.B
【解析】由题意得:2y+x=24,
故可得:y= x+12(0故选:B.
6.B
【解析】根据图表可知随着排数的增大,座位数也增大.所以排数x是自变量,座位数y是因变量;
根据图标中的数据可得y=47+3x.故①④正确.
则选:B.
7.A
【解析】梯形上底长、下底长分别是x,y,高是6,面积是24,
则y与x之间的表达式是:24=(x+y)×6÷2,
即y=﹣x+8,
故选:A.
8.B
【解析】利用油箱中存油量20升-流出油量=剩余油量, 可得:流出油量是0.2t,
则剩余油量:Q=20 0.2t,故选:B.
9.A
【解析】∵长方形的周长为30,其中一边长为,
∴该长方形的另一边长为: ,
∴该长方形的面积: .
故选A.
10.D
【解析】依题意有:y=2x,
故选D.
11.y=
【解析】解:根据题意,得: .故答案为: .
12. y=100+0.2x 100.8元
【解析】第一个月y=100+100×0.2℅,
第二个月y=100+100×0.2℅+〔100+100×0.2℅〕×0.2℅
结合题干可知y=100(1+0.2℅x )= y=100+0.2x,
令x=4,求得y=100.8.
故答案为: y=100+0.2x;100.8元.
点睛:此题主要考查了函数解析式,根据题意,找到所求量的等量关系是解决问题的关键.
13.10x+20
【解析】根据总费用=成人票用钱数+学生票用钱数,可得y=10x+20.
故答案为:10x+20.
14. V=60h 60 600
【解析】根据长方体的体积=底面积×高,得:V=60h;
当h=1时,V=60,当h=10时,V=600,故长方体的体积由60 cm3变化到600 cm3.
故答案为:V=60h;60;600
15.y=x2+6x
【解析】由题意得y=(3+x)(3+x)-3×3=x +6x.
故答案为:y=x +6x.
16. 梯形的高 梯形的面积 90 9
【解析】(1)自变量是梯形的高,因变量是梯形的面积;
(2)梯形的面积y(cm )与高x(cm)之间的关系式为:y=(5+13)x×=9x;
(3)当梯形的高是l0cm时,y=9×10=90,
当梯形的高是l0cm时,y=9×1=9,
梯形的面积由90cm 变化到9cm .故答案为:梯形的高, 梯形的面积, y=9x, 90, 9.
17.①y=24000+3000x(x≥0,且x为正整数);②预计到第5年该地区有39000棵果树.
【解析】试题分析:①本题的等量关系是:果树的总数=现有的果树的数量+每年栽树的数量×年数,由此可得出关于果树总数与年数的函数关系式;
②根据①即可求出第5年的果树的数量.
试题解析:①根据题意得:y=24000+3000x(x≥0,且x为正整数);
②根据题意得:y=24000+3000x(x≥0,且x为正整数);
当x=5时,y=24000+3000×5=39000.
答:预计到第5年该地区有39000棵果树.
点睛:本题考查了根据实际问题列函数关系式,解题的关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出函数式,然后利用函数关系式即可解决题目的问题.
18.①Q=50﹣8t;②汽车行驶5h后,油箱中的剩余油量是10L;③该车最多能行驶625km.
【解析】试题分析:①由表格可知,开始油箱中的油为50L,每行驶1小时,油量减少8L,据此可得t与Q的关系式;
②求汽车行驶5h后,油箱中的剩余油量即是求当t=5时,Q的值;
③贮满50L汽油的汽车,理论上最多能行驶几小时即是求当Q=0时,t的值.
试题解析①Q与t的关系式为:Q=50﹣8t;
②当t=5时,Q=50﹣8×5=10,
答:汽车行驶5h后,油箱中的剩余油量是10L;
③当Q=0时,0=50﹣8t,
8t=50,
解得:t=,
100×=625km.
答:该车最多能行驶625km.
19.①销售量每增加1千克,售价就增加2.1元.②31.5元.
【解析】试题分析:①根据表可以得到:销售量每增加1千克,售价就增加2.1元;
②当x=15时,y的值是2.1元的15倍,据此即可求解.
试题解析:①销售量每增加1千克,售价就增加2.1元.
②当x=15时,y=2.1×15=31.5(元).
点睛:本题考查了函数的表示方法,正确理解销售量每增加1千克,售价就增加2.1元是关键.
20. (324π-1)cm2 (324π-81)cm2
【解析】分析:(1)剩下部分的面积y就是大圆的面积与挖去的正方形的面积的差;
(2)在函数解析式中分别求出半径x,分别是1cm与9cm时,面积的值,即可求解.
本题解析:
(1)y与x之间的关系式为:y= ;
(2)当挖去圆的半径为1cm时,由(1)中求出的函数关系式可得,圆环面积:y=324π-1 =(323π-1)cm ;
当挖去圆的半径为9cm时,圆环面积y=324π-9 =(243π-81)cm ,所以圆环面积由变化(323π-1)cm 到(243π-81)cm .
点睛:本题重点考查了函数关系式的表示方法,圆的面积,正方形的面积,函数的自变量与因变量;解题关键是熟知相关概念;剩下部分的面积y就是大圆的面积与挖去的正方形的面积的差.
21.(1)底边BC的长是常量,DE的长和三角形BEC的面积是变量(2)y=4x(0【解析】试题分析:
(1)由题意可知,点E在AD上由D附近向点A运动的过程中,△BEC的面积和BC边上的高DE发生了变化,是变量;而底边BC没有发生变化,是常量;
(2)由题意和三角形的面积计算方法可得: =S△BEC=BC·DE,由此即可得到与之间的关系式.
试题解析:
(1)由题意可知:底边BC的长是常量,DE的长和△BEC的面积是变量;
(2)由题意可得: BC·DE= ,即 与之间的关系式为: .
22.(1)反映的是电话费和时间两个变量之间的关系,时间是自变量,电话费是因变量;(2) 电话费需付3 元;(3) y=0.6x.
【解析】试题分析:(1)根据函数的定义可知,时间是自变量,电话费是因变量;(2)由图表数据得出打5分钟电话,需要的电话费.(3)由图表数据可知电话费的变化趋势是每分钟缴费0.6元,所以y 与x之间的关系式 y=0.6x.
试题解析:
(1)反映的是电话费和时间两个变量之间的关系,时间是自变量,电话费是因变量;
(2) 电话费需付3 元;
(3) y=0.6x.
点睛:此题主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
3.2 用关系式表示的变量间关系同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.用数学式子表示变量之间的关系的方法叫做关系式法,关系式法是表示变量关系的另一种方法.
2.用关系式表示自变量与因变量之间的关系,在现实生活中有着广泛地应用,同时也是以后学习函数的基础,应注意将因变量写在等式的左边,自变量写在等式的右边.
3. 在用关系式表示变量之间的关系时,要注明自变量的取值范围
①当表达式的分母不含有自变量时,自变量取全体实数.
②当表达式的分母中含有自变量时,自变量取值要使分母不为零.
③对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
基础知识和能力拓展精练
一、选择题
1.已知圆柱的高为3 cm,当圆柱的底面半径r(cm)由小变大时,圆柱的体积V(cm3)随之变化,则V与r的关系式是( )
A. V=πr2 B. V=3πr2 C. V=πr2 D. V=9πr2
2.汽车离开甲站10千米后,以60千米/时的速度匀速前进了小时,则汽车离开甲站所走的路程(千米)与时间(小时)之间的关系式是( )
A. B. C. D.
3.已知齿轮每分钟转 EMBED Equation.DSMT4 转,如果用(转)表示转数, (分)表示转动的时间,那么用表示的关系式为( ).
A. B. C. D.
4.如果每盒钢笔有10支,售价25元,那么购买钢笔的总钱数y(元)与支数x之间的关系式为( )
A. y=10x B. y=25x C. y=x D. y=x
5.李大爷要围成一个长方形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长应恰好为24米,要围成的菜园是如图所示的长方形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的关系式是( )
A. y=-2x+24(0<x<12) B. y=-x+12(0<x<24)
C. y=2x-24(0<x<12) D. y=x-12(0<x<24)
6.某大剧场地面的一部分为扇形,观众席的座位数按下列方式设置:
排数(x) 1 2 3 4 …
座位数(y) 50 53 56 59 …
有下列结论:①排数x是自变量,座位数y是因变量;②排数x是因变量,座位数y是自变量;③y=50+3x;④y=47+3x,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
7.如图,梯形上底长、下底长分别是x,y,高是6,面积是24,则y与x之间的表达式是( )
A. y=﹣x+8 B. y=﹣x+4 C. y=x﹣8 D. y=x﹣4
8.油箱中存油,油从油箱中均匀流出,流速为,则油箱中剩余油量与流出时间的关系式是( ).
A. B. C. D.
9.一个长方形的周长为30,则长方形的面积y与长方形一边长x的关系式为( )
A. y=x(15-x) B. y=x(30-x) C. y=x(30-2x) D. y=x(15+x)
10.某种签字笔的单价为2元,购买这种签字笔x支的总价为y元,则y与x之间的函数关系式为( )
A. y=- EMBED Equation.DSMT4 x B. y=x C. y=-2x D. y=2x
二、填空题
11.宁宁同学设计了一个计算程序如下表:
输入数据 1 2 3 4 5 …
输出数据 …
根据表格中的数据的对应关系,可得出输出数据y与输入数据x之间的关系式为___________.
12.某种储蓄的月利率是0.2%,存入100元本金后,不扣除利息税,本息和y(元)与所存月数x(x为正整数)之间的关系为__________,4个月的本息和为________.
13.李老师带领x名学生到某动物园参观,已知成人票每张20元,学生票每张10元.设门票的总费用为y元,则y=________.
14.若一个长方体底面积为60cm2,高为hcm,则体积V(cm3)与h(cm)的关系式为_____,若h从1cm变化到10cm时,长方体的体积由___cm3变化到___cm3.
15.小雨画了一个边长为3 cm的正方形,如果将正方形的边长增加x cm,那么面积的增加值y(cm2)与边长的增加值x(cm)之间的关系式为____________.
16.如图所示,梯形的上底长是厘米,下底长是厘米,当梯形的高由大变小时,梯形的面积也随之发生变化.
()在这个变化过程中,自变量是__________,因变量是__________.
()梯形的面积与高(厘米)之间的关系式为__________.
()当梯形的高由厘米变化到厘米时,梯形的面积由__________变化到__________.
三、解答题
17.某地区现有果树24000棵,计划今后每年栽果树3000棵.
①试用含年数x(年)的式子表示果树总棵数y(棵);
②预计到第5年该地区有多少棵果树?
18.为了解某种品牌小汽车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h) 0 1 2 3 …
油箱剩余油量Q(L) 100 94 88 82 …
①根据上表的数据,请你写出Q与t的关系式;
②汽车行驶5h后,油箱中的剩余油量是多少?
③该品牌汽车的油箱加满50L,若以100km/h的速度匀速行驶,该车最多能行驶多远?
19.秋天到来了,小明家的苹果获得了丰收,他主动帮助妈妈到集市上去卖刚刚采摘下的苹果.已知销售数量x(千克)与售价y(元)的关系如下表所示:
数量x(千克) 1 2 3 4 5
售价y(元) 2.1 4.2 6.3 8.4 10.5
①根据表格中的数据,售价y是怎样随销售量的变化而变化的?
②求当x=15时,y的值是多少?
20.如图,一个半径为18 cm的圆,从中心挖去一个正方形,当挖去的正方形的边长由小变大时,剩下部分的面积也随之发生变化.
(1)若挖去的正方形边长为x(cm),剩下部分的面积为y(cm2),则y与x之间的关系式是什么
(2)当挖去的正方形的边长由1 cm变化到9 cm时,剩下部分的面积由____变化到____.
21.如图,在三角形ABC中,底边BC=8 cm,高AD=6 cm,点E为AD上一动点,当点E从点D附近向点A运动时,三角形BEC的面积发生了变化.
(1)在这个变化过程中,哪些量是变量 哪些量是常量
(2)如果设DE的长为x cm,三角形BEC的面积为y cm2,那么怎样用含x的式子表示y
22.下表是某公共电话亭打长途电话的几次收费记录:
时间x(分) 1 2 3 4 5 6 7
电话费y(元) 0.6 1.2 1.8 2.4 3.0 3.6 4.2
(1)上表反映了哪两个变量间的关系 哪个是自变量 哪个是因变量
(2)丽丽打了5分钟电话,那么电话费需付多少元
(3)请写出y 与x之间的关系式.
参考答案
1.B
【解析】∵圆柱的体积=底面积×高,该圆柱高为3cm,底面半径为cm,体积为cm3,
∴.
故选B.
2.A
【解析】根据路程与时间的关系,可得函数解析式:s=10+60t,
故选:A.
3.D
【解析】t表示转动的时间,那么在t分钟内齿轮转动的转数为:100t
即n=100t.
故选D.
4.D
【解析】解:25÷10=,所以购买钢笔的总钱数y(元)与支数x之间的关系式为:y=x.故选D.
点睛:此题主要考查了函数关系式的求法,以及单价、数量、总价的关系,要熟练掌握;解答此题的关键是根据单价=总价÷数量,求出每支钢笔的价格是多少.
5.B
【解析】由题意得:2y+x=24,
故可得:y= x+12(0
6.B
【解析】根据图表可知随着排数的增大,座位数也增大.所以排数x是自变量,座位数y是因变量;
根据图标中的数据可得y=47+3x.故①④正确.
则选:B.
7.A
【解析】梯形上底长、下底长分别是x,y,高是6,面积是24,
则y与x之间的表达式是:24=(x+y)×6÷2,
即y=﹣x+8,
故选:A.
8.B
【解析】利用油箱中存油量20升-流出油量=剩余油量, 可得:流出油量是0.2t,
则剩余油量:Q=20 0.2t,故选:B.
9.A
【解析】∵长方形的周长为30,其中一边长为,
∴该长方形的另一边长为: ,
∴该长方形的面积: .
故选A.
10.D
【解析】依题意有:y=2x,
故选D.
11.y=
【解析】解:根据题意,得: .故答案为: .
12. y=100+0.2x 100.8元
【解析】第一个月y=100+100×0.2℅,
第二个月y=100+100×0.2℅+〔100+100×0.2℅〕×0.2℅
结合题干可知y=100(1+0.2℅x )= y=100+0.2x,
令x=4,求得y=100.8.
故答案为: y=100+0.2x;100.8元.
点睛:此题主要考查了函数解析式,根据题意,找到所求量的等量关系是解决问题的关键.
13.10x+20
【解析】根据总费用=成人票用钱数+学生票用钱数,可得y=10x+20.
故答案为:10x+20.
14. V=60h 60 600
【解析】根据长方体的体积=底面积×高,得:V=60h;
当h=1时,V=60,当h=10时,V=600,故长方体的体积由60 cm3变化到600 cm3.
故答案为:V=60h;60;600
15.y=x2+6x
【解析】由题意得y=(3+x)(3+x)-3×3=x +6x.
故答案为:y=x +6x.
16. 梯形的高 梯形的面积 90 9
【解析】(1)自变量是梯形的高,因变量是梯形的面积;
(2)梯形的面积y(cm )与高x(cm)之间的关系式为:y=(5+13)x×=9x;
(3)当梯形的高是l0cm时,y=9×10=90,
当梯形的高是l0cm时,y=9×1=9,
梯形的面积由90cm 变化到9cm .故答案为:梯形的高, 梯形的面积, y=9x, 90, 9.
17.①y=24000+3000x(x≥0,且x为正整数);②预计到第5年该地区有39000棵果树.
【解析】试题分析:①本题的等量关系是:果树的总数=现有的果树的数量+每年栽树的数量×年数,由此可得出关于果树总数与年数的函数关系式;
②根据①即可求出第5年的果树的数量.
试题解析:①根据题意得:y=24000+3000x(x≥0,且x为正整数);
②根据题意得:y=24000+3000x(x≥0,且x为正整数);
当x=5时,y=24000+3000×5=39000.
答:预计到第5年该地区有39000棵果树.
点睛:本题考查了根据实际问题列函数关系式,解题的关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出函数式,然后利用函数关系式即可解决题目的问题.
18.①Q=50﹣8t;②汽车行驶5h后,油箱中的剩余油量是10L;③该车最多能行驶625km.
【解析】试题分析:①由表格可知,开始油箱中的油为50L,每行驶1小时,油量减少8L,据此可得t与Q的关系式;
②求汽车行驶5h后,油箱中的剩余油量即是求当t=5时,Q的值;
③贮满50L汽油的汽车,理论上最多能行驶几小时即是求当Q=0时,t的值.
试题解析①Q与t的关系式为:Q=50﹣8t;
②当t=5时,Q=50﹣8×5=10,
答:汽车行驶5h后,油箱中的剩余油量是10L;
③当Q=0时,0=50﹣8t,
8t=50,
解得:t=,
100×=625km.
答:该车最多能行驶625km.
19.①销售量每增加1千克,售价就增加2.1元.②31.5元.
【解析】试题分析:①根据表可以得到:销售量每增加1千克,售价就增加2.1元;
②当x=15时,y的值是2.1元的15倍,据此即可求解.
试题解析:①销售量每增加1千克,售价就增加2.1元.
②当x=15时,y=2.1×15=31.5(元).
点睛:本题考查了函数的表示方法,正确理解销售量每增加1千克,售价就增加2.1元是关键.
20. (324π-1)cm2 (324π-81)cm2
【解析】分析:(1)剩下部分的面积y就是大圆的面积与挖去的正方形的面积的差;
(2)在函数解析式中分别求出半径x,分别是1cm与9cm时,面积的值,即可求解.
本题解析:
(1)y与x之间的关系式为:y= ;
(2)当挖去圆的半径为1cm时,由(1)中求出的函数关系式可得,圆环面积:y=324π-1 =(323π-1)cm ;
当挖去圆的半径为9cm时,圆环面积y=324π-9 =(243π-81)cm ,所以圆环面积由变化(323π-1)cm 到(243π-81)cm .
点睛:本题重点考查了函数关系式的表示方法,圆的面积,正方形的面积,函数的自变量与因变量;解题关键是熟知相关概念;剩下部分的面积y就是大圆的面积与挖去的正方形的面积的差.
21.(1)底边BC的长是常量,DE的长和三角形BEC的面积是变量(2)y=4x(0
(1)由题意可知,点E在AD上由D附近向点A运动的过程中,△BEC的面积和BC边上的高DE发生了变化,是变量;而底边BC没有发生变化,是常量;
(2)由题意和三角形的面积计算方法可得: =S△BEC=BC·DE,由此即可得到与之间的关系式.
试题解析:
(1)由题意可知:底边BC的长是常量,DE的长和△BEC的面积是变量;
(2)由题意可得: BC·DE= ,即 与之间的关系式为: .
22.(1)反映的是电话费和时间两个变量之间的关系,时间是自变量,电话费是因变量;(2) 电话费需付3 元;(3) y=0.6x.
【解析】试题分析:(1)根据函数的定义可知,时间是自变量,电话费是因变量;(2)由图表数据得出打5分钟电话,需要的电话费.(3)由图表数据可知电话费的变化趋势是每分钟缴费0.6元,所以y 与x之间的关系式 y=0.6x.
试题解析:
(1)反映的是电话费和时间两个变量之间的关系,时间是自变量,电话费是因变量;
(2) 电话费需付3 元;
(3) y=0.6x.
点睛:此题主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
