广西陆川县中学2017-2018学年高二下学期开学考试数学(文)试卷
文档属性
| 名称 | 广西陆川县中学2017-2018学年高二下学期开学考试数学(文)试卷 |

|
|
| 格式 | zip | ||
| 文件大小 | 153.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-06 00:00:00 | ||
图片预览


文档简介
广西陆川县中学2018年春季期高二开学基础知识竞赛试卷
文科数学
(命题人: 审题人:)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在复平面内,复数对应的点为,复数,若复数,则复数对应的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.有一段演绎推理是这样的:“指数函数都是增函数;已知是指数函数;则是增函数”的结论显然是错误的,这是因为
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
3.用反证法证明:若整系数一元二次方程有有理数根,那么a、b、c中至少有一个是偶数.用反证法证明时,下列假设正确的是( )
A.假设a、b、c都不是偶数 B.假设a、b、c都是偶数
C.假设a、b、c至多有一个偶数 D.假设a、b、c至多有两个偶数
4.已知△中,,求证.
证明: ,,画线部分是演绎推理的( ).
A.大前提 B.三段论 C.结论 D. 小前提
5.已知椭圆(0A.1 B.3 C.6 D.8
6.若p,q为简单命题,则“p且q为假”是“p或q为假”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.在极坐标系中,圆的圆心的极坐标为( )
A. B. C. D.
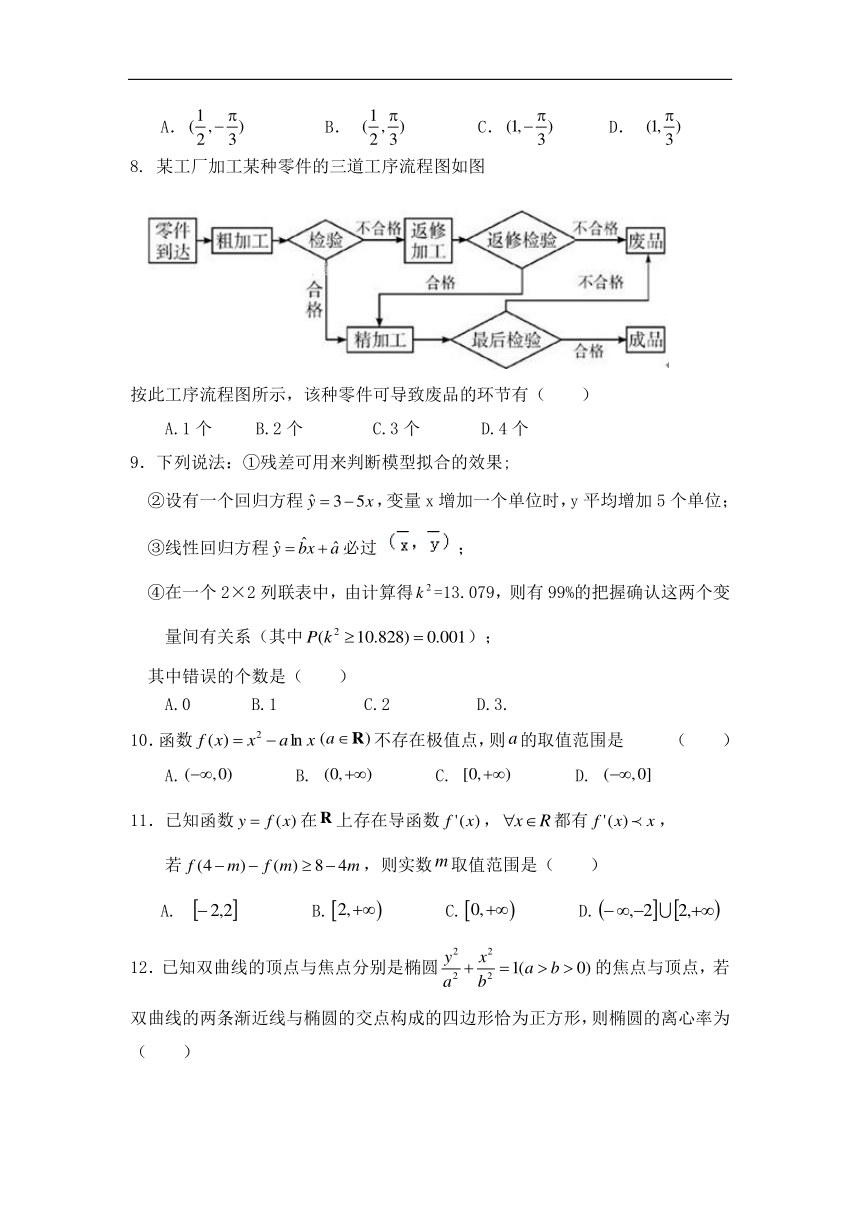
8. 某工厂加工某种零件的三道工序流程图如图
按此工序流程图所示,该种零件可导致废品的环节有( )
A.1个 B.2个 C.3个 D.4个
下列说法:①残差可用来判断模型拟合的效果;
②设有一个回归方程,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程必过;
④在一个2×2列联表中,由计算得=13.079,则有99%的把握确认这两个变量间有关系(其中);
其中错误的个数是( )
A.0 B.1 C.2 D.3.
10.函数不存在极值点,则的取值范围是 ( )
A. B. C. D.
11.已知函数在上存在导函数,都有,
若,则实数取值范围是( )
B. C. D.
12.已知双曲线的顶点与焦点分别是椭圆的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.若,,则 .
14. 已知数列的前项和为,则数列的通项公式为 .
15.若不等式的解集为,则不等式的解集为 .
16.已知直线,是之间的一定点,并且点到的距离分别为1,2,是直线上一动点,,与直线交于点,则面积的最小值为 .
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本大题满分10分)
已知复数z=3+bi(b∈R),且(1+3i)·z为纯虚数.
(1)求复数z及;
(2)若ω=,求复数ω的模|ω|.
18.已知数列满足递推式,其中
(1)求;
(2)求证:数列为等比数列.
19.在中,内角的对边分别为,已知.
(1)求;
(2)若,,求的面积.
20.(本小题满分12分)
已知以点为圆心的圆与直线相切,过点的动直线与圆相交于两点.
(1)求圆的方程;
(2)当时,求直线的方程.
21.如图,在四棱锥P-ABCD中,AB//CD,且
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,,且四棱锥P-ABCD的体积为,求该四棱锥的侧面积.
22.(本小题满分12分)
已知不等式x2-5ax+b>0的解集为{x|x>4或x<1}
(1)求实数a,b的值;
(2)若0<x<1,f(x)=,求f(x)的最小值.
文科数学答案
1-6.A A ADBC 7--12 ABBDBA
13.1; 14.; 15.; 16.2.
17.解析: (1)(1+3i)·(3+bi)=(3-3b)+(9+b)i
∵(1+3i)·z是纯虚数,
∴3-3b=0,且9+b≠0,
∴b=1,∴z=3+i.
(2)ω==
==-i
∴|ω|==.
18.解:(1)由知
解得同理得
(2)由知
是以为首项以2为公比的等比数列
19. 解:(1)解法1:由及正弦定理可得
. ………………2分
在中,,所以
………………4分
由以上两式得,即, ……………5分
又,所以. …………6分
(2)的面积, ………………7分
由,及余弦定理得
, ……………………8分
因为,所以,
即 , …………………10分
故的面积. …………………12分
20.解:(1)由题意知到直线的距离为圆半径
2分
圆的方程为 4分
(2)设线段的中点为,连结,则由垂径定理可知,且,在中由勾股定理易知 6分
当动直线的斜率不存在时,直线的方程为时,显然满足题意; 7分
当动直线的斜率存在时,设动直线的方程为: 8分
由到动直线的距离为1得 10分
或为所求方程. 12分
21.(1)证明:∵ ,∵
∴∵∴
(2)由①知∵,
取AD中点O,所以 ,
∴∴AO=2
∴∴
=
22.解:(1)根据题意,不等式x2-5ax+b>0的解集为{x|x>4或x<1},
则方程x2-5ax+b=0的两个根是1和4,
则有5a=1+4,b=1×4,
即a=1,b=4;
(2)由(1)知,
因为0<x<1,所以0<1-x<1,所以
所以==9
当且仅当,即时,等号成立.所以f(x)的最小值为9.
文科数学
(命题人: 审题人:)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在复平面内,复数对应的点为,复数,若复数,则复数对应的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.有一段演绎推理是这样的:“指数函数都是增函数;已知是指数函数;则是增函数”的结论显然是错误的,这是因为
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
3.用反证法证明:若整系数一元二次方程有有理数根,那么a、b、c中至少有一个是偶数.用反证法证明时,下列假设正确的是( )
A.假设a、b、c都不是偶数 B.假设a、b、c都是偶数
C.假设a、b、c至多有一个偶数 D.假设a、b、c至多有两个偶数
4.已知△中,,求证.
证明: ,,画线部分是演绎推理的( ).
A.大前提 B.三段论 C.结论 D. 小前提
5.已知椭圆(0
6.若p,q为简单命题,则“p且q为假”是“p或q为假”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.在极坐标系中,圆的圆心的极坐标为( )
A. B. C. D.
8. 某工厂加工某种零件的三道工序流程图如图
按此工序流程图所示,该种零件可导致废品的环节有( )
A.1个 B.2个 C.3个 D.4个
下列说法:①残差可用来判断模型拟合的效果;
②设有一个回归方程,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程必过;
④在一个2×2列联表中,由计算得=13.079,则有99%的把握确认这两个变量间有关系(其中);
其中错误的个数是( )
A.0 B.1 C.2 D.3.
10.函数不存在极值点,则的取值范围是 ( )
A. B. C. D.
11.已知函数在上存在导函数,都有,
若,则实数取值范围是( )
B. C. D.
12.已知双曲线的顶点与焦点分别是椭圆的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.若,,则 .
14. 已知数列的前项和为,则数列的通项公式为 .
15.若不等式的解集为,则不等式的解集为 .
16.已知直线,是之间的一定点,并且点到的距离分别为1,2,是直线上一动点,,与直线交于点,则面积的最小值为 .
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本大题满分10分)
已知复数z=3+bi(b∈R),且(1+3i)·z为纯虚数.
(1)求复数z及;
(2)若ω=,求复数ω的模|ω|.
18.已知数列满足递推式,其中
(1)求;
(2)求证:数列为等比数列.
19.在中,内角的对边分别为,已知.
(1)求;
(2)若,,求的面积.
20.(本小题满分12分)
已知以点为圆心的圆与直线相切,过点的动直线与圆相交于两点.
(1)求圆的方程;
(2)当时,求直线的方程.
21.如图,在四棱锥P-ABCD中,AB//CD,且
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,,且四棱锥P-ABCD的体积为,求该四棱锥的侧面积.
22.(本小题满分12分)
已知不等式x2-5ax+b>0的解集为{x|x>4或x<1}
(1)求实数a,b的值;
(2)若0<x<1,f(x)=,求f(x)的最小值.
文科数学答案
1-6.A A ADBC 7--12 ABBDBA
13.1; 14.; 15.; 16.2.
17.解析: (1)(1+3i)·(3+bi)=(3-3b)+(9+b)i
∵(1+3i)·z是纯虚数,
∴3-3b=0,且9+b≠0,
∴b=1,∴z=3+i.
(2)ω==
==-i
∴|ω|==.
18.解:(1)由知
解得同理得
(2)由知
是以为首项以2为公比的等比数列
19. 解:(1)解法1:由及正弦定理可得
. ………………2分
在中,,所以
………………4分
由以上两式得,即, ……………5分
又,所以. …………6分
(2)的面积, ………………7分
由,及余弦定理得
, ……………………8分
因为,所以,
即 , …………………10分
故的面积. …………………12分
20.解:(1)由题意知到直线的距离为圆半径
2分
圆的方程为 4分
(2)设线段的中点为,连结,则由垂径定理可知,且,在中由勾股定理易知 6分
当动直线的斜率不存在时,直线的方程为时,显然满足题意; 7分
当动直线的斜率存在时,设动直线的方程为: 8分
由到动直线的距离为1得 10分
或为所求方程. 12分
21.(1)证明:∵ ,∵
∴∵∴
(2)由①知∵,
取AD中点O,所以 ,
∴∴AO=2
∴∴
=
22.解:(1)根据题意,不等式x2-5ax+b>0的解集为{x|x>4或x<1},
则方程x2-5ax+b=0的两个根是1和4,
则有5a=1+4,b=1×4,
即a=1,b=4;
(2)由(1)知,
因为0<x<1,所以0<1-x<1,所以
所以==9
当且仅当,即时,等号成立.所以f(x)的最小值为9.
同课章节目录
