第五章 相交线与平行线压轴题解析
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
相交线与平行线
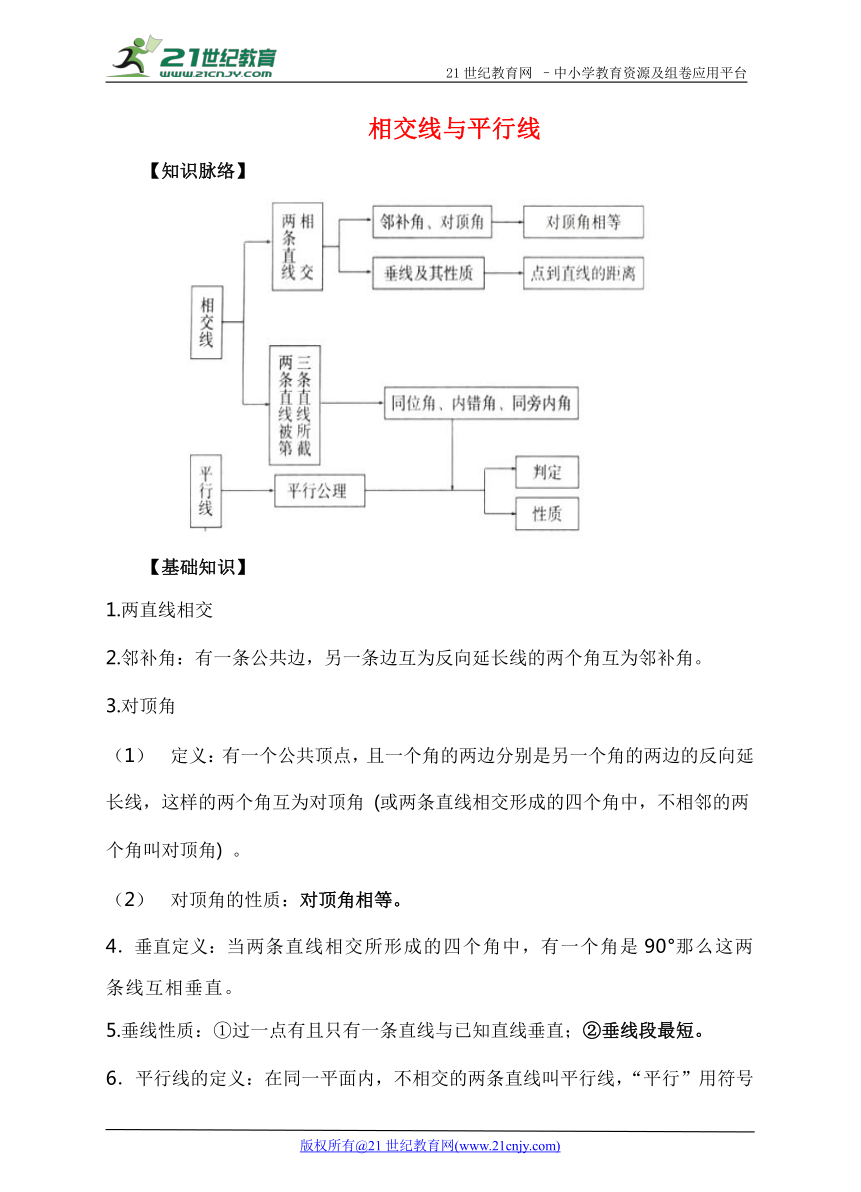
【知识脉络】
( http: / / www.21cnjy.com )
【基础知识】
1.两直线相交
2.邻补角:有一条公共边,另一条边互为反向延长线的两个角互为邻补角。
3.对顶角
(1) 定义:有一个公共顶点,且一个角的两边分别 ( http: / / www.21cnjy.com )是另一个角的两边的反向延长线,这样的两个角互为对顶角 (或两条直线相交形成的四个角中,不相邻的两个角叫对顶角) 。2·1·c·n·j·y
(2) 对顶角的性质:对顶角相等。
4.垂直定义:当两条直线相交所形成的四个角中,有一个角是90°那么这两条线互相垂直。
5.垂线性质:①过一点有且只有一条直线与已知直线垂直;②垂线段最短。
6.平行线的定义:在同一平面内,不相交的两条直线叫平行线,“平行”用符号“∥”表示,如直线a,b是平行线,可记作“a∥b”【出处:21教育名师】
7.平行公理及推论
(1)平行公理:过已知直线外一点有且只有一条直线与已知直线平行。
(2)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
注:
(1)平行公理中的“有且只有”包含两层意思:一是存在性;二是唯一性。
(2)平行具有传递性,即如果a∥b,b∥c,则a∥c。
8.两条直线的位置关系:在同一平面内,两条直线的位置关系有相交和平行。
9.平行线的性质:
(1)两直线平行,同位角相等(在同一平面内)
(2)两直线平行,内错角相等(在同一平面内)
(3)两直线平行,同旁内角互补(在同一平面内)
10.平行线的判定
(1)同位角相等,两直线平行;(在同一平面内)
(2)内错角相等,两直线平行;(在同一平面内)
(3)同旁内角互补,两直线平行;(在同一平面内)
(4)如果两条直线都和第三条直线平行,那么这两条直线也互相平行;
补充:
(5)平行的定义;(在同一平面内)
(6)在同一平面内,垂直于同一直线的两直线平行。
11.平移的定义及特征
定义:将一个图形向某个方向平行移动,叫做图形的平移。
特征:①平移前后的两个图形形状、大小完全一样;
②平移前与平移后两个图形的对应点连线平行且相等。
【典例解析】
例题1:如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间的关系并说出理由;
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合)
( http: / / www.21cnjy.com )
【考点】平行线的性质.
【分析】(1)过点P作l1的平行线,根据平行线的性质进行解题.(2)(3)都是同样的道理.
【解答】解:(1)∠1+∠2=∠3;
理由:过点P作l1的平行线,
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠1=∠4,∠2=∠5,(两直线平行,内错角相等)
∵∠4+∠5=∠3,
∴∠1+∠2=∠3;
(2)同(1)可证:∠1+∠2=∠3;
(3)∠1﹣∠2=∠3或∠2﹣∠1=∠3
理由:当点P在下侧时,过点P作l1的平行线PQ,
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠2=∠4,∠1=∠3+∠4,(两直线平行,内错角相等)
∴∠1﹣∠2=∠3;
当点P在上侧时,同理可得:∠2﹣∠1=∠3.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
例题2:(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系并说明理由;21·世纪*教育网
(2)如图2,当∠M=90°且AB与CD的 ( http: / / www.21cnjy.com )位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,G为线段AC上一定点,点H为 ( http: / / www.21cnjy.com )直线CD上一动点且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外)∠CGH+∠CHG与∠BAC有何数量关系?猜想结论并说明理由.21*cnjy*com
( http: / / www.21cnjy.com )
【考点】平行线的判定与性质.
【分析】(1)根据角平分线的性质和三角形内角和定理即可得出答案;
(2)过M作MF∥AB,根 ( http: / / www.21cnjy.com )据平行线的性质得出∠BAM=∠AMF,∠FMC=∠DCM,再根据∠M=90°,即可得出∠BAM+∠MCD=90°;【版权所有:21教育】
(3)过点G作GP∥AB,根据平行线的性质得出∠BAC=∠PGC,∠CHG=∠PGH,从而得出∠BAC=∠CHG+∠CGH.21教育名师原创作品
【解答】解:(1)∵CM平分∠ACD,AM平分∠BAC,
∴∠BAC=2∠MAC,∠ACD=2∠ACM,
∵∠MAC+∠ACM=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAM+∠MCD=90°;
理由:如图2,过M作MF∥AB,
∵AB∥CD,
∴MF∥AB∥CD,
∴∠BAM=∠AMF,∠FMC=∠DCM,
∵∠M=90°,
∴∠BAM+∠MCD=90°;
(3)过点G作GP∥AB,
∵AB∥CD
∴GP∥CD,
∴∠BAC=∠PGC,∠CHG=∠PGH,
∴∠PGC=∠CHG+∠CGH,
∴∠BAC=∠CHG+∠CGH.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
例题3:下列各图中的MA1与NAn平行.
(1)图①中的∠A1+∠A2= 180 度,图②中的∠A1+∠A2+∠A3= 360 度,
图③中的∠A1+∠A2+∠A3+∠A4= 540 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 720 度,…,21*cnjy*com
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10= 1620 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An= (n﹣1)180° .
( http: / / www.21cnjy.com )
【考点】平行线的性质.
【分析】(1)①根据两直线平行,同旁内角互补求解即可;②③④⑩分别过拐点作MA1的平行线,然后根据两直线平行,同旁内角互补解答;
(2)根据(1)中的计算规律,不难发现为180°的倍数,然后根据脚码的变化规律写出即可.
【解答】解:(1)图①中,∵MA1∥NA2,
∴∠A1+∠A2=180°,
如图,分别过A2、A3、A4作MA1的平行线,
图②中的∠A1+∠A2+∠A3=360°,
图③中的∠A1+∠A2+∠A3+∠A4=540°,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5=720°,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10=1620°;
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An=(n﹣1)180°.
故答案为:180,360,540,720,1620;(n﹣1)180°.
( http: / / www.21cnjy.com )
【点评】本题考查了两直线平行,同旁内角互补的性质,过拐点作辅助线利用平行线的性质是解题的关键.
例题4:如图,已知AB∥CD,EF与AB、CD分别相交于点E、F,∠BEF与∠EFD的平分线相交于点P,求证:EP⊥FP.21·cn·jy·com
( http: / / www.21cnjy.com )
【考点】三角形内角和定理;角平分线的定义;平行线的性质.
【分析】要证EP⊥FP,即证∠PEF+∠EFP=90°,由角平分线的性质和平行线的性质可知,∠PEF+∠EFP= ( http: / / www.21cnjy.com )(∠BEF+∠EFD)=90°.
【解答】证明:∵AB∥CD,
∴∠BEF+∠EFD=180°,
又EP、FP分别是∠BEF、∠EFD的平分线,
∴∠PEF= ( http: / / www.21cnjy.com )∠BEF,∠EFP= ( http: / / www.21cnjy.com )∠EFD,
∴∠PEF+∠EFP= ( http: / / www.21cnjy.com )(∠BEF+∠EFD)=90°,
∴∠P=180°﹣(∠PEF+∠EFP)=180°﹣90°=90°,
即EP⊥FP.
【点评】本题的关键就是找到∠PEF+∠EFP与∠BEF+∠EFD之间的关系,考查了整体代换思想.
【跟踪训练】
1. 如图,AD∥BC,∠1=∠C,∠B=60°.
(1)求∠C的度数;
(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
( http: / / www.21cnjy.com )
2. 如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
( http: / / www.21cnjy.com )
3. 探索:小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A、∠的数量关系.21世纪教育网版权所有
发现:在图1中,小明和小亮都发现:∠APC=∠A+∠C;
( http: / / www.21cnjy.com )
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A( 两直线平行,内错角相等 )
∵PQ∥AB,AB∥CD.
∴PQ∥CD( 平行于同一直线的两直线平行 )
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 小明的证法 .
应用:
在图2中,若∠A=120°,∠C=140°,则∠P的度数为 100° ;
在图3中,若∠A=30°,∠C=70°,则∠P的度数为 40° ;
拓展:
在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
4. 已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
5. 如图,已知直线l1∥l2,l3、 ( http: / / www.21cnjy.com )l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.
( http: / / www.21cnjy.com )
6. 小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点 ( http: / / www.21cnjy.com )A、M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
( http: / / www.21cnjy.com )
请问小坚的提示中①是∠ 2 ,④是∠ AMD .
理由②是: 两直线平行,内错角相等 ;
理由③是: 角平分线定义 ;
∠CMD的度数是 21 °.
参考答案:
1. 如图,AD∥BC,∠1=∠C,∠B=60°.
(1)求∠C的度数;
(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
( http: / / www.21cnjy.com )
【考点】平行线的判定与性质.
【分析】(1)根据平行线的性质和已知求出∠C=∠1=∠B,即可得出答案;
(2)求出∠1=∠B=60°,根据平行线的性质求出∠ADC,求出∠ADE,即可得出∠1=∠ADE,根据平行线的判定得出即可.【来源:21·世纪·教育·网】
【解答】解:(1)∵AD∥BC,
∴∠1=∠B,
∵∠1=∠C,∠B=60°,
∴∠C=∠B=60°;
(2)DE∥AB,
理由是:∵AD∥BC,∠B=60°,
∴∠1=∠B=60°,
∵AD∥BC,∠C=60°,
∴∠ADC=180°﹣∠C120°,
∵DE平分∠ADC,
∴∠ADE= ( http: / / www.21cnjy.com )∠ADC=60°,
∴∠1=∠ADE,
∴DE∥AB.
【点评】本题考查了平行线的性质和判定的应用,能综合运用定理进行推理是解此题的关键.
2. 如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
( http: / / www.21cnjy.com )
【考点】平行线的判定.
【分析】设AB与DE相交于H,若判 ( http: / / www.21cnjy.com )断ED与FB的位置关系,首先要判断∠1和∠EHA的大小;由∠3=∠4可证得BD∥CF(内错角相等,两直线平行),可得到∠5=∠BAF;已知∠5=∠6,等量代换后发现AB∥CD,即∠2=∠EHA,由此可得到∠1=∠EHA,根据同位角相等,两直线平行即可判断出BF、DE的位置关系.
【解答】解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
又∵∠5=∠6,
∴∠BAF=∠6,
∴AB∥CD,
∴∠2=∠EHA,
又∵∠1=∠2,即∠1=∠EHA,
∴BF∥DE.
另解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
∵∠5=∠6,
∴∠BAF=∠6,
∵△BFA、△DEC的内角和都是180°
∴△BFA=∠1+∠BFA+BAF;△DEC=∠2+∠4+∠6
∵∠1=∠2;∠BAF=∠6
∴∠BFA=∠4,
∴BF∥DE.
( http: / / www.21cnjy.com )
3. 探索:小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A、∠的数量关系.21教育网
发现:在图1中,小明和小亮都发现:∠APC=∠A+∠C;
( http: / / www.21cnjy.com )
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A( 两直线平行,内错角相等 )
∵PQ∥AB,AB∥CD.
∴PQ∥CD( 平行于同一直线的两直线平行 )
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 小明的证法 .
应用:
在图2中,若∠A=120°,∠C=140°,则∠P的度数为 100° ;
在图3中,若∠A=30°,∠C=70°,则∠P的度数为 40° ;
拓展:
在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
【考点】平行线的判定与性质.
【分析】过点P作AB的平行线,用相似的证明方法运用平行线的性质进行证明即可.
【解答】解:如图1,过点P作PQ∥AB,
( http: / / www.21cnjy.com )
∴∠APQ=∠A(两直线平行,内错角相等)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(平行于同一直线的两直线平行)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C,
故两人的证明过程中,完全正确的是小明的证法;
如图2,过点P作PE∥AB,
∴∠APE+∠A=180°,∠A=120°,
∴∠APE=60°,
∵PE∥AB,AB∥CD.
∴PE∥CD(平行于同一直线的两直线平行)
∴∠CPE+∠C=180°,∠C=140°,
∴∠CPE=40°,
∴∠APC=∠APE+∠CPE
=100°;
如图3,过点P作PF∥AB,
∴∠APF=∠A,
∵PF∥AB,AB∥CD.
∴PF∥CD,
∴∠CPF=∠C
∴∠CPF﹣∠APF=∠C﹣∠A
即∠APC=∠C﹣∠A=40°;
如图4,过点P作PG∥AB,
∴∠APG+∠A=180°,
∴∠APG=180°﹣∠A
∵PG∥AB,AB∥CD,
∴PG∥CD,(平行于同一直线的两直线平行)
∴∠CPG+∠C=180°,
∴∠CPG=180°﹣∠C
∴∠APC=∠CPG﹣∠APG=∠A﹣∠C.
故答案为:两直线平行,内错角相等;平行于同一直线的两直线平行;小明的证法;100°;40°.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
4. 已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.www.21-cn-jy.com
( http: / / www.21cnjy.com )
【考点】平行线的判定与性质;垂线.
【分析】先结合图形猜想BF与AC的位置关系是 ( http: / / www.21cnjy.com ):BF⊥AC.要证BF⊥AC,只要证得DE∥BF即可,由平行线的判定可知只需证∠2+∠3=180°,根据平行线的性质结合已知条件即可求证.21cnjy.com
【解答】证明:BF与AC的位置关系是:BF⊥AC.
理由:∵∠AGF=∠ABC,
∴BC∥GF(同位角相等,两直线平行),
∴∠1=∠3;
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE;
∵DE⊥AC,
∴BF⊥AC.
( http: / / www.21cnjy.com )
5. 如图,已知直线l1∥ ( http: / / www.21cnjy.com )l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.
( http: / / www.21cnjy.com )
【考点】平行线的性质.
【分析】此题三个小题的解 ( http: / / www.21cnjy.com )题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.2-1-c-n-j-y
【解答】证明:(1)过P作PQ∥l1∥l2,
由两直线平行,内错角相等,可得:
∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPE+∠QPF,
∴∠3=∠1+∠2.
(2)关系:∠3=∠2﹣∠1;
过P作直线PQ∥l1∥l2,
则:∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPF﹣∠QPE,
∴∠3=∠2﹣∠1.
(3)关系:∠3=360°﹣∠1﹣∠2.
过P作PQ∥l1∥l2;
同(1)可证得:∠3=∠CEP+∠DFP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠CEP+∠DFP+∠1+∠2=360°,
即∠3=360°﹣∠1﹣∠2.
( http: / / www.21cnjy.com )
6. 小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点A、 ( http: / / www.21cnjy.com )M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.www-2-1-cnjy-com
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
( http: / / www.21cnjy.com )
请问小坚的提示中①是∠ 2 ,④是∠ AMD .
理由②是: 两直线平行,内错角相等 ;
理由③是: 角平分线定义 ;
∠CMD的度数是 21 °.
【考点】平行线的性质.
【分析】根据两直线平行,内错角相等可得 ( http: / / www.21cnjy.com )∠1=∠AMD=28°,∠2=∠DMB=70°,进而可得∠AMB,再根据角平分线定义可得∠BMC的度数,然后可得答案.
【解答】解:∵l1∥l2∥l3,
∴∠1=∠AMD=28°,∠2=∠DMB=70°(两直线平行,内错角相等),
∴∠AMB=28°+70°=98°,
∵MC平分∠AMB,
∴∠BMC= ( http: / / www.21cnjy.com )∠AMB=98°× ( http: / / www.21cnjy.com )=49°(角平分线定义),
∴∠DMC=70°﹣49°=21°,
故答案为:2;AMD;两直线平行,内错角相等;角平分线定义;
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
相交线与平行线
【知识脉络】
( http: / / www.21cnjy.com )
【基础知识】
1.两直线相交
2.邻补角:有一条公共边,另一条边互为反向延长线的两个角互为邻补角。
3.对顶角
(1) 定义:有一个公共顶点,且一个角的两边分别 ( http: / / www.21cnjy.com )是另一个角的两边的反向延长线,这样的两个角互为对顶角 (或两条直线相交形成的四个角中,不相邻的两个角叫对顶角) 。2·1·c·n·j·y
(2) 对顶角的性质:对顶角相等。
4.垂直定义:当两条直线相交所形成的四个角中,有一个角是90°那么这两条线互相垂直。
5.垂线性质:①过一点有且只有一条直线与已知直线垂直;②垂线段最短。
6.平行线的定义:在同一平面内,不相交的两条直线叫平行线,“平行”用符号“∥”表示,如直线a,b是平行线,可记作“a∥b”【出处:21教育名师】
7.平行公理及推论
(1)平行公理:过已知直线外一点有且只有一条直线与已知直线平行。
(2)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行。
注:
(1)平行公理中的“有且只有”包含两层意思:一是存在性;二是唯一性。
(2)平行具有传递性,即如果a∥b,b∥c,则a∥c。
8.两条直线的位置关系:在同一平面内,两条直线的位置关系有相交和平行。
9.平行线的性质:
(1)两直线平行,同位角相等(在同一平面内)
(2)两直线平行,内错角相等(在同一平面内)
(3)两直线平行,同旁内角互补(在同一平面内)
10.平行线的判定
(1)同位角相等,两直线平行;(在同一平面内)
(2)内错角相等,两直线平行;(在同一平面内)
(3)同旁内角互补,两直线平行;(在同一平面内)
(4)如果两条直线都和第三条直线平行,那么这两条直线也互相平行;
补充:
(5)平行的定义;(在同一平面内)
(6)在同一平面内,垂直于同一直线的两直线平行。
11.平移的定义及特征
定义:将一个图形向某个方向平行移动,叫做图形的平移。
特征:①平移前后的两个图形形状、大小完全一样;
②平移前与平移后两个图形的对应点连线平行且相等。
【典例解析】
例题1:如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
(1)试找出∠1、∠2、∠3之间的关系并说出理由;
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合)
( http: / / www.21cnjy.com )
【考点】平行线的性质.
【分析】(1)过点P作l1的平行线,根据平行线的性质进行解题.(2)(3)都是同样的道理.
【解答】解:(1)∠1+∠2=∠3;
理由:过点P作l1的平行线,
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠1=∠4,∠2=∠5,(两直线平行,内错角相等)
∵∠4+∠5=∠3,
∴∠1+∠2=∠3;
(2)同(1)可证:∠1+∠2=∠3;
(3)∠1﹣∠2=∠3或∠2﹣∠1=∠3
理由:当点P在下侧时,过点P作l1的平行线PQ,
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠2=∠4,∠1=∠3+∠4,(两直线平行,内错角相等)
∴∠1﹣∠2=∠3;
当点P在上侧时,同理可得:∠2﹣∠1=∠3.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
例题2:(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系并说明理由;21·世纪*教育网
(2)如图2,当∠M=90°且AB与CD的 ( http: / / www.21cnjy.com )位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,G为线段AC上一定点,点H为 ( http: / / www.21cnjy.com )直线CD上一动点且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外)∠CGH+∠CHG与∠BAC有何数量关系?猜想结论并说明理由.21*cnjy*com
( http: / / www.21cnjy.com )
【考点】平行线的判定与性质.
【分析】(1)根据角平分线的性质和三角形内角和定理即可得出答案;
(2)过M作MF∥AB,根 ( http: / / www.21cnjy.com )据平行线的性质得出∠BAM=∠AMF,∠FMC=∠DCM,再根据∠M=90°,即可得出∠BAM+∠MCD=90°;【版权所有:21教育】
(3)过点G作GP∥AB,根据平行线的性质得出∠BAC=∠PGC,∠CHG=∠PGH,从而得出∠BAC=∠CHG+∠CGH.21教育名师原创作品
【解答】解:(1)∵CM平分∠ACD,AM平分∠BAC,
∴∠BAC=2∠MAC,∠ACD=2∠ACM,
∵∠MAC+∠ACM=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD;
(2)∠BAM+∠MCD=90°;
理由:如图2,过M作MF∥AB,
∵AB∥CD,
∴MF∥AB∥CD,
∴∠BAM=∠AMF,∠FMC=∠DCM,
∵∠M=90°,
∴∠BAM+∠MCD=90°;
(3)过点G作GP∥AB,
∵AB∥CD
∴GP∥CD,
∴∠BAC=∠PGC,∠CHG=∠PGH,
∴∠PGC=∠CHG+∠CGH,
∴∠BAC=∠CHG+∠CGH.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
例题3:下列各图中的MA1与NAn平行.
(1)图①中的∠A1+∠A2= 180 度,图②中的∠A1+∠A2+∠A3= 360 度,
图③中的∠A1+∠A2+∠A3+∠A4= 540 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 720 度,…,21*cnjy*com
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10= 1620 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An= (n﹣1)180° .
( http: / / www.21cnjy.com )
【考点】平行线的性质.
【分析】(1)①根据两直线平行,同旁内角互补求解即可;②③④⑩分别过拐点作MA1的平行线,然后根据两直线平行,同旁内角互补解答;
(2)根据(1)中的计算规律,不难发现为180°的倍数,然后根据脚码的变化规律写出即可.
【解答】解:(1)图①中,∵MA1∥NA2,
∴∠A1+∠A2=180°,
如图,分别过A2、A3、A4作MA1的平行线,
图②中的∠A1+∠A2+∠A3=360°,
图③中的∠A1+∠A2+∠A3+∠A4=540°,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5=720°,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10=1620°;
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An=(n﹣1)180°.
故答案为:180,360,540,720,1620;(n﹣1)180°.
( http: / / www.21cnjy.com )
【点评】本题考查了两直线平行,同旁内角互补的性质,过拐点作辅助线利用平行线的性质是解题的关键.
例题4:如图,已知AB∥CD,EF与AB、CD分别相交于点E、F,∠BEF与∠EFD的平分线相交于点P,求证:EP⊥FP.21·cn·jy·com
( http: / / www.21cnjy.com )
【考点】三角形内角和定理;角平分线的定义;平行线的性质.
【分析】要证EP⊥FP,即证∠PEF+∠EFP=90°,由角平分线的性质和平行线的性质可知,∠PEF+∠EFP= ( http: / / www.21cnjy.com )(∠BEF+∠EFD)=90°.
【解答】证明:∵AB∥CD,
∴∠BEF+∠EFD=180°,
又EP、FP分别是∠BEF、∠EFD的平分线,
∴∠PEF= ( http: / / www.21cnjy.com )∠BEF,∠EFP= ( http: / / www.21cnjy.com )∠EFD,
∴∠PEF+∠EFP= ( http: / / www.21cnjy.com )(∠BEF+∠EFD)=90°,
∴∠P=180°﹣(∠PEF+∠EFP)=180°﹣90°=90°,
即EP⊥FP.
【点评】本题的关键就是找到∠PEF+∠EFP与∠BEF+∠EFD之间的关系,考查了整体代换思想.
【跟踪训练】
1. 如图,AD∥BC,∠1=∠C,∠B=60°.
(1)求∠C的度数;
(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
( http: / / www.21cnjy.com )
2. 如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
( http: / / www.21cnjy.com )
3. 探索:小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A、∠的数量关系.21世纪教育网版权所有
发现:在图1中,小明和小亮都发现:∠APC=∠A+∠C;
( http: / / www.21cnjy.com )
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A( 两直线平行,内错角相等 )
∵PQ∥AB,AB∥CD.
∴PQ∥CD( 平行于同一直线的两直线平行 )
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 小明的证法 .
应用:
在图2中,若∠A=120°,∠C=140°,则∠P的度数为 100° ;
在图3中,若∠A=30°,∠C=70°,则∠P的度数为 40° ;
拓展:
在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
4. 已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com )
5. 如图,已知直线l1∥l2,l3、 ( http: / / www.21cnjy.com )l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.
( http: / / www.21cnjy.com )
6. 小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点 ( http: / / www.21cnjy.com )A、M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
( http: / / www.21cnjy.com )
请问小坚的提示中①是∠ 2 ,④是∠ AMD .
理由②是: 两直线平行,内错角相等 ;
理由③是: 角平分线定义 ;
∠CMD的度数是 21 °.
参考答案:
1. 如图,AD∥BC,∠1=∠C,∠B=60°.
(1)求∠C的度数;
(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
( http: / / www.21cnjy.com )
【考点】平行线的判定与性质.
【分析】(1)根据平行线的性质和已知求出∠C=∠1=∠B,即可得出答案;
(2)求出∠1=∠B=60°,根据平行线的性质求出∠ADC,求出∠ADE,即可得出∠1=∠ADE,根据平行线的判定得出即可.【来源:21·世纪·教育·网】
【解答】解:(1)∵AD∥BC,
∴∠1=∠B,
∵∠1=∠C,∠B=60°,
∴∠C=∠B=60°;
(2)DE∥AB,
理由是:∵AD∥BC,∠B=60°,
∴∠1=∠B=60°,
∵AD∥BC,∠C=60°,
∴∠ADC=180°﹣∠C120°,
∵DE平分∠ADC,
∴∠ADE= ( http: / / www.21cnjy.com )∠ADC=60°,
∴∠1=∠ADE,
∴DE∥AB.
【点评】本题考查了平行线的性质和判定的应用,能综合运用定理进行推理是解此题的关键.
2. 如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
( http: / / www.21cnjy.com )
【考点】平行线的判定.
【分析】设AB与DE相交于H,若判 ( http: / / www.21cnjy.com )断ED与FB的位置关系,首先要判断∠1和∠EHA的大小;由∠3=∠4可证得BD∥CF(内错角相等,两直线平行),可得到∠5=∠BAF;已知∠5=∠6,等量代换后发现AB∥CD,即∠2=∠EHA,由此可得到∠1=∠EHA,根据同位角相等,两直线平行即可判断出BF、DE的位置关系.
【解答】解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
又∵∠5=∠6,
∴∠BAF=∠6,
∴AB∥CD,
∴∠2=∠EHA,
又∵∠1=∠2,即∠1=∠EHA,
∴BF∥DE.
另解:BF、DE互相平行;
理由:如图;
∵∠3=∠4,
∴BD∥CF,
∴∠5=∠BAF,
∵∠5=∠6,
∴∠BAF=∠6,
∵△BFA、△DEC的内角和都是180°
∴△BFA=∠1+∠BFA+BAF;△DEC=∠2+∠4+∠6
∵∠1=∠2;∠BAF=∠6
∴∠BFA=∠4,
∴BF∥DE.
( http: / / www.21cnjy.com )
3. 探索:小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A、∠的数量关系.21教育网
发现:在图1中,小明和小亮都发现:∠APC=∠A+∠C;
( http: / / www.21cnjy.com )
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A( 两直线平行,内错角相等 )
∵PQ∥AB,AB∥CD.
∴PQ∥CD( 平行于同一直线的两直线平行 )
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 小明的证法 .
应用:
在图2中,若∠A=120°,∠C=140°,则∠P的度数为 100° ;
在图3中,若∠A=30°,∠C=70°,则∠P的度数为 40° ;
拓展:
在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
【考点】平行线的判定与性质.
【分析】过点P作AB的平行线,用相似的证明方法运用平行线的性质进行证明即可.
【解答】解:如图1,过点P作PQ∥AB,
( http: / / www.21cnjy.com )
∴∠APQ=∠A(两直线平行,内错角相等)
∵PQ∥AB,AB∥CD.
∴PQ∥CD(平行于同一直线的两直线平行)
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C,
故两人的证明过程中,完全正确的是小明的证法;
如图2,过点P作PE∥AB,
∴∠APE+∠A=180°,∠A=120°,
∴∠APE=60°,
∵PE∥AB,AB∥CD.
∴PE∥CD(平行于同一直线的两直线平行)
∴∠CPE+∠C=180°,∠C=140°,
∴∠CPE=40°,
∴∠APC=∠APE+∠CPE
=100°;
如图3,过点P作PF∥AB,
∴∠APF=∠A,
∵PF∥AB,AB∥CD.
∴PF∥CD,
∴∠CPF=∠C
∴∠CPF﹣∠APF=∠C﹣∠A
即∠APC=∠C﹣∠A=40°;
如图4,过点P作PG∥AB,
∴∠APG+∠A=180°,
∴∠APG=180°﹣∠A
∵PG∥AB,AB∥CD,
∴PG∥CD,(平行于同一直线的两直线平行)
∴∠CPG+∠C=180°,
∴∠CPG=180°﹣∠C
∴∠APC=∠CPG﹣∠APG=∠A﹣∠C.
故答案为:两直线平行,内错角相等;平行于同一直线的两直线平行;小明的证法;100°;40°.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
4. 已知如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.www.21-cn-jy.com
( http: / / www.21cnjy.com )
【考点】平行线的判定与性质;垂线.
【分析】先结合图形猜想BF与AC的位置关系是 ( http: / / www.21cnjy.com ):BF⊥AC.要证BF⊥AC,只要证得DE∥BF即可,由平行线的判定可知只需证∠2+∠3=180°,根据平行线的性质结合已知条件即可求证.21cnjy.com
【解答】证明:BF与AC的位置关系是:BF⊥AC.
理由:∵∠AGF=∠ABC,
∴BC∥GF(同位角相等,两直线平行),
∴∠1=∠3;
又∵∠1+∠2=180°,
∴∠2+∠3=180°,
∴BF∥DE;
∵DE⊥AC,
∴BF⊥AC.
( http: / / www.21cnjy.com )
5. 如图,已知直线l1∥ ( http: / / www.21cnjy.com )l2,l3、l4和l1、l2分别交于点A、B、C、D,点P 在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.
(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
(2)若点P在图(2)位置时,请直接写出∠1、∠2、∠3之间的关系;
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系并给予证明.
( http: / / www.21cnjy.com )
【考点】平行线的性质.
【分析】此题三个小题的解 ( http: / / www.21cnjy.com )题思路是一致的,过P作直线l1、l2的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.2-1-c-n-j-y
【解答】证明:(1)过P作PQ∥l1∥l2,
由两直线平行,内错角相等,可得:
∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPE+∠QPF,
∴∠3=∠1+∠2.
(2)关系:∠3=∠2﹣∠1;
过P作直线PQ∥l1∥l2,
则:∠1=∠QPE、∠2=∠QPF;
∵∠3=∠QPF﹣∠QPE,
∴∠3=∠2﹣∠1.
(3)关系:∠3=360°﹣∠1﹣∠2.
过P作PQ∥l1∥l2;
同(1)可证得:∠3=∠CEP+∠DFP;
∵∠CEP+∠1=180°,∠DFP+∠2=180°,
∴∠CEP+∠DFP+∠1+∠2=360°,
即∠3=360°﹣∠1﹣∠2.
( http: / / www.21cnjy.com )
6. 小明同学在做作业时,遇到这样一道几何题:
已知:如图1,l1∥l2∥l3,点A、 ( http: / / www.21cnjy.com )M、B分别在直线l1,l2,l3上,MC平分∠AMB,∠1=28°,∠2=70°.求:∠CMD的度数.www-2-1-cnjy-com
小明想了许久没有思路,就去请教好朋友小坚,小坚给了他如图2所示的提示:
( http: / / www.21cnjy.com )
请问小坚的提示中①是∠ 2 ,④是∠ AMD .
理由②是: 两直线平行,内错角相等 ;
理由③是: 角平分线定义 ;
∠CMD的度数是 21 °.
【考点】平行线的性质.
【分析】根据两直线平行,内错角相等可得 ( http: / / www.21cnjy.com )∠1=∠AMD=28°,∠2=∠DMB=70°,进而可得∠AMB,再根据角平分线定义可得∠BMC的度数,然后可得答案.
【解答】解:∵l1∥l2∥l3,
∴∠1=∠AMD=28°,∠2=∠DMB=70°(两直线平行,内错角相等),
∴∠AMB=28°+70°=98°,
∵MC平分∠AMB,
∴∠BMC= ( http: / / www.21cnjy.com )∠AMB=98°× ( http: / / www.21cnjy.com )=49°(角平分线定义),
∴∠DMC=70°﹣49°=21°,
故答案为:2;AMD;两直线平行,内错角相等;角平分线定义;
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
