第九章 不等式与不等式组压轴题解析
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
不等式与不等式组
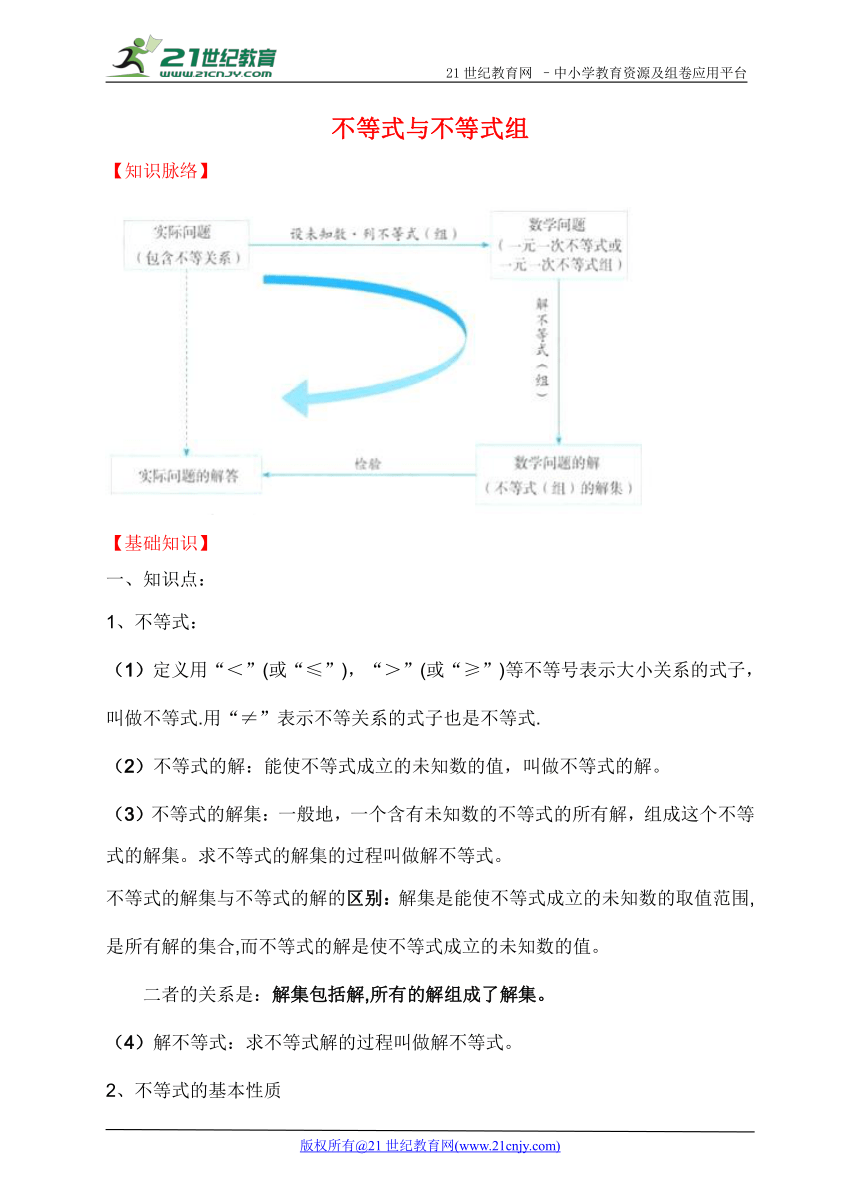
【知识脉络】
( http: / / www.21cnjy.com )
【基础知识】
一、知识点:
1、不等式:
(1)定义用“<”(或“≤”),“>”( ( http: / / www.21cnjy.com )或“≥”)等不等号表示大小关系的式子,叫做不等式.用“≠”表示不等关系的式子也是不等式.
(2)不等式的解:能使不等式成立的未知数的值,叫做不等式的解。
(3)不等式的解集:一般地,一个含有未知数的不等式的所有解,组成这个不等式的解集。求不等式的解集的过程叫做解不等式。21cnjy.com
不等式的解集与不等式的解的区别:解集是能使不等式成立的未知数的取值范围,是所有解的集合,而不等式的解是使不等式成立的未知数的值。
二者的关系是:解集包括解,所有的解组成了解集。
(4)解不等式:求不等式解的过程叫做解不等式。
2、不等式的基本性质
性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变。 即:如果,那么.
性质2:不等式的两边都乘上(或除以)同一个正数,不等号的方向不变。 即:如果,并且,那么;.
性质3:不等式的两边都乘上(或除以)同一个负数,不等号的方向改变。 即:如果,并且,那么;.21·cn·jy·com
性质4:如果,那么.(对称性)
性质5:如果,,那么.(传递性)
(二)一元一次不等式
1、定义:含有一个未知数,未知数的次数是1,且不等号两边都是整式的不等式,叫做一元一次不等式。【来源:21·世纪·教育·网】
2.一元一次不等式的解法:
根据是不等式的 ( http: / / www.21cnjy.com )基本性质;一般步骤为:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
解不等式应注意:①去分母时,每一项都要乘同一个数,尤其不要漏乘常数项;②移项时不要忘记变号;③去括号时,若括号前面是负号,括号里的每一项都要变号;④在不等式两边都乘(或除以)同一个负数时,不等号的方向要改变。
3.不等式的解集在数轴上表示:
(1)边界:有等号的是实心圆圈,无等号的是空心圆圈;【版权所有:21教育】
(2)方向:大向右,小向左
(三)一元一次不等式组
1、定义:有几个含有同一个未知数的一元一次不等式组成的不等式组,叫做一元一次不等式组
2、(一元一次)不等式组的解集:这几个不等式解集的公共部分,叫做这个(一元一次)不等式组的解集。
3、解不等式组:求不等式组解集的过程,叫做解不等式组。
4、一元一次不等式组的解法
1)分别求出不等式组中各个不等式的解集
2)利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集。
由两个一元一次不等式组成的不等式组的解集可归纳为下面四种情况:
不等式组 解集 口诀记忆
同大取大
同小取小
大小小大中间找
无解 大大小小则无解
(四)一元一次不等式(组)解决实际问题
解题的步骤:
⑴审题,找出不等关系→ ⑵设未知数→ ⑶列出不等式(组)→
⑷求出不等式的解集→ ⑸找出符合题意的值→ ⑹作答。
二、解题技巧
1、有解无解问题:
(1)(2)
(3)
2、特征解问题:
解题步骤:把原式中的要求的量(以下简记为) 当作已知数,去解原式——→得到原式的解(含)——→根据解的特征列出式子(关于的式子)——→解出的值。2·1·c·n·j·y
【典例解析】
例题1:感知:解不等式 ( http: / / www.21cnjy.com )>0.根据两数相除,同号得正,异号得负,得不等式组① ( http: / / www.21cnjy.com ),或不等式组② ( http: / / www.21cnjy.com ).解不等式组①,得x>1;解不等式组②,得x<﹣2,所以原不等式的解集为x>1或x<﹣2.2-1-c-n-j-y
探究:解不等式 ( http: / / www.21cnjy.com )<0.
应用:不等式(x﹣3)(x+5)≤0的解集是 ﹣5≤x≤3 .
【考点】解一元一次不等式组.
【分析】(1)先把不等式转化为不等式组,然后通过解不等式组来求分式不等式;
(2)先把不等式转化为不等式组,然后通过解不等式组来求不等式.
【解答】解:探究:原不等式可化为不等式组① ( http: / / www.21cnjy.com )或不等式组② ( http: / / www.21cnjy.com ),
解不等式组①,得无解.
解不等式组②,得:﹣1<x<2.
所以原不等式的解集为﹣1<x<2.
应用:原不等式可化为不等式组:① ( http: / / www.21cnjy.com )或② ( http: / / www.21cnjy.com ),
解不等式组①得:不等式组无解,
解不等式组②得:﹣5≤x≤3.
故答案为:﹣5≤x≤3.
例题2:若关于x的不等式mx﹣n>0的解集是x< ( http: / / www.21cnjy.com ),则关于x的不等式(m+n)x>n﹣m的解集是( )21教育网
A.x<﹣ ( http: / / www.21cnjy.com ) B.x>﹣ ( http: / / www.21cnjy.com ) C.x< ( http: / / www.21cnjy.com ) D.x> ( http: / / www.21cnjy.com )
【考点】解一元一次不等式;不等式的解集.
【分析】先解关于x的不等式mx﹣n>0,得出解集,再根据不等式的解集是x< ( http: / / www.21cnjy.com ),从而得出m与n的关系,然后解不等式(m+n)x>n﹣m即可.
【解答】解:∵关于x的不等式mx﹣n>0的解集是x< ( http: / / www.21cnjy.com ),
∴m<0, ( http: / / www.21cnjy.com ) = ( http: / / www.21cnjy.com ),
解得m=3n,
∴n<0,
∴解关于x的不等式(m+n)x>n﹣m得,x< ( http: / / www.21cnjy.com ),
∴x< ( http: / / www.21cnjy.com )=﹣ ( http: / / www.21cnjy.com ),
故选:A.
例题3:仔细观察下图,认真阅读对话 ( http: / / www.21cnjy.com )
根据对话的内容,试求出饼干和牛奶的标价各是多少元?
【考点】一元一次不等式组的应用.
【分析】设饼干的标价是x元/袋,(x是整数)牛奶的标价是y元/袋,由题意得 ( http: / / www.21cnjy.com ),用整体代入的思想求出x的取值,注意为整数且小于10,代入②可求牛奶的价格.www.21-cn-jy.com
【解答】解:设饼干的标价是x元/袋,(x是整数)牛奶的标价是y元/袋,由题意得
( http: / / www.21cnjy.com ),
由②得y=9.2﹣0.9x③
③代入①得x+9.2﹣0.9x>10
∴x>8
∵x是整数且小于10
∴x=9
∴把x=9代入③得y=9.2﹣0.9×9=1.1(元)
答:饼干的标价是9元/盒,牛奶的标价是1.1元/袋.
例题4:某学校准备购买若干个足球和篮球(每 ( http: / / www.21cnjy.com )个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.21·世纪*教育网
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?www-2-1-cnjy-com
【考点】二元一次方程组的应用.
【分析】(1)设购买一个足 ( http: / / www.21cnjy.com )球需要x元,购买一个篮球需要y元,根据购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元,列方程组求解;21*cnjy*com
(2)设购买a个篮球,则购买(96﹣a)个足球,根据总费用不超过5720元,列不等式求出最大整数解.【出处:21教育名师】
【解答】解:(1)设购买一个足球需要x元,购买一个篮球需要y元,
根据题意得: ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com ),
答:购买一个足球需要50元,购买一个篮球需要80元;
(2)设购买a个篮球,则购买(96﹣a)个足球,
根据题意得:80a+50(96﹣a)≤5720,
解得:a≤ ( http: / / www.21cnjy.com ),
∵a是整数,
∴a≤30,
答:最多可以购买30个篮球.
【点评】本题考查了二元一次方程组的应用和一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系和不等关系,列方程和不等式求解.
【跟踪训练】
1. 为了节省空间,家里的饭碗一般是摆 ( http: / / www.21cnjy.com )起来存放的,如果6只饭碗(注:饭碗的大小形状都一样,下同)摆起来的高度为15cm,9只饭碗摆起来的高度为20cm,李老师家的碗橱每格的高度为36cm,则李老师一摞碗最多只能放 只.
2. 对于任意实数m,n定义一种新 ( http: / / www.21cnjy.com )运算m※n=mn﹣m+3,等式的右边是通常的加减法和乘法运算,例如:3※5=3×5﹣3+3=15.请根据上述定义解决问题:若a<2※x<7,且解集中恰有两个整数解,求a的取值范围.21*cnjy*com
3. “全名阅读”深入人心,好读书 ( http: / / www.21cnjy.com ),读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1560元,20本文学名著比20本动漫书多360元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于74本,总费用不超过2100,请求出所有符合条件的购书方案.
4. 星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) 售价(元/台)
电饭煲 200 250
电压锅 160 200
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ( http: / / www.21cnjy.com ),问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
参考答案:
1. 为了节省空间,家里的饭碗一般是摆起来存 ( http: / / www.21cnjy.com )放的,如果6只饭碗(注:饭碗的大小形状都一样,下同)摆起来的高度为15cm,9只饭碗摆起来的高度为20cm,李老师家的碗橱每格的高度为36cm,则李老师一摞碗最多只能放 18 只.
【考点】一元一次不等式的应用.
【分析】设碗底的高度为xc ( http: / / www.21cnjy.com )m,碗身的高度为ycm,可得碗的高度和碗的个数的关系式为高度=个数×碗底高度+碗身高度,根据6只饭碗摞起来的高度为15cm,9只饭碗摞起来的高度为20cm,列方程组求解,根据碗橱每格的高度为36cm,列不等式求解.
【解答】解:设碗底的高度为xcm,碗身的高度为ycm,
由题意得, ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com ),
设李老师一摞碗能放a只碗,
( http: / / www.21cnjy.com )a+5≤36,
解得:a≤ ( http: / / www.21cnjy.com ),
故李老师一摞碗最多只能放18只碗.
故答案为18.
2. 对于任意实数m,n ( http: / / www.21cnjy.com )定义一种新运算m※n=mn﹣m+3,等式的右边是通常的加减法和乘法运算,例如:3※5=3×5﹣3+3=15.请根据上述定义解决问题:若a<2※x<7,且解集中恰有两个整数解,求a的取值范围.【来源:21cnj*y.co*m】
【考点】不等式的解集;实数的运算.
【分析】根据定义可知:2※x=2x﹣2+3=2x+1,利用不等式可求解出 ( http: / / www.21cnjy.com )<x<3,由于x有两个整数解,所以0≤ ( http: / / www.21cnjy.com )<1,求出该不等式的解集即可知道a的取值范围.
【解答】解:由题意可知:2※x=2x﹣2+3=2x+1,
∵a<2※x<7,
∴a<2x+1<7,
∴ ( http: / / www.21cnjy.com )<x<3,
∵该不等式的解集有两个整数解,
∴该整数解为1或2,
∴0≤ ( http: / / www.21cnjy.com )<1,
∴1≤a<3.
3. “全名阅读”深入人心,好读书,读 ( http: / / www.21cnjy.com )好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1560元,20本文学名著比20本动漫书多360元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于74本,总费用不超过2100,请求出所有符合条件的购书方案.
【考点】一元一次不等式组的应用;二元一次方程组的应用.
【分析】(1)设每本文学名著x元,动漫书y元,根据题意列出方程组解答即可;
(2)根据学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于74本,总费用不超过2100元,列出不等式组,解答即可.
【解答】解:(1)设每本文学名著x元,动漫书y元,
可得: ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com ),
答:每本文学名著和动漫书各为38元和20元;
(2)设学校要求购买文学名著x本,动漫书为(x+20)本,根据题意可得:
( http: / / www.21cnjy.com ),
解得:26≤x≤ ( http: / / www.21cnjy.com ),
因为取整数,
所以x取27,28,29;
方案一:文学名著27本,动漫书47本;
方案二:文学名著28本,动漫书48本;
方案三:文学名著29本,动漫书49本.
4. 星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) 售价(元/台)
电饭煲 200 250
电压锅 160 200
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?21世纪教育网版权所有
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ( http: / / www.21cnjy.com ),问橱具店有哪几种进货方案?并说明理由;21教育名师原创作品
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
【考点】一元一次不等式组的应用;二元一次方程组的应用.
【分析】(1)设橱具店购进电饭煲x台, ( http: / / www.21cnjy.com )电压锅y台,根据图表中的数据列出关于x、y的方程组并解答即可,等量关系是:这两种电器共30台;共用去了5600元;
(2)设购买电饭煲a台,则购买电压锅(50﹣a)台,根据“用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ( http: / / www.21cnjy.com )”列出不等式组;
(3)结合(2)中的数据进行计算.
【解答】解:(1)设橱具店购进电饭煲x台,电压锅y台,依题意得
( http: / / www.21cnjy.com ),
解得 ( http: / / www.21cnjy.com ),
所以,20×+10×=1400(元).
答:橱具店在该买卖中赚了1400元;
(2)设购买电饭煲a台,则购买电压锅(50﹣a)台,依题意得
( http: / / www.21cnjy.com ),
解得 22 ( http: / / www.21cnjy.com )≤a≤25.
又∵a为正整数,∴a可取23,24,25.
故有三种方案:①防购买电饭煲23台,则购买电压锅27台;
②购买电饭煲24台,则购买电压锅26台;
③购买电饭煲25台,则购买电压锅25台.
(3)设橱具店赚钱数额为W元,
当a=23时,W=23×+27×=2230;
当a=24时,W=24×+26×=2240;
当a=25时,W=25×+25×=2250;
综上所述,当a=25时,W最大,此时购进电饭煲、电压锅各25台.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
不等式与不等式组
【知识脉络】
( http: / / www.21cnjy.com )
【基础知识】
一、知识点:
1、不等式:
(1)定义用“<”(或“≤”),“>”( ( http: / / www.21cnjy.com )或“≥”)等不等号表示大小关系的式子,叫做不等式.用“≠”表示不等关系的式子也是不等式.
(2)不等式的解:能使不等式成立的未知数的值,叫做不等式的解。
(3)不等式的解集:一般地,一个含有未知数的不等式的所有解,组成这个不等式的解集。求不等式的解集的过程叫做解不等式。21cnjy.com
不等式的解集与不等式的解的区别:解集是能使不等式成立的未知数的取值范围,是所有解的集合,而不等式的解是使不等式成立的未知数的值。
二者的关系是:解集包括解,所有的解组成了解集。
(4)解不等式:求不等式解的过程叫做解不等式。
2、不等式的基本性质
性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变。 即:如果,那么.
性质2:不等式的两边都乘上(或除以)同一个正数,不等号的方向不变。 即:如果,并且,那么;.
性质3:不等式的两边都乘上(或除以)同一个负数,不等号的方向改变。 即:如果,并且,那么;.21·cn·jy·com
性质4:如果,那么.(对称性)
性质5:如果,,那么.(传递性)
(二)一元一次不等式
1、定义:含有一个未知数,未知数的次数是1,且不等号两边都是整式的不等式,叫做一元一次不等式。【来源:21·世纪·教育·网】
2.一元一次不等式的解法:
根据是不等式的 ( http: / / www.21cnjy.com )基本性质;一般步骤为:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)系数化为1.
解不等式应注意:①去分母时,每一项都要乘同一个数,尤其不要漏乘常数项;②移项时不要忘记变号;③去括号时,若括号前面是负号,括号里的每一项都要变号;④在不等式两边都乘(或除以)同一个负数时,不等号的方向要改变。
3.不等式的解集在数轴上表示:
(1)边界:有等号的是实心圆圈,无等号的是空心圆圈;【版权所有:21教育】
(2)方向:大向右,小向左
(三)一元一次不等式组
1、定义:有几个含有同一个未知数的一元一次不等式组成的不等式组,叫做一元一次不等式组
2、(一元一次)不等式组的解集:这几个不等式解集的公共部分,叫做这个(一元一次)不等式组的解集。
3、解不等式组:求不等式组解集的过程,叫做解不等式组。
4、一元一次不等式组的解法
1)分别求出不等式组中各个不等式的解集
2)利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集。
由两个一元一次不等式组成的不等式组的解集可归纳为下面四种情况:
不等式组 解集 口诀记忆
同大取大
同小取小
大小小大中间找
无解 大大小小则无解
(四)一元一次不等式(组)解决实际问题
解题的步骤:
⑴审题,找出不等关系→ ⑵设未知数→ ⑶列出不等式(组)→
⑷求出不等式的解集→ ⑸找出符合题意的值→ ⑹作答。
二、解题技巧
1、有解无解问题:
(1)(2)
(3)
2、特征解问题:
解题步骤:把原式中的要求的量(以下简记为) 当作已知数,去解原式——→得到原式的解(含)——→根据解的特征列出式子(关于的式子)——→解出的值。2·1·c·n·j·y
【典例解析】
例题1:感知:解不等式 ( http: / / www.21cnjy.com )>0.根据两数相除,同号得正,异号得负,得不等式组① ( http: / / www.21cnjy.com ),或不等式组② ( http: / / www.21cnjy.com ).解不等式组①,得x>1;解不等式组②,得x<﹣2,所以原不等式的解集为x>1或x<﹣2.2-1-c-n-j-y
探究:解不等式 ( http: / / www.21cnjy.com )<0.
应用:不等式(x﹣3)(x+5)≤0的解集是 ﹣5≤x≤3 .
【考点】解一元一次不等式组.
【分析】(1)先把不等式转化为不等式组,然后通过解不等式组来求分式不等式;
(2)先把不等式转化为不等式组,然后通过解不等式组来求不等式.
【解答】解:探究:原不等式可化为不等式组① ( http: / / www.21cnjy.com )或不等式组② ( http: / / www.21cnjy.com ),
解不等式组①,得无解.
解不等式组②,得:﹣1<x<2.
所以原不等式的解集为﹣1<x<2.
应用:原不等式可化为不等式组:① ( http: / / www.21cnjy.com )或② ( http: / / www.21cnjy.com ),
解不等式组①得:不等式组无解,
解不等式组②得:﹣5≤x≤3.
故答案为:﹣5≤x≤3.
例题2:若关于x的不等式mx﹣n>0的解集是x< ( http: / / www.21cnjy.com ),则关于x的不等式(m+n)x>n﹣m的解集是( )21教育网
A.x<﹣ ( http: / / www.21cnjy.com ) B.x>﹣ ( http: / / www.21cnjy.com ) C.x< ( http: / / www.21cnjy.com ) D.x> ( http: / / www.21cnjy.com )
【考点】解一元一次不等式;不等式的解集.
【分析】先解关于x的不等式mx﹣n>0,得出解集,再根据不等式的解集是x< ( http: / / www.21cnjy.com ),从而得出m与n的关系,然后解不等式(m+n)x>n﹣m即可.
【解答】解:∵关于x的不等式mx﹣n>0的解集是x< ( http: / / www.21cnjy.com ),
∴m<0, ( http: / / www.21cnjy.com ) = ( http: / / www.21cnjy.com ),
解得m=3n,
∴n<0,
∴解关于x的不等式(m+n)x>n﹣m得,x< ( http: / / www.21cnjy.com ),
∴x< ( http: / / www.21cnjy.com )=﹣ ( http: / / www.21cnjy.com ),
故选:A.
例题3:仔细观察下图,认真阅读对话 ( http: / / www.21cnjy.com )
根据对话的内容,试求出饼干和牛奶的标价各是多少元?
【考点】一元一次不等式组的应用.
【分析】设饼干的标价是x元/袋,(x是整数)牛奶的标价是y元/袋,由题意得 ( http: / / www.21cnjy.com ),用整体代入的思想求出x的取值,注意为整数且小于10,代入②可求牛奶的价格.www.21-cn-jy.com
【解答】解:设饼干的标价是x元/袋,(x是整数)牛奶的标价是y元/袋,由题意得
( http: / / www.21cnjy.com ),
由②得y=9.2﹣0.9x③
③代入①得x+9.2﹣0.9x>10
∴x>8
∵x是整数且小于10
∴x=9
∴把x=9代入③得y=9.2﹣0.9×9=1.1(元)
答:饼干的标价是9元/盒,牛奶的标价是1.1元/袋.
例题4:某学校准备购买若干个足球和篮球(每 ( http: / / www.21cnjy.com )个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.21·世纪*教育网
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?www-2-1-cnjy-com
【考点】二元一次方程组的应用.
【分析】(1)设购买一个足 ( http: / / www.21cnjy.com )球需要x元,购买一个篮球需要y元,根据购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元,列方程组求解;21*cnjy*com
(2)设购买a个篮球,则购买(96﹣a)个足球,根据总费用不超过5720元,列不等式求出最大整数解.【出处:21教育名师】
【解答】解:(1)设购买一个足球需要x元,购买一个篮球需要y元,
根据题意得: ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com ),
答:购买一个足球需要50元,购买一个篮球需要80元;
(2)设购买a个篮球,则购买(96﹣a)个足球,
根据题意得:80a+50(96﹣a)≤5720,
解得:a≤ ( http: / / www.21cnjy.com ),
∵a是整数,
∴a≤30,
答:最多可以购买30个篮球.
【点评】本题考查了二元一次方程组的应用和一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系和不等关系,列方程和不等式求解.
【跟踪训练】
1. 为了节省空间,家里的饭碗一般是摆 ( http: / / www.21cnjy.com )起来存放的,如果6只饭碗(注:饭碗的大小形状都一样,下同)摆起来的高度为15cm,9只饭碗摆起来的高度为20cm,李老师家的碗橱每格的高度为36cm,则李老师一摞碗最多只能放 只.
2. 对于任意实数m,n定义一种新 ( http: / / www.21cnjy.com )运算m※n=mn﹣m+3,等式的右边是通常的加减法和乘法运算,例如:3※5=3×5﹣3+3=15.请根据上述定义解决问题:若a<2※x<7,且解集中恰有两个整数解,求a的取值范围.21*cnjy*com
3. “全名阅读”深入人心,好读书 ( http: / / www.21cnjy.com ),读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1560元,20本文学名著比20本动漫书多360元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于74本,总费用不超过2100,请求出所有符合条件的购书方案.
4. 星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) 售价(元/台)
电饭煲 200 250
电压锅 160 200
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ( http: / / www.21cnjy.com ),问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
参考答案:
1. 为了节省空间,家里的饭碗一般是摆起来存 ( http: / / www.21cnjy.com )放的,如果6只饭碗(注:饭碗的大小形状都一样,下同)摆起来的高度为15cm,9只饭碗摆起来的高度为20cm,李老师家的碗橱每格的高度为36cm,则李老师一摞碗最多只能放 18 只.
【考点】一元一次不等式的应用.
【分析】设碗底的高度为xc ( http: / / www.21cnjy.com )m,碗身的高度为ycm,可得碗的高度和碗的个数的关系式为高度=个数×碗底高度+碗身高度,根据6只饭碗摞起来的高度为15cm,9只饭碗摞起来的高度为20cm,列方程组求解,根据碗橱每格的高度为36cm,列不等式求解.
【解答】解:设碗底的高度为xcm,碗身的高度为ycm,
由题意得, ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com ),
设李老师一摞碗能放a只碗,
( http: / / www.21cnjy.com )a+5≤36,
解得:a≤ ( http: / / www.21cnjy.com ),
故李老师一摞碗最多只能放18只碗.
故答案为18.
2. 对于任意实数m,n ( http: / / www.21cnjy.com )定义一种新运算m※n=mn﹣m+3,等式的右边是通常的加减法和乘法运算,例如:3※5=3×5﹣3+3=15.请根据上述定义解决问题:若a<2※x<7,且解集中恰有两个整数解,求a的取值范围.【来源:21cnj*y.co*m】
【考点】不等式的解集;实数的运算.
【分析】根据定义可知:2※x=2x﹣2+3=2x+1,利用不等式可求解出 ( http: / / www.21cnjy.com )<x<3,由于x有两个整数解,所以0≤ ( http: / / www.21cnjy.com )<1,求出该不等式的解集即可知道a的取值范围.
【解答】解:由题意可知:2※x=2x﹣2+3=2x+1,
∵a<2※x<7,
∴a<2x+1<7,
∴ ( http: / / www.21cnjy.com )<x<3,
∵该不等式的解集有两个整数解,
∴该整数解为1或2,
∴0≤ ( http: / / www.21cnjy.com )<1,
∴1≤a<3.
3. “全名阅读”深入人心,好读书,读 ( http: / / www.21cnjy.com )好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1560元,20本文学名著比20本动漫书多360元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于74本,总费用不超过2100,请求出所有符合条件的购书方案.
【考点】一元一次不等式组的应用;二元一次方程组的应用.
【分析】(1)设每本文学名著x元,动漫书y元,根据题意列出方程组解答即可;
(2)根据学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于74本,总费用不超过2100元,列出不等式组,解答即可.
【解答】解:(1)设每本文学名著x元,动漫书y元,
可得: ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com ),
答:每本文学名著和动漫书各为38元和20元;
(2)设学校要求购买文学名著x本,动漫书为(x+20)本,根据题意可得:
( http: / / www.21cnjy.com ),
解得:26≤x≤ ( http: / / www.21cnjy.com ),
因为取整数,
所以x取27,28,29;
方案一:文学名著27本,动漫书47本;
方案二:文学名著28本,动漫书48本;
方案三:文学名著29本,动漫书49本.
4. 星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) 售价(元/台)
电饭煲 200 250
电压锅 160 200
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?21世纪教育网版权所有
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ( http: / / www.21cnjy.com ),问橱具店有哪几种进货方案?并说明理由;21教育名师原创作品
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
【考点】一元一次不等式组的应用;二元一次方程组的应用.
【分析】(1)设橱具店购进电饭煲x台, ( http: / / www.21cnjy.com )电压锅y台,根据图表中的数据列出关于x、y的方程组并解答即可,等量关系是:这两种电器共30台;共用去了5600元;
(2)设购买电饭煲a台,则购买电压锅(50﹣a)台,根据“用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的 ( http: / / www.21cnjy.com )”列出不等式组;
(3)结合(2)中的数据进行计算.
【解答】解:(1)设橱具店购进电饭煲x台,电压锅y台,依题意得
( http: / / www.21cnjy.com ),
解得 ( http: / / www.21cnjy.com ),
所以,20×+10×=1400(元).
答:橱具店在该买卖中赚了1400元;
(2)设购买电饭煲a台,则购买电压锅(50﹣a)台,依题意得
( http: / / www.21cnjy.com ),
解得 22 ( http: / / www.21cnjy.com )≤a≤25.
又∵a为正整数,∴a可取23,24,25.
故有三种方案:①防购买电饭煲23台,则购买电压锅27台;
②购买电饭煲24台,则购买电压锅26台;
③购买电饭煲25台,则购买电压锅25台.
(3)设橱具店赚钱数额为W元,
当a=23时,W=23×+27×=2230;
当a=24时,W=24×+26×=2240;
当a=25时,W=25×+25×=2250;
综上所述,当a=25时,W最大,此时购进电饭煲、电压锅各25台.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
