第六章 实数压轴题解析
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
实数
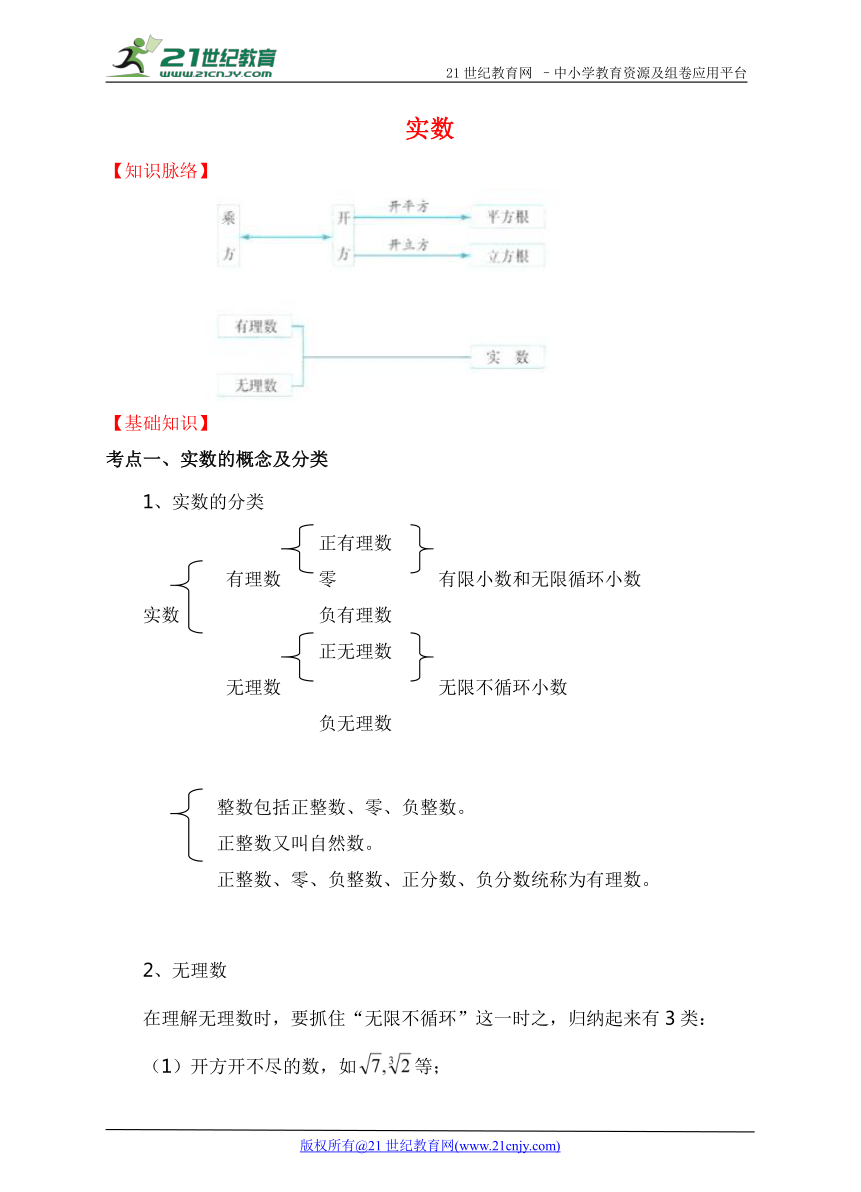
【知识脉络】
( http: / / www.21cnjy.com )
【基础知识】
考点一、实数的概念及分类
1、实数的分类
正有理数
有理数 零 有限小数和无限循环小数
实数 负有理数
正无理数
无理数 无限不循环小数
负无理数
整数包括正整数、零、负整数。
正整数又叫自然数。
正整数、零、负整数、正分数、负分数统称为有理数。
2、无理数
在理解无理数时,要抓住“无限不循环”这一时之,归纳起来有3类:
(1)开方开不尽的数,如等;
(2)有特定意义的数,如圆周率π,或化简后含有π的数,如+8等;
(3)有特定结构的数,如0.1010010001…等;
考点二、实数的倒数、相反数和绝对值
1、相反数
实数与它的相反数时一对数(只有符号不同的 ( http: / / www.21cnjy.com )两个数叫做互为相反数,零的相反数是零),从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果a与b互为相反数,则有a+b=0,a=—b,反之亦成立。21cnjy.com
2、绝对值
一个数的绝对值就是表示这个数的点与原点的距 ( http: / / www.21cnjy.com )离,|a|≥0。零的绝对值时它本身,也可看成它的相反数,若|a|=a,则a≥0;若|a|=-a,则a≤0。正数大于零,负数小于零,正数大于一切负数,两个负数,绝对值大的反而小。
3、倒数
如果a与b互为倒数,则有ab=1,反之亦成立。倒数等于本身的数是1和-1。零没有倒数。
考点三、平方根、算数平方根和立方根
1、平方根
如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟)。
一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根。
正数a的平方根记做“”。
2、算术平方根
正数a的正的平方根叫做a的算术平方根,记作“”。
正数和零的算术平方根都只有一个,零的算术平方根是零。
;注意的双重非负性:
3、立方根
如果一个数的立方等于a,那么这个数就叫做a 的立方根(或a 的三次方根)。
一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
注意:,这说明三次根号内的负号可以移到根号外面。
考点四、科学记数法和近似数
1、有效数字
一个近似数四舍五入到哪一位,就说它精确到哪一位,这时,从左边第一个不是零的数字起到右边精确的数位止的所有数字,都叫做这个数的有效数字。
2、科学记数法
把一个数写做的形式,其中,n是整数,这种记数法叫做科学记数法。
考点五、实数大小的比较
1、数轴
规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。
解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵活运用。
2、实数大小比较的几种常用方法
(1)数轴比较:在数轴上表示的两个数,右边的数总比左边的数大。
(2)求差比较:设a、b是实数,
(3)求商比较法:设a、b是两正实数,
(4)绝对值比较法:设a、b是两负实数,则。
(5)平方法:设a、b是两负实数,则。
【典例解析】
例题1:已知某正数的两个平方根分别是m+4和2m﹣16,n的立方根是﹣2,求﹣n﹣m的算术平方根.
【考点】立方根;平方根;算术平方根.
【分析】首先根据平方根的性质,求出m值,再根据立方根的性质求出n,带入﹣n﹣m,求出这个值的算术平方根即可.21教育网
【解答】解:∵某正数的两个平方根分别是m+4和2m﹣16,
可得:m+4+2m﹣16=0,
解得:m=4,
∵n的立方根是﹣2,
∴n=﹣8,
把m=4,n=﹣8代入﹣n﹣m=8﹣4=4,
所以﹣n﹣m的算术平方根是2
例题2:已知a,b,c在数轴上如图所示,化简: ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
【考点】二次根式的性质与化简;实数与数轴.
【分析】根据数轴abc的位置推出a+b<0 ( http: / / www.21cnjy.com ),c﹣a>0,b+c<0,根据二次根式的性质和绝对值进行化简得出﹣a+a+b+c﹣a﹣b﹣c,再合并即可.
【解答】解:∵从数轴可知:a<b<0<c,
∴a+b<0,c﹣a>0,b+c<0,
∴ ( http: / / www.21cnjy.com )﹣|a+b|+ ( http: / / www.21cnjy.com )+|b+c|
=﹣a+a+b+c﹣a﹣b﹣c
=﹣a.
【点评】本题考查了二次根式的性质,实数、数轴的应用,关键是能得出﹣a+a+b+c﹣a﹣b例题3:如图,数轴上表示1、 ( http: / / www.21cnjy.com )的对应点分别为点A、点B,若点A是BC的中点,则点C表示的数为 .www.21-cn-jy.com
( http: / / www.21cnjy.com )
【考点】实数与数轴.
【分析】设点C表示的数是x,再根据中点坐标公式即可得出x的值.
【解答】解:设点C表示的数是x,
∵数轴上表示1、 ( http: / / www.21cnjy.com )的对应点分别为点A、点B,点A是BC的中点,
∴ ( http: / / www.21cnjy.com )=1,解得x=2﹣ ( http: / / www.21cnjy.com ).
故选D.
【点评】本题考查的是实数与数轴,熟知数轴上的点与实数是一一对应关系是解答此题的关键.
例题4:若一个数的平方根是2a﹣3和4﹣a,求这个数.
【考点】平方根.
【分析】根据一个正数的平方根有两个,且互为相反数,可得出a的值,继而得出这个正数.
【解答】解:由题意得,2a﹣3+4﹣a=0,
解得:a=﹣1,
则2a﹣3=﹣2﹣3=﹣5,
则这个数为25.
【点评】本题考查了平方根的知识,解答本题关键是掌握一个正数的平方根有两个,且互为相反数.
【跟踪训练】
1. 在数轴上标注了四段范围,如图,则表示 ( http: / / www.21cnjy.com )的点落在( )
( http: / / www.21cnjy.com )
A.段① B.段② C.段③ D.段④
2. 阅读下面材料:点A, ( http: / / www.21cnjy.com )B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.当A,B两点中有一点在原点时:设点A在原点处,如图①,则|AB|=|OB|=|a-b|;2·1·c·n·j·y
当A,B两点都不在原点时:
如图②所示,点A,B都在原点的右边,则|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;【来源:21·世纪·教育·网】
如图③所示,点A,B都在原点的左边,则|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;21·世纪*教育网
如图④所示,点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|;21*cnjy*com
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图① 图②
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图③ 图④
回答下列问题:
(1)数轴上表示2和5两点之间的距离为 ( http: / / www.21cnjy.com )__________,数轴上表示-2和-5两点之间的距离是__________,数轴上表示1和-3的两点之间的距离是__________;
(2)数轴上表示x和-1的两点A和B之间的距离是__________,若|AB|=2,求x的值.
3. 某地开辟了一块长方形的荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2.www-2-1-cnjy-com
(1)公园的宽大约是多少?它有1 000 m吗?
(2)如果要求误差小于10 m,它的宽大约是多少?
(3)该公园中心有一圆形花坛,面积是800 m2,它的半径大约是多少米(误差小于1 m)
4. (1)已知a,b满足,解关于x的方程(a+2)x+b2=a-1.
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为,求代数式x2+(a+b)cdx+的值.【来源:21cnj*y.co*m】
参考答案;
1. 在数轴上标注了四段范围,如图,则表示 ( http: / / www.21cnjy.com )的点落在( )
( http: / / www.21cnjy.com )
A.段① B.段② C.段③ D.段④
【考点】估算无理数的大小;实数与数轴.
【分析】根据数的平方,即可解答.
【解答】解:2.62=6.76,2.72=7.29,2.82=7.84,2.92=8.41,32=9,
∵7.84<8<8.41,
∴ ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com )的点落在段③,
故选:C.
2. 阅读下面材料:点A,B在数轴 ( http: / / www.21cnjy.com )上分别表示实数a,b,A,B两点之间的距离表示为|AB|.当A,B两点中有一点在原点时:设点A在原点处,如图①,则|AB|=|OB|=|a-b|;21世纪教育网版权所有
当A,B两点都不在原点时:
如图②所示,点A,B都在原点的右边,则|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;2-1-c-n-j-y
如图③所示,点A,B都在原点的左边,则|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;【出处:21教育名师】
如图④所示,点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|;【版权所有:21教育】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图① 图②
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图③ 图④
回答下列问题:
(1)数轴上表示2和5两点之间的距 ( http: / / www.21cnjy.com )离为__________,数轴上表示-2和-5两点之间的距离是__________,数轴上表示1和-3的两点之间的距离是__________;
(2)数轴上表示x和-1的两点A和B之间的距离是__________,若|AB|=2,求x的值.
【解析】解:(1)3 3 4
(2)|AB|=|x-(-1)|=|x+1|,
当|AB|=2时,|x+1|=2,于是x+1=±2.故x=1或x=-3.
3. 某地开辟了一块长方形的荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2.21教育名师原创作品
(1)公园的宽大约是多少?它有1 000 m吗?
(2)如果要求误差小于10 m,它的宽大约是多少?
(3)该公园中心有一圆形花坛,面积是800 m2,它的半径大约是多少米(误差小于1 m)
解:(1)设公园的宽为x m,则x·2x=400 000,.
因为4002=160 000<200 000,5002=250 000>200 000,
所以400<x<500.
答:公园的宽大约有400多m,没有1 000 m宽.
(2)因为4402=193 600,4502=202 500,
所以193 600<200 000<202 500.
于是可知440<x<450.因为误差可以小于10 m,
所以公园的宽可以是440 m或450 m.
(3)设花坛的半径为R m,则πR2=800,
可得R2≈254.6.因为225<254.6<256,
所以152<R2<162.因为误差可以小于1 m,所以花坛的半径大约是15 m或16 m.
4. (1)已知a,b满足,解关于x的方程(a+2)x+b2=a-1.
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为,求代数式x2+(a+b)cdx+的值.21·cn·jy·com
解:(1)因为,|b-|≥0,而,所以有2a+8=0,b-=0,解得a=-4,.
把a=-4,代入方程(a+2)x+b2=a-1中得(-4+2)x+()2=-4-1,整理得
-2x+3=-5,x=4.
(2)因为实数a,b互为相反数,c,d互为倒数,x的绝对值为,所以a+b=0,cd=1,.
故x2+(a+b)cdx+=(±)2+0×1×(±)+0+1=7+0+0+1=8.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
实数
【知识脉络】
( http: / / www.21cnjy.com )
【基础知识】
考点一、实数的概念及分类
1、实数的分类
正有理数
有理数 零 有限小数和无限循环小数
实数 负有理数
正无理数
无理数 无限不循环小数
负无理数
整数包括正整数、零、负整数。
正整数又叫自然数。
正整数、零、负整数、正分数、负分数统称为有理数。
2、无理数
在理解无理数时,要抓住“无限不循环”这一时之,归纳起来有3类:
(1)开方开不尽的数,如等;
(2)有特定意义的数,如圆周率π,或化简后含有π的数,如+8等;
(3)有特定结构的数,如0.1010010001…等;
考点二、实数的倒数、相反数和绝对值
1、相反数
实数与它的相反数时一对数(只有符号不同的 ( http: / / www.21cnjy.com )两个数叫做互为相反数,零的相反数是零),从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果a与b互为相反数,则有a+b=0,a=—b,反之亦成立。21cnjy.com
2、绝对值
一个数的绝对值就是表示这个数的点与原点的距 ( http: / / www.21cnjy.com )离,|a|≥0。零的绝对值时它本身,也可看成它的相反数,若|a|=a,则a≥0;若|a|=-a,则a≤0。正数大于零,负数小于零,正数大于一切负数,两个负数,绝对值大的反而小。
3、倒数
如果a与b互为倒数,则有ab=1,反之亦成立。倒数等于本身的数是1和-1。零没有倒数。
考点三、平方根、算数平方根和立方根
1、平方根
如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟)。
一个数有两个平方根,他们互为相反数;零的平方根是零;负数没有平方根。
正数a的平方根记做“”。
2、算术平方根
正数a的正的平方根叫做a的算术平方根,记作“”。
正数和零的算术平方根都只有一个,零的算术平方根是零。
;注意的双重非负性:
3、立方根
如果一个数的立方等于a,那么这个数就叫做a 的立方根(或a 的三次方根)。
一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
注意:,这说明三次根号内的负号可以移到根号外面。
考点四、科学记数法和近似数
1、有效数字
一个近似数四舍五入到哪一位,就说它精确到哪一位,这时,从左边第一个不是零的数字起到右边精确的数位止的所有数字,都叫做这个数的有效数字。
2、科学记数法
把一个数写做的形式,其中,n是整数,这种记数法叫做科学记数法。
考点五、实数大小的比较
1、数轴
规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。
解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵活运用。
2、实数大小比较的几种常用方法
(1)数轴比较:在数轴上表示的两个数,右边的数总比左边的数大。
(2)求差比较:设a、b是实数,
(3)求商比较法:设a、b是两正实数,
(4)绝对值比较法:设a、b是两负实数,则。
(5)平方法:设a、b是两负实数,则。
【典例解析】
例题1:已知某正数的两个平方根分别是m+4和2m﹣16,n的立方根是﹣2,求﹣n﹣m的算术平方根.
【考点】立方根;平方根;算术平方根.
【分析】首先根据平方根的性质,求出m值,再根据立方根的性质求出n,带入﹣n﹣m,求出这个值的算术平方根即可.21教育网
【解答】解:∵某正数的两个平方根分别是m+4和2m﹣16,
可得:m+4+2m﹣16=0,
解得:m=4,
∵n的立方根是﹣2,
∴n=﹣8,
把m=4,n=﹣8代入﹣n﹣m=8﹣4=4,
所以﹣n﹣m的算术平方根是2
例题2:已知a,b,c在数轴上如图所示,化简: ( http: / / www.21cnjy.com ).
( http: / / www.21cnjy.com )
【考点】二次根式的性质与化简;实数与数轴.
【分析】根据数轴abc的位置推出a+b<0 ( http: / / www.21cnjy.com ),c﹣a>0,b+c<0,根据二次根式的性质和绝对值进行化简得出﹣a+a+b+c﹣a﹣b﹣c,再合并即可.
【解答】解:∵从数轴可知:a<b<0<c,
∴a+b<0,c﹣a>0,b+c<0,
∴ ( http: / / www.21cnjy.com )﹣|a+b|+ ( http: / / www.21cnjy.com )+|b+c|
=﹣a+a+b+c﹣a﹣b﹣c
=﹣a.
【点评】本题考查了二次根式的性质,实数、数轴的应用,关键是能得出﹣a+a+b+c﹣a﹣b例题3:如图,数轴上表示1、 ( http: / / www.21cnjy.com )的对应点分别为点A、点B,若点A是BC的中点,则点C表示的数为 .www.21-cn-jy.com
( http: / / www.21cnjy.com )
【考点】实数与数轴.
【分析】设点C表示的数是x,再根据中点坐标公式即可得出x的值.
【解答】解:设点C表示的数是x,
∵数轴上表示1、 ( http: / / www.21cnjy.com )的对应点分别为点A、点B,点A是BC的中点,
∴ ( http: / / www.21cnjy.com )=1,解得x=2﹣ ( http: / / www.21cnjy.com ).
故选D.
【点评】本题考查的是实数与数轴,熟知数轴上的点与实数是一一对应关系是解答此题的关键.
例题4:若一个数的平方根是2a﹣3和4﹣a,求这个数.
【考点】平方根.
【分析】根据一个正数的平方根有两个,且互为相反数,可得出a的值,继而得出这个正数.
【解答】解:由题意得,2a﹣3+4﹣a=0,
解得:a=﹣1,
则2a﹣3=﹣2﹣3=﹣5,
则这个数为25.
【点评】本题考查了平方根的知识,解答本题关键是掌握一个正数的平方根有两个,且互为相反数.
【跟踪训练】
1. 在数轴上标注了四段范围,如图,则表示 ( http: / / www.21cnjy.com )的点落在( )
( http: / / www.21cnjy.com )
A.段① B.段② C.段③ D.段④
2. 阅读下面材料:点A, ( http: / / www.21cnjy.com )B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.当A,B两点中有一点在原点时:设点A在原点处,如图①,则|AB|=|OB|=|a-b|;2·1·c·n·j·y
当A,B两点都不在原点时:
如图②所示,点A,B都在原点的右边,则|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;【来源:21·世纪·教育·网】
如图③所示,点A,B都在原点的左边,则|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;21·世纪*教育网
如图④所示,点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|;21*cnjy*com
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图① 图②
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图③ 图④
回答下列问题:
(1)数轴上表示2和5两点之间的距离为 ( http: / / www.21cnjy.com )__________,数轴上表示-2和-5两点之间的距离是__________,数轴上表示1和-3的两点之间的距离是__________;
(2)数轴上表示x和-1的两点A和B之间的距离是__________,若|AB|=2,求x的值.
3. 某地开辟了一块长方形的荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2.www-2-1-cnjy-com
(1)公园的宽大约是多少?它有1 000 m吗?
(2)如果要求误差小于10 m,它的宽大约是多少?
(3)该公园中心有一圆形花坛,面积是800 m2,它的半径大约是多少米(误差小于1 m)
4. (1)已知a,b满足,解关于x的方程(a+2)x+b2=a-1.
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为,求代数式x2+(a+b)cdx+的值.【来源:21cnj*y.co*m】
参考答案;
1. 在数轴上标注了四段范围,如图,则表示 ( http: / / www.21cnjy.com )的点落在( )
( http: / / www.21cnjy.com )
A.段① B.段② C.段③ D.段④
【考点】估算无理数的大小;实数与数轴.
【分析】根据数的平方,即可解答.
【解答】解:2.62=6.76,2.72=7.29,2.82=7.84,2.92=8.41,32=9,
∵7.84<8<8.41,
∴ ( http: / / www.21cnjy.com ),
∴ ( http: / / www.21cnjy.com )的点落在段③,
故选:C.
2. 阅读下面材料:点A,B在数轴 ( http: / / www.21cnjy.com )上分别表示实数a,b,A,B两点之间的距离表示为|AB|.当A,B两点中有一点在原点时:设点A在原点处,如图①,则|AB|=|OB|=|a-b|;21世纪教育网版权所有
当A,B两点都不在原点时:
如图②所示,点A,B都在原点的右边,则|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;2-1-c-n-j-y
如图③所示,点A,B都在原点的左边,则|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;【出处:21教育名师】
如图④所示,点A,B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|;【版权所有:21教育】
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图① 图②
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图③ 图④
回答下列问题:
(1)数轴上表示2和5两点之间的距 ( http: / / www.21cnjy.com )离为__________,数轴上表示-2和-5两点之间的距离是__________,数轴上表示1和-3的两点之间的距离是__________;
(2)数轴上表示x和-1的两点A和B之间的距离是__________,若|AB|=2,求x的值.
【解析】解:(1)3 3 4
(2)|AB|=|x-(-1)|=|x+1|,
当|AB|=2时,|x+1|=2,于是x+1=±2.故x=1或x=-3.
3. 某地开辟了一块长方形的荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2.21教育名师原创作品
(1)公园的宽大约是多少?它有1 000 m吗?
(2)如果要求误差小于10 m,它的宽大约是多少?
(3)该公园中心有一圆形花坛,面积是800 m2,它的半径大约是多少米(误差小于1 m)
解:(1)设公园的宽为x m,则x·2x=400 000,.
因为4002=160 000<200 000,5002=250 000>200 000,
所以400<x<500.
答:公园的宽大约有400多m,没有1 000 m宽.
(2)因为4402=193 600,4502=202 500,
所以193 600<200 000<202 500.
于是可知440<x<450.因为误差可以小于10 m,
所以公园的宽可以是440 m或450 m.
(3)设花坛的半径为R m,则πR2=800,
可得R2≈254.6.因为225<254.6<256,
所以152<R2<162.因为误差可以小于1 m,所以花坛的半径大约是15 m或16 m.
4. (1)已知a,b满足,解关于x的方程(a+2)x+b2=a-1.
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为,求代数式x2+(a+b)cdx+的值.21·cn·jy·com
解:(1)因为,|b-|≥0,而,所以有2a+8=0,b-=0,解得a=-4,.
把a=-4,代入方程(a+2)x+b2=a-1中得(-4+2)x+()2=-4-1,整理得
-2x+3=-5,x=4.
(2)因为实数a,b互为相反数,c,d互为倒数,x的绝对值为,所以a+b=0,cd=1,.
故x2+(a+b)cdx+=(±)2+0×1×(±)+0+1=7+0+0+1=8.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
