4.1.1 三角形及其内角和课件

课件54张PPT。第1课时 三角形及其
内角和第四章 三角形4.1 认识三角形1课堂讲解三角形有关概念
三角形的内角和
直角三角形两锐角互余
三角形按角的大小分类 2课时流程逐点
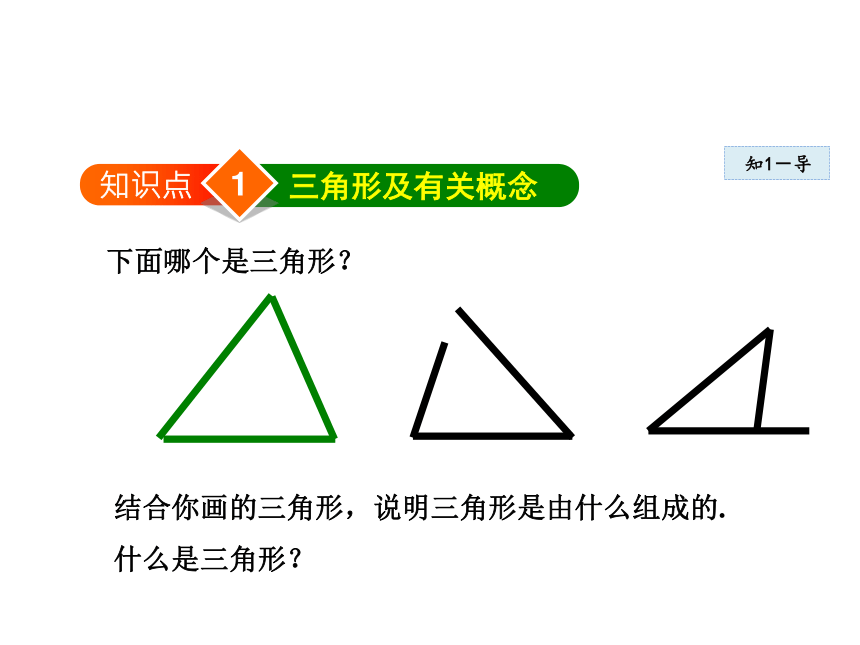
导讲练课堂小结作业提升下面请同学们仔细观察一组图片，找出你熟悉 的几何图形.你能画出一个三角形吗？知1－导1知识点三角形及有关概念下面哪个是三角形？什么是三角形？结合你画的三角形，说明三角形是由什么组成的.由不在同一条直线上的三条线段首尾顺次相接所组
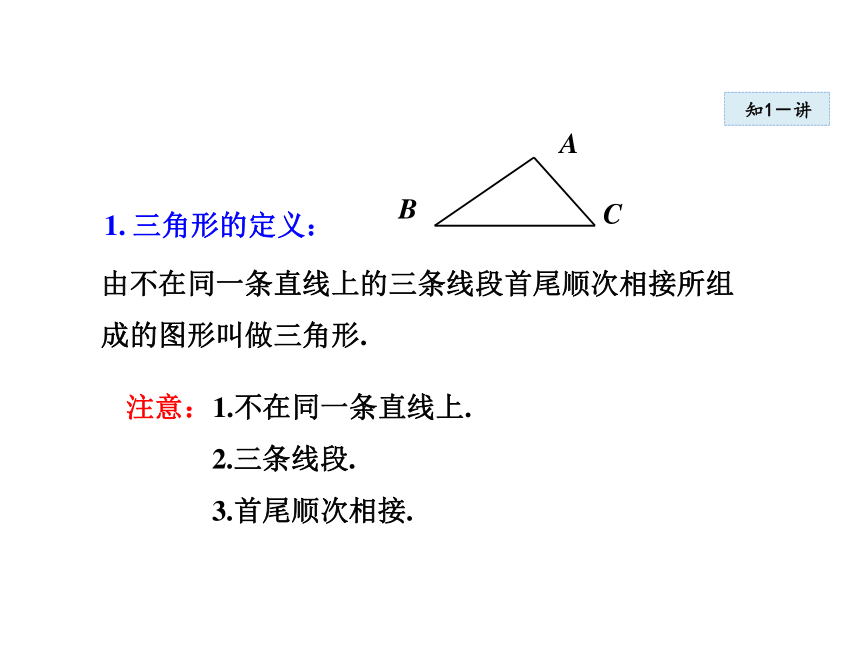
成的图形叫做三角形. 注意：1.不在同一条直线上.
2.三条线段.
3.首尾顺次相接.1. 三角形的定义：知1－讲注意：表示三角形时，字母没有先后顺序.
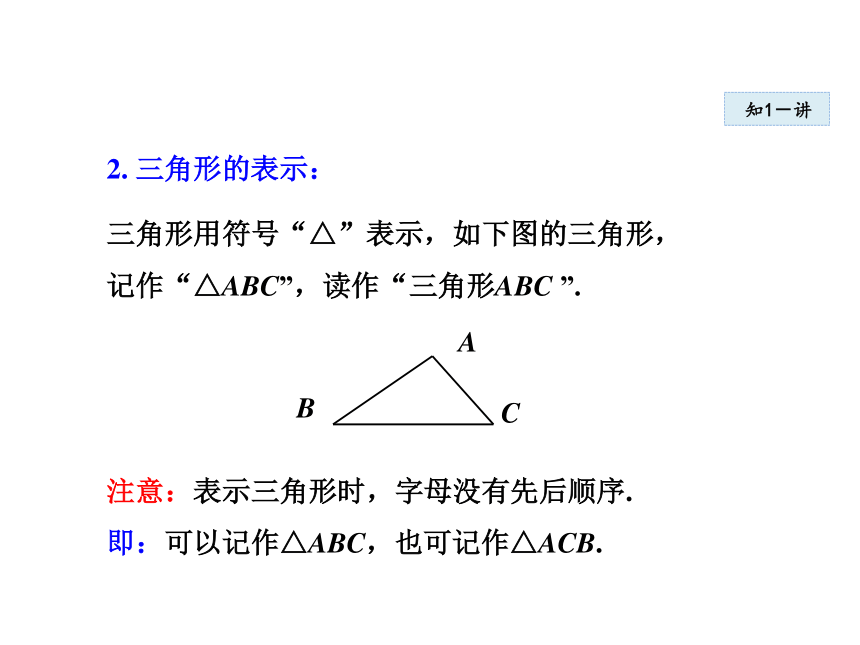
即：可以记作△ABC，也可记作△ACB.2. 三角形的表示：三角形用符号“△”表示，如下图的三角形，
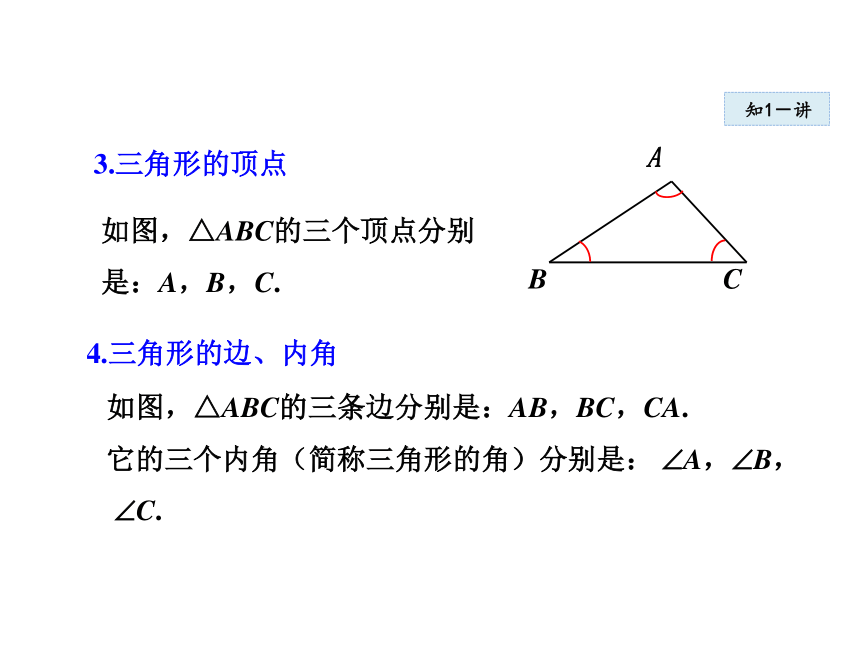
记作“△ABC”，读作“三角形ABC ”.知1－讲如图，△ABC的三个顶点分别
是：A，B，C.3.三角形的顶点如图，△ABC的三条边分别是：AB，BC，CA.
它的三个内角（简称三角形的角）分别是： ?A，?B，
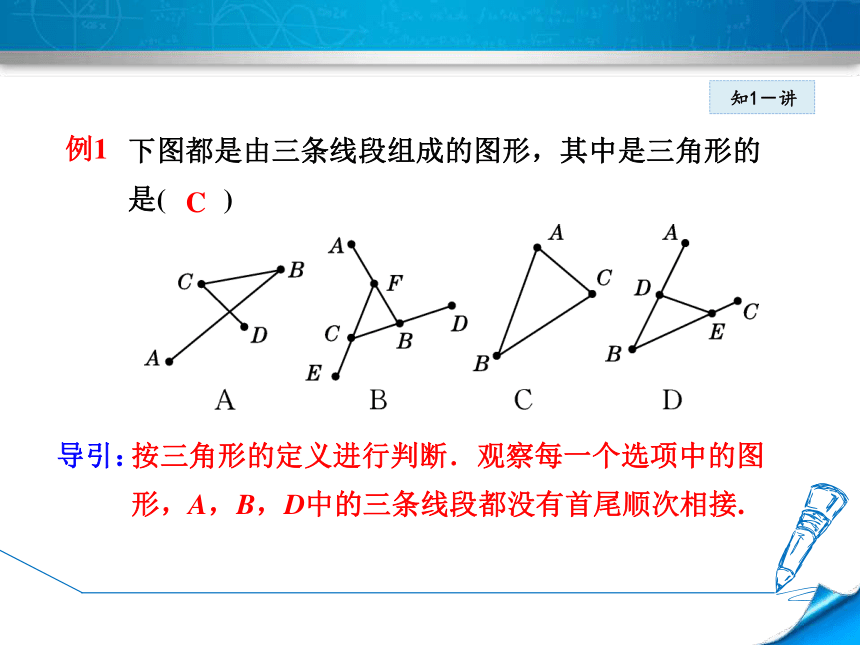
?C.ABC4.三角形的边、内角知1－讲知1－讲例1 下图都是由三条线段组成的图形，其中是三角形的
是(　　)按三角形的定义进行判断．观察每一个选项中的图
形，A，B，D中的三条线段都没有首尾顺次相接.导引：C(1)判断一个图形是否是三角形的条件：
①三条线段，②不在同一直线上，③首尾顺次相接．
三者必须同时满足，否则不是三角形．
(2)易错警示：图形是三角形与图形内含有三角形是两
个不同的概念．图形是三角形表示整个图形是一个
三角形，图形内含有三角形表示图形内局部有三角
形．如选项A，B，D中的图形内都含有三角形，但
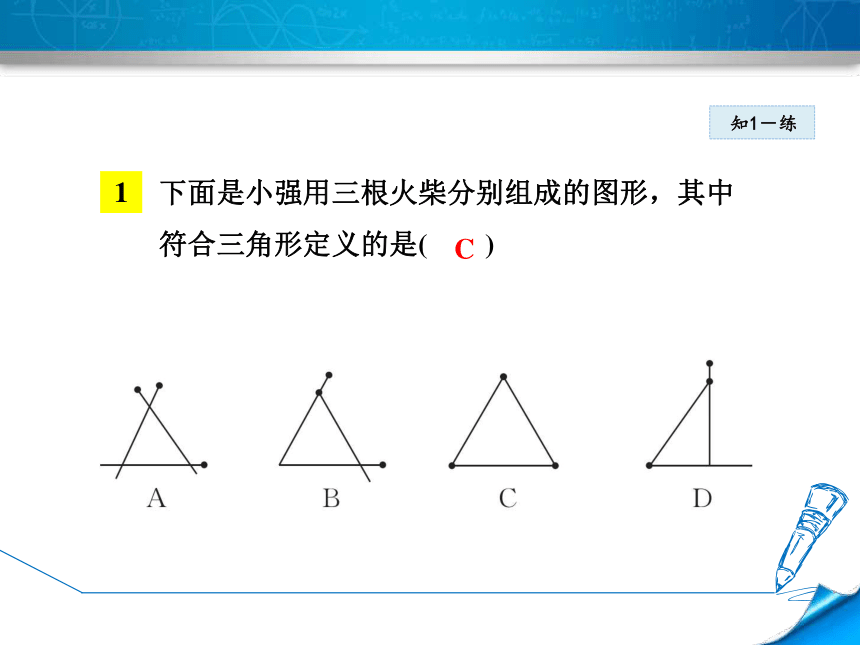
整个图形不是三角形．知1－讲1知1－练下面是小强用三根火柴分别组成的图形，其中
符合三角形定义的是(　　)C2知1－练如图，以CD为公共边的三角形是_______________；
∠EFB是________的内角；在△BCE中，BE所对
的角是________，∠CBE所对的边是__________；
以∠A为公共角的三角形_____________________
___________．△ABD，△ACE和△CDF与△BCD△BEF∠BCECE△ABC3知1－练【2016·大庆】如图①是一个三角形，分别连接这个三角形三边中点得到图②，再连接图②中间小三角形三边中点得到图③，按这样的方法进行下去，第n个图形中共有三角形的个数为________．4n－32知识点三角形的内角和 知2－导问题1　在小学我们已经知道任意一个三角形三个内
角的和等于180°，你还记得是怎么发现这个结论的
吗？请大家利用手中的三角形纸片进行探究． 方法：度量、剪拼图、折叠 知2－导知2－导知2－导 在纸上任意画一个三角形，将它的内角剪下拼合在
一起，就得到一个 平角.从这个操作过程中，你能发现
证明的思路吗？知2－导◎探究追问1　在下图中，∠B 和∠C 分别拼在∠A 的左右，
三个角合起来形成一个平角，出现了一条过点A 的直
线l，直线l 与边BC 有什么位置关系？
直线l 与边BC 平行．知2－讲追问2　在操作过程中, 我们发现了与边BC 平行的
直线l，由此，你又能受到什么启发？你能发现证明
“三角形内角和等于180°”的思路吗？
通过添加与边BC
平行的辅助线l，利用
平行线的性质和平角
的定义即可证明结论．知2－讲追问3　结合下图，你能写出已知、求证和证明吗？已知：△ABC . 求证:∠A+∠B+∠C=180°.知2－讲 如图, 过点A作直线l,使l //BC. ∵ l//BC,
∴ ∠2= ∠4 (两直线平行，内错角相等).
同理 ∠3= ∠5.
∵ ∠1 ,∠4, ∠ 5组成平角，
∴ ∠1 + ∠4+ ∠5=180° (平角定义).
∴ ∠1 + ∠2+ ∠3=180° (等量代换).
以上我们就证明了任意一个三角形的内角和都等于180°,
得到如下定理：三角形内角和定理三角形三个内角
的和等于180°.证明：知2－讲 三角形三个内角的和等于180°.知2－讲知2－讲例2 〈邵阳〉如图，在△ABC中，∠B＝46°，∠C＝54°，
AD平分∠BAC，交BC于点D，DE∥AB，交AC于点
E，则∠ADE的大小是(　　)
A．45°　　　
B．54°　　　
C．40°　　　
D．50°C知2－讲根据三角形的内角和求出∠BAC的度数，再根据角
平分线的定义求出∠BAD的度数，然后根据两直线
平行，内错角相等可得∠ADE＝∠BAD.
因为∠B＝46°，∠C＝54°，
所以∠BAC＝180°－∠B－∠C＝80°.
因为AD平分∠BAC，
所以∠BAD＝ ∠BAC＝ ×80°＝40°.
因为DE∥AB，
所以∠ADE＝∠BAD＝40°.导引： 本题运用了综合法和转化思想，借平行线将要求
的∠ADE转化成与△ABC的内角有关的∠BAD，再结
合角平分线和三角形的内角和就可以解决问题．知2－讲1【2017·南宁】如图，在△ABC中，∠A＝60°，
∠B＝40°，则∠C等于(　　)
A．100°
B．80°
C．60°
D．40°知2－练B2【2017·大庆】在△ABC中，∠A，∠B，∠C
的度数之比为2：3：4，则∠B的度数为(　　)
A．120° B．80°
C．60° D．40°知2－练C3【2017·长春】如图，在△ABC中，点D在AB
上，点E在AC上，DE∥BC. 若∠A＝62°，
∠AED＝54°，则∠B的大小为(　　)
A．54°
B．62°
C．64°
D．74°知2－练C3知识点直角三角形两锐角互余知3－讲直角三角形：
(1)定义：有一个内角是直角的三角形叫直角三角形．
表示法：直角三角形用符号“Rt△”表示，直角
三角形ABC可以写成Rt△ABC.
(2)性质：直角三角形的两个锐角互余．
如图，在Rt△ABC中，∠A＋∠B＝90°.
(3)判定：有两个角互余的三角形是直角三角形．
注意：这两个角要在同一个三角形中．知3－讲例3 如图，在△ABC中，∠A＝30°，∠B＝70°，CE
平分∠ACB，CD⊥AB于点D，DF⊥CE于点F.
(1)试说明∠BCD＝∠ECD；
(2)请找出图中所有与∠B相等的角．知3－讲(1)根据直角三角形的两个锐角互余求出∠BCD的度
数，再利用三角形的内角和求出∠ACB的度数，
然后根据角平分线的定义求出∠BCE的度数，从
而可以求出∠ECD的度数，进而得到结论；
(2)根据三角形的角度关系，找出度数是70°的角即
可．导引：知3－讲(1)因为∠B＝70°，CD⊥AB于点D，
所以∠BCD＝90°－70°＝20°.
在△ABC中，因为∠A＝30°，∠B＝70°，
所以∠ACB＝180°－30°－70°＝80°.
因为CE平分∠ACB，
所以∠BCE＝ ∠ACB＝40°.
所以∠ECD＝∠BCE－∠BCD
＝40°－20°＝20°.
所以∠BCD＝∠ECD.解：知3－讲(2)因为CD⊥AB于点D，DF⊥CE于点F，
所以∠CED＝90°－∠ECD
＝90°－20°＝70°，
∠CDF＝90°－∠ECD
＝90°－20°＝70°，
所以与∠B相等的角有∠CED和∠CDF. 直角三角形是特殊的三角形，直角三角形的两
个锐角互余的本质是三角形的三个内角和等于180°，
是三角形的三个内角和等于180°的一种简化应用，
利用这一性质，在直角三角形中已知一锐角可求另
一锐角．知3－讲1如图，在Rt△ABC中，∠BAC＝90°，
AD⊥BC于D. 则图中与∠B互余的角有(　　)
A．1个
B．2个
C．3个
D．4个知3－练B2　【2016·苏州】如图，直线a∥b，直线l与a，b分别相交于A，B两点，过点A作直线l的垂线交直线b于点C，若∠1＝58°，则∠2的度数为(　　)
A．58°
B．42°
C．32°
D．28°知3－练C3　【中考·襄阳】如图，将一块含有30°角的直角三角尺的两个顶点放在长方形直尺的一组对边上，如果∠2＝60°，那么∠1的度数为(　　)
A．60°
B．50°
C．40°
D．30°知3－练D4知识点三角形按角的大小分类 知4－导议一议
(1)下图中小明所拿三角形被遮住的两个内角是什么角？
小颖的呢? 试着说明理由.知4－导(2)下图中三角形被遮住的两个内角可能是什么角？
将所得结果与(1)的结果进行比较. 我们可以按三角形内角的大小把三角形分为三类：知4－导知4－讲 任何一个三角形中，至少有两个锐角，最多有
一个钝角或直角，因此三角形按角分类如下：知4－讲例4 〈滨州〉在△ABC中，∠A∶∠B∶∠C＝1∶2∶3，试判断△ABC的形状，并说明理由．引用辅助量x°，用x°表示出△ABC的三个内角，
然后在△ABC中，运用三角形的内角和构造方程，
解方程后，求出△ABC中各内角的度数，从而判断
△ABC的形状．导引：知4－讲△ABC是直角三角形．理由如下：
因为∠A∶∠B∶∠C＝1∶2∶3，
所以可设∠A，∠B，∠C的度数分别为x°，2x°，
3x°.
在△ABC中，因为∠A＋∠B＋∠C＝180°，
所以x°＋2x°＋3x°＝180°，解得x°＝30°.
所以∠A＝30°，∠B＝60°，∠C＝90°.
所以△ABC是直角三角形．解：判断一个三角形的形状的方法：
(1)看三角形中最大角的大小：最大角是锐角，三角形就
是锐角三角形；最大角是直角，三角形就是直角三角
形；最大角是钝角，三角形就是钝角三角形．
(2)通过角的比例关系判断：两较小角的比例和小于最大
角的比例，则此三角形为钝角三角形；两较小角的比
例和等于最大角的比例(两锐角互余)，则此三角形为直
角三角形；两较小角的比例和大于最大角的比例，则
此三角形为锐角三角形．知4－讲1知4－练观察下面的三角形，并把它们的标号填入相应的圈内.解：锐角三角形：③⑤；
直角三角形：①④⑥；
钝角三角形：②⑦.2知4－练一个三角形两个内角的度数分别如下，这个三角形是什么三角形?
30°和 60°；(2) 40° 和 70°；
(3) 50°和 20°.解：(1)直角三角形．
(2)锐角三角形．
(3)钝角三角形．　3【2017·长沙】一个三角形的三个内角的度数之
比为1：2：3，则这个三角形一定是(　　)
A．锐角三角形
B．直角三角形
C．钝角三角形
D．等腰直角三角形知4－练B4　如图所示的三角形被木板遮住了一部分，这个三角形是(　　)
A．锐角三角形
B．直角三角形
C．钝角三角形
D．以上都有可能知4－练D1. 理解三角形定义必须明确“三点”：
(1)三条线段必须满足“不在同一条直线上”才能组成
三角形．
(2)特别要注意“首尾顺次相接”，如果三条线段不是
首尾顺次相接，那么形成的图形一定不是三角形．
(3)“△ABC”也可以写成“△ACB”“△BCA”等，就是说
三角形的三个顶点的字母的次序可以任意调换，不
过通常按26个英文字母的顺序排列．2.三角形的内角和是180°.
这是在三角形内部求角的度数的重要依据.
3.三角形按角进行分类：2易错小结根据下列条件，判断△ABC的形状．
(1)∠A＝40°，∠B＝80°；
(2)∠A∶∠B∶∠C＝2∶3∶7.易错点：判断三角形种类时，不按最大角进行判断解：(1)∠C＝180°－∠A－∠B＝60°，因为40°<60°
<80°<90°，所以△ABC是锐角三角形．
(2)设∠A＝2x，∠B＝3x，∠C＝7x，
则2x＋3x＋7x＝180°，解得x＝15°.
所以∠C＝7×15°＝105°.
所以△ABC是钝角三角形．