人教版八年级数学专题讲解第05讲:分式的化简与求值
文档属性
| 名称 | 人教版八年级数学专题讲解第05讲:分式的化简与求值 |  | |
| 格式 | doc | ||
| 文件大小 | 397.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-08 17:51:26 | ||
图片预览




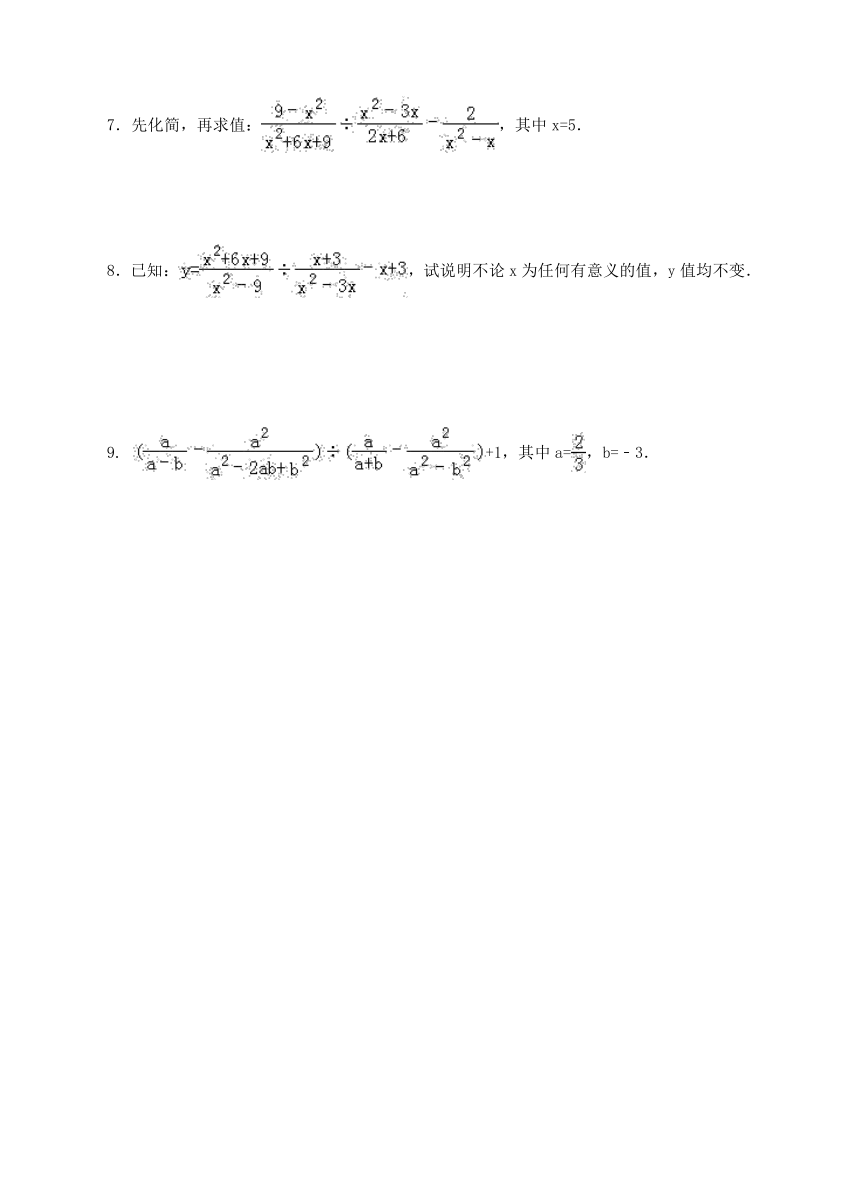
文档简介
专题05 分式的化简与求值
阅读与思考
给出一定的条件,在此条件下求分式的值称为 ( http: / / www.21cnjy.com )有条件的分式求值.而分式的化简与求值是紧密相连的,求值之前必须先化简,化简的目的是为了求值,先化简后求值是解有条件的分式的化简与求值的基本策略.21教育网
解有条件的分式化简与求值问题时,既 ( http: / / www.21cnjy.com )要瞄准目标.又要抓住条件,既要根据目标变换条件.又要依据条件来调整目标,除了要用到整式化简求值的知识方法外,还常常用到如下技巧:21cnjy.com
1.恰当引入参数;
2.取倒数或利用倒数关系;
3.拆项变形或拆分变形;
4.整体代入;
5.利用比例性质等.
例题与求解
【例l】化简:的结果是( )
A.2 B. C. D.
【考点】分式的混合运算.
【分析】先把括号中的第二个分式约分,再利用乘法分配律把(x﹣3)分别与括号中的式子相乘可使计算简便.21·cn·jy·com
【解答】解:
=(﹣) (x﹣3)
= (x﹣3)﹣ (x﹣3)
=1﹣
=.
故选B.
【点评】归纳提炼:对于一般的分式混合运算来 ( http: / / www.21cnjy.com )讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.www.21-cn-jy.com
【例2】化简,可得( )
A. B. C. D.
【考点】分式的加减法.
【分析】先通分,然后进行同分母分式加减运算,最后要注意将结果化为最简分式.
【解答】解: ==.
故选B.
【点评】本题考查了分式的加减运算,题目比较容易.
【例3】已知x=2012,y=2013,则(x+y) = .
【考点】分式的化简求值.
【分析】先根据分式混合运算的法则把原式进行化简,再把x、y的值代入进行计算即可.
【解答】解:原式=(x+y)
=,
当x=2012,y=2013时,原式==﹣1.
故答案为:﹣1.
【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
【例4】观察下列各等式:,,,…根据你发现的规律,计算: = (n为正整数).
【考点】分式的加减法.
【专题】压轴题;规律型.
【分析】本题重在理解规律,从规律中我们可以发现,中间的数值都是相反数,所以最后的结果就是,化简即可.2·1·c·n·j·y
【解答】解:原式=2(1﹣)+2(﹣)+2(﹣)…+2(﹣)=2(1﹣)=.故答案为.【来源:21·世纪·教育·网】
【点评】本题主要是利用规律求值,能够理解本题中给出的规律是解答本题的关键.
【例5】.化简: +.
【考点】分式的混合运算.
【分析】根据分式混合运算的法则进行计算即可.
【解答】解:原式=+
=+
=
=.
【点评】本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.
【例6】已知,则的y2+4y+x值为 .
【考点】分式的化简求值.
【分析】此题可先从下手,通过变形可得,再变形即可求得结果.
【解答】解:由于,则通过变形可得:,
即,∴y2+4y+x=2.
【点评】本题考查了分式的化简求值,关键是从题中所给的等式下手,找到切入点.
能力训练
1.化简: = .
2.已知非零有理数x,y满足x2﹣6xy+9y2=0,则=( )
A. B. C. D.
3. 若的值是 .
4.化简:.
5.已知x﹣3y=0,求 (x﹣y)的值.
7.先化简,再求值:,其中x=5.
8.已知:,试说明不论x为任何有意义的值,y值均不变.
9. +1,其中a=,b=﹣3.
参考答案:
1.化简: = x+y .
【考点】分式的加减法.
【专题】计算题.
【分析】同分母相减,分母不变,分子相减,要利用平方差公式化为最简分式.
【解答】解: ==x+y.
【点评】本题考查了分式的加减法法则.
2.已知非零有理数x,y满足x2﹣6xy+9y2=0,则=( )
A. B. C. D.
【考点】分式的值.
【分析】由x2﹣6xy+9y2=0,根据完全平方公式得出x=3y,再代入,计算即可求出其值.
【解答】解:∵x2﹣6xy+9y2=0,
∴(x﹣3y)2=0,
∴x=3y,
∴==.
故选C.
【点评】本题考查了完全平方公式及分式的值,由完全平方公式得出x=3y是解题的关键.
3. 若的值是 11 .
【考点】完全平方公式.
【专题】计算题.
【分析】把x﹣=3利用完全平方公式两边平方展开,整理即可得解.
【解答】解:∵x﹣=3,
∴(x﹣)2=9,
即x2﹣2+=9,
解得x2+=9+2=11.
故答案为:11.
【点评】本题主要考查了完全平方公式的运用,利用好乘积二倍项不含字母是解题的关键.
4.)化简:.
【考点】分式的混合运算.
【分析】根据分式混合运算的法则进行计算即可.
【解答】解:原式= ﹣
=﹣
=0.
【点评】本题考查的是分式的混合运算,在解答此类题目时要注意通分及约分的灵活应用.
5.已知x﹣3y=0,求 (x﹣y)的值.
【考点】分式的化简求值.
【专题】计算题.
【分析】首先将分式的分母分解因式,然后再约分、化简,最后将x、y的关系式代入化简后的式子中进行计算即可.21世纪教育网版权所有
【解答】解: =(2分)
=;
当x﹣3y=0时,x=3y;
原式=.(8分)
【点评】分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.
7.先化简,再求值:,其中x=5.
【考点】分式的化简求值.
【分析】先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
【解答】解:原式= ﹣
=﹣﹣
=﹣
=﹣
=,
当x=5时,原式==﹣.
【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
8.已知:,试说明不论x为任何有意义的值,y值均不变.
【考点】分式的混合运算.
【专题】证明题.
【分析】先把分子分母分解因式再化简约分即可.
【解答】证明:
=
=x﹣x+3
=3.
故不论x为任何有意义的值,y值均不变.
【点评】本题主要考查了分式的混合运算能力
9. +1,其中a=,b=﹣3.
【考点】分式的化简求值.
【专题】计算题.
【分析】此题的运算顺序:先括号里,经过通分,再把除法转化为乘法,约分化为最简,最后代值计算.
【解答】解:原式=+1
=+1;
当a=,b=﹣3时,原式=.
【点评】本题主要考查分式的化简求值,通分、约分是解答的关键.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
阅读与思考
给出一定的条件,在此条件下求分式的值称为 ( http: / / www.21cnjy.com )有条件的分式求值.而分式的化简与求值是紧密相连的,求值之前必须先化简,化简的目的是为了求值,先化简后求值是解有条件的分式的化简与求值的基本策略.21教育网
解有条件的分式化简与求值问题时,既 ( http: / / www.21cnjy.com )要瞄准目标.又要抓住条件,既要根据目标变换条件.又要依据条件来调整目标,除了要用到整式化简求值的知识方法外,还常常用到如下技巧:21cnjy.com
1.恰当引入参数;
2.取倒数或利用倒数关系;
3.拆项变形或拆分变形;
4.整体代入;
5.利用比例性质等.
例题与求解
【例l】化简:的结果是( )
A.2 B. C. D.
【考点】分式的混合运算.
【分析】先把括号中的第二个分式约分,再利用乘法分配律把(x﹣3)分别与括号中的式子相乘可使计算简便.21·cn·jy·com
【解答】解:
=(﹣) (x﹣3)
= (x﹣3)﹣ (x﹣3)
=1﹣
=.
故选B.
【点评】归纳提炼:对于一般的分式混合运算来 ( http: / / www.21cnjy.com )讲,其运算顺序与整式混合运算一样,是先乘方,再乘除,最后算加减,如果遇括号要先算括号里面的.在此基础上,有时也应该根据具体问题的特点,灵活应变,注意方法.www.21-cn-jy.com
【例2】化简,可得( )
A. B. C. D.
【考点】分式的加减法.
【分析】先通分,然后进行同分母分式加减运算,最后要注意将结果化为最简分式.
【解答】解: ==.
故选B.
【点评】本题考查了分式的加减运算,题目比较容易.
【例3】已知x=2012,y=2013,则(x+y) = .
【考点】分式的化简求值.
【分析】先根据分式混合运算的法则把原式进行化简,再把x、y的值代入进行计算即可.
【解答】解:原式=(x+y)
=,
当x=2012,y=2013时,原式==﹣1.
故答案为:﹣1.
【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
【例4】观察下列各等式:,,,…根据你发现的规律,计算: = (n为正整数).
【考点】分式的加减法.
【专题】压轴题;规律型.
【分析】本题重在理解规律,从规律中我们可以发现,中间的数值都是相反数,所以最后的结果就是,化简即可.2·1·c·n·j·y
【解答】解:原式=2(1﹣)+2(﹣)+2(﹣)…+2(﹣)=2(1﹣)=.故答案为.【来源:21·世纪·教育·网】
【点评】本题主要是利用规律求值,能够理解本题中给出的规律是解答本题的关键.
【例5】.化简: +.
【考点】分式的混合运算.
【分析】根据分式混合运算的法则进行计算即可.
【解答】解:原式=+
=+
=
=.
【点评】本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.
【例6】已知,则的y2+4y+x值为 .
【考点】分式的化简求值.
【分析】此题可先从下手,通过变形可得,再变形即可求得结果.
【解答】解:由于,则通过变形可得:,
即,∴y2+4y+x=2.
【点评】本题考查了分式的化简求值,关键是从题中所给的等式下手,找到切入点.
能力训练
1.化简: = .
2.已知非零有理数x,y满足x2﹣6xy+9y2=0,则=( )
A. B. C. D.
3. 若的值是 .
4.化简:.
5.已知x﹣3y=0,求 (x﹣y)的值.
7.先化简,再求值:,其中x=5.
8.已知:,试说明不论x为任何有意义的值,y值均不变.
9. +1,其中a=,b=﹣3.
参考答案:
1.化简: = x+y .
【考点】分式的加减法.
【专题】计算题.
【分析】同分母相减,分母不变,分子相减,要利用平方差公式化为最简分式.
【解答】解: ==x+y.
【点评】本题考查了分式的加减法法则.
2.已知非零有理数x,y满足x2﹣6xy+9y2=0,则=( )
A. B. C. D.
【考点】分式的值.
【分析】由x2﹣6xy+9y2=0,根据完全平方公式得出x=3y,再代入,计算即可求出其值.
【解答】解:∵x2﹣6xy+9y2=0,
∴(x﹣3y)2=0,
∴x=3y,
∴==.
故选C.
【点评】本题考查了完全平方公式及分式的值,由完全平方公式得出x=3y是解题的关键.
3. 若的值是 11 .
【考点】完全平方公式.
【专题】计算题.
【分析】把x﹣=3利用完全平方公式两边平方展开,整理即可得解.
【解答】解:∵x﹣=3,
∴(x﹣)2=9,
即x2﹣2+=9,
解得x2+=9+2=11.
故答案为:11.
【点评】本题主要考查了完全平方公式的运用,利用好乘积二倍项不含字母是解题的关键.
4.)化简:.
【考点】分式的混合运算.
【分析】根据分式混合运算的法则进行计算即可.
【解答】解:原式= ﹣
=﹣
=0.
【点评】本题考查的是分式的混合运算,在解答此类题目时要注意通分及约分的灵活应用.
5.已知x﹣3y=0,求 (x﹣y)的值.
【考点】分式的化简求值.
【专题】计算题.
【分析】首先将分式的分母分解因式,然后再约分、化简,最后将x、y的关系式代入化简后的式子中进行计算即可.21世纪教育网版权所有
【解答】解: =(2分)
=;
当x﹣3y=0时,x=3y;
原式=.(8分)
【点评】分式混合运算要注意先去括号;分子、分母能因式分解的先因式分解;除法要统一为乘法运算.
7.先化简,再求值:,其中x=5.
【考点】分式的化简求值.
【分析】先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
【解答】解:原式= ﹣
=﹣﹣
=﹣
=﹣
=,
当x=5时,原式==﹣.
【点评】本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.
8.已知:,试说明不论x为任何有意义的值,y值均不变.
【考点】分式的混合运算.
【专题】证明题.
【分析】先把分子分母分解因式再化简约分即可.
【解答】证明:
=
=x﹣x+3
=3.
故不论x为任何有意义的值,y值均不变.
【点评】本题主要考查了分式的混合运算能力
9. +1,其中a=,b=﹣3.
【考点】分式的化简求值.
【专题】计算题.
【分析】此题的运算顺序:先括号里,经过通分,再把除法转化为乘法,约分化为最简,最后代值计算.
【解答】解:原式=+1
=+1;
当a=,b=﹣3时,原式=.
【点评】本题主要考查分式的化简求值,通分、约分是解答的关键.
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
