【备考2018】中考数学一轮复习学案(江苏专用)第2节 整式运算
文档属性
| 名称 | 【备考2018】中考数学一轮复习学案(江苏专用)第2节 整式运算 |  | |
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-08 22:28:28 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第一章 数与式
第2节 整式运算
【学习目标】
了解代数式、整式的有关概念,在现实情境中 ( http: / / www.21cnjy.com )进一步理解用字母表示数的意义;能分析简单的数量关系,并用代数式表示;能解释一些简单代数式的实际背景或几何意义,会求代数式的值;了解整式指数幂的基本性质,会进行简单的整式加、减、乘、除运算(其中多项式相乘仅指一次式相乘);会推导乘法公式(平方差和完全平方公式),了解公式的几何背景,并能进行简单的计算.21·cn·jy·com
【课前热身】
1.(2017山西)某商店经销一种品牌的洗 ( http: / / www.21cnjy.com )衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为 元.www.21-cn-jy.com
( http: / / www.21cnjy.com / )
2.(2017镇江)计算: .
3.(2017连云港)计算: .
4.(2017济宁)若单项式与单项式是同类项,则的值是( )
A.2 B.3 C.4 D.5
5.(2017咸宁)由于受H7N9禽流感的影响,我市某城区今年2月份鸡的价格比1月份下降%,3月份比2月份下降%,已知1月份鸡的价格为24元/千克,设3月份鸡的价格为元/千克,则( )2·1·c·n·j·y
A.%% B.%%
C.%% D.%%
6.(2017南京)计算的结果是( )
A. B. C. D.
7.(2017重庆B)计算:.
8.(2017宁波)先化简,再求值:,其中.
【课堂互动】
知识点1 列代数式
例1 (2017吉林)苹果原价是每千克x元,按8折优惠出售,该苹果现价是每千克 元(用含x的代数式表示).【来源:21·世纪·教育·网】
例2 (2017长春)如图,将边长为3a的 ( http: / / www.21cnjy.com )正方形沿虚线剪成两块正方形和两块长方形,若拿掉边长为2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
A. B. C. D.
( http: / / www.21cnjy.com / )
跟踪训练
1.(2017杭州)某水果 ( http: / / www.21cnjy.com )店销售50千克香蕉,第一天售价为9元/千克,第二天降价为6元/千克,第三天再降为3元/千克.三天全部售完,共计所得270元.若该店第二天销售香蕉t千克,则第三天销售香蕉 千克.(用含t的代数式表示)21·世纪*教育网
2.(2017衢州)如图,从边长为的正方形纸片中剪去一个边长为3的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠无缝隙),则拼成的长方形的另一边的长是 .www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
知识点2 探寻变化规律
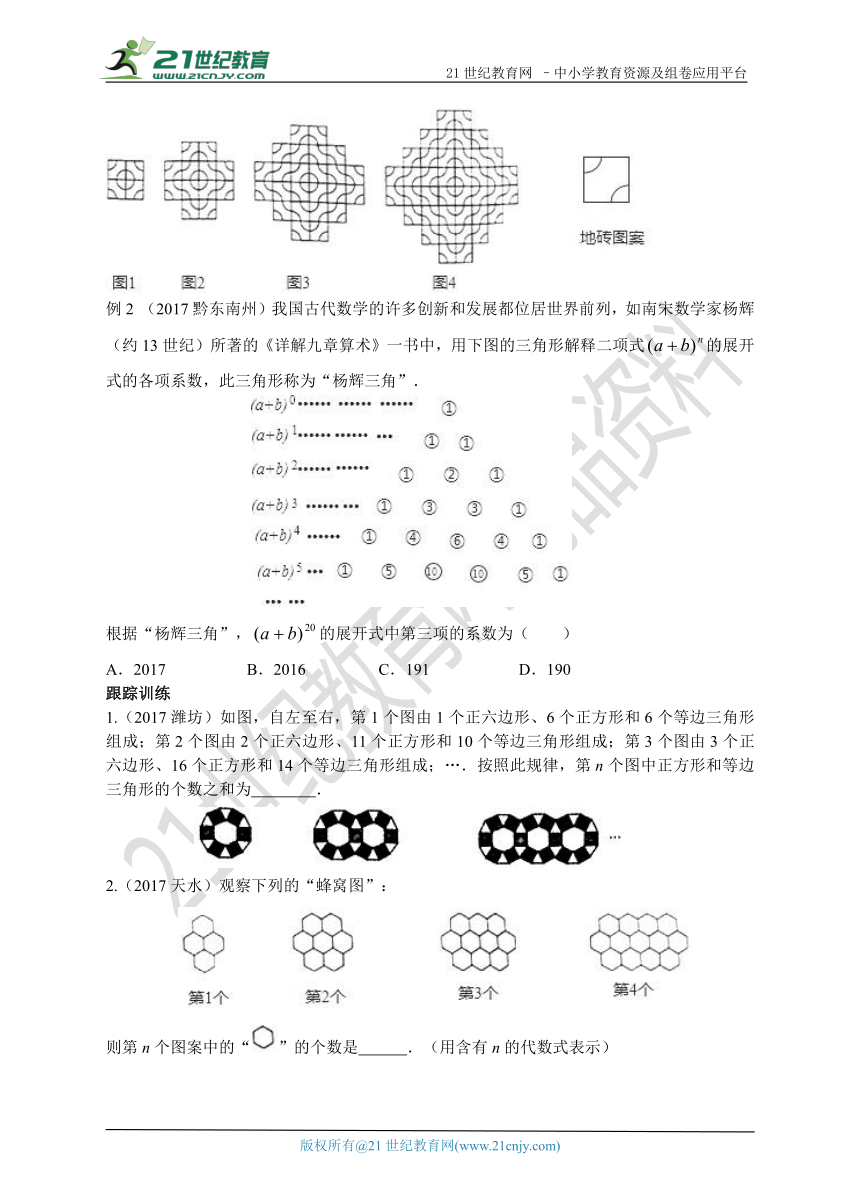
例1 (2017威海)某广场用同一种如 ( http: / / www.21cnjy.com )下图所示的地砖拼图案,第1次拼成如图1所示的图案,第2次拼成如图2所示的图案,第3次拼成如图3所示的图案,第4次拼成如图4所示的图案,….按照这样的规律进行下去,第n次拼成的图案共用地砖 块.
( http: / / www.21cnjy.com / )
例2 (2017黔东南州)我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用下图的三角形解释二项式的展开式的各项系数,此三角形称为“杨辉三角”.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
根据“杨辉三角”,的展开式中第三项的系数为( )
A.2017 B.2016 C.191 D.19021*cnjy*com
跟踪训练
1.(2017潍坊)如图,自左至右 ( http: / / www.21cnjy.com ),第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;….按照此规律,第n个图中正方形和等边三角形的个数之和为 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
2.(2017天水)观察下列的“蜂窝图”:
( http: / / www.21cnjy.com / )
则第n个图案中的“ ( http: / / www.21cnjy.com / )”的个数是 .(用含有n的代数式表示)
知识点3 整式的有关概念
例1 对于多项式,下列说法错误的是( )
A.这是一个二次三项式 B.二次项系数是1
C.一次项系数是3 D.常数项是2
例2 (2017凉山)若与是同类项,则 .
跟踪训练
1.已知一个单项式的系数是2,次数是3,则这个单项式可以是( )
A. B. C. D.
2.(2017玉林)若与是同类项,则 .
3.已知多项式是二次三项式,为常数,则的值为 .
知识点4 整式的有关运算
例1 设有理数在数轴上对应的位置如图所示,化简的结果是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
例2 (2017海南)计算:.
跟踪训练
1.(2017青岛)计算的结果为( )
A. B. C. D.
2.(2017淮安)计算: .
知识点5 求代数式的值
例1 (2017荆门)先化简,再求值:,其中.
例2 (2017娄底)先化简,再求值:,其中,是一元二次方程的两个实数根.
跟踪训练
1.(2017长春)先化简,再求值:,其中.
2.(2017门头沟区二模)已知,求代数式的值.
知识点6 说理题
例 (2017河北)发现 任意五个连续整数的平方和是的倍数.
验证 (1)的结果是的几倍?
(2)设五个连续整数的中间一个为,写出它们的平方和并说明其是的倍数.
延伸 任意三个连续整数的平方和被除的余数是几呢?请写出理由.
跟踪训练
1.(2017贵阳)下面是小颖化简整式的过程,仔细阅读后解答所提出的问题.
解:
第一步
第二步
(1)小颖的化简过程从第 步开始出现错误;
(2)对此整式进行化简.
【课后作业】
1.下列式子:,,,,,0中,整式有( )
A.3个 B.4个 C.5个 D.6个
2.(2017泰州)下列运算正确的是( )
A. B. C. D.
3.(2017孝感)下列计算正确的是( )
A. B.
C. D.
4.用大小相等的小正方形按一定规律拼成下列图形,则第个图形中小正方形的个数是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
5.某种商品的进价为a元/件,在销 ( http: / / www.21cnjy.com )售旺季,商品售价较进价高30%;销售旺季过后,商品又以7折(即原售价的70%)的价格开展促销活动,这时一件该商品的售价为( )
A.a元 B.0.7a元 C.0.91a元 D.1.03a元
6.当时,代数式的值是( )
A. B. C. D.
7.已知,,求的值.我们可以用边长分别为x和y的两种正方形组成一个图形来解决这个问题,其中,能较为简单地解决这个问题的图形是( )
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
A B C D
8.若,则的值为( )
A. B. C. D.
9.(2017烟台)用棋子摆出下列一组图形:
( http: / / www.21cnjy.com / )
按照这种规律摆下去,第个图形用的棋子个数为 .
10.计算: .
11.三个连续整数中,是最大的一个,这三个数的和为 .
12.(2017泰州)已知,则代数式的值为 .
13.按一定规律排列的一列数:,,,,,,…,若,,表示这列数中的连续三个数,猜测,,满足的关系式是 .21世纪教育网版权所有
14.(2017安顺)若代数式是一个完全平方式,则 .
15.根据如图所示的程序计算,若输入x的值为1,则输出y的值为 .
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
第15题图 第16题图
16.若一个大正方形和四个全等的小正方形按图 ( http: / / www.21cnjy.com )①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是 (用a,b的代数式表示).21教育网
17. 4个数排列成,我们称之为二项行列式.规定它的运算法则为:
.若,则 .
18.已知是方程的实根,求代数式的值.
19.先化简,再根据化简结果,你发现该代数式的值与的取值有什么关系?(不必说理)
20.选取二次三项式中的两项,配成完全平方式的过程叫配方.例如:
①选取二次项和一次项配方:;
②选取二次项和常数项配方:或
;
③选取一次项和常数项配方:.
根据上述材料,解决下面的问题:
(1)写出的两种不同形式的配方;
(2)已知,求的值.
参考答案
【课前热身】
1.1.08a 2. 3. 4.D 5.D 6.C
7.原式
8.原式,将代入,原式
【课堂互动】
知识点1 例1 0.8x 例2 A 跟踪训练 1. 2.
知识点2 例1 例2 D 跟踪训练 1. 2.
知识点3 例1 D 例2 跟踪训练 1.D 2. 3.
知识点4 例1 D 例2 原式
跟踪训练 1.C 2.
知识点5 例1 原式
当时,原式
例2 原式
因为,是一元二次方程的两个实数根
所以,则原式
跟踪训练 1.原式
当时,原式
2.原式
因为,所以原式
知识点6 例 验证:(1)因为,,
所以结果是5的3倍
(2)根据题意得:
因为,为整数,
所以它们的平方和是5的整数倍
延伸:余数为2
设任意三个连续整数中间的一个数为,则
因为……,所以余数为2
跟踪训练 1.(1)一
(2)
【课后作业】
1.B 2.C 3.B 4.C 5.C 6.B 7.B 8.B 9.
10. 11. 12. 13. 14.或 15. 16.17.21cnjy.com
18.原式,把代入方程得:,即:,则原式
19.原式,该代数式的值与的取值无关
20.(1);
(2)因为,
所以,所以,,
解得:,
所以
( http: / / www.21cnjy.com / )
…
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
第一章 数与式
第2节 整式运算
【学习目标】
了解代数式、整式的有关概念,在现实情境中 ( http: / / www.21cnjy.com )进一步理解用字母表示数的意义;能分析简单的数量关系,并用代数式表示;能解释一些简单代数式的实际背景或几何意义,会求代数式的值;了解整式指数幂的基本性质,会进行简单的整式加、减、乘、除运算(其中多项式相乘仅指一次式相乘);会推导乘法公式(平方差和完全平方公式),了解公式的几何背景,并能进行简单的计算.21·cn·jy·com
【课前热身】
1.(2017山西)某商店经销一种品牌的洗 ( http: / / www.21cnjy.com )衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为 元.www.21-cn-jy.com
( http: / / www.21cnjy.com / )
2.(2017镇江)计算: .
3.(2017连云港)计算: .
4.(2017济宁)若单项式与单项式是同类项,则的值是( )
A.2 B.3 C.4 D.5
5.(2017咸宁)由于受H7N9禽流感的影响,我市某城区今年2月份鸡的价格比1月份下降%,3月份比2月份下降%,已知1月份鸡的价格为24元/千克,设3月份鸡的价格为元/千克,则( )2·1·c·n·j·y
A.%% B.%%
C.%% D.%%
6.(2017南京)计算的结果是( )
A. B. C. D.
7.(2017重庆B)计算:.
8.(2017宁波)先化简,再求值:,其中.
【课堂互动】
知识点1 列代数式
例1 (2017吉林)苹果原价是每千克x元,按8折优惠出售,该苹果现价是每千克 元(用含x的代数式表示).【来源:21·世纪·教育·网】
例2 (2017长春)如图,将边长为3a的 ( http: / / www.21cnjy.com )正方形沿虚线剪成两块正方形和两块长方形,若拿掉边长为2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )
A. B. C. D.
( http: / / www.21cnjy.com / )
跟踪训练
1.(2017杭州)某水果 ( http: / / www.21cnjy.com )店销售50千克香蕉,第一天售价为9元/千克,第二天降价为6元/千克,第三天再降为3元/千克.三天全部售完,共计所得270元.若该店第二天销售香蕉t千克,则第三天销售香蕉 千克.(用含t的代数式表示)21·世纪*教育网
2.(2017衢州)如图,从边长为的正方形纸片中剪去一个边长为3的正方形,剩余部分沿虚线又剪拼成一个如图所示的长方形(不重叠无缝隙),则拼成的长方形的另一边的长是 .www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
知识点2 探寻变化规律
例1 (2017威海)某广场用同一种如 ( http: / / www.21cnjy.com )下图所示的地砖拼图案,第1次拼成如图1所示的图案,第2次拼成如图2所示的图案,第3次拼成如图3所示的图案,第4次拼成如图4所示的图案,….按照这样的规律进行下去,第n次拼成的图案共用地砖 块.
( http: / / www.21cnjy.com / )
例2 (2017黔东南州)我国古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用下图的三角形解释二项式的展开式的各项系数,此三角形称为“杨辉三角”.2-1-c-n-j-y
( http: / / www.21cnjy.com / )
根据“杨辉三角”,的展开式中第三项的系数为( )
A.2017 B.2016 C.191 D.19021*cnjy*com
跟踪训练
1.(2017潍坊)如图,自左至右 ( http: / / www.21cnjy.com ),第1个图由1个正六边形、6个正方形和6个等边三角形组成;第2个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成;….按照此规律,第n个图中正方形和等边三角形的个数之和为 .【来源:21cnj*y.co*m】
( http: / / www.21cnjy.com / )
2.(2017天水)观察下列的“蜂窝图”:
( http: / / www.21cnjy.com / )
则第n个图案中的“ ( http: / / www.21cnjy.com / )”的个数是 .(用含有n的代数式表示)
知识点3 整式的有关概念
例1 对于多项式,下列说法错误的是( )
A.这是一个二次三项式 B.二次项系数是1
C.一次项系数是3 D.常数项是2
例2 (2017凉山)若与是同类项,则 .
跟踪训练
1.已知一个单项式的系数是2,次数是3,则这个单项式可以是( )
A. B. C. D.
2.(2017玉林)若与是同类项,则 .
3.已知多项式是二次三项式,为常数,则的值为 .
知识点4 整式的有关运算
例1 设有理数在数轴上对应的位置如图所示,化简的结果是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
例2 (2017海南)计算:.
跟踪训练
1.(2017青岛)计算的结果为( )
A. B. C. D.
2.(2017淮安)计算: .
知识点5 求代数式的值
例1 (2017荆门)先化简,再求值:,其中.
例2 (2017娄底)先化简,再求值:,其中,是一元二次方程的两个实数根.
跟踪训练
1.(2017长春)先化简,再求值:,其中.
2.(2017门头沟区二模)已知,求代数式的值.
知识点6 说理题
例 (2017河北)发现 任意五个连续整数的平方和是的倍数.
验证 (1)的结果是的几倍?
(2)设五个连续整数的中间一个为,写出它们的平方和并说明其是的倍数.
延伸 任意三个连续整数的平方和被除的余数是几呢?请写出理由.
跟踪训练
1.(2017贵阳)下面是小颖化简整式的过程,仔细阅读后解答所提出的问题.
解:
第一步
第二步
(1)小颖的化简过程从第 步开始出现错误;
(2)对此整式进行化简.
【课后作业】
1.下列式子:,,,,,0中,整式有( )
A.3个 B.4个 C.5个 D.6个
2.(2017泰州)下列运算正确的是( )
A. B. C. D.
3.(2017孝感)下列计算正确的是( )
A. B.
C. D.
4.用大小相等的小正方形按一定规律拼成下列图形,则第个图形中小正方形的个数是( )
( http: / / www.21cnjy.com / )
A. B. C. D.
5.某种商品的进价为a元/件,在销 ( http: / / www.21cnjy.com )售旺季,商品售价较进价高30%;销售旺季过后,商品又以7折(即原售价的70%)的价格开展促销活动,这时一件该商品的售价为( )
A.a元 B.0.7a元 C.0.91a元 D.1.03a元
6.当时,代数式的值是( )
A. B. C. D.
7.已知,,求的值.我们可以用边长分别为x和y的两种正方形组成一个图形来解决这个问题,其中,能较为简单地解决这个问题的图形是( )
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
A B C D
8.若,则的值为( )
A. B. C. D.
9.(2017烟台)用棋子摆出下列一组图形:
( http: / / www.21cnjy.com / )
按照这种规律摆下去,第个图形用的棋子个数为 .
10.计算: .
11.三个连续整数中,是最大的一个,这三个数的和为 .
12.(2017泰州)已知,则代数式的值为 .
13.按一定规律排列的一列数:,,,,,,…,若,,表示这列数中的连续三个数,猜测,,满足的关系式是 .21世纪教育网版权所有
14.(2017安顺)若代数式是一个完全平方式,则 .
15.根据如图所示的程序计算,若输入x的值为1,则输出y的值为 .
( http: / / www.21cnjy.com / ) ( http: / / www.21cnjy.com / )
第15题图 第16题图
16.若一个大正方形和四个全等的小正方形按图 ( http: / / www.21cnjy.com )①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是 (用a,b的代数式表示).21教育网
17. 4个数排列成,我们称之为二项行列式.规定它的运算法则为:
.若,则 .
18.已知是方程的实根,求代数式的值.
19.先化简,再根据化简结果,你发现该代数式的值与的取值有什么关系?(不必说理)
20.选取二次三项式中的两项,配成完全平方式的过程叫配方.例如:
①选取二次项和一次项配方:;
②选取二次项和常数项配方:或
;
③选取一次项和常数项配方:.
根据上述材料,解决下面的问题:
(1)写出的两种不同形式的配方;
(2)已知,求的值.
参考答案
【课前热身】
1.1.08a 2. 3. 4.D 5.D 6.C
7.原式
8.原式,将代入,原式
【课堂互动】
知识点1 例1 0.8x 例2 A 跟踪训练 1. 2.
知识点2 例1 例2 D 跟踪训练 1. 2.
知识点3 例1 D 例2 跟踪训练 1.D 2. 3.
知识点4 例1 D 例2 原式
跟踪训练 1.C 2.
知识点5 例1 原式
当时,原式
例2 原式
因为,是一元二次方程的两个实数根
所以,则原式
跟踪训练 1.原式
当时,原式
2.原式
因为,所以原式
知识点6 例 验证:(1)因为,,
所以结果是5的3倍
(2)根据题意得:
因为,为整数,
所以它们的平方和是5的整数倍
延伸:余数为2
设任意三个连续整数中间的一个数为,则
因为……,所以余数为2
跟踪训练 1.(1)一
(2)
【课后作业】
1.B 2.C 3.B 4.C 5.C 6.B 7.B 8.B 9.
10. 11. 12. 13. 14.或 15. 16.17.21cnjy.com
18.原式,把代入方程得:,即:,则原式
19.原式,该代数式的值与的取值无关
20.(1);
(2)因为,
所以,所以,,
解得:,
所以
( http: / / www.21cnjy.com / )
…
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
