1.5 平方差公式的认识课件(第一课时)
文档属性
| 名称 | 1.5 平方差公式的认识课件(第一课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 795.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-10 00:00:00 | ||
图片预览







文档简介
课件22张PPT。1.5 平方差公式
第1课时 平方差公式的认识第一章 整式的乘除1.理解并掌握平方差公式的推导和应用.(重点)
2.理解平方差公式的结构特征,并能运用公式进行简单的运算.(难点)学习目标 从前,有-个狡猾的地主,把-块边长为20米的正方形土地租给张老汉种植.第二年,他对张老汉说:“我把这块地的-边减少5米,相邻的另-边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉-听,觉得好像没有吃亏,就答应道:“好吧.”回到家中,他把这事和
邻居们-讲,大家都说:“张
老汉,你吃亏了!”他非常吃惊.
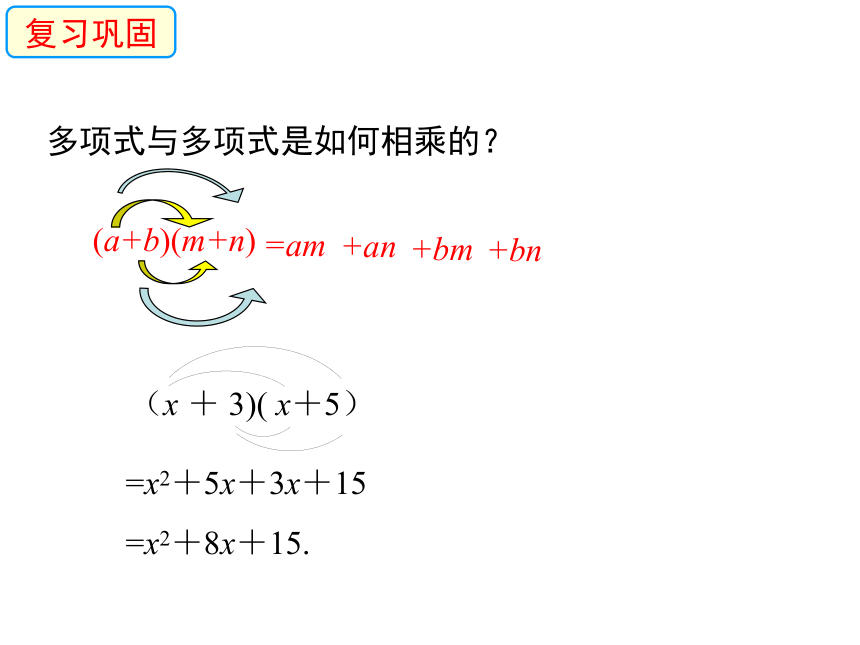
你知道张老汉是否吃亏了吗?情境导入多项式与多项式是如何相乘的? (x + 3)( x+5)=x2+5x+3x+15
=x2+8x+15. (a+b)(m+n)=am+an+bm+bn复习巩固①(x + 1)( x-1);
②(m + 2)( m-2);
③(2m+ 1)(2m-1);
④(5y + z)(5y-z).算一算:看谁算得又快又准.合作探究 ②(m+ 2)( m-2)=m2 -4③(2m+1)( 2m-1)=4m2-1④(5y+z)(5y-z)= 25y2 -z2 ①(x +1)( x- 1)=x2-1想一想:这些计算结果有什么特点?你发现了什么
规律? =x2 - 12=m2-22=(2m)2-12=(5y)2-z2两数和与这两数差的积,等于这两数的平方的差.合作探究(a+b)(a?b)=a2?b2两数和与这两数差的积,等于这两数的平方差.公式变形:(a–b) (a+b) =a2?b2 (b+a)(?b+a )=a2?b2平方差公式:你觉得这个公式有什么特征?在使用这个公式时应该注意什么?相乘的两个括号中有一对相同的数(式子),
有一对互为相反数的数(式子)找清哪个是相同的,即公式中的a;
哪个是互为相反数的,即公式中的b总结出平方差公式对我们有什么帮助?可以使我们在计算这种类型的多项式乘法时
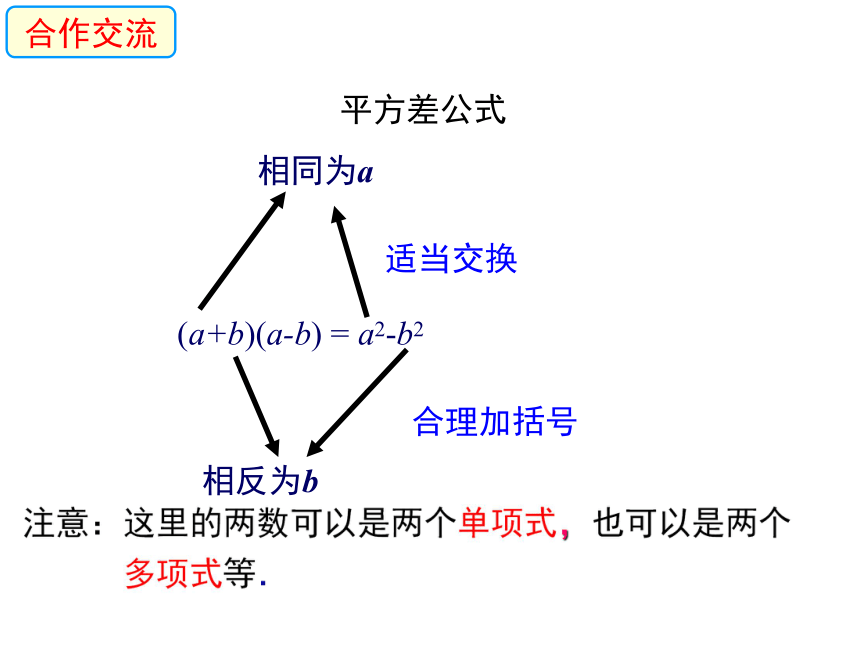
直接用公式更加快速和简便合作交流平方差公式注意:这里的两数可以是两个单项式,也可以是两个
多项式等. (a+b)(a-b) = a2-b2适当交换合理加括号合作交流口答下列各题:
(l)(-a+b)(a+b)=_________.
(2)(a-b)(b+a)= __________.
(3)(-a-b)(-a+b)= ________.
(4)(a-b)(-a-b)= _________.a2-b2a2-b2b2-a2b2-a2(1+x)(1-x)(-3+a)(-3-a)(0.3x-1)(1+0.3x)(1+a)(-1+a)aba2-b21x-3a12-x2(-3)2-a2a1a2-12 0.3x1( 0.3x)2-12(a-b)(a+b)2.下列式子可用平方差公式计算吗? 为什么? 如
果能够,怎样计算? (1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) (不能) (不能) ( 能 ) (不能) ?(a2 ?b2)= ?a2 + b2 ;例1 利用平方差公式计算:
(1) (5+6x )( 5-6x ) ; (2) (x-2y)(x+2y);
(3) (-m+n)(-m-n)解:(1)原式=52-(6x)2=25-36x2;
(2)原式=x2-(2y)2=x2 - 4y2;
(3)原式=(-m)2-n2=m2-n2.
典型精析例2 利用平方差公式计算:解:(1)原式=(1)原式=(ab)2-82
=a2b2-64.典型精析(3)(-7m+8n)(-8n-7m);
(4)(x-2)(x+2)(x2+4).解:(3)原式=(-7m)2-(8n)2
=49m2-64n2;
(4)原式=(x2-4)(x2+4)
=x4-16.利用平方差公式计算:典型精析例3 先化简,再求值:(2x-y)(y+2x)-(2y+
x)(2y-x),其中x=1,y=2.解:(2x-y)(y+2x)-(2y+x)(2y-x)
=4x2-y2- (4y2-x2)
=4x2-y2-4y2+x2=5x2-5y2.
当x=1,y=2时,原式=5×12-5×22=-15.典型精析 从前,有-个狡猾的地主,把-块边长为20米的正方形土地租给张老汉种植.第二年,他对张老汉说:“我把这块地的-边减少5米,相邻的另-边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉-听,觉得好像没有吃亏,就答应道:“好吧.”回到家中,他把这事和邻居们-讲,大家都说:“张老汉,你吃亏了!”他非常吃惊.
你知道张老汉是否吃亏了吗?解决问题请同学们运用今天所学知识帮张老汉算一下是否吃亏?1. 下面各式的计算对不对?如果不对,应怎样改正 ?(1)(x-2)(x+2)=x2-2;(2)(-2x-1)(2x-1)=4x2-1.不对,应是:x2-4.不对. 应是:1-4x2(6)(x-2)(-x+2)=x2-4;不对. 不能用平方差公式计算。(3) (1+2x)(1?2x)=1?2x2 (4) (2a2+b2)(2a2?b2)=2a4?b4(5) (3m+2n)(3m?2n)=3m2?2n2纠错练习不对. 应是:1-4x2不对,应是:4a4-b4.不对,应是:9m2-4n2.当堂检测(1)(a+3b)(a- 3b);解:原式=(2a+3)(2a-3)
=(2a)2-32
=4a2-9;=a2-9b2 ;解:原式=a2-(3b)2 (2)(3+2a)(-3+2a);2.利用平方差公式计算:(3)(-2x2-y)(-2x2+y);解:原式=(-2x2 )2-y2
=4x4-y2.
(4)(-5+6x)(-6x-5).解:原式=(-5+6x)(-5-6x)
=(-5)2-(6x)2
=25-36x2.平方差公式内容注意两个数的和与这两个数的差的积,等于这两个数的平方差1.符号表示:(a+b)(a-b)=a2-b22.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用课堂小结课后作业2、《作业本》P91、课本P21知识技能第1题
第1课时 平方差公式的认识第一章 整式的乘除1.理解并掌握平方差公式的推导和应用.(重点)
2.理解平方差公式的结构特征,并能运用公式进行简单的运算.(难点)学习目标 从前,有-个狡猾的地主,把-块边长为20米的正方形土地租给张老汉种植.第二年,他对张老汉说:“我把这块地的-边减少5米,相邻的另-边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉-听,觉得好像没有吃亏,就答应道:“好吧.”回到家中,他把这事和
邻居们-讲,大家都说:“张
老汉,你吃亏了!”他非常吃惊.
你知道张老汉是否吃亏了吗?情境导入多项式与多项式是如何相乘的? (x + 3)( x+5)=x2+5x+3x+15
=x2+8x+15. (a+b)(m+n)=am+an+bm+bn复习巩固①(x + 1)( x-1);
②(m + 2)( m-2);
③(2m+ 1)(2m-1);
④(5y + z)(5y-z).算一算:看谁算得又快又准.合作探究 ②(m+ 2)( m-2)=m2 -4③(2m+1)( 2m-1)=4m2-1④(5y+z)(5y-z)= 25y2 -z2 ①(x +1)( x- 1)=x2-1想一想:这些计算结果有什么特点?你发现了什么
规律? =x2 - 12=m2-22=(2m)2-12=(5y)2-z2两数和与这两数差的积,等于这两数的平方的差.合作探究(a+b)(a?b)=a2?b2两数和与这两数差的积,等于这两数的平方差.公式变形:(a–b) (a+b) =a2?b2 (b+a)(?b+a )=a2?b2平方差公式:你觉得这个公式有什么特征?在使用这个公式时应该注意什么?相乘的两个括号中有一对相同的数(式子),
有一对互为相反数的数(式子)找清哪个是相同的,即公式中的a;
哪个是互为相反数的,即公式中的b总结出平方差公式对我们有什么帮助?可以使我们在计算这种类型的多项式乘法时
直接用公式更加快速和简便合作交流平方差公式注意:这里的两数可以是两个单项式,也可以是两个
多项式等. (a+b)(a-b) = a2-b2适当交换合理加括号合作交流口答下列各题:
(l)(-a+b)(a+b)=_________.
(2)(a-b)(b+a)= __________.
(3)(-a-b)(-a+b)= ________.
(4)(a-b)(-a-b)= _________.a2-b2a2-b2b2-a2b2-a2(1+x)(1-x)(-3+a)(-3-a)(0.3x-1)(1+0.3x)(1+a)(-1+a)aba2-b21x-3a12-x2(-3)2-a2a1a2-12 0.3x1( 0.3x)2-12(a-b)(a+b)2.下列式子可用平方差公式计算吗? 为什么? 如
果能够,怎样计算? (1) (a+b)(?a?b) ;
(2) (a?b)(b?a) ;
(3) (a+2b)(2b+a);
(4) ?(a?b)(a+b) ;
(5) (?2x+y)(y?2x). (不能) (不能) (不能) ( 能 ) (不能) ?(a2 ?b2)= ?a2 + b2 ;例1 利用平方差公式计算:
(1) (5+6x )( 5-6x ) ; (2) (x-2y)(x+2y);
(3) (-m+n)(-m-n)解:(1)原式=52-(6x)2=25-36x2;
(2)原式=x2-(2y)2=x2 - 4y2;
(3)原式=(-m)2-n2=m2-n2.
典型精析例2 利用平方差公式计算:解:(1)原式=(1)原式=(ab)2-82
=a2b2-64.典型精析(3)(-7m+8n)(-8n-7m);
(4)(x-2)(x+2)(x2+4).解:(3)原式=(-7m)2-(8n)2
=49m2-64n2;
(4)原式=(x2-4)(x2+4)
=x4-16.利用平方差公式计算:典型精析例3 先化简,再求值:(2x-y)(y+2x)-(2y+
x)(2y-x),其中x=1,y=2.解:(2x-y)(y+2x)-(2y+x)(2y-x)
=4x2-y2- (4y2-x2)
=4x2-y2-4y2+x2=5x2-5y2.
当x=1,y=2时,原式=5×12-5×22=-15.典型精析 从前,有-个狡猾的地主,把-块边长为20米的正方形土地租给张老汉种植.第二年,他对张老汉说:“我把这块地的-边减少5米,相邻的另-边增加5米,继续租给你,租金不变,你也没有吃亏,你看如何?”张老汉-听,觉得好像没有吃亏,就答应道:“好吧.”回到家中,他把这事和邻居们-讲,大家都说:“张老汉,你吃亏了!”他非常吃惊.
你知道张老汉是否吃亏了吗?解决问题请同学们运用今天所学知识帮张老汉算一下是否吃亏?1. 下面各式的计算对不对?如果不对,应怎样改正 ?(1)(x-2)(x+2)=x2-2;(2)(-2x-1)(2x-1)=4x2-1.不对,应是:x2-4.不对. 应是:1-4x2(6)(x-2)(-x+2)=x2-4;不对. 不能用平方差公式计算。(3) (1+2x)(1?2x)=1?2x2 (4) (2a2+b2)(2a2?b2)=2a4?b4(5) (3m+2n)(3m?2n)=3m2?2n2纠错练习不对. 应是:1-4x2不对,应是:4a4-b4.不对,应是:9m2-4n2.当堂检测(1)(a+3b)(a- 3b);解:原式=(2a+3)(2a-3)
=(2a)2-32
=4a2-9;=a2-9b2 ;解:原式=a2-(3b)2 (2)(3+2a)(-3+2a);2.利用平方差公式计算:(3)(-2x2-y)(-2x2+y);解:原式=(-2x2 )2-y2
=4x4-y2.
(4)(-5+6x)(-6x-5).解:原式=(-5+6x)(-5-6x)
=(-5)2-(6x)2
=25-36x2.平方差公式内容注意两个数的和与这两个数的差的积,等于这两个数的平方差1.符号表示:(a+b)(a-b)=a2-b22.紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;不能直接应用公式的,要经过变形才可以应用课堂小结课后作业2、《作业本》P91、课本P21知识技能第1题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
