3.2 图形的旋转（1）同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
3.2 图形的旋转（1）同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
1.在平面内,将一个图形绕一个定点按某个 ( http: / / www.21cnjy.com )方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角,旋转图形不改变图形的形状和大小．
2.一个图形和它经过旋转所得的图形中,对应 ( http: / / www.21cnjy.com )点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等．
3.“将一个图形绕一定点沿某个方向转动一个 ( http: / / www.21cnjy.com )角度”意味着图形上的每个点都按相同的方式转动相同的角度．与平移类似,“旋转不改变图形的形状与大小”．
4.旋转图形的三要素:①旋转中心;②旋转方向;③旋转角．
基础知识和能力拓展训练
一、选选题
1．如图,由“基本图案”正方形ABCO绕O点顺时针旋转90°后的图形是(　　)
( http: / / www.21cnjy.com / )
A. ( http: / / www.21cnjy.com / ) B. ( http: / / www.21cnjy.com / ) C. ( http: / / www.21cnjy.com / ) D. ( http: / / www.21cnjy.com / )
2．下列图形中，绕某个点旋转90°能与自身重合的有( )
①正方形；②长方形；③等边三角形；④线段；⑤角；⑥平行四边形．
A. 1个 B. 2个 C. 3个 D. 4个
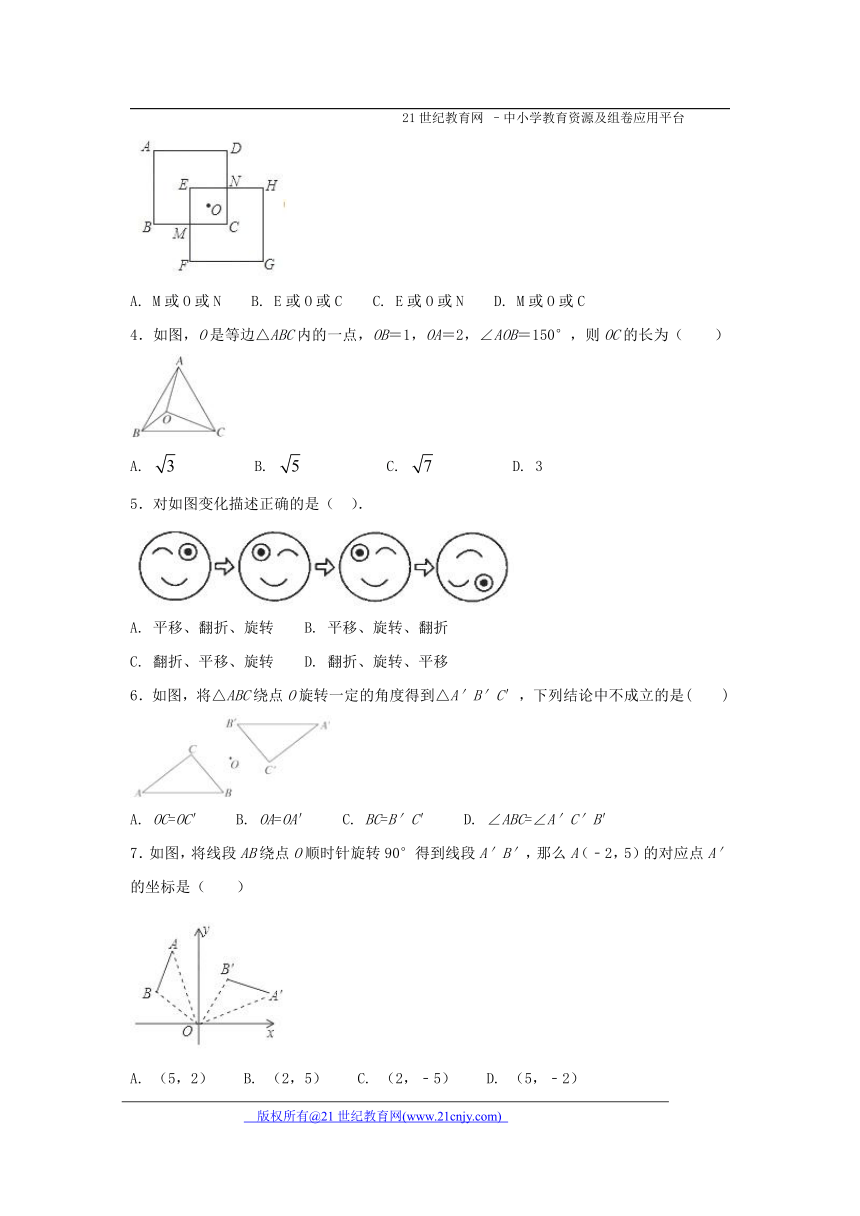
3．如图，若正方形EFGH由正方形ABCD绕某点旋转得到，则可以作为旋转中心的是（　　）
( http: / / www.21cnjy.com / )
A. M或O或N B. E或O或C C. E或O或N D. M或O或C
4．如图，O是等边△ABC内的一点，OB＝1，OA＝2，∠AOB＝150°，则OC的长为（ ）
( http: / / www.21cnjy.com / )
A. B. C. D. 3
5．对如图变化描述正确的是（ ）．
( http: / / www.21cnjy.com / )
A. 平移、翻折、旋转 B. 平移、旋转、翻折
C. 翻折、平移、旋转 D. 翻折、旋转、平移
6．如图，将△ABC绕点O旋转一定的角度得到△A′B′C′，下列结论中不成立的是( )
( http: / / www.21cnjy.com / )
A. OC=OC′ B. OA=OA′ C. BC=B′C′ D. ∠ABC=∠A′C′B′
7．如图，将线段AB绕点O顺时针旋转90°得到线段A′B′，那么A（﹣2，5）的对应点A′的坐标是（　　）
( http: / / www.21cnjy.com / )
A. （5，2） B. （2，5） C. （2，﹣5） D. （5，﹣2）
8．（2017湖北孝感第8 ( http: / / www.21cnjy.com )题） 如图，在平面直角坐标系中，点的坐标为 ，以原点为中心，将点顺时针旋转得到点，则点坐标为（ ）
( http: / / www.21cnjy.com / )
A. B. C. D.
9．下列说法正确的是（ ）
A. 平移不改变图形的形状和大小，而旋转则改变图形的形状和大小
B. 平移和旋转的共同点是改变图形的位置
C. 图形可以向某个方向平移一定距离，也可以向某方向旋转一定距离
D. 经过旋转，对应角相等，对应线段一定相等且平行
10．如图，将ΔABC绕点C顺时针旋转 ( http: / / www.21cnjy.com )，点B的对应点为点E，点A的对应点为点D，当点E恰好落在边AC上时，连接AD，若∠ACB=30°，则∠DAC的度数是（ ）
( http: / / www.21cnjy.com / )
A. 60° B. 65° C. 70° D. 75°
二、填空题
11．两个全等的三角尺重叠放在△A ( http: / / www.21cnjy.com )CB的位置，将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F．已知∠ACB=∠DCE=90°，∠B=30°，AB=8cm，则CF=_________cm．21世纪教育网版权所有
( http: / / www.21cnjy.com / )
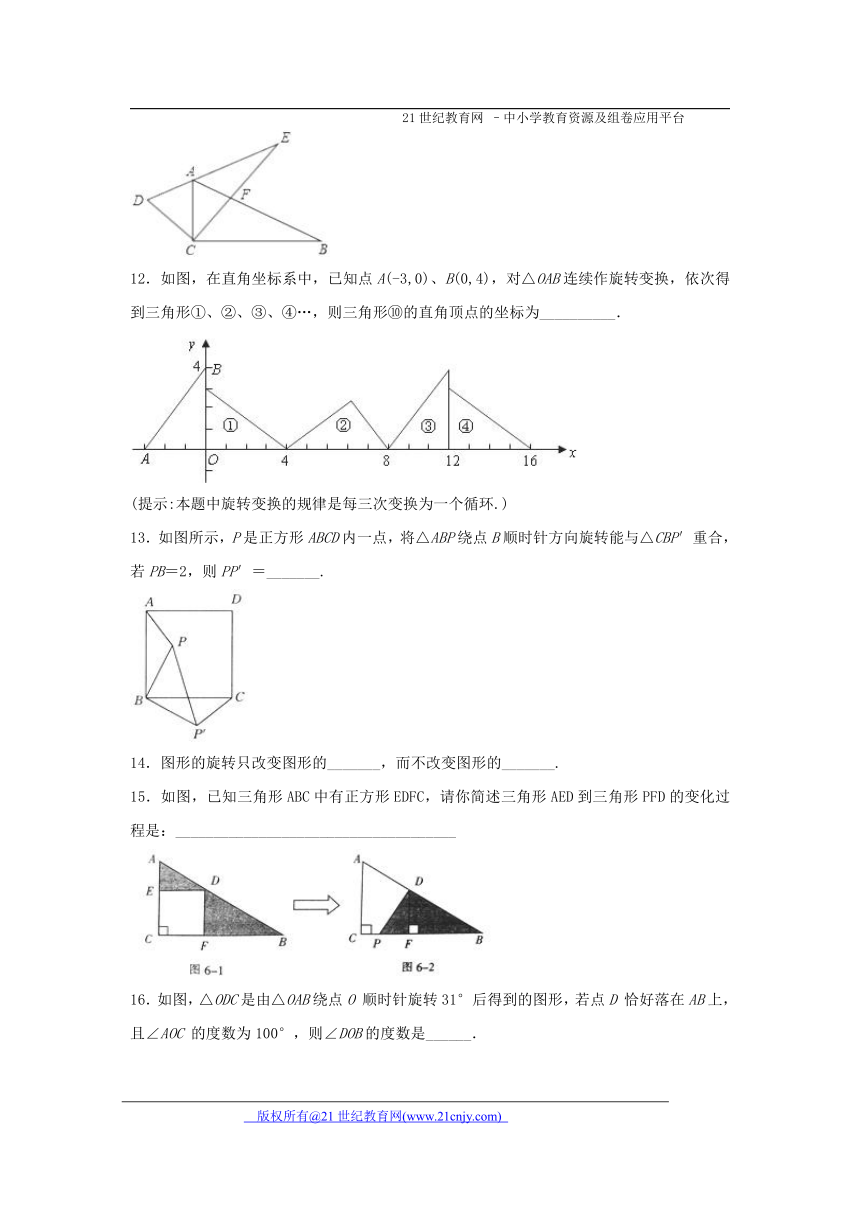
12．如图，在直角坐标系中，已知点 ( http: / / www.21cnjy.com )A(-3,0)、B(0,4)，对△OAB连续作旋转变换，依次得到三角形①、②、③、④…，则三角形⑩的直角顶点的坐标为__________．
( http: / / www.21cnjy.com / )
(提示:本题中旋转变换的规律是每三次变换为一个循环.)
13．如图所示，P是正方形ABCD内一点，将△ABP绕点B顺时针方向旋转能与△CBP′重合，若PB＝2，则PP′＝_______.2·1·c·n·j·y
( http: / / www.21cnjy.com / )
14．图形的旋转只改变图形的_______，而不改变图形的_______.
15．如图，已知三角形ABC中有正方形EDF ( http: / / www.21cnjy.com )C，请你简述三角形AED到三角形PFD的变化过程是：_____________________________________
( http: / / www.21cnjy.com / )
16．如图，△ODC是由△ ( http: / / www.21cnjy.com )OAB绕点O 顺时针旋转31°后得到的图形，若点D 恰好落在AB上，且∠AOC 的度数为100°，则∠DOB的度数是______．
( http: / / www.21cnjy.com / )
三、解答题
17．如图所示，边长为4的正方形ABCD绕点D逆时针旋转30°后能与四边形A′B′C′D′重合．
(1)旋转中心是哪一点
(2)四边形A′B′C′D′，是怎样的图形 面积是多少
(3)求∠C′DC和∠CDA′的度数；
(4)连接AA′，求∠DAA′的度数．
( http: / / www.21cnjy.com / )
18．如图，钟表的分针匀速旋转一周需要60分钟，那么：
（1）它的旋转中心是什么？
( http: / / www.21cnjy.com / )
（2）分针旋转一周，时针旋转多少度？
（3）上午8点整，时针和分针的夹角是多少？8点半呢？
19．平面直角坐标系中，有一Rt△ABC，且A（﹣1，3），B（﹣3，﹣1），C（﹣3，3），已知△A1AC1是由△ABC旋转得到的．2-1-c-n-j-y
（1）请写出旋转中心的坐标是　 　，旋转角是　 　度；
（2）以（1）中的旋转中心为中心，分别画出△A1AC1顺时针旋转90°、180°的三角形．
( http: / / www.21cnjy.com / )
20．如图，在Rt△ABC中，∠ACB=90°，△DCE是△ABC绕着点C顺时针方向旋转得到的，此时B、C、E在同一直线上．【版权所有：21教育】
（1）旋转角的大小；
（2）若AB=10，AC=8，求BE的长．
( http: / / www.21cnjy.com / )
21．如图,把长方形ABCD旋转到长方形GBEF的位置,此时点A,B,E在一条直线上.
(1)指出这个过程中的旋转中心,并说明旋转角度数是多少;
(2)指出图中的对应线段;
(3)连接BD,BF,DF,判断△DBF的形状,并说明理由.
( http: / / www.21cnjy.com / )
22．如图，AC是正方形ABCD的对角线，△ABC经过旋转后到达△AEF的位置．
(1)指出它的旋转中心；
(2)说出它的旋转方向和旋转角是多少度；
(3)分别写出点A，B，C的对应点．
( http: / / www.21cnjy.com / )
参考答案
1．A
【解析】试题解析：正方形ABCO绕O点顺时针旋转90°后的图形如图：
( http: / / www.21cnjy.com / )
故选A．
点睛：本题考查旋转的性质 ( http: / / www.21cnjy.com )：旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．要注意旋转的三要素：①定点-旋转中心；②旋转方向；③旋转角度．
2．A
【解析】①正方形旋转的最小的能与自身重合的度数是90度，正确；
②长方形旋转的最小的能与自身重合的度数是180度，错误；
③等边三角形旋转的最小的能与自身重合的度数是120度，错误；
④线段旋转的最小的能与自身重合的度数是180度，错误；
⑤角旋转的最小的能与自身重合的度数是360度，错误；
⑥平行四边形旋转的最小的能与自身重合的度数是180度，错误．
故选A．
3．A
【解析】试题分析：若以M为旋转中心，把 ( http: / / www.21cnjy.com )正方形ABCD顺时针旋转90°，A点对应点为H，B点对应点为E，C点对应点为F，D点对应点为G，则可得到正方形EFGH；
若以O为旋转中心，把正方形ABCD旋转180°，A点对应点为G，B点对应点为H，C点对应点为E，D点对应点为F，则可得到正方形EFGH；www.21-cn-jy.com
若以N为旋转中心，把正方形ABCD逆时 ( http: / / www.21cnjy.com )针旋转90°，A点对应点为F，B点对应点为G，C点对应点为H，D点对应点为E，则可得到正方形EFGH．21·世纪*教育网
故选A．
4．B
【解析】如图，将△AOB绕B点顺时针旋转60°到△BO′C的位置，
( http: / / www.21cnjy.com / )
由旋转的性质，得BO=BO′，
∴△BO′O为等边三角形，
由旋转的性质可知∠BO′C=∠AOB=150°，
∴∠CO′O=150°-60°=90°，
又∵OO′=OB=1，CO′=AO=2，
∴在Rt△COO′中，由勾股定理，得OC= ．
故选B．
5．C
【解析】解：第一个图变到第二个图是翻折，第二个图变到第三个图是平移，第三个图变到第四个图是旋转．故选C．【来源：21·世纪·教育·网】
6．D
【解析】根据旋转的性质，可知旋转前后的图形全等，而且对应角相等，对应边相等，D选项中不是对应角.
故选：D.
7．A
【解析】试题解析：作AD⊥x轴于点D，作A′D′⊥x轴于点D′，
( http: / / www.21cnjy.com / )
则OD=A′D′，AD=OD′，OA=OA′，
∴△OAD≌△A′OD′（SSS），
∵A（-2，5），
∴OD=2，AD=5，
∴点A′的坐标为（5，2），
故选A．
8．D
【解析】试题分析：作AB⊥x轴于点B，
( http: / / www.21cnjy.com / )
∴AB=，OB=1，则tan∠AOB==，
∴∠AOB=60°，
∴∠AOy=30°
∴将点A顺时针旋转150°得到点A′后，如图所示，
OA′=OA= =2，∠A′OC=30°，
∴A′C=1，OC=，即A′（，﹣1），
故选D．
9．B
【解析】试题分析：A、平移和旋转都不改变图形的形状和大小，故此选项错误；
B、平移和旋转改变的只是图形的位置，故此选项正确；
C、图形可以向某个方向平移一定的距离，也可以绕某点旋转一定的角度，故此选项错误；
D、经过旋转，对应角相等，对应线段一定相等但不一定平行，故此选项错误．
故选B．
10．D
【解析】解：由题意知：△ABC≌△ ( http: / / www.21cnjy.com )DEC，∴∠ACB=∠DCE=30°，AC=DC，∴∠DAC=（180° ∠DCA）÷2=（180° 30°）÷2=75°．故选D．21*cnjy*com
点睛：本题主要考查了旋转的性质，解题的关 ( http: / / www.21cnjy.com )键是掌握旋转的性质：①对应点到旋转中心的距离相等．②对应点与旋转中心所连线段的夹角等于旋转角．③旋转前、后的图形全等．
11．
【解析】试题解析∵将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，【出处：21教育名师】
∴DC=AC，∠D=∠CAB，
∴∠D=∠DAC，
∵∠ACB=∠DCE=90°，∠B=30°，
∴∠D=∠CAB=60°，
∴∠DCA=60°，
∴∠ACF=30°，
可得∠AFC=90°，
∵AB=8cm，
∴AC=4cm，
∴FC=4cos30°=2cm．
【点睛】此题主要考查了旋转的性质以及直角三角形的性质，正确得出∠AFC的度数是解题关键．
12．（36，0）.
【解析】试题解析：由原图到图③，相当 ( http: / / www.21cnjy.com )于向右平移了12个单位长度，象这样平移三次直角顶点是（36，0），再旋转一次到三角形⑩，直角顶点仍然是（36，0），则三角形⑩的直角顶点的坐标为（36，0）．21·cn·jy·com
13．
【解析】解：∵四边形ABCD为正方形，∴∠ABC=90°．∵△ABP绕点B顺时针方向旋转能与△CBP′重合，∴∠PBP′=∠ABC=90°，PB=P′B=2，∴△PBP′为等腰直角三角形，∴PP′=PB=．21教育名师原创作品
故答案为： ．
点睛：本题考查了旋转的性质：旋转前后两 ( http: / / www.21cnjy.com )图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了正方形与等腰直角三角形性质．
14． 位置 形状和大小
【解析】根据图形的旋转的性质，可知图形的旋转只改变图形的位置，而不改变图形的形状和大小.
故答案为：位置，形状和大小.
15．以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD
【解析】试题分析：由图可知三角 ( http: / / www.21cnjy.com )形AED到三角形PFD，点D位置不变，点A至点P，点E至点F，AD＝PD，ED＝FD，根据旋转的性质可知：以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD．21*cnjy*com
故答案为：以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD．
16．38°　
【解析】由题意得
∠AOD=∠BOC=31°,
∵∠AOC =100°，
∴∠DOB=∠AOC-∠AOD=∠BOC
=100°-31°-31°
=38°.
17．（1）点D（2）边长为4的正方形，16（3）30°，60°（4）75°
【解析】试题分析：（1）根据题意可得旋转中心是D点；
（2）因为四边形A′B′C′D′是由正方形ABCD旋转得到的，所以它是和四边形ABCD全等的正方形，边长还是4；21教育网
（3）根据旋转的宗旨即可得到；
（4）根据等腰三角形的性质即可求解.
试题解析：(1)旋转中心是点D.
(2)四边形A′B′C′D′是正方形， ( http: / / www.21cnjy.com )旋转不改变图形的大小，四边形A′B′C′D′是正方形ABCD旋转得来的，而正方形ABCD的面积为16，所以四边形A′B′C′D′的面积是16．
(3)因为C与C′是对应点，而对应点与旋转 ( http: / / www.21cnjy.com )中心连线所成的角即是旋转角，由题意知图形绕点D旋转30°，所以∠C′DC＝30°．又因为四边形A′B′C′D′是正方形，所以∠C′DA′＝90°，而∠C′DC＝30°，所以∠CDA′＝60°． 21cnjy.com
(4)根据旋转的特征，对应点 ( http: / / www.21cnjy.com )到旋转中心的距离相等，所以由点D，A，A′所确定的三角形是等腰三角形，AD＝A′D，而∠ADA′＝30°，所以∠DAA′＝∠DA′A＝（180°-30°）÷2=75°.
点睛：此题主要考查了旋转的性质：对应点 ( http: / / www.21cnjy.com )与旋转中心所连线段的夹角等于旋转角；对应点到旋转中心的距离相等；旋转前、后的图形全等，也考查了正方形的性质和等腰三角形的性质.
18．（1）表盘中心（2）30°（3）120°，75°
【解析】试题分析：（1）观察得到旋转中心是表盘中心；
（2）分针旋转一周，时针旋转一小时，即360°的十二分之一；
（3）分针每分钟转6°，时针每分钟转0.5°， 利用钟表表盘的特征根据分针、时针转动的度数即可求解.
试题解析：（1）它的旋转中心是表盘中心；
（2）分针旋转一周，时针旋转30度，因为一圈为360度，而一圈为12小时，所以一小时就是360度除以12，即一小时为30度；
（3）8点整，时针指向8，分针指向12，钟表12个数字，每相邻两个数字之间的夹角为30°，
因此8点整分针与时针的夹角正好是4×30°=120°；
8点半：时针与分针的夹角为：30°×8+0.5°×30-6°×30=75°.
19．（1）旋转中心的坐标是（0，0），旋转角是90度；（2）画图见解析.
【解析】（1）根据网格结构，找出对应点连线的垂直平分线的交点即为旋转中心，一对对应点与旋转中心连线的夹角即为旋转角；【来源：21cnj*y.co*m】
（2）根据网格结构分别找出找出△A1AC1顺时针旋转90°、180°后的对应点的位置，然后顺次连接即可．
解：（1）旋转中心的坐标是（0，0），旋转角是90度；
（2）如图所示，△A1A2C2是△A1AC1以O为旋转中心，顺时针旋转90°的三角形，
△A2C3B是△A1AC1以O为旋转中心，顺时针旋转180°的三角形．
( http: / / www.21cnjy.com / )
20．（1）90°；（2）14．
【解析】试题分析：（1）根据题意∠AC ( http: / / www.21cnjy.com )E即为旋转角，只需求出∠ACE的度数即可．
（2）根据勾股定理可求出BC，由旋转的性质可知CE=CA=8，从而可求出BE的长度．
试题解析：（1）∵△DCE是△ABC绕着点C顺时针方向旋转得到的，此时点B、C、E在同一直线上，
∴∠ACE=90°，即旋转角为90°，
（2）在Rt△ABC中，
∵AB=10，AC=8，
∴BC==6，
∵△ABC绕着点C旋转得到△DCE，
∴CE=CA=8，
∴BE=BC+CE=6+8=14www-2-1-cnjy-com
21．(1)旋转中心为点B,旋转角度数是 ( http: / / www.21cnjy.com )90°；(2)对应线段:AB与GB,AD与GF,DC与FE,BC与BE；(3)△DBF是等腰直角三角形，理由见解析.
【解析】试题分析：（1）由长方形的性质得出∠ ( http: / / www.21cnjy.com )ABC=90°，由已知条件和旋转的性质得出∠CBE=180°-90°=90°，得出旋转中心是点B，旋转角度数是90°；
（2）由旋转的性质得出长方形GBEF≌长方形ABCD，得出BG=BA，BE=BC，EF=CD，GF=AD，即可得出结果；
（3）由旋转的性质得：BF=BD，∠DBF=∠CBE=90°，即可得出结论．
试题解析：（1）∵四边形ABCD是长方形，
∴∠ABC=90°，
∵把长方形ABCD旋转到长方形GBEF的位置，此时点A，B，E在一条直线上，
∴∠CBE=180°-90°=90°，
∴旋转中心是点B，旋转角度数是90°；
（2）由旋转的性质得：长方形GBEF≌长方形ABCD，
∴BG=BA，BE=BC，EF=CD，GF=AD，BF=BD，
∴图中的对应线段为BG和BA，BE和BC，EF和CD，GF和AD，BF和BD；
（3）△DBF是等腰直角三角形；理由如下：
由旋转的性质得：BF=BD，∠DBF=∠CBE=90°，
∴△DBF是等腰直角三角形．
22．(1)A;(2) 旋转方向为逆时针方向，旋转角是45度；(3) A，E，F.
【解析】试题分析：(1)因为△ABC ( http: / / www.21cnjy.com )经过旋转后到达△AEF的位置,则A点的对应点为A,于是可判断旋转中心为点A; (2)根据旋转的性质求解; (3)根据旋转的性质求解.
解：（1）它的旋转中心为点A；
（2）它的旋转方向为逆时针方向，旋转角是45度；
（3）点A，B，C的对应点分别为点A，E，F.
( http: / / www.21cnjy.com / )
版权所有@21世纪教育网(www.21cnjy.com)