5.2.2平行的判定方法3(课件)
图片预览




文档简介
(共15张PPT)
5.2.2 平行线的判定方法三
人教版 七年级下
我们已经学习了,判断两条直线平行的方法
今天我们学习,判断两条直线平行的方法三
同位角相等,两直线平行。
内错角相等,两直线平行。
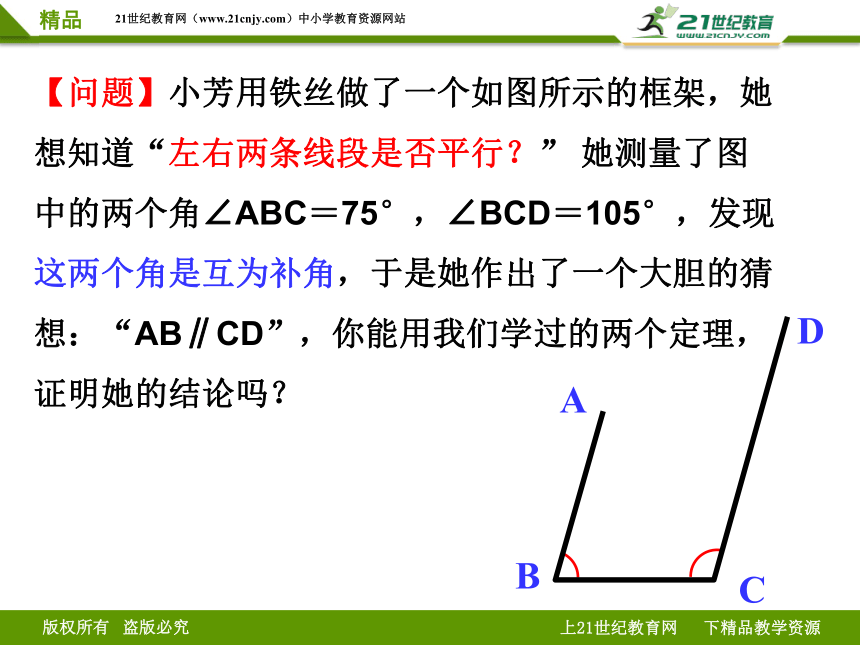
【问题】小芳用铁丝做了一个如图所示的框架,她想知道“左右两条线段是否平行?” 她测量了图中的两个角∠ABC=75°,∠BCD=105°,发现这两个角是互为补角,于是她作出了一个大胆的猜想:“AB∥CD”,你能用我们学过的两个定理,证明她的结论吗?
A
B
C
D
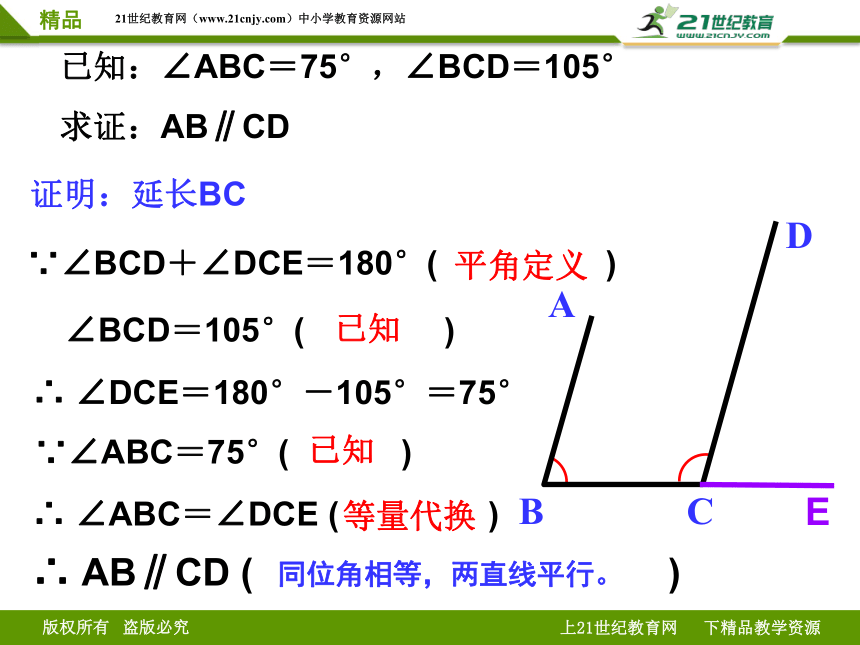
已知:∠ABC=75°,∠BCD=105°
求证:AB∥CD
A
B
C
D
证明:延长BC
E
∵∠BCD+∠DCE=180°( )
平角定义
∠BCD=105°( )
已知
∴ ∠DCE=180°-105°=75°
∵∠ABC=75°( )
已知
∴ ∠ABC=∠DCE ( )
等量代换
∴ AB∥CD ( )
同位角相等,两直线平行。
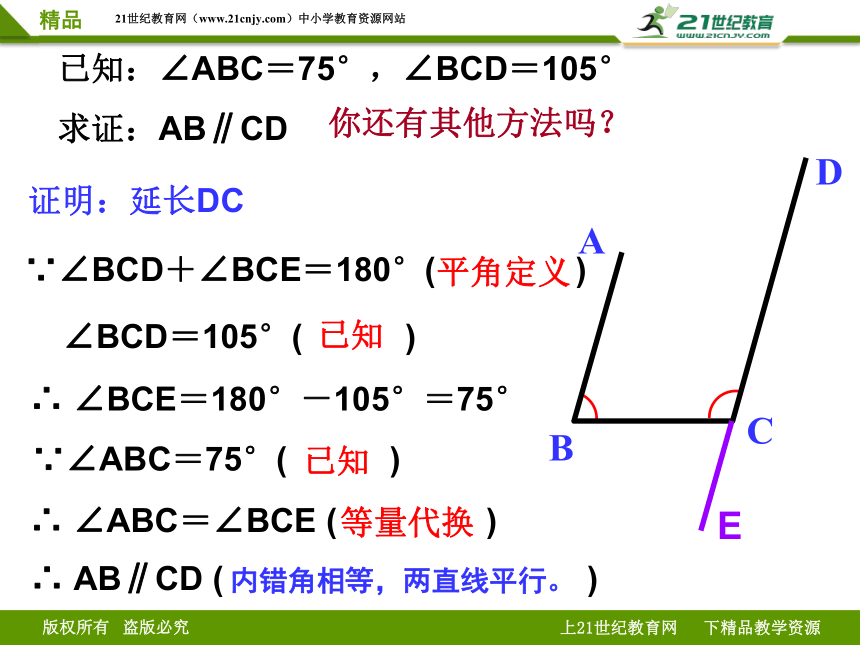
已知:∠ABC=75°,∠BCD=105°
求证:AB∥CD
A
B
C
D
证明:延长DC
E
∵∠BCD+∠BCE=180°( )
平角定义
∠BCD=105°( )
已知
∴ ∠BCE=180°-105°=75°
∵∠ABC=75°( )
已知
∴ ∠ABC=∠BCE ( )
等量代换
∴ AB∥CD ( )
内错角相等,两直线平行。
你还有其他方法吗?
由此,我们可以得到平行线的第三种判定方法:
同旁内角互补,两直线平行。
同位角相等,两直线平行。
内错角相等,两直线平行。
这样,我们就有三种判定直线平行方法
希望同学们,合理灵活地运用上述方法,去解决问题
【例】在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行吗?为什么?
c
a
b
1
2
解:这两条直线平行,理由如下:
∵ a⊥c (已知)
∴∠1=90° (垂直定义)
∵ b⊥c (已知)
∴∠2=90° (垂直定义)
∴∠1=∠2 (等量代换)
已知: a⊥c,b⊥c,求证: a∥b
∴a∥b (同位角相等,两直线平行)
c
a
b
1
2
由此得出:
已知: a⊥c ,b⊥c,求证: a∥b
垂直于同一条直线的两条直线互相平行。
a
b
c
已知: a∥c , b∥c,求证:a∥b
平行于同一条直线的两条直线互相平行。
平行公理的推论
平行线的判定综合练习
1、如图,∠1+∠2=180°,求证:AB∥CD
证明:∵∠1+∠2=180°( )
∠1=∠3 ( )
∠2=∠4 ( )
∴∠3+ =180°( )
∴ AB∥CD ( )
1
2
A
B
C
D
E
F
4
3
已知
对顶角相等
对顶角相等
∠4
等量代换
同旁内角互补,两直线平行。
∴∠1+∠2=180°( )
∴ EF∥GH ( )
证明:∵ ∠1+∠3=180°( )
等量代换
同旁内角互补,两直线平行
2、已知:∠2=∠3,∠1+∠3=180°, 求证:EF∥GH.
∠2=∠3 ( )
1
2
A
B
C
D
E
F
3
G
H
已知
已知
∴AD∥ ( )
∴AD∥ ( )
证明:∵∠DAF=∠AFE ( )
A
D
B
C
F
E
内错角相等,两直线平行
3、如图,已知:∠DAF=∠AFE,
∠D+∠C=180°,求证:EF∥BC
已知
EF
∵∠D+∠C=180°( )
已知
BC
同旁内角互补,两直线平行
∴EF∥BC ( )
平行于同一直线的两条直线互相平行
4、如图,∠1=∠2,BD平分∠ABC,
试说明:AD∥BC
A
B
C
D
1
2
3
证明:∵BD平分∠ABC(已知),
∴∠2=∠3 ( )
又∵∠1=∠2 ( )
∴∠1=∠3 ( )
∴AD∥BC ( )
角平分线定义
已知
等量代换
内错角相等,两直线平行
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
5.2.2 平行线的判定方法三
人教版 七年级下
我们已经学习了,判断两条直线平行的方法
今天我们学习,判断两条直线平行的方法三
同位角相等,两直线平行。
内错角相等,两直线平行。
【问题】小芳用铁丝做了一个如图所示的框架,她想知道“左右两条线段是否平行?” 她测量了图中的两个角∠ABC=75°,∠BCD=105°,发现这两个角是互为补角,于是她作出了一个大胆的猜想:“AB∥CD”,你能用我们学过的两个定理,证明她的结论吗?
A
B
C
D
已知:∠ABC=75°,∠BCD=105°
求证:AB∥CD
A
B
C
D
证明:延长BC
E
∵∠BCD+∠DCE=180°( )
平角定义
∠BCD=105°( )
已知
∴ ∠DCE=180°-105°=75°
∵∠ABC=75°( )
已知
∴ ∠ABC=∠DCE ( )
等量代换
∴ AB∥CD ( )
同位角相等,两直线平行。
已知:∠ABC=75°,∠BCD=105°
求证:AB∥CD
A
B
C
D
证明:延长DC
E
∵∠BCD+∠BCE=180°( )
平角定义
∠BCD=105°( )
已知
∴ ∠BCE=180°-105°=75°
∵∠ABC=75°( )
已知
∴ ∠ABC=∠BCE ( )
等量代换
∴ AB∥CD ( )
内错角相等,两直线平行。
你还有其他方法吗?
由此,我们可以得到平行线的第三种判定方法:
同旁内角互补,两直线平行。
同位角相等,两直线平行。
内错角相等,两直线平行。
这样,我们就有三种判定直线平行方法
希望同学们,合理灵活地运用上述方法,去解决问题
【例】在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行吗?为什么?
c
a
b
1
2
解:这两条直线平行,理由如下:
∵ a⊥c (已知)
∴∠1=90° (垂直定义)
∵ b⊥c (已知)
∴∠2=90° (垂直定义)
∴∠1=∠2 (等量代换)
已知: a⊥c,b⊥c,求证: a∥b
∴a∥b (同位角相等,两直线平行)
c
a
b
1
2
由此得出:
已知: a⊥c ,b⊥c,求证: a∥b
垂直于同一条直线的两条直线互相平行。
a
b
c
已知: a∥c , b∥c,求证:a∥b
平行于同一条直线的两条直线互相平行。
平行公理的推论
平行线的判定综合练习
1、如图,∠1+∠2=180°,求证:AB∥CD
证明:∵∠1+∠2=180°( )
∠1=∠3 ( )
∠2=∠4 ( )
∴∠3+ =180°( )
∴ AB∥CD ( )
1
2
A
B
C
D
E
F
4
3
已知
对顶角相等
对顶角相等
∠4
等量代换
同旁内角互补,两直线平行。
∴∠1+∠2=180°( )
∴ EF∥GH ( )
证明:∵ ∠1+∠3=180°( )
等量代换
同旁内角互补,两直线平行
2、已知:∠2=∠3,∠1+∠3=180°, 求证:EF∥GH.
∠2=∠3 ( )
1
2
A
B
C
D
E
F
3
G
H
已知
已知
∴AD∥ ( )
∴AD∥ ( )
证明:∵∠DAF=∠AFE ( )
A
D
B
C
F
E
内错角相等,两直线平行
3、如图,已知:∠DAF=∠AFE,
∠D+∠C=180°,求证:EF∥BC
已知
EF
∵∠D+∠C=180°( )
已知
BC
同旁内角互补,两直线平行
∴EF∥BC ( )
平行于同一直线的两条直线互相平行
4、如图,∠1=∠2,BD平分∠ABC,
试说明:AD∥BC
A
B
C
D
1
2
3
证明:∵BD平分∠ABC(已知),
∴∠2=∠3 ( )
又∵∠1=∠2 ( )
∴∠1=∠3 ( )
∴AD∥BC ( )
角平分线定义
已知
等量代换
内错角相等,两直线平行
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
