26.3实际问题与二次函数2（课件）

(共33张PPT)
26.3 实际问题与二次函数
人教版 七年级下
抛物线 y＝a(x－h)2＋k有如下特点：
⑴、① 当 a＞0 时，开口向上；
② 当 a＜0 时，开口向下。
⑵、对称轴是直线： x＝h
⑶、顶点坐标是： ( h，k )
一般地、函数 y＝ax2＋bx＋c (a≠0)
对称轴： x＝
顶点坐标：
利润＝售价－成本
总利润＝每件利润×件数
【探究1】某商品现在的售价为每件60元，每星期可卖出300件，商人甲采用提高售价，减少销售量的办法增加利润，市场调查反映：每涨价1元，每星期要少卖出10件。已知商品进价为每件40元。
⑴ 若提价15元，能获得多少利润？
解：⑴ (60＋15－40)×(300－15×10)
＝35×150
＝5250 (元)
⑵若要获得利润6000元，应如何定价？
【探究1】某商品现在的售价为每件60元，每星期可卖出300件，商人甲采用提高售价，减少销售量的办法增加利润，市场调查反映：每涨价1元，每星期要少卖出10件。已知商品进价为每件40元。
⑵ 设要获得6000元的利润，定价应为x元
(x－40)×[300－10×(x－60)]＝6000
整理，得 x2－130x＋4200＝0
解，得 x1＝60 (舍去)， x2＝70
答：要获得利润6000元，定价应为70元。
【探究1】某商品现在的售价为每件60元，每星期可卖出300件，商人甲采用提高售价，减少销售量的办法增加利润，市场调查反映：每涨价1元，每星期要少卖出10件。已知商品进价为每件40元。
⑶若要获得利润最大，应如何定价？
⑶ 设定价为x元，获得总利润为y元。
y＝(x－40)×[300－10×(x－60)]
＝－10x2＋1300x－36000
＝－10(x－65)2＋6250
答：定价应为65元时，获得最大利润是6250元。
(40≤x≤90)
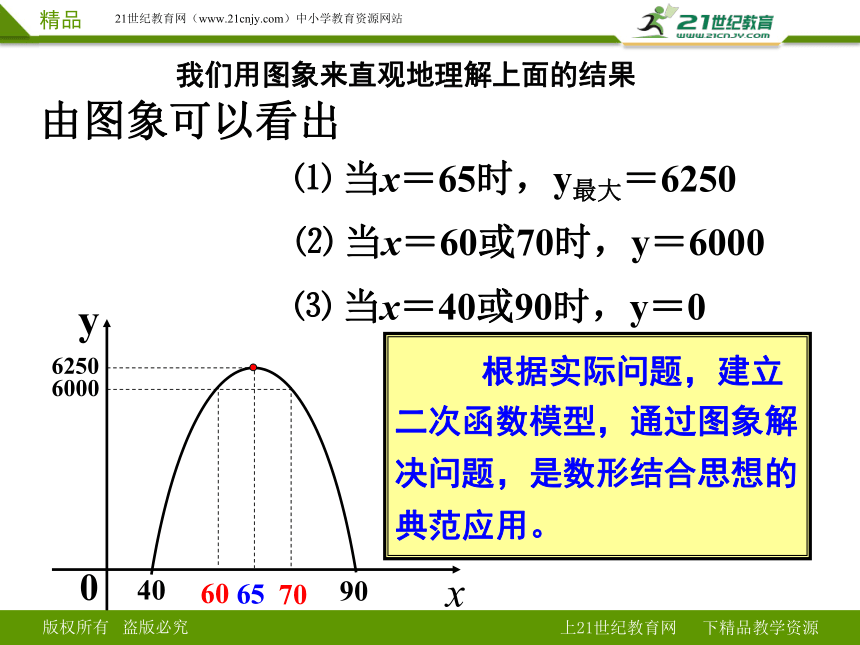
我们用图象来直观地理解上面的结果
y
由图象可以看出
⑴ 当x＝65时，y最大＝6250
6250
40
90
6000
x
0
65
70
60
⑵ 当x＝60或70时，y＝6000
⑶ 当x＝40或90时，y＝0
根据实际问题，建立二次函数模型，通过图象解决问题，是数形结合思想的典范应用。
【探究2】某商品现在的售价为每件60元，每星期可卖出300件，商人乙采用降低售价，增加销售量的办法增加利润，市场调查反映：每降价1元，每星期要多卖出20件。已知商品进价为每件40元，问：如何定价能使利润最大？
【探究2】某商品现在的售价为每件60元，每星期可卖出300件，商人乙采用降低售价，增加销售量的办法增加利润，市场调查反映：每降价1元，每星期要多卖出20件。已知商品进价为每件40元，问：如何定价能使利润最大？
解：设定价x元，获得总利润为y元。
y＝(x－40)×[300＋20(60－x)]
＝－20x2＋2300x－60000
＝－20(x－57.5)2＋6125
答：定价应为57.5元时，获得最大利润是6125元。
【探究2】某商品现在的售价为每件60元，每星期可卖出300件，商人乙采用降低售价，增加销售量的办法增加利润，市场调查反映：每降价1元，每星期要多卖出20件。已知商品进价为每件40元，问：如何定价能使利润最大？
解：设降价x元，获得总利润为y元。
y＝(60－x－40)×(300＋20x)
＝－20x2＋100x＋6125
＝－20(x－2.5)2＋6125
答：定价应为57.5元时，获得最大利润是5875元。
【探究】某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：每涨价2元，每星期少卖出20件；每降价2元，每星期可多卖出40件，已知商品的进价为每件40元，如何定价才能使利润最大？
将问题化为涨价和降价两种情况，
即利用分类讨论的思想去解决问题
【探究】某商品现在的售价为每件60元，每星期可卖出300件，市场调查反映：每涨价2元，每星期少卖出20件；每降价2元，每星期可多卖出40件，已知商品的进价为每件40元，如何定价才能使利润最大？
解：⑴ 设涨价x元，获得总利润为y元。
y＝(60＋x－40)×
解：⑴ 设涨价x元，获得总利润为y元。
y＝(60＋x－40)×
＝－10x2＋100x＋6000
＝5
＝6250
⑵ 设降价x元，获得总利润为y元。
y＝(60－x－40)×
＝－20x2＋100x＋6000
＝2.5
＝6125
答：综合涨价与降价两种情况及现在的销售状况可知，定价65元，利润最大。
归纳小结
运用二次函数的性质求实际问题的最大值
审清题意，明确各量关系,建立二次函数模型
利用抛物线的顶点求它的最大值
建立适当的坐标系可以直观地求解二次函数的问题
求出函数解析式和自变量的取值范围
课堂练习
1、旅馆有50个房间，每个房间定价为180元/天，房间会全部住满，若每个房间每天定价每增加10元时，就会有一个房间空闲，问：房价定为多少元？旅馆的营业额最大？
营业额＝房间定价×住房间数
1、旅馆有50个房间，每个房间定价为180元/天，房间会全部住满，若每个房间每天定价每增加10元时，就会有一个房间空闲，问：房价定为多少元？旅馆的营业额最大？
解：设房价定为x元，营业额为y元。
y＝x×
＝340
＝11560
答：房价定为340元，营业额最大为11560元。
变例：旅馆有50个房间，每个房间定价为180元/天，房间会全部住满，若每个房间每天定价每增加10元时，就会有一个房间空闲，如果旅馆需对每个房间每天支出20元各种费用，则房价定为多少元？旅馆的营业额最大？
营业额＝每间房价×住房间数－支出费用
变例：旅馆有50个房间，每个房间定价为180元/天，房间会全部住满，若每个房间每天定价每增加10元时，就会有一个房间空闲，如果旅馆需对每个房间每天支出20元各种费用，则房价定为多少元？旅馆的营业额最大？
营业额＝每间房价×住房间数－支出费用
解：设房价定为x元，营业额为y元。
y＝x×
－20x
营业额＝每间房价×住房间数－支出费用
解：设房价定为x元，营业额为y元。
y＝x×
－20x
＝240
＝5760
答：房价定为240元，营业额最大为5760元。
x(元) 15 20 30 …
y(件) 25 20 10 …
2、某产品每件成本10元，试销阶段每件产品的销售价 x(元)与产品的日销售量 y(件)之间的关系如下表：
若日销售量 y 是销售价 x 的一次函数。
⑴求出日销售量 y(件)与销售价 x (元)的函数关系式；
解： ⑴ 设此一次函数解析式为y＝kx＋b
则
解得：k=－1，b＝40
所求一次函数解析式为y＝－x＋40
⑵要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日销售利润是多少元？
⑵ 设每件产品的销售价应定为 x 元，
所获销售利润为 w 元。则
W＝(x－10) (－x＋40)
＝－x2＋50x－400
＝－(x－25)2＋225
答：销售价应定为25元，每日最大利润为225元。
3、某果园有100棵橙子树，每一棵树平均结600个橙子。现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子。若每个橙子市场售价约2元，问增种多少棵橙子树，果园的总产值最高，果园的总产值最高约为多少？
3、某果园有100棵橙子树，每一棵树平均结600个橙子。现准备多种一些橙子树以提高产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少。根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子。若每个橙子市场售价约2元，问增种多少棵橙子树，果园的总产值最高，果园的总产值最高约为多少？
解：设增种x棵橙子树，总产值为y元。
y＝(100＋x)×(600－5x)×2
＝－10x2＋200x＋120000
＝10
＝121000
答：增种10棵橙子树，总产值最高约为121000元。
4、某超市经销一种销售成本为每件40元的商品。据市场调查分析，如果按每件50元销售，一周能售出500件；若销售单价每涨1元，每周销量就减少10件。设销售单价为x元(x≥50)，一周的销售量为y件。
⑴写出y与x的函数关系式(标明x的取值范围)
解：⑴由题意，得
y＝500－10× (x－50)
y＝1000－10x
(50 ≤ x ≤ 100)
4、某超市经销一种销售成本为每件40元的商品。据市场调查分析，如果按每件50元销售，一周能售出500件；若销售单价每涨1元，每周销量就减少10件。设销售单价为x元(x≥50)，一周的销售量为y件。
⑵设一周的销售利润为S，写出S与x的函数关系式，并确定当单价在什么范围内变化时，利润随着单价的增大而增大？
⑵ S＝(x－40)×(1000－10x)
S＝－10x2＋1400x－40000
(50 ≤ x ≤ 100)
⑵设一周的销售利润为S，写出S与x的函数关系式，并确定当单价在什么范围内变化时，利润随着单价的增大而增大？
⑵ S＝(x－40)×(1000－10x)
S＝－10x2＋1400x－40000
＝－10(x－70)2＋9000
(50 ≤ x ≤ 100)
x
S
0 50 70 100
4000
9000
由图可知
当50 ≤ x ≤70时，
利润随着单价的增大而增大。
⑶在超市对该种商品投入不超过10000元的情况下，使得一周销售利润达到8000元，销售单价应定为多少？
⑶进货量＝10000÷40
＝250 (件)
y＝1000－10x＜250
x＞75
－10(x－70)2＋9000＝8000
解，得x1＝80，x2＝60
答：销售单价应定为80元。
谢谢
21世纪教育网（www.21cnjy.com)中小学教育资源网站
有大把优质资料？一线名师？一线教研员？
赶快加入21世纪教育网名师合作团队吧！！月薪过万不是梦！！
详情请看：http://www.21cnjy.com/zhaoshang/