17.1勾股定理(课件)
图片预览





文档简介
(共27张PPT)
勾股定理
人教版 八年级下
在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股。斜边叫做弦。
据我国古算书《周髀算经》记载,约公元前1100年,人们已经知道,如果勾是三、股是四,那么弦是五。后来人们进一步发现并证明了直角三角形三边之间的关系:两条直角边的平方和等于斜边的平方。你能发现这个关系吗?
上面的图案有什么意义?为什么选它作为2002年在北京召开的国际数学家大会的会徽?
学过本章,你就能回答上述问题了。本章中,我们将探索直角三角形的三边之间特有的数量关系,并运用所得结论解决问题。
ICM 2002
Beijing
August 20-28. 2002
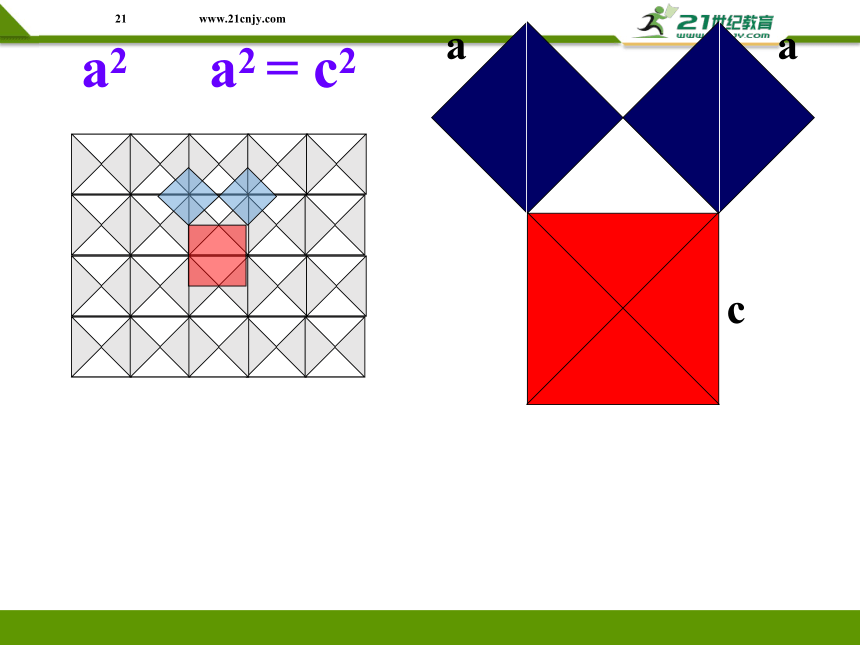
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面反映了直角三角形三边的某种数量关系。我们也来观察上图中的地面,看看能发现些什么。
毕达哥拉斯(公元前572—前492年)古希腊著名的哲学家、数学家、天文学家。
可以发现,以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积。即我们惊奇地发现,等腰直角三角形的三边之间有一种特殊的关系:斜边的平方等于两直角边的平方和。
a
a
c
a2 + a2 = c2
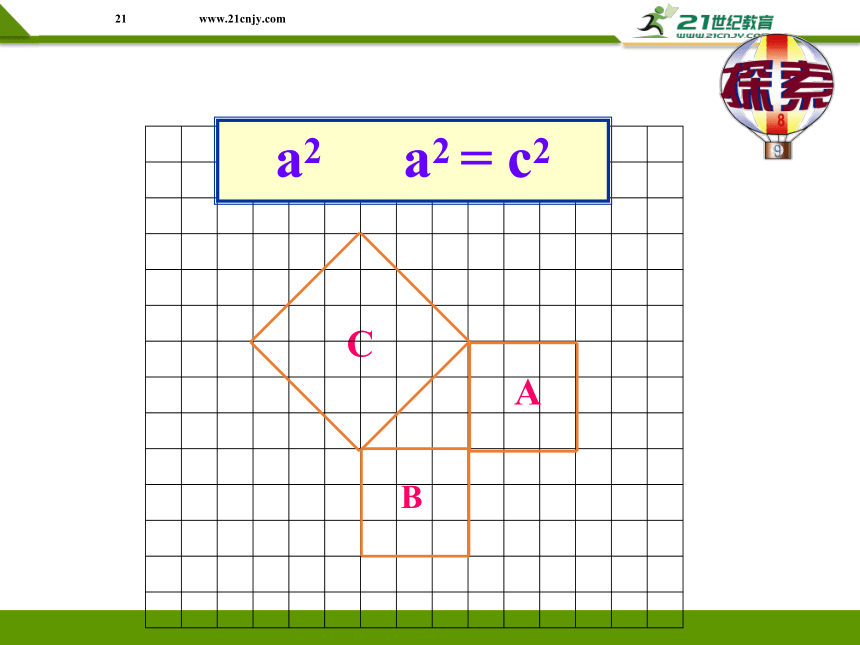
等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
B
C
A
(图中每个小方格代表一个单位面积)
a2 + a2 = c2
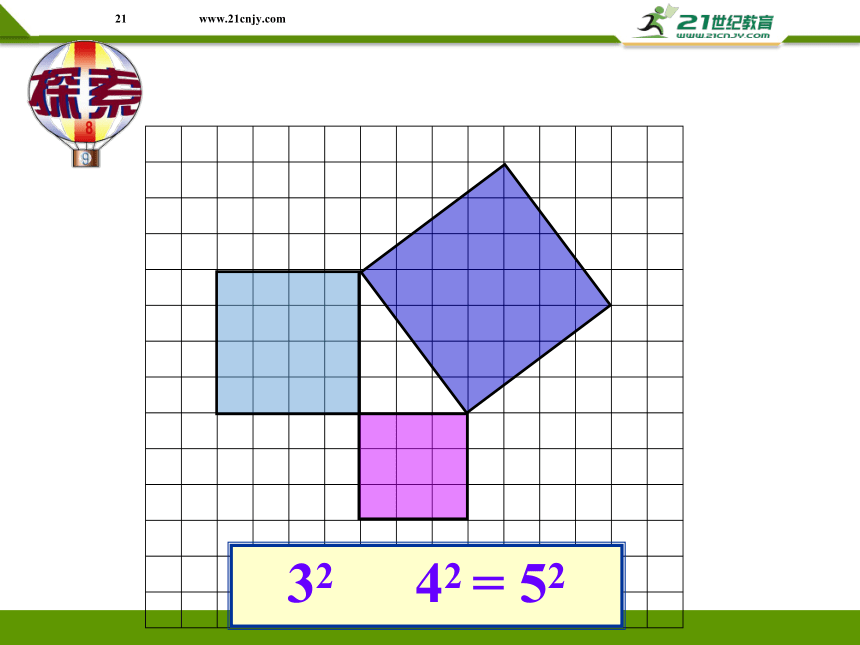
等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
32 + 42 = 52
伟大的猜想:
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2
命题1
勾股定理
这个定理是历时最长,研究的人最多,证明方法最多的一个定理,下面仅介绍我国古代赵爽的证法。
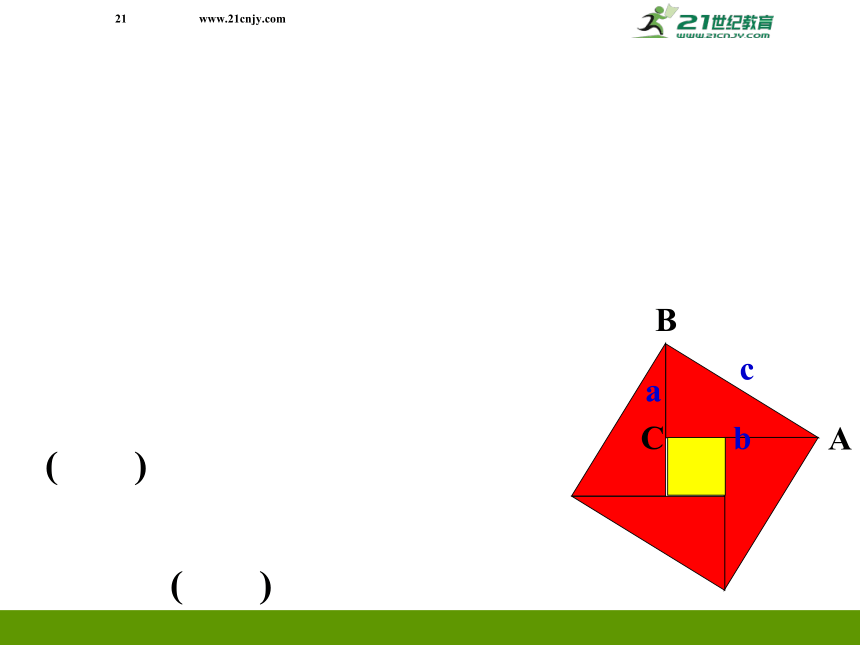
下边的图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”。赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四, 以勾股之差自相乘为中黄实。加差实,亦成弦实。
即 四个全等的直角三角形(红色)可以如图围成一个大正方形,中空的部分是一个小正方形 (黄色)。
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
赵爽证法的基本思路是:
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
⑴把边长为a,b的两个正方形连在一起
它们的面积和是 a2+b2
⑵再在边长为b的正方形内画边长为a的正方形,之后如图分割,则此时两直角三角形和弦图中的朱实全等,即它们的斜边为c。
b
a
c
c
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
b
a
c
c
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲。因此,这个图案被选为2002年北京召开的国际数学家大会的会微。
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
下面我们用现代数学公式进行证明:
边长为c的正方形的面积可用两种方法进行表示:
c2
或 4个直角三角形的面积+1个边长为(b-a)的小正方形的面积,即
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
下面我们用现代数学公式进行证明:
=c2
2ab+b2-2ab+a2=c2
a2+b2 = c2
在西方,一般认为这个定理是由毕达哥拉斯发现的所以人们称这个定理为毕达哥拉斯定理。
勾股定理 (或毕达哥拉斯定理)
勾股定理有广泛应用,下面我们用它探究几个问题
如果直角三角形两直角边分别为a,b,斜边为c,那么 a2+b2 = c2
直角三角形两直角边的平方和等于斜边的平方。
例1、一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
A
B
C
D
2m
1m
分析:可以看到,木板横着进,竖着进,都不能从门框内通过,只能试试斜着能否通过。对角线AC是斜着能通过的最大长度。求出AC,再与木板的宽比较,就能知道木板能否通过。
例1、一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
解:在Rt△ABC中,
根据勾股定理。
A
B
C
D
2m
1m
AC2=AB2+BC2
=12+22
=5
∴AC=
≈2.236
∵AC>木板的宽,∴木板能从门框内通过。
例2、如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
A
B
C
D
O
解:在Rt△AOB中,
OB2=AB2-AO2
=32-2.52
=2.75
∴ OB≈1.658
例2、如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
A
B
C
D
O
在Rt△COD中,
OD2=CD2-CO2
=32-(2.5-0.5)2
=5
∴ OD≈2.236
BD=OD-OB
=0.578
梯子底端B外移0.578m
1、有一个边长为50dm的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50
50
解:在Rt△ABC中,由勾股定理,得
A
B
C
AB2=BC2+AC2
=502+502
=5000
∴AB=
≈71
答:圆的直径至少71dm。
2、如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,你能求出A,B两点间的距离吗(结果保留整数)?
A
B
C
20
60
解:在Rt△ABC中,由勾股定理,得
AB2=BC2-AC2
=602-202
=3200
∴AB=
≈57
答: A,B两点间的距离是57m。
3、小明妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
3、小明妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
58cm
46cm
A
B
C
解:在Rt△ABC中,由勾股定理,得
AB2=BC2+AC2
=582+462
=5480
∴AB=
≈74
答:不同意他的想法,电视机的大小是
用对角线的长度(本机74厘米)来表示的。
4、若正方形的面积为2cm2,则它的对角线长是 .
5、 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .
6、8、10
6、如图,在Rt△ABC中,∠C=90°,∠B=22.5°AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE的长是 。
A
B
C
E
D
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
勾股定理
人教版 八年级下
在我国古代,人们将直角三角形中短的直角边叫做勾,长的直角边叫做股。斜边叫做弦。
据我国古算书《周髀算经》记载,约公元前1100年,人们已经知道,如果勾是三、股是四,那么弦是五。后来人们进一步发现并证明了直角三角形三边之间的关系:两条直角边的平方和等于斜边的平方。你能发现这个关系吗?
上面的图案有什么意义?为什么选它作为2002年在北京召开的国际数学家大会的会徽?
学过本章,你就能回答上述问题了。本章中,我们将探索直角三角形的三边之间特有的数量关系,并运用所得结论解决问题。
ICM 2002
Beijing
August 20-28. 2002
相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面反映了直角三角形三边的某种数量关系。我们也来观察上图中的地面,看看能发现些什么。
毕达哥拉斯(公元前572—前492年)古希腊著名的哲学家、数学家、天文学家。
可以发现,以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积。即我们惊奇地发现,等腰直角三角形的三边之间有一种特殊的关系:斜边的平方等于两直角边的平方和。
a
a
c
a2 + a2 = c2
等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
B
C
A
(图中每个小方格代表一个单位面积)
a2 + a2 = c2
等腰直角三角形有上述性质,其他的直角三角形也有这个性质吗?
32 + 42 = 52
伟大的猜想:
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2
命题1
勾股定理
这个定理是历时最长,研究的人最多,证明方法最多的一个定理,下面仅介绍我国古代赵爽的证法。
下边的图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”。赵爽指出:按弦图,又可以勾股相乘为朱实二,倍之为朱实四, 以勾股之差自相乘为中黄实。加差实,亦成弦实。
即 四个全等的直角三角形(红色)可以如图围成一个大正方形,中空的部分是一个小正方形 (黄色)。
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
赵爽证法的基本思路是:
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
⑴把边长为a,b的两个正方形连在一起
它们的面积和是 a2+b2
⑵再在边长为b的正方形内画边长为a的正方形,之后如图分割,则此时两直角三角形和弦图中的朱实全等,即它们的斜边为c。
b
a
c
c
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
b
a
c
c
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智,它是我国古代数学的骄傲。因此,这个图案被选为2002年北京召开的国际数学家大会的会微。
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
下面我们用现代数学公式进行证明:
边长为c的正方形的面积可用两种方法进行表示:
c2
或 4个直角三角形的面积+1个边长为(b-a)的小正方形的面积,即
朱实
朱实
朱实
朱实
A
B
C
b
c
a
黄实
下面我们用现代数学公式进行证明:
=c2
2ab+b2-2ab+a2=c2
a2+b2 = c2
在西方,一般认为这个定理是由毕达哥拉斯发现的所以人们称这个定理为毕达哥拉斯定理。
勾股定理 (或毕达哥拉斯定理)
勾股定理有广泛应用,下面我们用它探究几个问题
如果直角三角形两直角边分别为a,b,斜边为c,那么 a2+b2 = c2
直角三角形两直角边的平方和等于斜边的平方。
例1、一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
A
B
C
D
2m
1m
分析:可以看到,木板横着进,竖着进,都不能从门框内通过,只能试试斜着能否通过。对角线AC是斜着能通过的最大长度。求出AC,再与木板的宽比较,就能知道木板能否通过。
例1、一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
解:在Rt△ABC中,
根据勾股定理。
A
B
C
D
2m
1m
AC2=AB2+BC2
=12+22
=5
∴AC=
≈2.236
∵AC>木板的宽,∴木板能从门框内通过。
例2、如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
A
B
C
D
O
解:在Rt△AOB中,
OB2=AB2-AO2
=32-2.52
=2.75
∴ OB≈1.658
例2、如图,一个3m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.5m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
A
B
C
D
O
在Rt△COD中,
OD2=CD2-CO2
=32-(2.5-0.5)2
=5
∴ OD≈2.236
BD=OD-OB
=0.578
梯子底端B外移0.578m
1、有一个边长为50dm的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50
50
解:在Rt△ABC中,由勾股定理,得
A
B
C
AB2=BC2+AC2
=502+502
=5000
∴AB=
≈71
答:圆的直径至少71dm。
2、如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得CB=60m,AC=20m,你能求出A,B两点间的距离吗(结果保留整数)?
A
B
C
20
60
解:在Rt△ABC中,由勾股定理,得
AB2=BC2-AC2
=602-202
=3200
∴AB=
≈57
答: A,B两点间的距离是57m。
3、小明妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
3、小明妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
58cm
46cm
A
B
C
解:在Rt△ABC中,由勾股定理,得
AB2=BC2+AC2
=582+462
=5480
∴AB=
≈74
答:不同意他的想法,电视机的大小是
用对角线的长度(本机74厘米)来表示的。
4、若正方形的面积为2cm2,则它的对角线长是 .
5、 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .
6、8、10
6、如图,在Rt△ABC中,∠C=90°,∠B=22.5°AB的垂直平分线交AB于D,交BC于E,若CE=3,则BE的长是 。
A
B
C
E
D
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
