19.1.2函数的图象1(课件)
图片预览





文档简介
(共29张PPT)
19.1.2
函数的图象
有些问题中的函数关系很难列式表示,但是可以用图来直观地反映,例如用心电图表示心脏生物电流与时间的关系。即使对于能列式表示的函数关系,如能画图表示则会使函数关系更清晰。
函数的图象
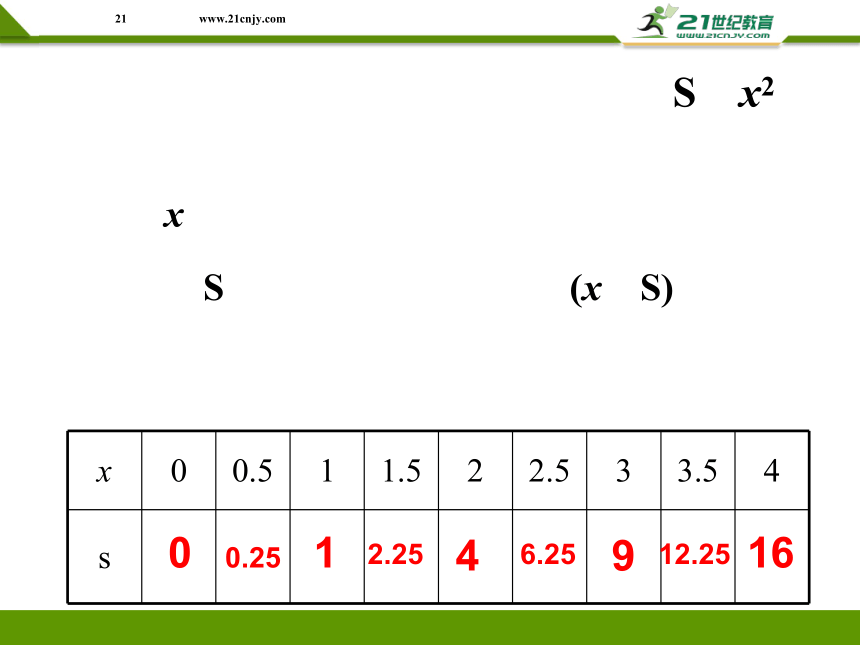
正方形的边长x与面积S的函数关系为: S=x2,其中自变量x的取值范围是x>0。我们还可以利用在坐标系中画图的方法来表示S与x的关系。
函数的图象
自变量x的一个确定的值与它们所对应的唯一的函数值S,是否确定了一个点(x,S)呢?计算并填写下表:
x 0 0.5 1 1.5 2 2.5 3 3.5 4
s
S=x2
0
0.25
1
2.25
4
6.25
9
12.25
16
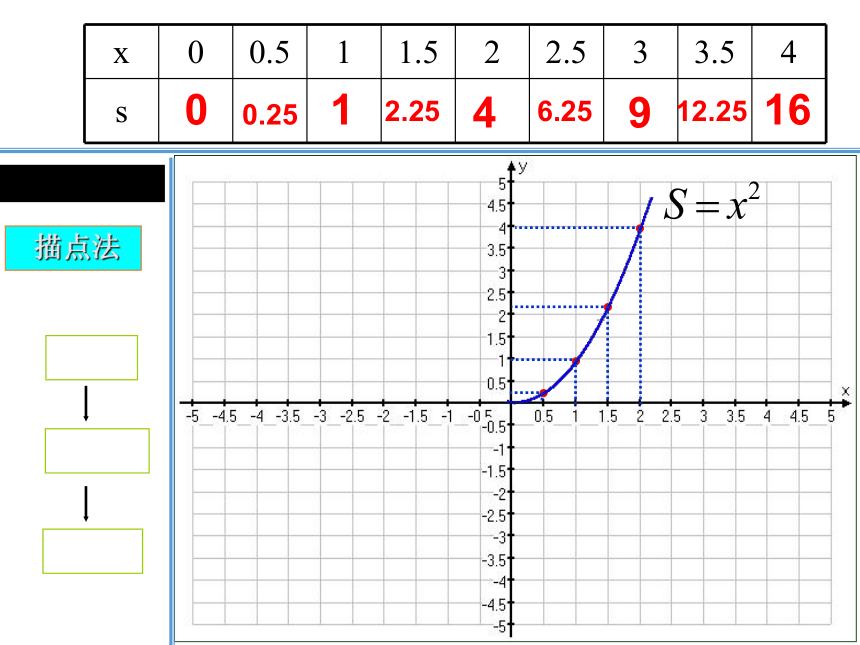
函数图象画法
列表
描点
连线
描点法
x 0 0.5 1 1.5 2 2.5 3 3.5 4
s
0
0.25
1
2.25
4
6.25
9
12.25
16
函数的图象
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象,上面的曲线就是函数 S=x2 (x>0) 的图象。
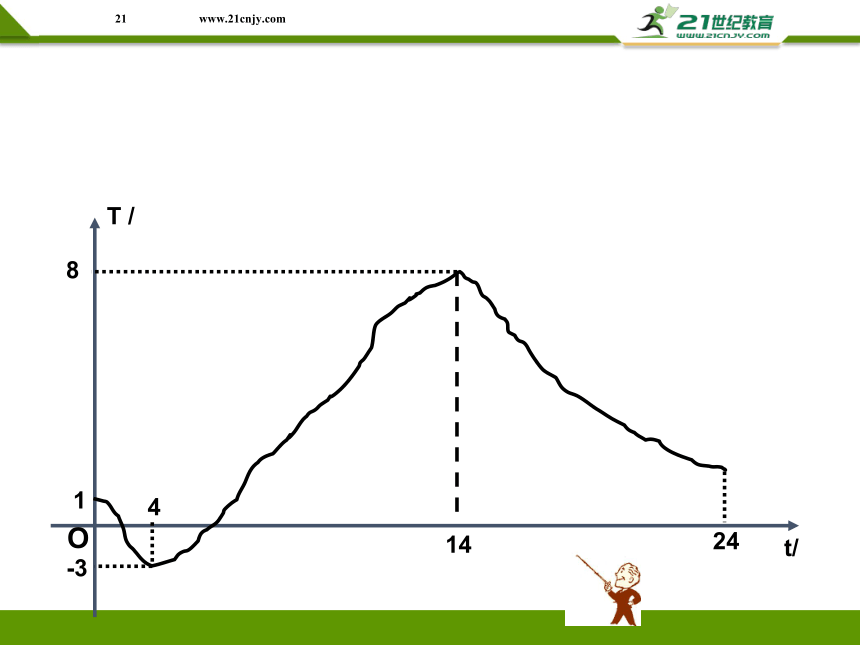
下图是自动测温仪记录的图象,它反映了北京的春季某天气温如何随时间的变化而变化,你从图象中得到了哪些信息?
O
-3
4
14
24
t/时
T /℃
8
1
可以认为,气温是时间的函数,图中是这个函数的图象,由图可知:
⑴ 这一天中凌晨4时气温最低(-3℃)
14时气温最高(8℃)
⑵ 从0时至4时气温呈下降状态(即温度随时间的增长而下降)从4时到14时气温呈上升状态,从14时至24时气温又呈下降状态。
⑶ 我们可以从图象中看出这一天中任一时刻的气温大约是多少;
⑷ 如果长期观察这样的气温,我们就能得到更多信息,掌握更多气温变化的规律。
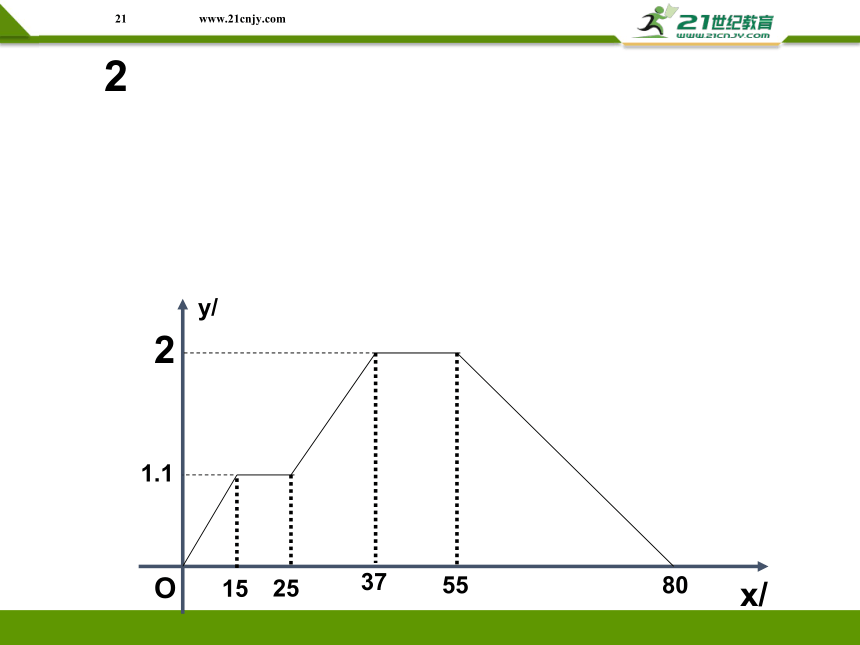
例2、下面的图象,反映的过程是:
小明从家去菜地浇水,又去玉米地锄草,然后回到家。其中表示时间,表示小明离他家的距离。
O
15
55
80
x/分
2
1.1
y/千米
25
37
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑴菜地离小明家多远 小明走到菜地用了多长时间
⑵小明给菜地浇水用了多长时间
⑶菜地离玉米地有多远 小明从菜地到玉米用了多少长时间
⑷小明给玉米地锄草用了多长时间
⑸玉米离小明家多远 小明从玉米地走回家的平均速度是多少
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑴菜地离小明家多远 小明走到菜地用了多长时间
解:⑴ 由纵坐标看出,菜地离小明家1.1千米 ;由横坐标看出,小明走到菜地用了15分。
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑵ 小明给菜地浇水用了多长时间
解:⑵ 由横坐标看出,小明给菜地浇水用了10分(即25-15)分。
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑶ 菜地离玉米地有多远 小明从菜地到玉米用了多少长时间
解:⑶ 由纵坐标看出,菜地离玉米地0.9(即2-1.1)千米;由横坐标看出,小明从菜地到玉米地用了12 (即37-25)分。
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑷小明给玉米地锄草用了多长时间
解:⑷ 由横坐标看出,小明给玉米地锄草用了18(即55-37)分。
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑸ 玉米地离小明家多远 小明从玉米地走回家的平均速度是多少
解:⑸ 由纵坐标看出,玉米地离小明家2千米;由横坐标看出,小明从玉米地走回家用了25 (即80-55)分,平均速度是0.08千米/分。
例3、在下列式子中,对于x的每一确定的值,y有唯一的对应值,即y是x的函数,画出这些函数的图象;
⑴ y=x+0.5 ⑵
(x>0)
解:⑴ y=x+0.5 x取任意实数式子都有意义,所以x的取值范围是全体实数。
从x的取值范围中选取一些数值,算出y的对应值,列表(计算并填写表中的空格)
x
y
0.5
0
1
1.5
2
-0.5
-1
0.5
1
1.5
2
-0.5
-1
2.5
列出 y=x+0.5 的x和y的对应值表:
x … -3 -2 -1 0 1 2 3 …
y=x+0.5 … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
根据表中的数值描点(x,y)并用平滑曲线连接这些点.
●
●
●
●
从图象可以看出, y=x+0.5图象是一条直线,且画出的直线从左向右上升,即当x由小变大时 y=x+0.5 随之增大。
⑵
解:列表→
x … 0.5 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 12 6 4 3 2.4 2 1.7 1.5 1.2 1 …
描点→
连线
根据表中的数值描点(x,y)并用平滑曲线连接这些点.
x
y
4
0
1
3
2
1
2
3
4
5
5
6
6
从图象可以看出,曲线不再是一条直线,且曲线由左向右下降,即当x由小变大时 y的值随之减小。
第一步:列表(表中给出一些自变量的值及其对应的函数值)。
第二步:描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点);
第三步:连线(按照横坐标由小到大的顺序把所描出的各点用平滑的曲线连接起来)。
描点法画图象的一般步骤如下:
⑴ 如图是一种古代计时器——“漏壶”的示意图,在壶内成盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间,用x表示时间,y表示壶底到水面的高度,下面的哪个图象适合表示一小段时间内y与x的函数关系(暂不考虑水量变化对压力的影响)
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
思考题
思考题
⑵a是自变量x取值内的任意一个值,过点(a,0)画y轴的平行线,与图中曲线相交,下列哪个图中的曲线表示y是x的函数?为什么?
x
y
a
o
x
y
a
o
答:⑵由于当x=a时y只能有唯一的对应值,所以函数图象与直线x=a只能有一个交点。本题应选左边的图象。
1、⑴画出函数y=2x-1的图象;
⑵判断点A(-2.5,-4),B(1,3),C(2.5,4)是否在函数y=2x-1的图象上。
x
y
o
-1
1
●
●
y=2x-1
答:只有点C在函数
y=2x-1的图象上。
⑴ 这一天内上海与北京何时温度相同?
2、下图是北京与上海在某一天的气温随时间变化的图象;
3
6
9
12
15
18
21
24
3
6
9
-3
O
T/℃
t/时
●
●
●
4
7
●
●
8
●
●
答:7时,12时温度相同。
上海
北京
⑵ 这一天内,上海在哪段时间内比北京的温度高?在哪段时间内比北京的温度低?
2、下图是北京与上海在某一天的气温随时间变化的图象;
3
6
9
12
15
18
21
24
3
6
9
-3
O
T/℃
t/时
●
●
●
4
7
●
●
8
●
●
答:0~7时,12~24时上海温度高。
上海
北京
7 ~12时上海比北京温度低。
3、⑴ 画出函数y=x2的图象;
⑵ 从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小?当x>0时呢?
①、列表:
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
②、描点:根据表中x,y的数值在坐
标平面中描点(x,y).
③、连线:用平滑曲线顺次连接各点,
就得到y=x2的图象.
3、⑴ 画出函数y=x2的图象;
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
x
y
0
0
0
1
1
2
4
3
9
-1
1
-2
4
-3
9
y=x2
●
●
●
●
●
●
●
⑵从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小?当x>0时呢?
答:① 当x<0时,y随x的增大而减小。
②当x>0时,y随x的增大而增大。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
19.1.2
函数的图象
有些问题中的函数关系很难列式表示,但是可以用图来直观地反映,例如用心电图表示心脏生物电流与时间的关系。即使对于能列式表示的函数关系,如能画图表示则会使函数关系更清晰。
函数的图象
正方形的边长x与面积S的函数关系为: S=x2,其中自变量x的取值范围是x>0。我们还可以利用在坐标系中画图的方法来表示S与x的关系。
函数的图象
自变量x的一个确定的值与它们所对应的唯一的函数值S,是否确定了一个点(x,S)呢?计算并填写下表:
x 0 0.5 1 1.5 2 2.5 3 3.5 4
s
S=x2
0
0.25
1
2.25
4
6.25
9
12.25
16
函数图象画法
列表
描点
连线
描点法
x 0 0.5 1 1.5 2 2.5 3 3.5 4
s
0
0.25
1
2.25
4
6.25
9
12.25
16
函数的图象
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象,上面的曲线就是函数 S=x2 (x>0) 的图象。
下图是自动测温仪记录的图象,它反映了北京的春季某天气温如何随时间的变化而变化,你从图象中得到了哪些信息?
O
-3
4
14
24
t/时
T /℃
8
1
可以认为,气温是时间的函数,图中是这个函数的图象,由图可知:
⑴ 这一天中凌晨4时气温最低(-3℃)
14时气温最高(8℃)
⑵ 从0时至4时气温呈下降状态(即温度随时间的增长而下降)从4时到14时气温呈上升状态,从14时至24时气温又呈下降状态。
⑶ 我们可以从图象中看出这一天中任一时刻的气温大约是多少;
⑷ 如果长期观察这样的气温,我们就能得到更多信息,掌握更多气温变化的规律。
例2、下面的图象,反映的过程是:
小明从家去菜地浇水,又去玉米地锄草,然后回到家。其中表示时间,表示小明离他家的距离。
O
15
55
80
x/分
2
1.1
y/千米
25
37
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑴菜地离小明家多远 小明走到菜地用了多长时间
⑵小明给菜地浇水用了多长时间
⑶菜地离玉米地有多远 小明从菜地到玉米用了多少长时间
⑷小明给玉米地锄草用了多长时间
⑸玉米离小明家多远 小明从玉米地走回家的平均速度是多少
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑴菜地离小明家多远 小明走到菜地用了多长时间
解:⑴ 由纵坐标看出,菜地离小明家1.1千米 ;由横坐标看出,小明走到菜地用了15分。
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑵ 小明给菜地浇水用了多长时间
解:⑵ 由横坐标看出,小明给菜地浇水用了10分(即25-15)分。
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑶ 菜地离玉米地有多远 小明从菜地到玉米用了多少长时间
解:⑶ 由纵坐标看出,菜地离玉米地0.9(即2-1.1)千米;由横坐标看出,小明从菜地到玉米地用了12 (即37-25)分。
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑷小明给玉米地锄草用了多长时间
解:⑷ 由横坐标看出,小明给玉米地锄草用了18(即55-37)分。
O
15
55
80
x/分
2
1.1
y/千米
25
37
根据图象回答问题:
⑸ 玉米地离小明家多远 小明从玉米地走回家的平均速度是多少
解:⑸ 由纵坐标看出,玉米地离小明家2千米;由横坐标看出,小明从玉米地走回家用了25 (即80-55)分,平均速度是0.08千米/分。
例3、在下列式子中,对于x的每一确定的值,y有唯一的对应值,即y是x的函数,画出这些函数的图象;
⑴ y=x+0.5 ⑵
(x>0)
解:⑴ y=x+0.5 x取任意实数式子都有意义,所以x的取值范围是全体实数。
从x的取值范围中选取一些数值,算出y的对应值,列表(计算并填写表中的空格)
x
y
0.5
0
1
1.5
2
-0.5
-1
0.5
1
1.5
2
-0.5
-1
2.5
列出 y=x+0.5 的x和y的对应值表:
x … -3 -2 -1 0 1 2 3 …
y=x+0.5 … -2.5 -1.5 -0.5 0.5 1.5 2.5 3.5 …
根据表中的数值描点(x,y)并用平滑曲线连接这些点.
●
●
●
●
从图象可以看出, y=x+0.5图象是一条直线,且画出的直线从左向右上升,即当x由小变大时 y=x+0.5 随之增大。
⑵
解:列表→
x … 0.5 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 12 6 4 3 2.4 2 1.7 1.5 1.2 1 …
描点→
连线
根据表中的数值描点(x,y)并用平滑曲线连接这些点.
x
y
4
0
1
3
2
1
2
3
4
5
5
6
6
从图象可以看出,曲线不再是一条直线,且曲线由左向右下降,即当x由小变大时 y的值随之减小。
第一步:列表(表中给出一些自变量的值及其对应的函数值)。
第二步:描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点);
第三步:连线(按照横坐标由小到大的顺序把所描出的各点用平滑的曲线连接起来)。
描点法画图象的一般步骤如下:
⑴ 如图是一种古代计时器——“漏壶”的示意图,在壶内成盛一定量的水,水从壶下的小孔漏出,壶壁内画出刻度,人们根据壶中水面的位置计算时间,用x表示时间,y表示壶底到水面的高度,下面的哪个图象适合表示一小段时间内y与x的函数关系(暂不考虑水量变化对压力的影响)
x
y
o
x
y
o
x
y
o
(A)
(B)
(C)
思考题
思考题
⑵a是自变量x取值内的任意一个值,过点(a,0)画y轴的平行线,与图中曲线相交,下列哪个图中的曲线表示y是x的函数?为什么?
x
y
a
o
x
y
a
o
答:⑵由于当x=a时y只能有唯一的对应值,所以函数图象与直线x=a只能有一个交点。本题应选左边的图象。
1、⑴画出函数y=2x-1的图象;
⑵判断点A(-2.5,-4),B(1,3),C(2.5,4)是否在函数y=2x-1的图象上。
x
y
o
-1
1
●
●
y=2x-1
答:只有点C在函数
y=2x-1的图象上。
⑴ 这一天内上海与北京何时温度相同?
2、下图是北京与上海在某一天的气温随时间变化的图象;
3
6
9
12
15
18
21
24
3
6
9
-3
O
T/℃
t/时
●
●
●
4
7
●
●
8
●
●
答:7时,12时温度相同。
上海
北京
⑵ 这一天内,上海在哪段时间内比北京的温度高?在哪段时间内比北京的温度低?
2、下图是北京与上海在某一天的气温随时间变化的图象;
3
6
9
12
15
18
21
24
3
6
9
-3
O
T/℃
t/时
●
●
●
4
7
●
●
8
●
●
答:0~7时,12~24时上海温度高。
上海
北京
7 ~12时上海比北京温度低。
3、⑴ 画出函数y=x2的图象;
⑵ 从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小?当x>0时呢?
①、列表:
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
②、描点:根据表中x,y的数值在坐
标平面中描点(x,y).
③、连线:用平滑曲线顺次连接各点,
就得到y=x2的图象.
3、⑴ 画出函数y=x2的图象;
x … -3 -2 -1 0 1 2 3 …
y=x2 … 9 4 1 0 1 4 9 …
x
y
0
0
0
1
1
2
4
3
9
-1
1
-2
4
-3
9
y=x2
●
●
●
●
●
●
●
⑵从图象中观察,当x<0时,y随x的增大而增大,还是y随x的增大而减小?当x>0时呢?
答:① 当x<0时,y随x的增大而减小。
②当x>0时,y随x的增大而增大。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
