19.1.2函数的图象2(课件)
图片预览







文档简介
(共24张PPT)
19.1.2函数的图象
人教版 八年级下
我们已经看到或亲自动手用列表格、写式子和画图象的方法表示了一些函数,这三种表示函数的方法分别称为:
⑴ 列表法;⑵ 解析式法;⑶ 图象法。
从前面的例子看,你认为三种表示函数的方法各有什么优点?
答:列表法直接给出部分函数值,解析法明显地表示对应规律,图象法明显地表示变化趋势。
表示函数时,要根据具体情况选择适当的方法来表示函数,有时为全面地认识问题,需要几种方法同时使用。
函数表示法的关系之一
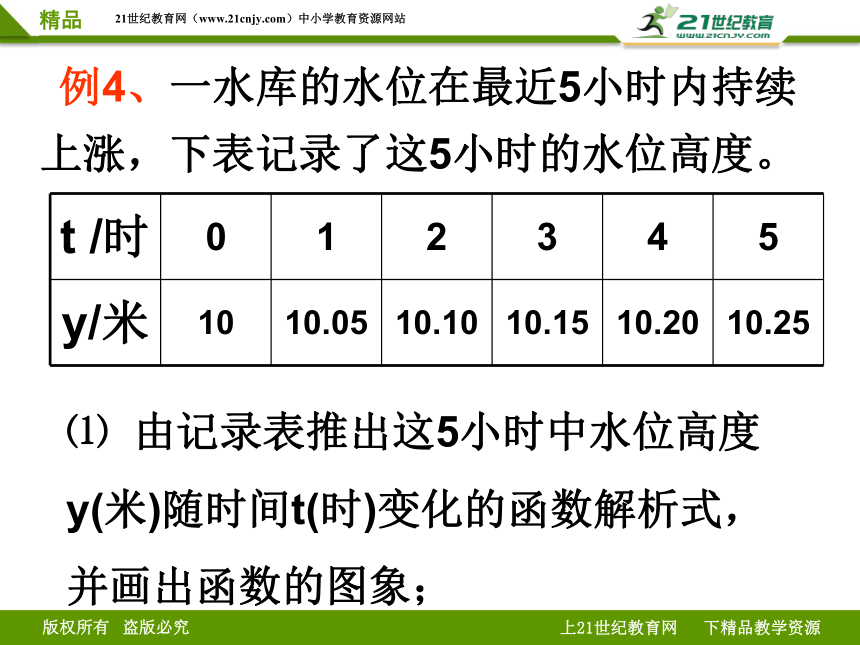
t /时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 10.25
例4、一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度。
⑴ 由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数的图象;
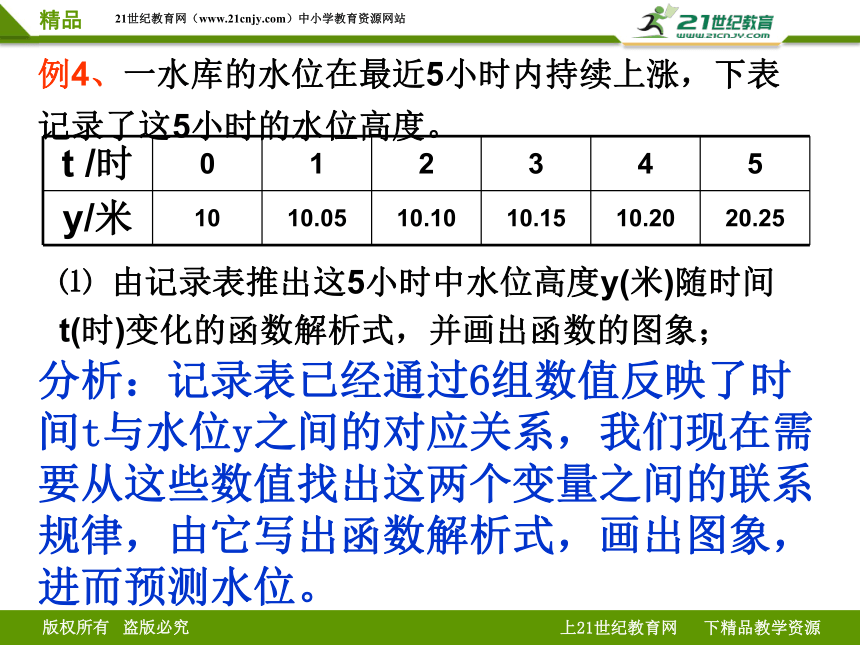
t /时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 20.25
例4、一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度。
⑴ 由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数的图象;
分析:记录表已经通过6组数值反映了时间t与水位y之间的对应关系,我们现在需要从这些数值找出这两个变量之间的联系规律,由它写出函数解析式,画出图象,进而预测水位。
t /时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 20.25
⑴ 由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数的图象;
解:由表中观察到开始水位高10米,以后每隔1小时,水位上升0.05米,这样的变化规律可以表示为:
y=0.05t+10
( 0≤t≤7 )
⑴ 由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数的图象;
解:由表中观察到开始水位高10米,以后每隔1小时,水位上升0.05米,这样的变化规律可以表示为:
y=0.05t+10
( 0≤t≤7 )
这个函数的图象如下图:
7
0
y
10
10.35
y=0.05t+10
t(时)
例4、一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度。
⑵ 据估计这种上涨的情况还会持续2小时,预测再过2小时水位高度将达到多少米?
解:⑵再过2小时的水位高度,就是:t=5+2=7时函数y=0.05t+10的值,从解析式容易算出:
y=0.05×7+10=10.35
从函数图象也能估出这个值是10.35米.
由例4可以看出函数的不同表示法之间可以互相转化,在对问题的研究中可从不同的侧面反映事物之间的内在联系。
函数表示法的关系之二
练习
1、用列表法与解析式法表示n边形的内角和m是边数n的函数。
解:解析式法: m=(n-2)×180
列表法:
n 3 4 5 6 7 ···
m° 180 360 540 720 900 ···
练习
2、用解析式法与图象法表示等边三角形的周长 l 是边长 a 的函数。
解:解析式法: l=3a
图象法:
1
0
l
3
l=3a
a
时间(分)
距离(米)
时间(分)
10 20 30 40 50
900
0
A
0
时间(分)
距离(米)
10 20 30 40 50
900
B
距离(米)
900
C
10 20 30 40 50
0
900
10 20 3 0 40 50
0
时间(分)
距离(米)
D
3、张大伯出去散步,从家走了20分钟,到了一个离家900米的阅报亭,看了10分钟报纸后,用了15分钟返回到家。下面哪个图象表示张大伯离家时间与距离之间的关系? ( )
D
6
2
O
x/时
y/微克
4、某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药的一定时间内每毫升血液中含药量y(微克)随时间x(时)逐步增加,变化情况如图所示.
⑴ 当x≤2时,y与x之间的函数关系式是 。
y=3x
6
2
O
x/时
y/微克
4⑵服药后2时,血液中含药量最高达每毫升6微克,接着每小时逐步衰减 微克。
求出当x≥2时 y 与 x 之间的函数关系式。
解:由题意可得
6
2
O
x/时
y/微克
4⑶ 如果每毫升血液中含药量4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长
4
6时
当 y=4 时
4=3x
当 y=4 时
5、某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示 .
y/升
x/分
0
40
4
15
根据图象解答下列问题:
洗衣机的进水时间是 分钟,
清洗时洗衣机中的水量是 升.
4
40
已知洗衣机的排水速度为每分钟19升,
①求排水时水量y与时间x之间的关系式。
y/升
x/分
0
40
4
15
解:由题意可得
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量。
y/升
x/分
0
40
4
15
17
2
解:当 x=15+2=17 分 时
=2
6、如图,矩形ABCD 中,AB=6cm,动点P从B出发,沿路径B→C→D→A移动.先以2㎝/s的速度由B→C→D移动 ,接着自D→A的移动速度变为1㎝/s,设相应的△ABP的面积为S,S关于时间t(单位:秒)的部分函数图象如图所示:
t/s
s/c㎡
0 5 8 12 16 20
t/s
s/c㎡
0 5 8 12 16 20
回答问题:(1)BC的长是 .
(2)图中 a = .
2cm/s
10cm
30
t/s
s/c㎡
0 5 8 12 16 20
回答问题:(1)BC的长是 .
(2)图中 = .
(3)补全P自D A时,相应的S 关于时间t的函数图象:
18
10cm
30
(4)写出(3)段的相应函数关系式.
1cm/s
在解决一次函数图象问题时,
2、注意认真理解题意,并和图象中的信息相结合,提高综合解题的能力。
1、关注图象中特定点表示的信息, 求出各段的表达式,从而理解整个过程.同时注意领悟数形结合的思想.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
19.1.2函数的图象
人教版 八年级下
我们已经看到或亲自动手用列表格、写式子和画图象的方法表示了一些函数,这三种表示函数的方法分别称为:
⑴ 列表法;⑵ 解析式法;⑶ 图象法。
从前面的例子看,你认为三种表示函数的方法各有什么优点?
答:列表法直接给出部分函数值,解析法明显地表示对应规律,图象法明显地表示变化趋势。
表示函数时,要根据具体情况选择适当的方法来表示函数,有时为全面地认识问题,需要几种方法同时使用。
函数表示法的关系之一
t /时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 10.25
例4、一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度。
⑴ 由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数的图象;
t /时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 20.25
例4、一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度。
⑴ 由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数的图象;
分析:记录表已经通过6组数值反映了时间t与水位y之间的对应关系,我们现在需要从这些数值找出这两个变量之间的联系规律,由它写出函数解析式,画出图象,进而预测水位。
t /时 0 1 2 3 4 5
y/米 10 10.05 10.10 10.15 10.20 20.25
⑴ 由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数的图象;
解:由表中观察到开始水位高10米,以后每隔1小时,水位上升0.05米,这样的变化规律可以表示为:
y=0.05t+10
( 0≤t≤7 )
⑴ 由记录表推出这5小时中水位高度y(米)随时间t(时)变化的函数解析式,并画出函数的图象;
解:由表中观察到开始水位高10米,以后每隔1小时,水位上升0.05米,这样的变化规律可以表示为:
y=0.05t+10
( 0≤t≤7 )
这个函数的图象如下图:
7
0
y
10
10.35
y=0.05t+10
t(时)
例4、一水库的水位在最近5小时内持续上涨,下表记录了这5小时的水位高度。
⑵ 据估计这种上涨的情况还会持续2小时,预测再过2小时水位高度将达到多少米?
解:⑵再过2小时的水位高度,就是:t=5+2=7时函数y=0.05t+10的值,从解析式容易算出:
y=0.05×7+10=10.35
从函数图象也能估出这个值是10.35米.
由例4可以看出函数的不同表示法之间可以互相转化,在对问题的研究中可从不同的侧面反映事物之间的内在联系。
函数表示法的关系之二
练习
1、用列表法与解析式法表示n边形的内角和m是边数n的函数。
解:解析式法: m=(n-2)×180
列表法:
n 3 4 5 6 7 ···
m° 180 360 540 720 900 ···
练习
2、用解析式法与图象法表示等边三角形的周长 l 是边长 a 的函数。
解:解析式法: l=3a
图象法:
1
0
l
3
l=3a
a
时间(分)
距离(米)
时间(分)
10 20 30 40 50
900
0
A
0
时间(分)
距离(米)
10 20 30 40 50
900
B
距离(米)
900
C
10 20 30 40 50
0
900
10 20 3 0 40 50
0
时间(分)
距离(米)
D
3、张大伯出去散步,从家走了20分钟,到了一个离家900米的阅报亭,看了10分钟报纸后,用了15分钟返回到家。下面哪个图象表示张大伯离家时间与距离之间的关系? ( )
D
6
2
O
x/时
y/微克
4、某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药的一定时间内每毫升血液中含药量y(微克)随时间x(时)逐步增加,变化情况如图所示.
⑴ 当x≤2时,y与x之间的函数关系式是 。
y=3x
6
2
O
x/时
y/微克
4⑵服药后2时,血液中含药量最高达每毫升6微克,接着每小时逐步衰减 微克。
求出当x≥2时 y 与 x 之间的函数关系式。
解:由题意可得
6
2
O
x/时
y/微克
4⑶ 如果每毫升血液中含药量4微克或4微克以上时在治疗疾病时是有效的,那么这个有效时间是多长
4
6时
当 y=4 时
4=3x
当 y=4 时
5、某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示 .
y/升
x/分
0
40
4
15
根据图象解答下列问题:
洗衣机的进水时间是 分钟,
清洗时洗衣机中的水量是 升.
4
40
已知洗衣机的排水速度为每分钟19升,
①求排水时水量y与时间x之间的关系式。
y/升
x/分
0
40
4
15
解:由题意可得
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量。
y/升
x/分
0
40
4
15
17
2
解:当 x=15+2=17 分 时
=2
6、如图,矩形ABCD 中,AB=6cm,动点P从B出发,沿路径B→C→D→A移动.先以2㎝/s的速度由B→C→D移动 ,接着自D→A的移动速度变为1㎝/s,设相应的△ABP的面积为S,S关于时间t(单位:秒)的部分函数图象如图所示:
t/s
s/c㎡
0 5 8 12 16 20
t/s
s/c㎡
0 5 8 12 16 20
回答问题:(1)BC的长是 .
(2)图中 a = .
2cm/s
10cm
30
t/s
s/c㎡
0 5 8 12 16 20
回答问题:(1)BC的长是 .
(2)图中 = .
(3)补全P自D A时,相应的S 关于时间t的函数图象:
18
10cm
30
(4)写出(3)段的相应函数关系式.
1cm/s
在解决一次函数图象问题时,
2、注意认真理解题意,并和图象中的信息相结合,提高综合解题的能力。
1、关注图象中特定点表示的信息, 求出各段的表达式,从而理解整个过程.同时注意领悟数形结合的思想.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
