19.1.2 函数的图象综合复习(课件)
图片预览









文档简介
(共46张PPT)
人教版 八年级下
一、函数的三种表示方法:
⑴ 列表法;⑵ 解析式法;⑶ 图象法。
答:列表法直接给出部分函数值;
解析法清楚地表示对应规律;
图象法直观地表示变化趋势。
表示函数时,要根据具体情况选择适当的方法来表示函数,有时为全面地认识问题,需要几种方法同时使用。
函数表示法的关系之一
二、为什么要用图象来表示函数?
答:因为有些问题中的函数关系很难列式表示,但是,可以用图像直观地反映。如用心电图表示心脏生物电流与时间的关系。即使对于能列式表示的函数关系,如能画图表示则会使函数关系更直观清晰。
⑴列表(表中给出一些自变量的值及其对应的函数值)。
⑵描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点);
⑶连线(按照横坐标由小到大的顺序把所描出的各点用平滑的曲线连接起来)。
三、描点法画图象的一般步骤:
四、点的坐标和解析式的关系
1、点P(m,n)在某函数的图象上,则该点的坐标代入函数的解析式中,左、右两边相等。(得方程)
2、点P(m,n)的坐标代入函数的解析式中,如果左、右两边相等,则该点在某函数的图象上。
五、函数图象与坐标轴的交点
⑴ 求当x=0时的函数值,
就是图象与y轴的交点。
⑵ 求当y=0时,x的值,
就是图象与x轴的交点。
六、正确读懂函数图象中的信息
在会画出函数图象的基础上,给出图象会正确读懂图象中的信息,并由此解决一些实际问题,例如由图象中的路程和时间数据求出平均速度等等。
综合练习题
一、填空题(共6道题)
1、描点法画函数图象有一般步骤是
⑴ ;
⑵ ;
⑶ 。
列表
描点
连线
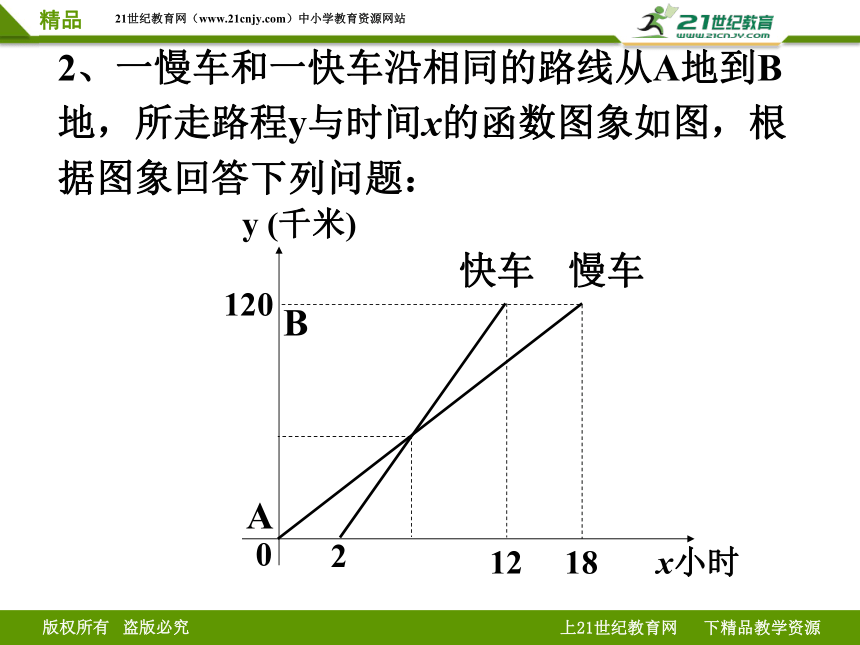
2、一慢车和一快车沿相同的路线从A地到B地,所走路程y与时间x的函数图象如图,根据图象回答下列问题:
A
B
120
y (千米)
2
12 18 x小时
快车
慢车
0
A
B
120
y (千米)
2
12 18 x小时
快车
慢车
0
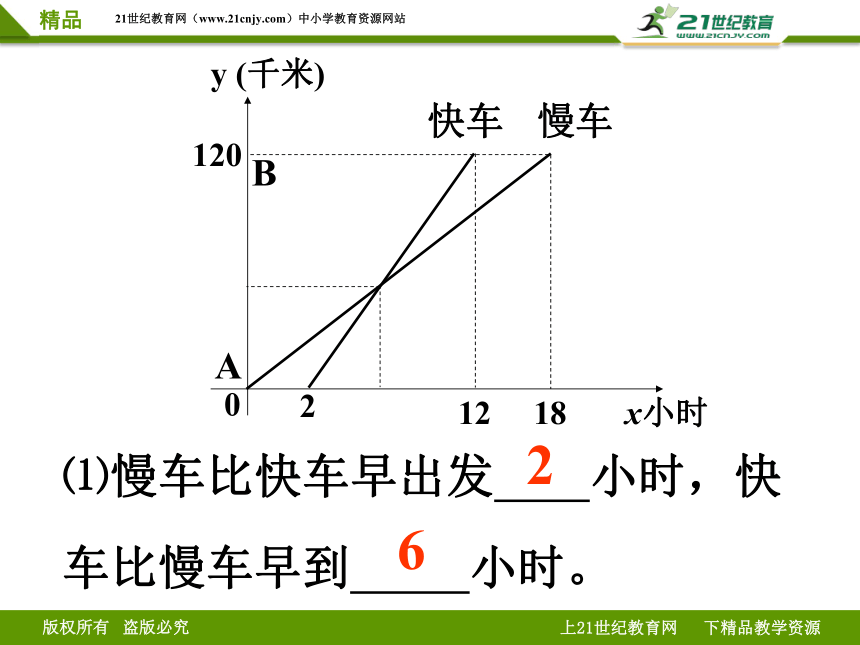
⑴慢车比快车早出发 小时,快车比慢车早到 小时。
2
6
A
B
120
y (千米)
2
12 18 x小时
快车
慢车
0
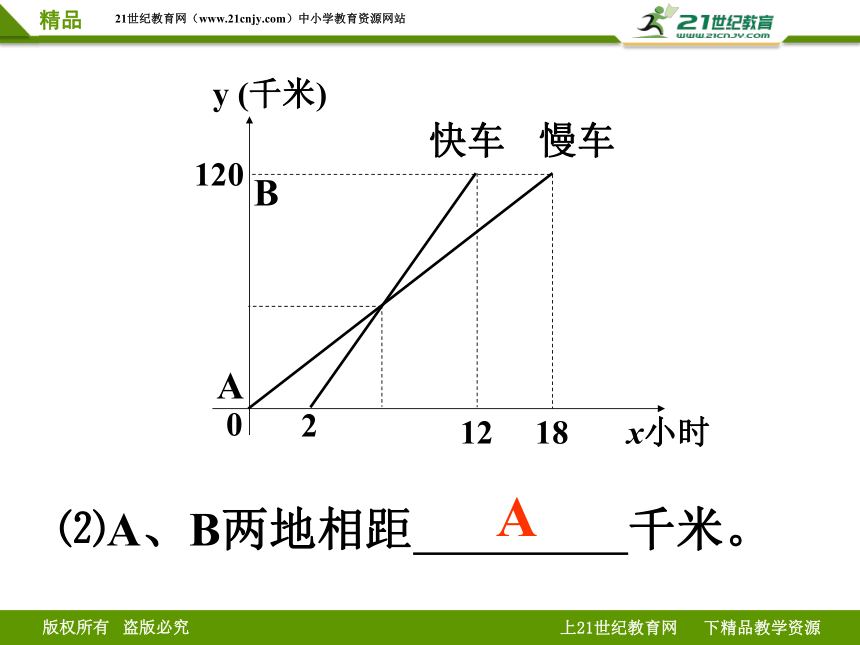
⑵A、B两地相距 千米。
A
3、若点A(2,4)在函数y=kx-2的
图象上,则k= 。
4=2k-2
k=3
3
4、求函数y=2x+6
与x轴的交点坐标是 ,
与y轴的交点坐标是 ,
解:当y=0时,
0=2x+6
x=-3
(-3,0)
当x=0时,
y=2×0+6
=6
(0,6)
5、某市自来水公司为了鼓励市民节约用水,采取分段收费标准,居民每月交水费y(元)与水量x(吨)的函数关系如图所示,请你通过观察函数图象,回答自来水公司收费标准:若用水不超过5吨,水费为 元/吨;超过部分的水费为 元/吨;
x(吨)
y(元)
0 5 8
7
13
1.4
2
6、设点P(3,m),Q(n,2)都在函数y=x-b的图象上,则m+n= 。
解:将P(3,m),Q(n,2)的坐标代入函数
的解析式中,得
m=3-b
2=n-b
n=b+2
m+n =3+2=5
5
7、函数y=2x-4的图象与x轴的交点A的坐标是 ,与y轴的交点B的坐标是 ,△AOB的面积是 。
(2,0)
(0,-4)
4
x
y
o
2
A
B
-4
8、如图表示某市2011年6月份某一天的气温随时间变化的情况。请观察此图,回答下列问题:
⑴这天的最高气温是 ℃;
⑵这天共有 小时的气温在31℃以上。
22
0 3 6 9 12 15 18 21 24
25
28
31
34
37
时间(时)
温度(℃)
37
●
9
9、如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系的图象,根据图象回答下列问题:
⑴当行驶8千米时,收费应为 元。
⑵从图象上你能获得哪些信息?(请写2条)
① ;
② 。
x(千米)
y(元)
5
11
3
8
O
⑶求出收费y(元)与行驶路程
x(千米)(x≥3)之间的函数关系式。
11
行驶3千米以内收费5元
行3千米以上1.2元/千米
二、选择题(共5道题)
1、下面【 】在函数
的图象上。
(A) (2,1) (B) (-2,1)
(C) (2,0) (D) (-2,0)
D
2、汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量y(升)与行驶的时间t(小时)的函数关系,用图象表示应为【 】
(A) (B) (C) (D)
40
8
0
t(h)
y(L)
40
8
0
t(h)
y(L)
40
8
0
t(h)
y(L)
40
8
0
t(h)
y(L)
B
3、一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶,过了一段时间,汽车到了下一个车站,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶,图中近似刻画出汽车在这段时间内的速度变化情况的是【 】
B
时间
0
速度
时间
0
速度
时间
0
速度
时间
0
速度
(A) (B) (C) (D)
4、向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面高度h与注水时间t之间的函数关系式大致是【 】
B
t
0
h
t
0
h
t
0
h
t
0
h
(A) (B) (C) (D)
5、如图,在边长为1的正方形ABCD的边上有一动点P,沿A→B→C→D→A运动一周,则P的纵坐标y与点P走过的路程S之间的函数关系用图象表示大致是【 】
D
P
A
B
C
D
●
1
2
1
2
x
y
0
y
0
2
4
1
2
S
(A)
(B)
(C)
(D)
y
0
2
4
1
2
S
y
0
2
4
1
2
S
y
0
2
4
1
2
S
6、某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)的关系如图所示,旅客可携带的免费行李的最大质量为【 】
A
(A)20kg (B)25kg (C) 28kg (D)30kg
0
y(元)
20 30 50
300
900
x(kg)
7、某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校。如图描述了他上学的情景,下列说法中错误的是【 】
0
离家的距离(米)
10 15 20
1000
离家时间(分)
2000
(A)修车时间15分;
(B)学校离家的距离为2000米;
(C)到达学校时共用时间20分钟;
(D)自行车发生故障时离家1000米。
A
8、在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止。设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图,则当x=9时,点R应运动到【 】
(A) N处;
(B) P处;
(C) Q处;
(D) M处。
M
N
P
Q
R
0
y
4 9
x
C
N
P
Q
M
9、由于干旱,某水库的蓄水量随时间的增加而直线下降。若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图,则下列说法正确的是【 】
(A) 干旱开始后,蓄水量每天减少20万米3 ;
(B) 干旱开始后,蓄水量每天增加20万米3 ;
(C)干旱开始时,蓄水量为200万米3 ;
(D)干旱第50天时,蓄水量为1200万米3。
A
1200
1000
800
600
400
200
V(万米3)
t(天)
10 20 30 40 50
o
10、★★小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图,下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别与上班时一致,则他从单位到家门口需要的时间是【 】
(A) 12分 ;
(B) 15分 ;
(C) 25分 ;
(D) 27分。
1
S(千米)
t(分)
3 8 12
o
2
4
A
B
单位
家
1
S(千米)
t(分)
3 8 12
o
2
4
A
B
单位
家
①从家走平路到A,
t=3分
②从A走上坡路到B,
S=2-1=1km
V=1÷(8-3)=0.2km/分
③从B走下坡路到单位,
S=4-2=2km
V=2÷(12-8)=0.5km/分
④从单位走上坡路到B,
t=2÷0.2=10 (分)
⑤从B走下坡路到A,
t=1÷0.5=2(分)
返回时共用时间:
T总=10+2+3=15(分)
10、★★小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图,下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别与上班时一致,则他从单位到家门口需要的时间是【 】
(A) 12分 ;
(B) 15分 ;
(C) 25分 ;
(D) 27分。
1
S(千米)
t(分)
3 8 12
o
2
4
A
B
单位
家
B
四、解答题(共5道题)
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑴小强到离家最远的地方需要几小时?此时离家多远?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
解:⑴小强到离家最远的地方需要3小时,此时离家30千米。
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑵ 何时开始第一次休息?休息时间多长?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
⑵ 离家1.5小时后开始第一次休息,休息0.5小时。
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑶ 返回时的平均速度是多少?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
⑶ 返回时的平均速度是:
30÷(6-4)
=15(km/h)
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑷ 小强何时距离家21千米?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
⑷ 设直线CD的解析式为:y=kx+b,则
2k+b=15
3k+b=30
k=15, b=-15
y=15x-15
当y=21时
15x-15=21
x=2.4
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑷ 小强何时距离家21千米?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
设直线EF的解析式为:y=mx+n,则
6m+n=0
4m+n=30
m=-15, n=90
y=-15x+90
当y=21时
-15x+90=21
x=4.6
2、汽车由天津驶往相距120千米的北京,S(千米)表示汽车离开天津的距离,t(小时)表示汽车行驶的时间,如图。
⑴汽车几小时可到达北京?速度是多少?
⑵汽车行驶1小时,离开天津有多远?
120
100
80
60
40
20
y(千米)
x(时)
1 2 3 4 5
0
2、汽车由天津驶往相距120千米的北京,S(千米)表示汽车离开天津的距离,t(小时)表示汽车行驶的时间,如图。
⑶当汽车距北京20千米时,汽车出发了
多长时间?
120
100
80
60
40
20
y(千米)
x(时)
1 2 3 4 5
0
3、甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系如图,根据图象回答问题:
⑴谁先出发?先出发多长时间?谁先到达终点?先到多长时间?
6
5
4
y(千米)
x(分)
5 10 15 20 25 30
0
甲
乙
3、甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系如图,根据图象回答问题:
⑵分别求出甲、乙两人的行驶速度?
6
5
4
y(千米)
x(分)
5 10 15 20 25 30
0
甲
乙
⑶在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):
6
5
4
y(千米)
x(分)
5 10 15 20 25 30
0
甲
乙
①甲在乙的前面;②甲与乙相遇;③甲在乙的后面。
4、一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售。售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:
⑴ 农民自带的零钱是多少?
答:农民自带的
零钱是5元。
x(千克)
y(元)
20
26
30
5
O
4、一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售。售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:
⑵降价前他每千克土豆出售的价格是多少?
答:(20-5)÷30
x(千克)
y(元)
20
26
30
5
O
=0.5(元)
4、一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:
⑶ 降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
(26-20)÷0.4+30
x(千克)
y(元)
20
26
30
5
O
=45(千克)
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
人教版 八年级下
一、函数的三种表示方法:
⑴ 列表法;⑵ 解析式法;⑶ 图象法。
答:列表法直接给出部分函数值;
解析法清楚地表示对应规律;
图象法直观地表示变化趋势。
表示函数时,要根据具体情况选择适当的方法来表示函数,有时为全面地认识问题,需要几种方法同时使用。
函数表示法的关系之一
二、为什么要用图象来表示函数?
答:因为有些问题中的函数关系很难列式表示,但是,可以用图像直观地反映。如用心电图表示心脏生物电流与时间的关系。即使对于能列式表示的函数关系,如能画图表示则会使函数关系更直观清晰。
⑴列表(表中给出一些自变量的值及其对应的函数值)。
⑵描点(在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点);
⑶连线(按照横坐标由小到大的顺序把所描出的各点用平滑的曲线连接起来)。
三、描点法画图象的一般步骤:
四、点的坐标和解析式的关系
1、点P(m,n)在某函数的图象上,则该点的坐标代入函数的解析式中,左、右两边相等。(得方程)
2、点P(m,n)的坐标代入函数的解析式中,如果左、右两边相等,则该点在某函数的图象上。
五、函数图象与坐标轴的交点
⑴ 求当x=0时的函数值,
就是图象与y轴的交点。
⑵ 求当y=0时,x的值,
就是图象与x轴的交点。
六、正确读懂函数图象中的信息
在会画出函数图象的基础上,给出图象会正确读懂图象中的信息,并由此解决一些实际问题,例如由图象中的路程和时间数据求出平均速度等等。
综合练习题
一、填空题(共6道题)
1、描点法画函数图象有一般步骤是
⑴ ;
⑵ ;
⑶ 。
列表
描点
连线
2、一慢车和一快车沿相同的路线从A地到B地,所走路程y与时间x的函数图象如图,根据图象回答下列问题:
A
B
120
y (千米)
2
12 18 x小时
快车
慢车
0
A
B
120
y (千米)
2
12 18 x小时
快车
慢车
0
⑴慢车比快车早出发 小时,快车比慢车早到 小时。
2
6
A
B
120
y (千米)
2
12 18 x小时
快车
慢车
0
⑵A、B两地相距 千米。
A
3、若点A(2,4)在函数y=kx-2的
图象上,则k= 。
4=2k-2
k=3
3
4、求函数y=2x+6
与x轴的交点坐标是 ,
与y轴的交点坐标是 ,
解:当y=0时,
0=2x+6
x=-3
(-3,0)
当x=0时,
y=2×0+6
=6
(0,6)
5、某市自来水公司为了鼓励市民节约用水,采取分段收费标准,居民每月交水费y(元)与水量x(吨)的函数关系如图所示,请你通过观察函数图象,回答自来水公司收费标准:若用水不超过5吨,水费为 元/吨;超过部分的水费为 元/吨;
x(吨)
y(元)
0 5 8
7
13
1.4
2
6、设点P(3,m),Q(n,2)都在函数y=x-b的图象上,则m+n= 。
解:将P(3,m),Q(n,2)的坐标代入函数
的解析式中,得
m=3-b
2=n-b
n=b+2
m+n =3+2=5
5
7、函数y=2x-4的图象与x轴的交点A的坐标是 ,与y轴的交点B的坐标是 ,△AOB的面积是 。
(2,0)
(0,-4)
4
x
y
o
2
A
B
-4
8、如图表示某市2011年6月份某一天的气温随时间变化的情况。请观察此图,回答下列问题:
⑴这天的最高气温是 ℃;
⑵这天共有 小时的气温在31℃以上。
22
0 3 6 9 12 15 18 21 24
25
28
31
34
37
时间(时)
温度(℃)
37
●
9
9、如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系的图象,根据图象回答下列问题:
⑴当行驶8千米时,收费应为 元。
⑵从图象上你能获得哪些信息?(请写2条)
① ;
② 。
x(千米)
y(元)
5
11
3
8
O
⑶求出收费y(元)与行驶路程
x(千米)(x≥3)之间的函数关系式。
11
行驶3千米以内收费5元
行3千米以上1.2元/千米
二、选择题(共5道题)
1、下面【 】在函数
的图象上。
(A) (2,1) (B) (-2,1)
(C) (2,0) (D) (-2,0)
D
2、汽车开始行驶时,油箱内有油40升,如果每小时耗油5升,则油箱内的余油量y(升)与行驶的时间t(小时)的函数关系,用图象表示应为【 】
(A) (B) (C) (D)
40
8
0
t(h)
y(L)
40
8
0
t(h)
y(L)
40
8
0
t(h)
y(L)
40
8
0
t(h)
y(L)
B
3、一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶,过了一段时间,汽车到了下一个车站,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶,图中近似刻画出汽车在这段时间内的速度变化情况的是【 】
B
时间
0
速度
时间
0
速度
时间
0
速度
时间
0
速度
(A) (B) (C) (D)
4、向放在水槽底部的烧杯注水(流量一定),注满烧杯后,继续注水,直至注满水槽,水槽中水面高度h与注水时间t之间的函数关系式大致是【 】
B
t
0
h
t
0
h
t
0
h
t
0
h
(A) (B) (C) (D)
5、如图,在边长为1的正方形ABCD的边上有一动点P,沿A→B→C→D→A运动一周,则P的纵坐标y与点P走过的路程S之间的函数关系用图象表示大致是【 】
D
P
A
B
C
D
●
1
2
1
2
x
y
0
y
0
2
4
1
2
S
(A)
(B)
(C)
(D)
y
0
2
4
1
2
S
y
0
2
4
1
2
S
y
0
2
4
1
2
S
6、某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)的关系如图所示,旅客可携带的免费行李的最大质量为【 】
A
(A)20kg (B)25kg (C) 28kg (D)30kg
0
y(元)
20 30 50
300
900
x(kg)
7、某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校。如图描述了他上学的情景,下列说法中错误的是【 】
0
离家的距离(米)
10 15 20
1000
离家时间(分)
2000
(A)修车时间15分;
(B)学校离家的距离为2000米;
(C)到达学校时共用时间20分钟;
(D)自行车发生故障时离家1000米。
A
8、在长方形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止。设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图,则当x=9时,点R应运动到【 】
(A) N处;
(B) P处;
(C) Q处;
(D) M处。
M
N
P
Q
R
0
y
4 9
x
C
N
P
Q
M
9、由于干旱,某水库的蓄水量随时间的增加而直线下降。若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图,则下列说法正确的是【 】
(A) 干旱开始后,蓄水量每天减少20万米3 ;
(B) 干旱开始后,蓄水量每天增加20万米3 ;
(C)干旱开始时,蓄水量为200万米3 ;
(D)干旱第50天时,蓄水量为1200万米3。
A
1200
1000
800
600
400
200
V(万米3)
t(天)
10 20 30 40 50
o
10、★★小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图,下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别与上班时一致,则他从单位到家门口需要的时间是【 】
(A) 12分 ;
(B) 15分 ;
(C) 25分 ;
(D) 27分。
1
S(千米)
t(分)
3 8 12
o
2
4
A
B
单位
家
1
S(千米)
t(分)
3 8 12
o
2
4
A
B
单位
家
①从家走平路到A,
t=3分
②从A走上坡路到B,
S=2-1=1km
V=1÷(8-3)=0.2km/分
③从B走下坡路到单位,
S=4-2=2km
V=2÷(12-8)=0.5km/分
④从单位走上坡路到B,
t=2÷0.2=10 (分)
⑤从B走下坡路到A,
t=1÷0.5=2(分)
返回时共用时间:
T总=10+2+3=15(分)
10、★★小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图,下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别与上班时一致,则他从单位到家门口需要的时间是【 】
(A) 12分 ;
(B) 15分 ;
(C) 25分 ;
(D) 27分。
1
S(千米)
t(分)
3 8 12
o
2
4
A
B
单位
家
B
四、解答题(共5道题)
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑴小强到离家最远的地方需要几小时?此时离家多远?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
解:⑴小强到离家最远的地方需要3小时,此时离家30千米。
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑵ 何时开始第一次休息?休息时间多长?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
⑵ 离家1.5小时后开始第一次休息,休息0.5小时。
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑶ 返回时的平均速度是多少?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
⑶ 返回时的平均速度是:
30÷(6-4)
=15(km/h)
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑷ 小强何时距离家21千米?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
⑷ 设直线CD的解析式为:y=kx+b,则
2k+b=15
3k+b=30
k=15, b=-15
y=15x-15
当y=21时
15x-15=21
x=2.4
1、小强骑自行车去郊游,如图表示他离家的距离y千米与所用时间小时之间关系的函数图象,小强9点离开家,15点回家。根据这个图象,请你回答下列问题:
⑷ 小强何时距离家21千米?
30
25
20
15
10
5
y(千米)
x(时)
1 2 3 4 5 6
0
A
B
C
D
E
F
设直线EF的解析式为:y=mx+n,则
6m+n=0
4m+n=30
m=-15, n=90
y=-15x+90
当y=21时
-15x+90=21
x=4.6
2、汽车由天津驶往相距120千米的北京,S(千米)表示汽车离开天津的距离,t(小时)表示汽车行驶的时间,如图。
⑴汽车几小时可到达北京?速度是多少?
⑵汽车行驶1小时,离开天津有多远?
120
100
80
60
40
20
y(千米)
x(时)
1 2 3 4 5
0
2、汽车由天津驶往相距120千米的北京,S(千米)表示汽车离开天津的距离,t(小时)表示汽车行驶的时间,如图。
⑶当汽车距北京20千米时,汽车出发了
多长时间?
120
100
80
60
40
20
y(千米)
x(时)
1 2 3 4 5
0
3、甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系如图,根据图象回答问题:
⑴谁先出发?先出发多长时间?谁先到达终点?先到多长时间?
6
5
4
y(千米)
x(分)
5 10 15 20 25 30
0
甲
乙
3、甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系如图,根据图象回答问题:
⑵分别求出甲、乙两人的行驶速度?
6
5
4
y(千米)
x(分)
5 10 15 20 25 30
0
甲
乙
⑶在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):
6
5
4
y(千米)
x(分)
5 10 15 20 25 30
0
甲
乙
①甲在乙的前面;②甲与乙相遇;③甲在乙的后面。
4、一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售。售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:
⑴ 农民自带的零钱是多少?
答:农民自带的
零钱是5元。
x(千克)
y(元)
20
26
30
5
O
4、一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售。售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:
⑵降价前他每千克土豆出售的价格是多少?
答:(20-5)÷30
x(千克)
y(元)
20
26
30
5
O
=0.5(元)
4、一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图象回答下列问题:
⑶ 降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
(26-20)÷0.4+30
x(千克)
y(元)
20
26
30
5
O
=45(千克)
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
