19.2一次函数中考实战(优秀课件)
图片预览








文档简介
(共34张PPT)
人教版 八年级下
温故知新
1、什么是一次函数?什么是正比例函数?
答:① y=kx+b (k、b为常数,k≠0)
则称y是 x 的一次函数。
② y=kx ( k≠0 ) 称y是 x 的正比例函数。
正比例函数是一次函数,一 次函数不一定是正比例函数,正比例函数是一次函数的特殊情况。
2、一次函数y=kx+b (k≠0)有什么性质?
其中k、b在图象中所起的作用是什么?
② k在图象中决定倾斜方向和倾斜程度,k值相同的直线互相平行;而b是图象与 y 轴的交点, b值相同的直线交 y 轴于同一点。
答:①当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小。
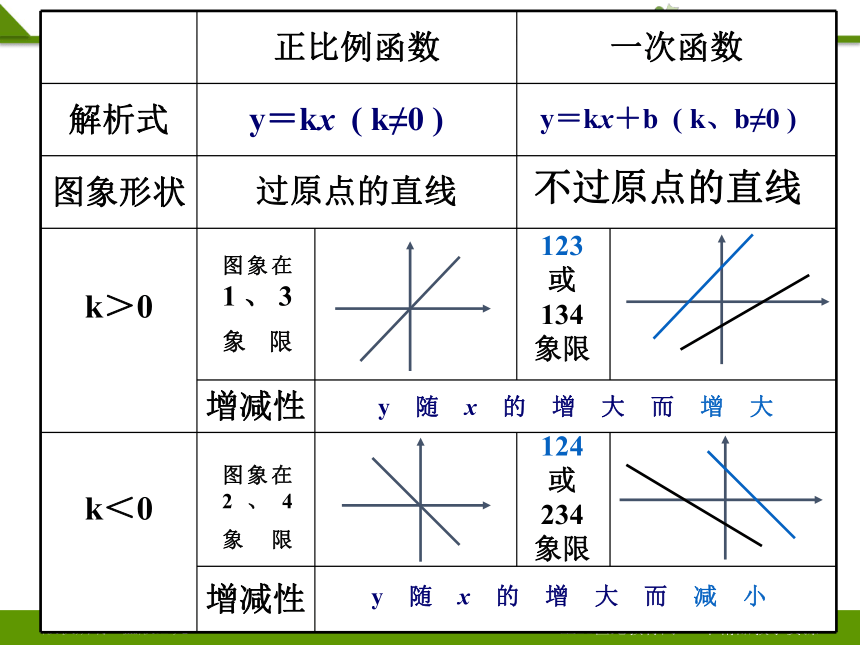
正比例函数 一次函数
解析式
图象形状
k>0
增减性
k<0
增减性
y=kx ( k≠0 )
y=kx+b ( k、b≠0 )
过原点的直线
不过原点的直线
图象在1、3
象限
y随x的增大而增大
y随x的增大而减小
123或134象限
图象在2、4
象限
124或234象限
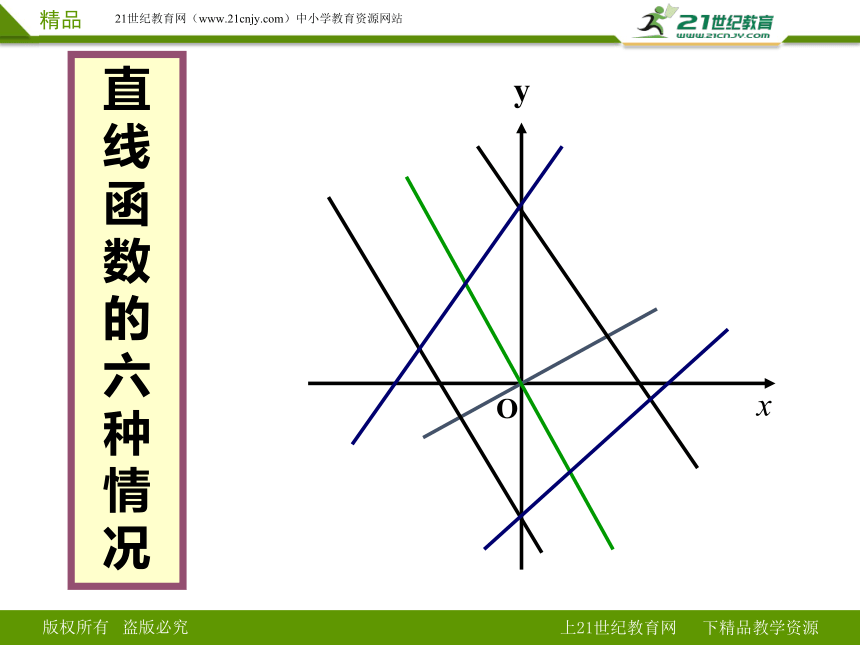
直线函数的六种情况
x
y
O
练习本准备好了吗?
Let’s begin!
一、选择题
1、在一次函数y=kx+3中,当x=3时,y=6,则k的值为( )
A、-1 B、1
C、5 D、-5
2、已知y是x的正比例函数,如果当x=4时,y=2,那么x=3时,y=( )
A、 B、2 C、3 D、6
一、选择题
2、直线y=kx+b在坐标系中的位
置如图,则( )
-1
-2
x
y
0
(A) k=-2, b=-1
(B) k=-0.5, b=-1
(C) k=-1, b=-2
(D) k=-1, b=-0.5
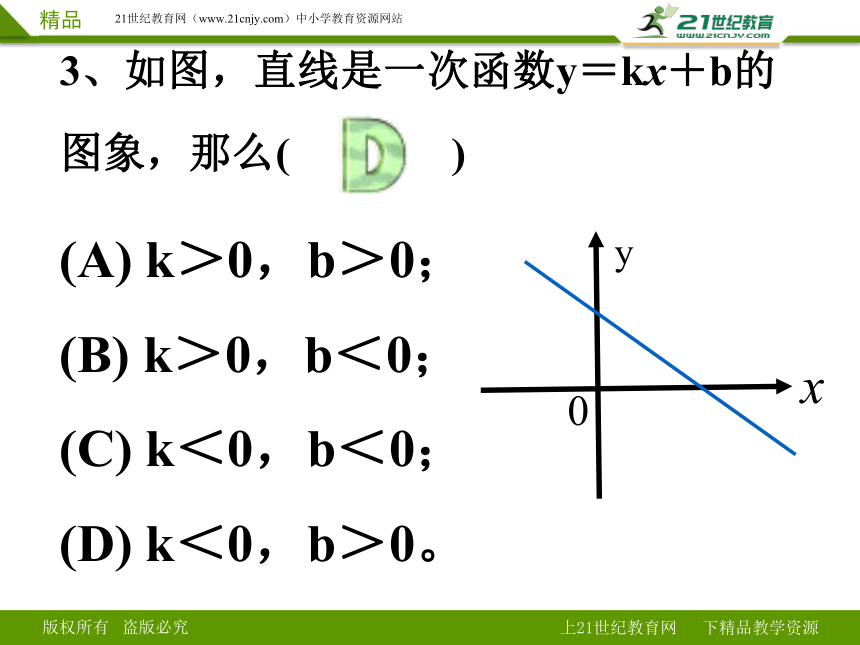
3、如图,直线是一次函数y=kx+b的图象,那么( )
(A) k>0,b>0;
(B) k>0,b<0;
(C) k<0,b<0;
(D) k<0,b>0。
x
y
0
4、下列说法中不正确的是( )
A、在函数y=2x+1中,y是x的正比例函数;
B、在 中, y是x的正比例函数;
C、在 xy=3 中,y与 成正比例;
D、在圆面积公式S=πR2中,S与R2成正比例
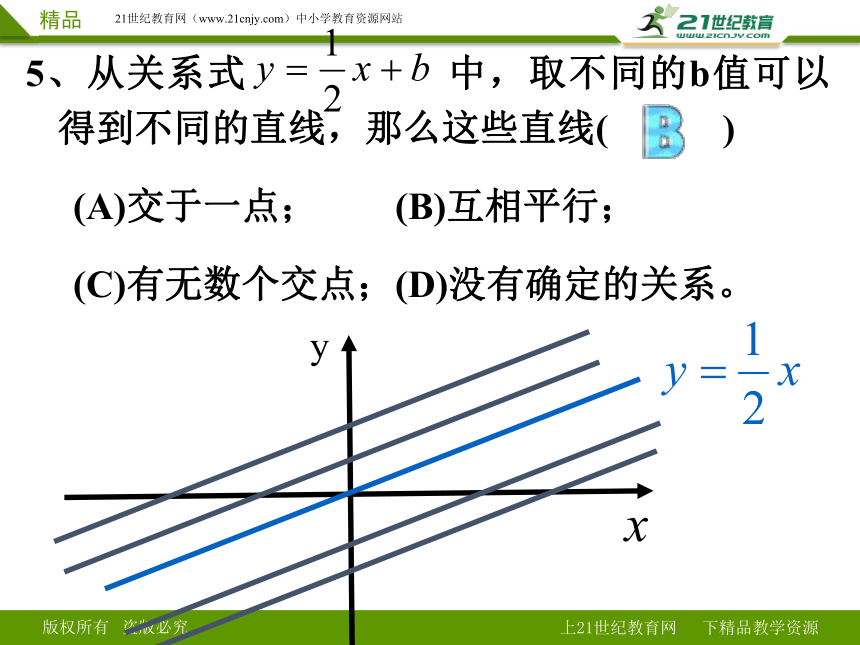
5、从关系式 中,取不同的b值可以得到不同的直线,那么这些直线( )
(A)交于一点; (B)互相平行;
(C)有无数个交点;(D)没有确定的关系。
x
y
6、已知y是x的正比例函数,若y随x增大而减小,且经过点A(3,-a),B(a,-1)两点,那么函数的解析式是( )
(A) ; (B)
(C) ; (D)
7、已知正比例函数y=(3k—1)x,若 y 随x的增大而增大,则k的取值范围是( )
A k<0 B k> 0
C k < D k>
D
3k-1>0
8、若一次函数y=kx-b 满足kb>0且函数值随着x的值的减小而增大,则它的大致图象是( )
y
x
0
y
x
0
y
x
0
y
x
0
(A)
(B)
(C)
(D)
1、若一次函数y=mx-(4m-3)的
图象过原点,则 m= ,若经过
点(0,5),则m= 。
(共6道题)
2、已知y=kx+b的图象上的点
在一、三、四象限内,
则k 0,b 0。
x
y
0
>
<
3、若一次函数的图象经过点A (3,1)
且过点(0,-3),则它的函数关系式
为y= 。
4、已知函数
k为 时,函数是正比例函数,其图象过 象限。函数值y随x的增大而 。
二、四
减小
5、把直线 y=3x 沿 轴
向 .平移2个单位,就得到直线y=3x+2。
x
y
0
y=3x
y=3x+2
2
●
上
6、若一次函数y1=kx+b的图象经过一、二、四象限,则一次函数y2=bx+k的图象经过 象限。
x
y
0
y1=kx+b
y2=bx+k
k<0
b>0
k<0
b>0
一、三、四
(7道题)
1、一次函数y=k1x-4与正比例函数
y=k2x 的图象都经过(2,-1)
①分别求出两个函数的解析式;
②求这两个函数的图象与x轴围成的三角形的面积。
解:①把x=2,y=-1代入两个函数中
-1=2k1-4
-1=2k2
答:两个函数分别是
1、一次函数y=k1x-4与正比例函数
y=k2x 的图象都经过(2,-1)
②求这两个函数的图象与x轴围成的三角形的面积。
解:②画出两个函数图象的草图
0
A
B
x
y
先求直线 与x轴的交点A
1、一次函数y=k1x-4与正比例函数
y=k2x 的图象都经过(2,-1)
②求这两个函数的图象与x轴围成的三角形的面积。
解:②如图画出两个函数的图象
0
A
B
x
y
再求两直线的交点B的坐标
C
└
2、已知函数y=-5xa+b+a-b是正比例函数,求 a-2b 的 值 .
解:由题意可得
a-b=0
∴ a =b
同时有 a+b=1
b+b=1
2b=1
3、如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在的直线为坐标轴建立直角坐标系,使D、A分别在 x 轴、y轴的正半轴上。
(1)求直线AC的解析式;
(2)若EC⊥AC于C,交x 轴于点E,连结AE。
x
y
A
B
C
D
E
0
1
2
┍
F
求证:∠1=∠2
3、如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在的直线为坐标轴建立直角坐标系,使D、A分别在 x 轴、y轴的正半轴上。
(1)求直线AC的解析式;
x
y
A
B
C
D
E
0
1
2
┍
F
解:设直线AC的解析式为:
y=kx+b
将A(0,2),C(2,1)
3、如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在的直线为坐标轴建立直角坐标系,使D、A分别在 x 轴、y轴的正半轴上。
(2)若EC⊥AC于C,交x 轴于点E,
x
y
A
B
C
D
E
0
1
2
┍
F
连结AE。求证:∠1=∠2
4、小芳的存折上已经有500元存款了,从现在开始她每个月可以得到150元的零用钱,小芳计划每月将零用钱的60%存入银行,用以购买她期盼已久的CD随身听(价值1680元)
(1)列出小芳的银行存款(不计利息)
y(元)与月数x 的函数关系式;
(2)多长时间以后,小芳的银行存款才能买随身听?
Y=500+150×60%·x
1680=500+150×60%·x
x≈13.1
答:14个月,小芳的银行存款才能买随身听。
5、已知一次函数y=(p+3)x+(2-q)
(1)p为什么实数时,y随x的增大而增大;
(2)q为什么实数时,函数的图象与y轴的交点在x轴上方;
(3)p、q为什么实数时,函数的图象过原点。
p+3>0
∴ p>- 3
p+3≠0且2-q>0
p+3≠0且2-q=0
6、某自行车保管站在某个星期日接受保管的自行车共有3500辆次,其中变速车保管费是每辆一次0.5元,一般车保管费是每辆一次0.3元。
(1)若设一般车停放的辆次为x,总的保管费收入为y(元),试写出y关于x的函数关系式。
(2)若估计停放的3500辆次自行车中,变速车的辆次不小于25%,不大于40%,试求该保管站这个星期日收入保管费总数的范围。
y=- 0.2x+1750
1225≤x≤1330
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
人教版 八年级下
温故知新
1、什么是一次函数?什么是正比例函数?
答:① y=kx+b (k、b为常数,k≠0)
则称y是 x 的一次函数。
② y=kx ( k≠0 ) 称y是 x 的正比例函数。
正比例函数是一次函数,一 次函数不一定是正比例函数,正比例函数是一次函数的特殊情况。
2、一次函数y=kx+b (k≠0)有什么性质?
其中k、b在图象中所起的作用是什么?
② k在图象中决定倾斜方向和倾斜程度,k值相同的直线互相平行;而b是图象与 y 轴的交点, b值相同的直线交 y 轴于同一点。
答:①当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小。
正比例函数 一次函数
解析式
图象形状
k>0
增减性
k<0
增减性
y=kx ( k≠0 )
y=kx+b ( k、b≠0 )
过原点的直线
不过原点的直线
图象在1、3
象限
y随x的增大而增大
y随x的增大而减小
123或134象限
图象在2、4
象限
124或234象限
直线函数的六种情况
x
y
O
练习本准备好了吗?
Let’s begin!
一、选择题
1、在一次函数y=kx+3中,当x=3时,y=6,则k的值为( )
A、-1 B、1
C、5 D、-5
2、已知y是x的正比例函数,如果当x=4时,y=2,那么x=3时,y=( )
A、 B、2 C、3 D、6
一、选择题
2、直线y=kx+b在坐标系中的位
置如图,则( )
-1
-2
x
y
0
(A) k=-2, b=-1
(B) k=-0.5, b=-1
(C) k=-1, b=-2
(D) k=-1, b=-0.5
3、如图,直线是一次函数y=kx+b的图象,那么( )
(A) k>0,b>0;
(B) k>0,b<0;
(C) k<0,b<0;
(D) k<0,b>0。
x
y
0
4、下列说法中不正确的是( )
A、在函数y=2x+1中,y是x的正比例函数;
B、在 中, y是x的正比例函数;
C、在 xy=3 中,y与 成正比例;
D、在圆面积公式S=πR2中,S与R2成正比例
5、从关系式 中,取不同的b值可以得到不同的直线,那么这些直线( )
(A)交于一点; (B)互相平行;
(C)有无数个交点;(D)没有确定的关系。
x
y
6、已知y是x的正比例函数,若y随x增大而减小,且经过点A(3,-a),B(a,-1)两点,那么函数的解析式是( )
(A) ; (B)
(C) ; (D)
7、已知正比例函数y=(3k—1)x,若 y 随x的增大而增大,则k的取值范围是( )
A k<0 B k> 0
C k < D k>
D
3k-1>0
8、若一次函数y=kx-b 满足kb>0且函数值随着x的值的减小而增大,则它的大致图象是( )
y
x
0
y
x
0
y
x
0
y
x
0
(A)
(B)
(C)
(D)
1、若一次函数y=mx-(4m-3)的
图象过原点,则 m= ,若经过
点(0,5),则m= 。
(共6道题)
2、已知y=kx+b的图象上的点
在一、三、四象限内,
则k 0,b 0。
x
y
0
>
<
3、若一次函数的图象经过点A (3,1)
且过点(0,-3),则它的函数关系式
为y= 。
4、已知函数
k为 时,函数是正比例函数,其图象过 象限。函数值y随x的增大而 。
二、四
减小
5、把直线 y=3x 沿 轴
向 .平移2个单位,就得到直线y=3x+2。
x
y
0
y=3x
y=3x+2
2
●
上
6、若一次函数y1=kx+b的图象经过一、二、四象限,则一次函数y2=bx+k的图象经过 象限。
x
y
0
y1=kx+b
y2=bx+k
k<0
b>0
k<0
b>0
一、三、四
(7道题)
1、一次函数y=k1x-4与正比例函数
y=k2x 的图象都经过(2,-1)
①分别求出两个函数的解析式;
②求这两个函数的图象与x轴围成的三角形的面积。
解:①把x=2,y=-1代入两个函数中
-1=2k1-4
-1=2k2
答:两个函数分别是
1、一次函数y=k1x-4与正比例函数
y=k2x 的图象都经过(2,-1)
②求这两个函数的图象与x轴围成的三角形的面积。
解:②画出两个函数图象的草图
0
A
B
x
y
先求直线 与x轴的交点A
1、一次函数y=k1x-4与正比例函数
y=k2x 的图象都经过(2,-1)
②求这两个函数的图象与x轴围成的三角形的面积。
解:②如图画出两个函数的图象
0
A
B
x
y
再求两直线的交点B的坐标
C
└
2、已知函数y=-5xa+b+a-b是正比例函数,求 a-2b 的 值 .
解:由题意可得
a-b=0
∴ a =b
同时有 a+b=1
b+b=1
2b=1
3、如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在的直线为坐标轴建立直角坐标系,使D、A分别在 x 轴、y轴的正半轴上。
(1)求直线AC的解析式;
(2)若EC⊥AC于C,交x 轴于点E,连结AE。
x
y
A
B
C
D
E
0
1
2
┍
F
求证:∠1=∠2
3、如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在的直线为坐标轴建立直角坐标系,使D、A分别在 x 轴、y轴的正半轴上。
(1)求直线AC的解析式;
x
y
A
B
C
D
E
0
1
2
┍
F
解:设直线AC的解析式为:
y=kx+b
将A(0,2),C(2,1)
3、如图,四边形AODB是边长为2的正方形,C为BD中点,以O为原点,OA、OD所在的直线为坐标轴建立直角坐标系,使D、A分别在 x 轴、y轴的正半轴上。
(2)若EC⊥AC于C,交x 轴于点E,
x
y
A
B
C
D
E
0
1
2
┍
F
连结AE。求证:∠1=∠2
4、小芳的存折上已经有500元存款了,从现在开始她每个月可以得到150元的零用钱,小芳计划每月将零用钱的60%存入银行,用以购买她期盼已久的CD随身听(价值1680元)
(1)列出小芳的银行存款(不计利息)
y(元)与月数x 的函数关系式;
(2)多长时间以后,小芳的银行存款才能买随身听?
Y=500+150×60%·x
1680=500+150×60%·x
x≈13.1
答:14个月,小芳的银行存款才能买随身听。
5、已知一次函数y=(p+3)x+(2-q)
(1)p为什么实数时,y随x的增大而增大;
(2)q为什么实数时,函数的图象与y轴的交点在x轴上方;
(3)p、q为什么实数时,函数的图象过原点。
p+3>0
∴ p>- 3
p+3≠0且2-q>0
p+3≠0且2-q=0
6、某自行车保管站在某个星期日接受保管的自行车共有3500辆次,其中变速车保管费是每辆一次0.5元,一般车保管费是每辆一次0.3元。
(1)若设一般车停放的辆次为x,总的保管费收入为y(元),试写出y关于x的函数关系式。
(2)若估计停放的3500辆次自行车中,变速车的辆次不小于25%,不大于40%,试求该保管站这个星期日收入保管费总数的范围。
y=- 0.2x+1750
1225≤x≤1330
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
