北京版三年级数学下册知识提升爬坡题(含解析)
文档属性
| 名称 | 北京版三年级数学下册知识提升爬坡题(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-12 15:22:32 | ||
图片预览




文档简介
第一单元 年、月、日
【例1】2017年5月14日是“母亲节”,请你算一算,2017年的“父亲节”是哪一天?
解析:
“母亲节”是每年五月份的第二个星期日,也就是说,5月14日是星期日。5月是大月,有31天,我们可以先计算出5月31日是星期几:31-14=17(天)17÷7=2(周)……3(天),5月31日就是星期日后面第三天,也就是星期三。
则6月1日是星期四,7-4=3,6月1日加上3天是6月4日,这是6月第一个星期日,“父亲节”是6月份的第三个星期日,6月4日再加上两周,4+14=18,可以推算出,“父亲节”是6月18日。21世纪教育网版权所有
解答:
2017年“父亲节”是6月18日。
【例2】下面是一张二月份的日历,请仔细观察图片,完成练习。
(1)上图是( )年二月份的日历。
A. 2014 B.2008 C.2016
(2)李叔叔从这一年的二月一日开始休假,他正好休息了三个月,你知道他的假期有多少天吗? (3)根据上图,你能推算出这一年的“妇女节”是星期几吗?
解析:
(1)二月是一个特殊的月份,平年二月有28天,闰年二月有29天。从日历上我们看到,这一年的二月只有28天,我们要判断这是哪一年的日历,就要判断所给的三个年份哪一年是平年。如何判断某年是平年还是闰年呢?要看这一年是否是4的倍数,如果是4的倍数就是闰年,如果不是4的倍数就是平年。而遇到整百整千的数字,则必须是400的倍数才是闰年。 21教育网
2014÷4=503……2 2014不是4的倍数,是平年
2008÷4=502 2008是4的倍数,是闰年
2016÷4=504 2016是4的倍数,是闰年
从上面的分析得出2014年是平年,所以这应该是2014年的二月份日历。
(2)李叔叔从二月一日开始休假,假期正好是三个月,应该是2月、3月和4月,2月有28天,3月是大月,有31天,4月是小月,有30天。我们把这3个月的天数加在一起,就是李叔叔假期的总天数:21cnjy.com
28+31+30=89(天)
(3)“妇女节”是3月8日,从日历我们看到2月28日是星期一,那么3月1日就是星期二,8-1=7(天)7÷7=1,从3月1日到3月8日正好过了一周,那么3月8日也是星期二。21·cn·jy·com
解答:
(1)A
(2)28+31+30=89(天)
星期二
【例3】由于帕米尔高原自然环境恶劣,路途艰险难行,守卫祖国边疆的战士们与家里人的书信联系非常困难,邮车也要15天才能来一次,如果邮车在2015年2月1日来到了边防站,那么2016年邮车第一次到达边防站是哪一天(大雪封山等特殊情况忽略不计)?2·1·c·n·j·y
解析:
因为2015÷4=503……3,所以2015年是平年,这一年的2月有28天。我们可以把2月至12月的天数加起来,从而计算出从2015年2月1日到2015年年底有多少天。按平均每个月30天算,再加上6个大月少加的6天,减去2月份多加的2天,减去2月1日这一天,30×11+6-2-1=333(天)。
邮车15天来一次,333÷15=22(次)……3(天),我们可以得出结论,邮车在2015年最后一次来边防站之后还余3天,15-3=12(天),过了2015年底,再有12天,邮车就会到达边防站,所以,2016年邮车第一次到边防站是1月12日。【来源:21·世纪·教育·网】
解答:
2016年1月12日。
【例4】
解析:
要判断这条路能否在国庆节之前修完,需要先算出修这条路需要几天,然后再与9月26日到国庆节的天数相比较。9月是小月,所以只有30天,从9月26日到9月30日的天数为:30-26=4(天),因为9月26日已经开始在修路了,所以要算上这一天,4+1=5(天)。而修路队每天可以修600米,修2000米需要的天数为:2000÷600=3(天)……200(米) 3+1=4(天)再通过比较可以知道国庆节前可以修完这条路。21·世纪*教育网
解答:
30-26=4(天)
4+1=5(天)
2000÷600=3(天)……200(米)
3+1=4(天)
5﹥4
答:国庆节前可以修完这条路。
第二单元 乘法
【例1】仔细观察下面的算式,你能发现什么规律?你能根据这个规律直接写出下面各题的得数吗?
(1)34×11=374
(2)63×11=693
(3)245×11=2695
(4)72×11=__________
(5)618×11=__________
解析:
通过计算、观察可以发现,一个数与11相乘,所得的结果就是将这个数的首位与末位拉开分别作为积的最高位和最低位,再依次将这个数相邻两位由个位加起,和写在十位、百位……www-2-1-cnjy-com
(1)把4写在个位上,3与4的和是7写在十位上,3写在百位,得出34×11=374。
(2)把3写在个位上,6与3的和是9写在十位上,6写在百位,得出63×11=693。
(3)把5写在个位上,4与5的和是9写在十位上,2与4的和是6写在百位上,2写在千位,得出245×11=2695。www.21-cn-jy.com
(4)72×11也用同样的方法:把2写在个位,7与2的和是9写在十位,7写在百位,得出72×11=7922-1-c-n-j-y
(5)618×11,把8写在个位,1与8的和是9写在十位,6与1的和是7写在百位,6写在千位,得出618×11=679821*cnjy*com
解答:
(4)72×11=792
(5)618×11=6798
【例2】下面竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。请求出这些汉字所代表的数字。【来源:21cnj*y.co*m】
甲( ) 乙( )
丙( ) 丁( )
解析:
4的乘法口诀的末尾数字可能为:0,2,4,6,8, 甲位于整个算式乘积的末位,所以甲有可能是0,2,4,6,8,甲乘4没有满十进位,又因为甲在第一个因数的首位不可能是0,所以甲只能是2。则丁与4的乘积末位数为2,3×4=12或8×4=32,那么丁有可能是3或者8,丁是整个算式乘积的第一位数,甲×4=2×4=8,所以丁不可能是3,只能是8。因为丁是8,证明乙乘4没有向前一位进位,那么乙乘4的积不满十,乙有可能是1或者2,甲是2,乙只能是1。丙就是7,
丙×4=7×4=28,加上后面进上来的3正好是31,向前一位进3,乙×4=1×4=4,4+3=7。因数=甲乙丙丁=2178,积=丁丙乙甲=8712【出处:21教育名师】
解答:
【例3】超市新运来25箱苹果,每箱应该是30千克,可是其中一箱在运输途中破损丢失了12千克,你知道超市这一批一共运来多少千克苹果吗?
解析:
方法一:每箱苹果有30千克,我们可以先求出25箱苹果一共多少千克,然后再减去丢失的12千克。
方法二:25箱苹果,有一箱是破损的,少了12千克,还剩30-12=18(千克),其余的24箱,每箱是30千克,一共有30×24=720(千克),再加上18千克,就是这批苹果的总重量。【版权所有:21教育】
解答:
方法一: 30×25-12 方法二:30-12=18(千克)
= 750-12 30×24+18
= 738(千克) = 720+18
= 738(千克)
答:这批苹果一共有738千克。
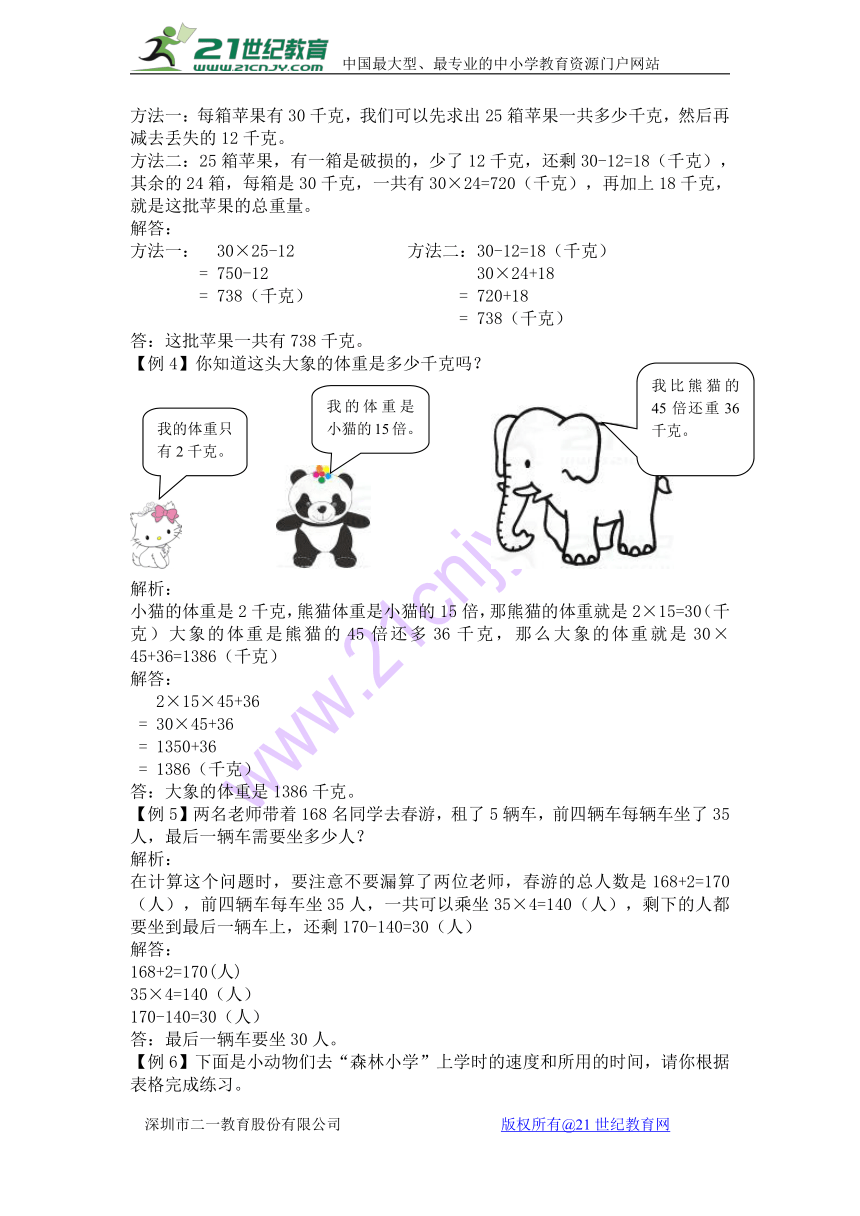
【例4】你知道这头大象的体重是多少千克吗?
解析:
小猫的体重是2千克,熊猫体重是小猫的15倍,那熊猫的体重就是2×15=30(千克)大象的体重是熊猫的45倍还多36千克,那么大象的体重就是30×45+36=1386(千克)21教育名师原创作品
解答:
2×15×45+36
= 30×45+36
= 1350+36
= 1386(千克)
答:大象的体重是1386千克。
【例5】两名老师带着168名同学去春游,租了5辆车,前四辆车每辆车坐了35人,最后一辆车需要坐多少人?21*cnjy*com
解析:
在计算这个问题时,要注意不要漏算了两位老师,春游的总人数是168+2=170(人),前四辆车每车坐35人,一共可以乘坐35×4=140(人),剩下的人都要坐到最后一辆车上,还剩170-140=30(人)
解答:
168+2=170(人)
35×4=140(人)
170-140=30(人)
答:最后一辆车要坐30人。
【例6】下面是小动物们去“森林小学”上学时的速度和所用的时间,请你根据表格完成练习。
动物
速度(米/分)
82
69
78
93
时间(分钟)
18
51
32
42
(1)估算一下,每个小动物家到学校大约多少米?
(2)哪个小动物距离学校最远?
解析:
(1)小熊每分钟走82米,从家到学校需要18分钟,那它家到学校的距离应该用算式82×18来计算,根据四舍五入的原则82≈80,18≈20,82×18≈1600(米)
小兔子每分钟走69米,大约是70米,走了51分钟,估算时按50去计算,那么小兔子家到学校的距离为69×51≈3500(米)
小老虎每分钟走78米,大约为80米,走了32分钟,四舍五入为30分钟,那么我们估算小老虎从家到学校用78×32≈2400(米)
小马每分钟走93米,大约为90米,走了42分钟,估算时按40分钟计算,那么小马从家到学校的距离为93×42≈3600(米)
(2)在上一小题中我们已经计算出了每个小动物家与学校的距离,我们通过比较可以得出:3600﹥3500﹥2400﹥1600,可以知道小马家离学校最远。
解答:
(1)82×18≈1600(米)
69×51≈3500(米)
78×32≈2400(米)
93×42≈3600(米)
答:小熊家距离学校大约1600米,小兔子家距离学校大约3500米,小老虎家距离学校大约2400米,小马家距离学校大约3600米。
(2)3600﹥3500﹥2400﹥1600
答:小马家离学校最远。
第三单元 吨的认识
【例1】这几辆卡车能同时通过这座大桥吗?
解析:要判断这三辆卡车能不能同时通过这座大桥,我们需要将三辆卡车的总重量计算出来,第一辆车重量为2吨500千克,第二辆车重1吨350千克,第三辆车重1吨700千克,三辆车共重:2吨500千克+1吨350千克+1吨700千克=5吨550千克,所以,这三辆车不能同时通过这座大桥。
解答:
2吨500千克+1吨350千克+1吨700千克=5吨550千克,
答:这三辆车不能同时通过这座大桥。
【例2】森林里有一头野猪,一头大象,一头犀牛,一共重12吨。已知一头野猪和一头犀牛共重7吨;一犀牛和一头大象共重9吨,问:野猪、大象和犀牛各重多少吨?
解析:
因为根据一头野猪和一头犀牛共重7吨,即野猪+犀牛=7吨,一头犀牛和一头大象共重9吨,即大象+犀牛=9吨,所以就可以知道:野猪+2只犀牛+大象的重量是7+9=16(吨),再根据一头野猪,一头大象,一头犀牛,一共重12吨(野猪+犀牛+大象=12吨),就可以知道一头犀牛重 16—12=4(吨);犀牛和野猪共重7吨,那么野猪的重量是7—4=3(吨);同理,根据大象+犀牛=9吨,可以求出大象的重量为9-4=5(吨)。
解答:
7+9=16(吨)
16-12=4(吨)
7-4=3(吨)
9-4=5(吨)
答:野猪重3吨,犀牛重4吨,大象重5吨。
【例3】果园收获了18箱苹果和25箱梨,每箱苹果50千克,每箱梨42千克,这些水果用一辆载重1吨的汽车两次能运完吗?
解析:
我们首先应该求出水果的总重量,根据题意,苹果是18箱,每箱50千克,则苹果的重量为50×18=900(千克),梨有25箱,每箱42千克,则梨的重量为42×25=1050(千克),苹果和梨共重900+1050=1950(千克)
载重1吨的汽车两次可以运2吨,2吨=2000千克,2000﹥1950,所以用一辆载重1吨的汽车两次可以运完。
解答:
50×18=900(千克)
42×25=1050(千克)
2吨=2000千克
2000﹥1950
答:用一辆载重1吨的汽车两次可以运完。
【例4】发电厂需要运16吨煤,大货车限载6吨,小货车限载4吨,如果每次每辆车都装满,怎样安排能恰好运完16吨煤呢?
限载6吨 限载4吨
解析:我们可以通过下面的表格列出几种安排车辆的方案:
方案
大货车(辆)
小货车(辆)
载重总量(吨)
方案一
0
4
16
方案二
1
3
18
方案三
2
1
16
方案四
3
0
18
通过上面的表格,我们可以看出,方案一和方案四在每辆车每次都装满的情况下,正好可以运完16吨。
解答:
有两种方案:
(一)安排4辆小货车。4×4=16(吨)
(二)安排2辆大货车,1辆小货车。2×6+4=16(吨)
第四单元 解决问题
【例1】李伯伯家养了7头奶牛,平均每头奶牛每天产20千克牛奶,这些奶牛9月份一共能产多少千克牛奶?
解析:
我们可以先求出7头奶牛每天产奶多少千克,根据提议,平均每头奶牛每天产奶28千克,7头奶牛可以产奶:20×7=140(千克),9月份是小月,只有30天,要求9月份一共能产多少千克牛奶,就是求这些奶牛30天可以产奶多少千克140×30=4200(千克)
解答:
20×7×30
= 140×30
= 4200(千克)
答:这些奶牛9月份一共能产4200千克奶。
【例2】学校操场有一段跑道长80米,东东每天在这段跑道上跑4个来回,他每天跑多少米?
解析:
解答本题的关键在于理解1个来回是分来和回两个80米,4个来回就是在跑道上跑4个2次,4×2=8(次),跑道长80米,则4个来回是80×8=640(米)
解答:
80×4×2
= 320×2
= 640(米)
答:东东每天跑640米。
【例3】
解析:
两只青蛙每天可以吃掉28只害虫,根据这个条件,我们可以计算出每只青蛙每天吃多少只害虫:58÷2=29(只),然后可以求出4只青蛙每天吃掉多少只害虫:29×4=116(只),一星期是7天,116×7=812(只)
解答:
58÷2=29(只)
29×4×7
= 116×7
= 812(只)
答:4只青蛙一星期可以吃掉812只害虫。
【例4】小猴子小松鼠和小熊猫分苹果。
你知道原来一共有多少个苹果吗?
解析:
小松鼠分得剩下的一半多一个,小熊猫得到6个,也就是剩下的一半少一个,那么6+1=7(个),剩下的一半也就是7个,我们可以求出分给小猴子后剩下的有多少个:7×2=14(个)。小猴子分得总数的一半多一个,那么剩下的14个也就是总数的一半少一个,我们可以求出总数的一半为14+1=15(个),然后可以用15×2=30(个)计算出原来一共有30个苹果。
解答:
6+1=7(个)7×2=14(个)14+1=15(个)15×2=30(个)
答:原来一共有30个苹果。
【例5】小松鼠采来一些松果,它把这些松果分成3份,其中两份送给了妈妈,自己留下的一份又分成了4份,3份给了自己的弟弟妹妹们,自己只剩下9个,你知道小松鼠一共采来多少个松果吗?
解析:
小松鼠最后自己剩下的一份是9个松果,那么我们可以求出它送给妈妈后自己留下的一份分成的4份一共有多少个松果:9×4=36(个),这是小松鼠把采来的松果分成3份后,其中的一份又36个,我们可以求出3份有多少个:36×3=108(个)
解答:
9×4×3
= 36×3
= 108(个)
答:小松鼠一共采来108个松果。
【例6】打一份630字的文件,王阿姨原来要用9分钟,现在只需6分钟,王阿姨现在每分钟比原来多打多少个字?
解析:
要求王阿姨现在每分钟比原来多打多少个字,我们要求出王阿姨原来每分钟打多少个字,现在每分钟打多少个字。原来打630字需要9分钟,每分钟打的字数为:630÷9=70(个),现在打630字只需要6分钟,每分钟打的字数为:630÷6=105(个)然后用现在每分钟打字的数减去原来每分钟打的字数,105-70=35(个)
解答:
630÷9=70(个)
630÷6=105(个)
105-70=35(个)
答:王阿姨现在每分钟比原来多打35个字。
【例7】学校举行体操比赛,把参赛的选手平均分成4个组,每组淘汰了24人后,剩下的总人数正好相当于原来的一组,一共有多少人参加了体操比赛?
解析:
参加体操比赛的人平均分成了四个组,每组淘汰了24人,4个组一共淘汰了24×4=96(人),剩下的人数正好和原来一组的人数相等,4-1=3(组),那么淘汰的人数就和原来3组的人数相等,96÷3=32(人),可以求出每组有32人,根据题意,可以求出4个组的人数为:32×4=128(人)
解答:
24×4=96(人)
4-1=3(组)
96÷3=32(人)
32×4=128(人)
答:一共有128人参加了体操比赛。
第五单元 长方形和正方形的面积
【例1】用4个边长是2厘米的正方形卡片拼图形,如果拼成一个长方形,长方形的长是( )厘米,宽是( )厘米,它的面积是( )平方厘米;如果拼成一个正方形,拼成的正方形的边长是( )厘米,它的面积是( )平方厘米。
解析:
4个边长是2厘米的正方形卡片拼成长方形,如下图:
从图中可以看出拼成的长方形长是原来正方形的4倍,2×4=8(厘米),宽就是正方形的边长2厘米,长方形的面积=长×宽,2×8=16(平方厘米)。
4个边长是2厘米的正方形卡片拼成正方形,如下图:
从图中可以看出,拼成的正方形的边长是原来小正方形边长的2倍,2×2=4(厘米),正方形的面积=边长×边长,4×4=16(平方厘米)
解答:
用4个边长是2厘米的正方形卡片拼图形,如果拼成一个长方形,长方形的长是( 8 )厘米,宽是( 2 )厘米,它的面积是( 16 )平方厘米;如果拼成一个正方形,拼成的正方形的边长是( 4 )厘米,它的面积是( 16 )平方厘米。
【例2】下面的长方形的面积是多少?(每个小方格表示1平方厘米)
解析:
从图中可以看出,这个长方形的长为5厘米,宽为3厘米,长方形的面积为5×3=15(平方厘米)
【例3】一个边长为10米的正方形花坛,如果这个花坛的的边长扩建到原来的2倍,那么这个花坛的面积比原来增加了多少?
解析:
要知道扩建后的花坛面积比原来增加了多少,需要分别求出花坛扩建前后的面积,这是花坛扩建前后都是正方形,要求正方形的面积,需要知道正方形的边长,正方形的面积=边长×边长,根据题意,这个花坛扩建前的边长为10米,那么扩建前正方形花坛的面积为:10×10=100(平方米)。经过扩建,这个花坛的边长扩大到原来的2倍,10×2=20(米)那么扩建后的面积为:20×20=400(平方米),这个花坛的面积比原来增加了400-100=300(平方米)
解答:
10×10=100(平方米)
10×2=20(米)
20×20=400(平方米)
400-100=300(平方米)
答:这个花坛的面积比原来增加了300平方米。
【例4】如下图,小正方形的边长为3厘米,大正方形的面积是小正方形面积的4倍,大正方形的周长比小正方形的周长多多少厘米?
解析:
我们要比较大正方形的周长比小正方形的周长多多少,要先分别求出两个正方形的周长,小正方形的边长在题目中已经告诉我们是3厘米,我们可以直接求出小正方形的周长为3×4=12(厘米),根据题意,大正方形的面积是小正方形面积的4倍,小正方形的面积=3×3=9(平方厘米),大正方形的面积=9×4=36(平方厘米),因为36=6×6,我们可以判断出大正方形的边长为6厘米,那么大正方形的周长为:6×4=24(厘米),然后用大正方形的周长减去小正方形的周长:24-12=12(厘米)
解答:
3×4=12(厘米)
3×3=9(平方厘米)
9×4=36(平方厘米)
36=6×6 大正方形的边长为6厘米。
6×4=24(厘米)
24-12=12(厘米)
答:大正方形的周长比小正方形的周长多12厘米。
【例5】一个长方形的周长是50分米,如果长方形的长是20分米,那么这个长方形的面积是多少平方米?
解析:
长方形的周长=(长+宽)×2,那么,长方形的宽=周长÷2-长,根据这个公式,我们可以求出长方形的宽为:50÷2-20=5(分米),这个长方形的面积为:长方形的面积=长×宽=20×5=100(平方分米),我们知道平方米和平方分米之间的进率为100,100平方分米=1平方米。
解答:
50÷2-20=5(分米)
20×5=100(平方分米)
100平方分米=1平方米
答:这个长方形的面积为1平方米。
【例6】学校有一个长15米,宽8米的长方形花坛,准备在花坛四周修建一条1米宽的小路,小路的面积是多少平方米?
解析:
沿着花坛四周修建了一条小路后,小路的外侧边沿又形成了一个大的长方形,小路的面积等于大长方形的面积减去长方形花坛的面积,花坛的面积为:长方形面积=长×宽=15×8=120(平方米);大长方形的长等于花坛的长加上小路宽度的两倍,也就是15+1+1=17(米),大长方形的宽等于花坛的宽加上小路宽度的两倍,也就是8+1+1=10(米)。大长方形的面积为:17×10=170(平方米)。然后用大长方形的面积减去长方形花坛的面积,就是小路的面积:170-120=50(平方米)
解答:
15×8=120(平方米)
15+1+1=17(米)
8+1+1=10(米)
17×10=170(平方米)
170-120=50(平方米)
答:小路的面积为50平方米。
第六单元 分数的初步认识
【例1】两条同样长的绳子,第一条剪去了,第二条剪去了,哪一条剪去的长一些?
解析:
两条绳子同样长,第一条剪去了,第二条剪去了,我们可以通过比较这两个分数的大小来判断哪一条绳子剪去的长一些,和分子相同,分母不同,比较分子相同的分数大小,分母越小,分数越大,所以>,第一条绳子剪去的更长一些。
解答:
>,第一条绳子剪去的更长一些。
【例2】小兔子和小猴子摘了一个大西瓜,平均切成了九块。
这个西瓜吃完了吗?
解析:
(一)小猴子吃了西瓜的,小兔子吃了西瓜的,我们可以求出它们一共吃了这个西瓜的几分之几,+=,当分子分母相同时这个分数等于1,所以,这个西瓜吃完了。
(二)我们还可以这样想,这个西瓜平均切成了9块,小猴子吃掉了这个西瓜的,也就是吃掉了6块,小兔子吃掉了这个西瓜的,也就是吃掉了3块,它们一共吃掉了6+3=9(块),这个西瓜正好吃完。
解答:
+==1
答:这个西瓜吃完了。
【例3】写出下面阴影部分表示的分数。
(1) (2)
( ) ( )
解析:
(1)这个图形的整体也就是“单位1”是大正方形,我们可以看做把大正方形平均分成9个小正方形,阴影部分由一个小正方形和两个三角形组成,两个小三角形可以拼成一个小正方形,如图:
那么,阴影部分也就是两个小正方形,也就是大正方形的。
(2)整个图形由两个圆组成,阴影部分又分为两块,大的半圆相当于把大圆平均分成2份,占其中的一份,小的半圆相当于把小圆平均分成2份,占其中的一份,那么阴影部分就等于把这两个圆平均分成2份,占其中的一份,也就是。
解答:
(1) (2)
【例4】妈妈买了两块同样的蛋糕,把其中的一块平均分成6小块,爸爸吃了1小块,妈妈也吃了1小块。把另一块平均分成3小块,小雨吃了其中的1小块。哪一块剩下的多?
解析:
根据题意,妈妈把其中一块蛋糕平均分成8小块,爸爸吃了1块,妈妈也吃了1块,那么还剩8-1-1=6(块),剩下的4块占这块蛋糕的,另一块同样大小的蛋糕被分成了4块,小雨吃了其中的1块,剩下3块,剩下的占整个蛋糕的,如下图:
我们可以从图中看出,=,所以,这两块蛋糕剩下的部分同样多。
解答:
这两块蛋糕剩下的部分同样多。
第七单元 小数的初步认识
【例1】爸爸买了一瓶色拉油,连瓶共重3.4千克,用去一半油后连瓶重1.9千克,你知道这瓶油原来有多少千克?瓶有多重?
解析:
这瓶色拉油刚买来时,连瓶重3.4千克,用去一半后连瓶重1.9千克,用去了3.4-1.9=1.5(千克),也就是说,这瓶色拉油的一半是1.5千克,那这瓶色拉油的重量为:1.5+1.5=3(千克),瓶+色拉油=3.4,那么瓶子的重量为:3.4-3=0.4(千克)
解答:
3.4-1.9=1.5(千克)
1.5+1.5=3(千克)
3.4-3=0.4(千克)
答:这瓶油原来重3千克,瓶子重0.4千克。
【例2】用数字6,2,8和小数点可以组成哪些没有重复数字的一位小数(每个数字都用上)?这些小数中最大的是多少?最小的是多少?
解析:
这里有3个数字,分别是6,0,8,用这几个数字组成一位小数, 小数部分为6的数字有:82.6, 28.6;小数部分是8的数字为:62.8, 26.8;小数部分为2的数字有:68.2, 86.2。比较小数的大小,我们应该先比较整数部分,整数部分大的数就大;如果整数部分相同,在比较小数部分,小数部分大的数字就大。我们刚组成的数字整数部分都不同,最大的是86.2,最小的是26.8。
解答:
用数字6,2,8和小数点可以组成哪些没有重复数字的一位小数有:82.6, 28.6, 62.8, 26.8, 68.2, 86.2。
最大的是86.2,最小的是26.8。
【例3】下面是田径运动会中4名运动员在50米赛跑中的成绩,你能帮他们按从快到慢的顺序排一排名次吗?
姓名
小红
小明
小丽
小军
成绩/秒
8.9
7.9
8.2
7.8
解析:
本题中要给这些运动员按从快倒慢的顺序排名次,要比较他们的成绩,成绩是用时间来计算的,谁用的时间最短谁跑的最快。在比较这些小数的大小时,我们先比较整数部分,整数部分大的数就大,其中小红和小丽的成绩分别为8.9和8.2,小明和小军的成绩为7.9和7.8,整数部分为8的数字大,再分别比较8.9和8.2的小数部分,2<9,所以8.2<8.9。而7.9和7.8的小数部分,8<9,所以7.8<7.9,我们按从小到大的顺序排列这些数字:7.8<7.9<8.2<8.9,然后我们可以根据这个顺序排出赛跑的名次:第一名:小军;第二名:小明;第三名:小丽;第四名:小红。
解答:
7.8<7.9<8.2<8.9
第一名:小军;第二名:小明;第三名:小丽;第四名:小红。
【例4】写出符合下列要求的小数。
(1)使这个数最大,这个数是( )。
(2)使这个数最接近81,这个数是( )。
(3)使这个数最小,这个数是( )。
解析:
(1)要使这个数最大,两个方框里都应该填最大的一位数,也就是9,那么这个数字就是90.9。
(2)最接近81的一位小数有两个,一个是80.9,一个是81.1,现在这个小数的个位是0,也就只能是80.9。
(3)要使这个数最小,这两个方框里都应该写最小的一位数,0不能写在首位,那么这个数为10.0
解答:
(1)90.9 (2)80.9 (3)10.0
【例5】一支铅笔0.6元,比一个文具盒便宜8.5元,小明买一支铅笔和一个文具盒,10元够吗?
解析:
首先我们可以求出一个文具盒多少元,根据题意,一支铅笔0.6元,比一个文具盒便宜8.5元,也就是说,一个文具盒比一支铅笔多用8.5元钱,一个文具盒的价格为:0.6+8.5=9.1(元)。然后求出一支铅笔盒一个文具盒一共用多少钱,9.1+0.6=9.7(元),10>9.7,所以小明带了10元够了。
解答:
0.6+8.5=9.1(元)
9.1+0.6=9.7(元)
10>9.7
答:10元钱够了。
【例5】下面是妈妈到超市购物的一张票据。
欢迎光临红星超市
流水号:000120456
收款台:001 收银员:0150
商品名称 数量 单价 总额
可乐 1 2.5 2.5
饼干 1 6.9 6.9
应收金额:
现金:
交易找零:0.6
(1)应收金额是多少?
(2)妈妈付给收银员多少钱?
解析:
(1)应收金额是妈妈购买的所有商品的价格之和,妈妈买了两件商品,一瓶可乐,用去2.5元,一盒饼干用去6.9元,一共用了2.5+6.9=9.4(元),应该付9.4元。
(2)根据上面计算的结果,妈妈应付9.4元,从图表中可以看到,找零0.6元,应付金额加上找零就是妈妈付给收银员的金额,9.4+0.6=10(元)
解答:
(1)2.5+6.9=9.4(元)
答:应付金额是9.4元。
(2)9.4+0.6=10(元)
答:妈妈付给收银员10元。
【例6】买玩具。
5.4元 18.2元 9.9元 15元
(1)买一根跳绳和一个玩具熊一共多少钱?
(2)玩具汽车比玩具熊贵多少钱?
(3)小丽有30元钱,想买两件玩具,可以怎么买?
解析:
(1)一根跳绳5.4元,一个玩具熊9.9元,根据题意可以求出这两种玩具一共用多少钱:5.4+9.9=15.3(元)。
(2)一辆玩具汽车18.2元,一个玩具熊9.9元,求玩具汽车比玩具熊贵多少元,可以用玩具汽车的价格减去玩具熊的价格:18.2-9.9=8.3(元)。
(3)小丽有30元,想买两件玩具,那么她买的两件玩具的价格总和不能超过30元,这里价钱比较贵的两件玩具是小汽车和篮球,这两种玩具的价格总和为:18.2+15=33.2(元),已经超过了30元,所以不能买这两种玩具,其他两种玩具都不超过10元,所以可以随意搭配,比如:买一根跳绳和一个篮球;买一辆玩具小汽车和一个玩具熊;买一个篮球和一个玩具熊等等。
解答:
(1)5.4+9.9=15.3(元)。
答:买一根跳绳和一个玩具熊一共15.3元。
(2)18.2-9.9=8.3(元)
答:玩具汽车比玩具熊贵8.3元。
(3)买一根跳绳和一个篮球:5.4+15=20.4(元)(答案不唯一)
答:可以买一根跳绳和一个篮球,用去20.4元。
第八单元 认识方向
【例1】小明想给来学校参观的客人画一个简单的平面图,你能帮帮他吗?
解析:
我们在画平面示意图时,通常按照“上北下南,左西右东”的原则,根据这个原则,以教学楼为观测点,确定“东西南北”四个方向,然后根据题目的叙述就可以绘制出平面图。
解答:
【例2】蜗牛和蚂蚁要去甲壳虫家。
(1)蜗牛先向( )走( )米,再向( )走( )米,就到达甲壳虫家。
(2)蚂蚁先向( )走( )米,再向( )走( )米,就到达甲壳虫家。
解析:
(1)小蜗牛有两条路线,第一条:它要先向西走一个格,也就是2米,再向北走三个格,也就是6米。第二条:它先向北走三个格,也就是6米,然后再向西走一个格,也就是2米。
(2)给小蚂蚁画的路线中,也有两条,第一条:蚂蚁先向东走2格,也就是4米,再向北走2格,也就是4米,就可以到达甲壳虫家。第二条:它要先向西走1格,也就是2米,再向北走1格,也就是2米,再向东走1格,也是2米,再向北走1格,也就是2米,再向东走2格,也就是4米到达甲壳虫家。
解答:
(1)西,2,北,6(答案不唯一)
(2)东,4,北,4
【例3】帮助小动物找家.
(1)森林公园的东北角住着小花猫. (2)小羊住在森林公园的东面.
(3)小羊的南面住着小兔. (4)小花猫的西面住着小鹿.
(5)森林公园的西南角住着小牛. (6)小牛的东面住着小猪.
(7)熊猫住在小牛的北面. (8)狐狸住在熊猫的北面.
解析:
我们首先以“森林公园”为观测点,小羊住在森林公园的东面(右东),确定小花猫在森林公园的东北方向(示意图右上角),小牛住在森林公园的西南角(示意图左下角);然后再以小羊家为观测点,确定小兔的位置是在小羊的南面(小羊下面)。以小花猫家为观测点,小鹿在小花猫西面(小花猫左面)。再以小牛家为观测点,小牛家的东面住着小猪(小牛右面),熊猫家在小牛家的北面(小牛的上面)。以熊猫家为观测点,确定狐狸家住在熊猫家的北面(熊猫上面)
解答:
【例4】在括号里填上正确的方向。
(1)男孩前面是( ),左面是( ),右面是( )。
(2)如果男孩转向他的左手方向,那他前面是( ),后面是( )。
解析:
(1)这个男孩的背面是西,前面是和西相反的方向,就是东方,左面是北,右面是南。
(2)如果男孩转向的他的左手方向,他的左边是北,那么现在他面对着北方,后面就是南方。
解答:
(1)东, 北, 南
(2)北, 南
【例5】小晴从家出发向北走100米到学校,小晴家在哪里?图中( )表示小晴家。(填字母)
解析:
根据题意,小晴从家出发向北走100米到达学校,我们来观察A、B、C三个点,A点到学校需要向西走100米,所以A点不是小晴的家,C点到学校需要先向北走100米,然后再向西走100米,所以C点不是小晴的家,只有在B点是向北走100米到达学校,所以B点是小晴的家。
解答:
图中(B)表示小晴家。
第九单元 整理数据
【例1】下面是三年级一班同学们9月份作业得星情况记录单,请你帮老师整理一下这些数据吧。
(1)整理记录单中的数据,把得到的结果填入统计表中,并根据统计表回答问题。
得星等级
A(60~80)
B(40~59)
C(20~39)
D(0~19)
人数
(2)得星数在40颗以上的是良好,良好的学生有多少人?
(3)你还能提出什么数学问题?
(4)你认为D等级的同学应该怎样做呢?
解析:
得星等级
A(60~80)
B(40~59)
C(20~39)
D(0~19)
人数
一
(1)这是一份学生作业得星情况的记录单,通过观察记录单我们可以发现,得星最多的是75颗,最少的是14颗,然后统计表将得星情况按每20颗一段进行统计整理。在整理数据时,要按先后顺序逐个统计,每个数据在哪个等级,可以先用画“正”字的方法在那个等级画上一笔,这样可以避免重复或遗漏。统计之后还要数一数统计的总人数是否与记录单的总人数相等。
得星等级
A(60~80)
B(40~59)
C(20~39)
D(0~19)
人数
8
11
8
3
(2)得星数在40颗以上的是良好,那么良好包括两个等级:A等级和B等级,A等级有8人,B等级有11人,那么良好的人数为:8+11=19(人)
(3)根据统计表可以提出很多数学问题,比如:得星数在40颗以下的有多少人?
得星数在40颗以下的包括C等级和D等级,一共有:8+3=11(人)
(4)D等级是得星数最少的同学,可以建议他们认真完成作业,严格要求自己,遇到不明白的问题向老师、同学、家长求教等等。
解答:
(1)
(2)8+11=19(人)
得星等级
A(60~80)
B(40~59)
C(20~39)
D(0~19)
人数
8
11
8
3
答:良好的人数为19人。
(3)得星数在40颗以下的有多少人?
8+3=11(人)
答:得星数在40颗以下的有11人.
(4)我建议D等级的同学,上课认真听讲,课下严格按老师的要求完成作业,遇到不明白的问题主动寻求老师、同学或家长的帮助。
第十单元 数学百花园
【例1】植树节学校组织家长和孩子们去植树,1组有3名家长和5名同学,共植树22棵,2组有5名家长和5名同学共植树30棵树,如果每个家长植树的数目相同,每名同学植树的数目也相同,你能计算出每个家长植树多少棵,每个同学植树多少棵吗?
解析:
我们可以将题中的数量关系转化成文字算式,进行比较:
1组:3名家长植树棵树+5名同学植树棵树=22棵
2组:5名家长植树棵树+5名同学植树棵树=30棵
从上面的文字关系式中,我们可以推算出,相差的8棵树就是2名家长植树的棵数。也就是说2名家长植树8棵。
我们可以求出每名家长植树的棵数:8÷2=4(棵)
然后可以求出1组的三名家长植树棵树为:4×3=12(棵)
1组一共植树22棵,减去家长植的12棵,剩下的就是5名同学植树的棵数:22-12=10(棵)
然后我们就可以求出每名同学植树的棵数:10÷5=2(棵)
解答:
5-3=2(名)
8÷2=4(棵)
4×3=12(棵)
22-12=10(棵)
10÷5=2(棵)
答:每名家长植树4棵,每名学生植树2棵。
【例2】明明、欣欣和乐乐一起去买水果,明明买了8个苹果、6个橘子和3个桃子共用去36元,欣欣买了5个苹果、6个橘子和3个桃子共用去27元,乐乐买了5个苹果和6个橘子用去21元,你知道每种水果的单价是多少吗?
解析:
明明买的水果:
8个苹果+6个橘子+3个桃子=36元
欣欣买的水果:
5个苹果+6个橘子+3个桃子=27元
通过比较我们发现,明明只比欣欣多买了3个苹果,他比欣欣多用了36-27=9元钱,也就是说3个苹果用去9元钱,每个苹果用9÷3=3(元)
乐乐比欣欣少买了3个桃子,少用了27-21=6(元)钱,这6元就是3个桃子的价格,每个桃子价格为:6÷3=2(元)
然后我们计算乐乐买了5个苹果用去的钱数:5×3=15(元)
乐乐一共用了21元,从21元中减去买苹果的15元,就是买6个橘子用去的钱数:21-15=6(元)6÷6=1(元)每个橘子1元钱。
解答:
8-5=3(个)36-27=9(元)9÷3=3(元)
27-21=6(元)6÷3=2(元)
5×3=15(元)21-15=6(元)6÷6=1(元)
答:苹果:3元 橘子:1元 桃子:2元
【例3】粮店运来一批粮食,4袋大米和5袋面粉共重300千克,2袋大米和3袋面粉共重170千克,一袋大米和一袋面粉各重多少千克?
解析:
我们先把题目中的条件转化成文字式进行观察:
4袋大米+5袋面粉=300千克
2袋大米+3袋面粉=170千克
上面的算式中大米的数量和面粉的数量都不相同,但是我们发现,第一个算式中大米的数量是第二个算式中数量的2倍,那么我可以将第二个算式中大米和面粉的数量都乘2:4袋大米+6袋面粉=340千克。
然后再比较两个算式:
4袋大米+5袋面粉=300千克
4袋大米+6袋面粉=340千克
两个算式只相差6-5=1(袋)面粉,相差的重量为:340-300=40(千克),可以算出一袋面粉的重量为40千克。
然后我们再计算3袋面粉的重量:40×3=120(千克)
2袋大米的重量为:170-120=50(千克)
每袋大米重:50÷2=25(千克)
解答:
170×2-300=40(千克)
40×3=120(千克)
170-120=50(千克)
50÷2=25(千克)
答:每袋大米重25千克,每袋面粉重40千克。
【例3】用一个杯子向空瓶里倒水,如果倒进3杯水,连瓶共重440克;如果倒进5杯水,连瓶共得600克。那么,一杯水与一个空瓶共重多少千克?
解析:
3杯水+瓶=440克 (1)
5杯水+瓶=600克 (2)
我们可以比较:为什么(1)(2)两个算式相差了600-440=160克。因为两个算式相差了2杯水,也就是2杯水的重量为160克。
我们可以求出1杯水的重量为:160÷2=80(克)
那么3杯水重量为:80×3=240(克)
空瓶的重量为:440-240=200(克)
解答:
600-440=160(克)
160÷2=80(克)
80×3=240(克)
440-240=200(克)
答:一杯水的重量为80克,一个空瓶的重量为200克。
【例4】星期天,小丽要做完下面表格中的这些事,最少需要多少分钟?
洗碗
收拾客厅
拿衣服去洗
拖地
洗衣机洗衣服
晾衣服
5分钟
12分钟
1分钟
10分钟
30分钟
5分钟
解析:
要想用最少的时间完成这些事情,能同时做的事情尽量同时做,比如在洗衣机洗衣服时小丽可以去洗碗、收拾客厅、拖地,这样就可以节约出一部分时间。小丽可以像下面示意图那样去安排时间:
解答:
1+30+5=36(分钟)
答:小丽最少需要36分钟。
【例5】小梅、小晴、小娟同时来到医务室,小梅看牙需要7分钟,小晴量体温需要5分钟,小娟拿药需要4分钟,怎样合理安排他们的治疗顺序,使她们等候时间总和最少,他们一共要用多少时间?
解析:
要想让等候时间总和最少,要按所用时间从短到长的顺序来安排,也就是先让用时最少的小娟拿药,她需要4分钟,另外两个人需要各等4分钟;然后让小晴量体温,她需要5分钟,小梅需要再等5分钟;最后让小梅看牙,她需要7分钟,她们各自用的时间为:
小娟:4分钟(拿药)
小晴:4分钟(等候)+5分钟(量体温)=9分钟
小梅:4分钟(等候)+5分钟(等候)+7分钟(看牙)=16分钟
那她们用的时间总和为:4+9+16=29(分钟)
解答:
先让小娟拿药,然后小晴量体温,最后小梅看牙。
小娟:4分钟(拿药)
小晴:4分钟(等候)+5分钟(量体温)=9分钟
小梅:4分钟(等候)+5分钟(等候)+7分钟(看牙)=16分钟
那她们用的时间总和为:4+9+16=29(分钟)
答:她们用的时间总和为29分钟。
【例1】2017年5月14日是“母亲节”,请你算一算,2017年的“父亲节”是哪一天?
解析:
“母亲节”是每年五月份的第二个星期日,也就是说,5月14日是星期日。5月是大月,有31天,我们可以先计算出5月31日是星期几:31-14=17(天)17÷7=2(周)……3(天),5月31日就是星期日后面第三天,也就是星期三。
则6月1日是星期四,7-4=3,6月1日加上3天是6月4日,这是6月第一个星期日,“父亲节”是6月份的第三个星期日,6月4日再加上两周,4+14=18,可以推算出,“父亲节”是6月18日。21世纪教育网版权所有
解答:
2017年“父亲节”是6月18日。
【例2】下面是一张二月份的日历,请仔细观察图片,完成练习。
(1)上图是( )年二月份的日历。
A. 2014 B.2008 C.2016
(2)李叔叔从这一年的二月一日开始休假,他正好休息了三个月,你知道他的假期有多少天吗? (3)根据上图,你能推算出这一年的“妇女节”是星期几吗?
解析:
(1)二月是一个特殊的月份,平年二月有28天,闰年二月有29天。从日历上我们看到,这一年的二月只有28天,我们要判断这是哪一年的日历,就要判断所给的三个年份哪一年是平年。如何判断某年是平年还是闰年呢?要看这一年是否是4的倍数,如果是4的倍数就是闰年,如果不是4的倍数就是平年。而遇到整百整千的数字,则必须是400的倍数才是闰年。 21教育网
2014÷4=503……2 2014不是4的倍数,是平年
2008÷4=502 2008是4的倍数,是闰年
2016÷4=504 2016是4的倍数,是闰年
从上面的分析得出2014年是平年,所以这应该是2014年的二月份日历。
(2)李叔叔从二月一日开始休假,假期正好是三个月,应该是2月、3月和4月,2月有28天,3月是大月,有31天,4月是小月,有30天。我们把这3个月的天数加在一起,就是李叔叔假期的总天数:21cnjy.com
28+31+30=89(天)
(3)“妇女节”是3月8日,从日历我们看到2月28日是星期一,那么3月1日就是星期二,8-1=7(天)7÷7=1,从3月1日到3月8日正好过了一周,那么3月8日也是星期二。21·cn·jy·com
解答:
(1)A
(2)28+31+30=89(天)
星期二
【例3】由于帕米尔高原自然环境恶劣,路途艰险难行,守卫祖国边疆的战士们与家里人的书信联系非常困难,邮车也要15天才能来一次,如果邮车在2015年2月1日来到了边防站,那么2016年邮车第一次到达边防站是哪一天(大雪封山等特殊情况忽略不计)?2·1·c·n·j·y
解析:
因为2015÷4=503……3,所以2015年是平年,这一年的2月有28天。我们可以把2月至12月的天数加起来,从而计算出从2015年2月1日到2015年年底有多少天。按平均每个月30天算,再加上6个大月少加的6天,减去2月份多加的2天,减去2月1日这一天,30×11+6-2-1=333(天)。
邮车15天来一次,333÷15=22(次)……3(天),我们可以得出结论,邮车在2015年最后一次来边防站之后还余3天,15-3=12(天),过了2015年底,再有12天,邮车就会到达边防站,所以,2016年邮车第一次到边防站是1月12日。【来源:21·世纪·教育·网】
解答:
2016年1月12日。
【例4】
解析:
要判断这条路能否在国庆节之前修完,需要先算出修这条路需要几天,然后再与9月26日到国庆节的天数相比较。9月是小月,所以只有30天,从9月26日到9月30日的天数为:30-26=4(天),因为9月26日已经开始在修路了,所以要算上这一天,4+1=5(天)。而修路队每天可以修600米,修2000米需要的天数为:2000÷600=3(天)……200(米) 3+1=4(天)再通过比较可以知道国庆节前可以修完这条路。21·世纪*教育网
解答:
30-26=4(天)
4+1=5(天)
2000÷600=3(天)……200(米)
3+1=4(天)
5﹥4
答:国庆节前可以修完这条路。
第二单元 乘法
【例1】仔细观察下面的算式,你能发现什么规律?你能根据这个规律直接写出下面各题的得数吗?
(1)34×11=374
(2)63×11=693
(3)245×11=2695
(4)72×11=__________
(5)618×11=__________
解析:
通过计算、观察可以发现,一个数与11相乘,所得的结果就是将这个数的首位与末位拉开分别作为积的最高位和最低位,再依次将这个数相邻两位由个位加起,和写在十位、百位……www-2-1-cnjy-com
(1)把4写在个位上,3与4的和是7写在十位上,3写在百位,得出34×11=374。
(2)把3写在个位上,6与3的和是9写在十位上,6写在百位,得出63×11=693。
(3)把5写在个位上,4与5的和是9写在十位上,2与4的和是6写在百位上,2写在千位,得出245×11=2695。www.21-cn-jy.com
(4)72×11也用同样的方法:把2写在个位,7与2的和是9写在十位,7写在百位,得出72×11=7922-1-c-n-j-y
(5)618×11,把8写在个位,1与8的和是9写在十位,6与1的和是7写在百位,6写在千位,得出618×11=679821*cnjy*com
解答:
(4)72×11=792
(5)618×11=6798
【例2】下面竖式中,相同的汉字代表相同的数字,不同的汉字代表不同的数字。请求出这些汉字所代表的数字。【来源:21cnj*y.co*m】
甲( ) 乙( )
丙( ) 丁( )
解析:
4的乘法口诀的末尾数字可能为:0,2,4,6,8, 甲位于整个算式乘积的末位,所以甲有可能是0,2,4,6,8,甲乘4没有满十进位,又因为甲在第一个因数的首位不可能是0,所以甲只能是2。则丁与4的乘积末位数为2,3×4=12或8×4=32,那么丁有可能是3或者8,丁是整个算式乘积的第一位数,甲×4=2×4=8,所以丁不可能是3,只能是8。因为丁是8,证明乙乘4没有向前一位进位,那么乙乘4的积不满十,乙有可能是1或者2,甲是2,乙只能是1。丙就是7,
丙×4=7×4=28,加上后面进上来的3正好是31,向前一位进3,乙×4=1×4=4,4+3=7。因数=甲乙丙丁=2178,积=丁丙乙甲=8712【出处:21教育名师】
解答:
【例3】超市新运来25箱苹果,每箱应该是30千克,可是其中一箱在运输途中破损丢失了12千克,你知道超市这一批一共运来多少千克苹果吗?
解析:
方法一:每箱苹果有30千克,我们可以先求出25箱苹果一共多少千克,然后再减去丢失的12千克。
方法二:25箱苹果,有一箱是破损的,少了12千克,还剩30-12=18(千克),其余的24箱,每箱是30千克,一共有30×24=720(千克),再加上18千克,就是这批苹果的总重量。【版权所有:21教育】
解答:
方法一: 30×25-12 方法二:30-12=18(千克)
= 750-12 30×24+18
= 738(千克) = 720+18
= 738(千克)
答:这批苹果一共有738千克。
【例4】你知道这头大象的体重是多少千克吗?
解析:
小猫的体重是2千克,熊猫体重是小猫的15倍,那熊猫的体重就是2×15=30(千克)大象的体重是熊猫的45倍还多36千克,那么大象的体重就是30×45+36=1386(千克)21教育名师原创作品
解答:
2×15×45+36
= 30×45+36
= 1350+36
= 1386(千克)
答:大象的体重是1386千克。
【例5】两名老师带着168名同学去春游,租了5辆车,前四辆车每辆车坐了35人,最后一辆车需要坐多少人?21*cnjy*com
解析:
在计算这个问题时,要注意不要漏算了两位老师,春游的总人数是168+2=170(人),前四辆车每车坐35人,一共可以乘坐35×4=140(人),剩下的人都要坐到最后一辆车上,还剩170-140=30(人)
解答:
168+2=170(人)
35×4=140(人)
170-140=30(人)
答:最后一辆车要坐30人。
【例6】下面是小动物们去“森林小学”上学时的速度和所用的时间,请你根据表格完成练习。
动物
速度(米/分)
82
69
78
93
时间(分钟)
18
51
32
42
(1)估算一下,每个小动物家到学校大约多少米?
(2)哪个小动物距离学校最远?
解析:
(1)小熊每分钟走82米,从家到学校需要18分钟,那它家到学校的距离应该用算式82×18来计算,根据四舍五入的原则82≈80,18≈20,82×18≈1600(米)
小兔子每分钟走69米,大约是70米,走了51分钟,估算时按50去计算,那么小兔子家到学校的距离为69×51≈3500(米)
小老虎每分钟走78米,大约为80米,走了32分钟,四舍五入为30分钟,那么我们估算小老虎从家到学校用78×32≈2400(米)
小马每分钟走93米,大约为90米,走了42分钟,估算时按40分钟计算,那么小马从家到学校的距离为93×42≈3600(米)
(2)在上一小题中我们已经计算出了每个小动物家与学校的距离,我们通过比较可以得出:3600﹥3500﹥2400﹥1600,可以知道小马家离学校最远。
解答:
(1)82×18≈1600(米)
69×51≈3500(米)
78×32≈2400(米)
93×42≈3600(米)
答:小熊家距离学校大约1600米,小兔子家距离学校大约3500米,小老虎家距离学校大约2400米,小马家距离学校大约3600米。
(2)3600﹥3500﹥2400﹥1600
答:小马家离学校最远。
第三单元 吨的认识
【例1】这几辆卡车能同时通过这座大桥吗?
解析:要判断这三辆卡车能不能同时通过这座大桥,我们需要将三辆卡车的总重量计算出来,第一辆车重量为2吨500千克,第二辆车重1吨350千克,第三辆车重1吨700千克,三辆车共重:2吨500千克+1吨350千克+1吨700千克=5吨550千克,所以,这三辆车不能同时通过这座大桥。
解答:
2吨500千克+1吨350千克+1吨700千克=5吨550千克,
答:这三辆车不能同时通过这座大桥。
【例2】森林里有一头野猪,一头大象,一头犀牛,一共重12吨。已知一头野猪和一头犀牛共重7吨;一犀牛和一头大象共重9吨,问:野猪、大象和犀牛各重多少吨?
解析:
因为根据一头野猪和一头犀牛共重7吨,即野猪+犀牛=7吨,一头犀牛和一头大象共重9吨,即大象+犀牛=9吨,所以就可以知道:野猪+2只犀牛+大象的重量是7+9=16(吨),再根据一头野猪,一头大象,一头犀牛,一共重12吨(野猪+犀牛+大象=12吨),就可以知道一头犀牛重 16—12=4(吨);犀牛和野猪共重7吨,那么野猪的重量是7—4=3(吨);同理,根据大象+犀牛=9吨,可以求出大象的重量为9-4=5(吨)。
解答:
7+9=16(吨)
16-12=4(吨)
7-4=3(吨)
9-4=5(吨)
答:野猪重3吨,犀牛重4吨,大象重5吨。
【例3】果园收获了18箱苹果和25箱梨,每箱苹果50千克,每箱梨42千克,这些水果用一辆载重1吨的汽车两次能运完吗?
解析:
我们首先应该求出水果的总重量,根据题意,苹果是18箱,每箱50千克,则苹果的重量为50×18=900(千克),梨有25箱,每箱42千克,则梨的重量为42×25=1050(千克),苹果和梨共重900+1050=1950(千克)
载重1吨的汽车两次可以运2吨,2吨=2000千克,2000﹥1950,所以用一辆载重1吨的汽车两次可以运完。
解答:
50×18=900(千克)
42×25=1050(千克)
2吨=2000千克
2000﹥1950
答:用一辆载重1吨的汽车两次可以运完。
【例4】发电厂需要运16吨煤,大货车限载6吨,小货车限载4吨,如果每次每辆车都装满,怎样安排能恰好运完16吨煤呢?
限载6吨 限载4吨
解析:我们可以通过下面的表格列出几种安排车辆的方案:
方案
大货车(辆)
小货车(辆)
载重总量(吨)
方案一
0
4
16
方案二
1
3
18
方案三
2
1
16
方案四
3
0
18
通过上面的表格,我们可以看出,方案一和方案四在每辆车每次都装满的情况下,正好可以运完16吨。
解答:
有两种方案:
(一)安排4辆小货车。4×4=16(吨)
(二)安排2辆大货车,1辆小货车。2×6+4=16(吨)
第四单元 解决问题
【例1】李伯伯家养了7头奶牛,平均每头奶牛每天产20千克牛奶,这些奶牛9月份一共能产多少千克牛奶?
解析:
我们可以先求出7头奶牛每天产奶多少千克,根据提议,平均每头奶牛每天产奶28千克,7头奶牛可以产奶:20×7=140(千克),9月份是小月,只有30天,要求9月份一共能产多少千克牛奶,就是求这些奶牛30天可以产奶多少千克140×30=4200(千克)
解答:
20×7×30
= 140×30
= 4200(千克)
答:这些奶牛9月份一共能产4200千克奶。
【例2】学校操场有一段跑道长80米,东东每天在这段跑道上跑4个来回,他每天跑多少米?
解析:
解答本题的关键在于理解1个来回是分来和回两个80米,4个来回就是在跑道上跑4个2次,4×2=8(次),跑道长80米,则4个来回是80×8=640(米)
解答:
80×4×2
= 320×2
= 640(米)
答:东东每天跑640米。
【例3】
解析:
两只青蛙每天可以吃掉28只害虫,根据这个条件,我们可以计算出每只青蛙每天吃多少只害虫:58÷2=29(只),然后可以求出4只青蛙每天吃掉多少只害虫:29×4=116(只),一星期是7天,116×7=812(只)
解答:
58÷2=29(只)
29×4×7
= 116×7
= 812(只)
答:4只青蛙一星期可以吃掉812只害虫。
【例4】小猴子小松鼠和小熊猫分苹果。
你知道原来一共有多少个苹果吗?
解析:
小松鼠分得剩下的一半多一个,小熊猫得到6个,也就是剩下的一半少一个,那么6+1=7(个),剩下的一半也就是7个,我们可以求出分给小猴子后剩下的有多少个:7×2=14(个)。小猴子分得总数的一半多一个,那么剩下的14个也就是总数的一半少一个,我们可以求出总数的一半为14+1=15(个),然后可以用15×2=30(个)计算出原来一共有30个苹果。
解答:
6+1=7(个)7×2=14(个)14+1=15(个)15×2=30(个)
答:原来一共有30个苹果。
【例5】小松鼠采来一些松果,它把这些松果分成3份,其中两份送给了妈妈,自己留下的一份又分成了4份,3份给了自己的弟弟妹妹们,自己只剩下9个,你知道小松鼠一共采来多少个松果吗?
解析:
小松鼠最后自己剩下的一份是9个松果,那么我们可以求出它送给妈妈后自己留下的一份分成的4份一共有多少个松果:9×4=36(个),这是小松鼠把采来的松果分成3份后,其中的一份又36个,我们可以求出3份有多少个:36×3=108(个)
解答:
9×4×3
= 36×3
= 108(个)
答:小松鼠一共采来108个松果。
【例6】打一份630字的文件,王阿姨原来要用9分钟,现在只需6分钟,王阿姨现在每分钟比原来多打多少个字?
解析:
要求王阿姨现在每分钟比原来多打多少个字,我们要求出王阿姨原来每分钟打多少个字,现在每分钟打多少个字。原来打630字需要9分钟,每分钟打的字数为:630÷9=70(个),现在打630字只需要6分钟,每分钟打的字数为:630÷6=105(个)然后用现在每分钟打字的数减去原来每分钟打的字数,105-70=35(个)
解答:
630÷9=70(个)
630÷6=105(个)
105-70=35(个)
答:王阿姨现在每分钟比原来多打35个字。
【例7】学校举行体操比赛,把参赛的选手平均分成4个组,每组淘汰了24人后,剩下的总人数正好相当于原来的一组,一共有多少人参加了体操比赛?
解析:
参加体操比赛的人平均分成了四个组,每组淘汰了24人,4个组一共淘汰了24×4=96(人),剩下的人数正好和原来一组的人数相等,4-1=3(组),那么淘汰的人数就和原来3组的人数相等,96÷3=32(人),可以求出每组有32人,根据题意,可以求出4个组的人数为:32×4=128(人)
解答:
24×4=96(人)
4-1=3(组)
96÷3=32(人)
32×4=128(人)
答:一共有128人参加了体操比赛。
第五单元 长方形和正方形的面积
【例1】用4个边长是2厘米的正方形卡片拼图形,如果拼成一个长方形,长方形的长是( )厘米,宽是( )厘米,它的面积是( )平方厘米;如果拼成一个正方形,拼成的正方形的边长是( )厘米,它的面积是( )平方厘米。
解析:
4个边长是2厘米的正方形卡片拼成长方形,如下图:
从图中可以看出拼成的长方形长是原来正方形的4倍,2×4=8(厘米),宽就是正方形的边长2厘米,长方形的面积=长×宽,2×8=16(平方厘米)。
4个边长是2厘米的正方形卡片拼成正方形,如下图:
从图中可以看出,拼成的正方形的边长是原来小正方形边长的2倍,2×2=4(厘米),正方形的面积=边长×边长,4×4=16(平方厘米)
解答:
用4个边长是2厘米的正方形卡片拼图形,如果拼成一个长方形,长方形的长是( 8 )厘米,宽是( 2 )厘米,它的面积是( 16 )平方厘米;如果拼成一个正方形,拼成的正方形的边长是( 4 )厘米,它的面积是( 16 )平方厘米。
【例2】下面的长方形的面积是多少?(每个小方格表示1平方厘米)
解析:
从图中可以看出,这个长方形的长为5厘米,宽为3厘米,长方形的面积为5×3=15(平方厘米)
【例3】一个边长为10米的正方形花坛,如果这个花坛的的边长扩建到原来的2倍,那么这个花坛的面积比原来增加了多少?
解析:
要知道扩建后的花坛面积比原来增加了多少,需要分别求出花坛扩建前后的面积,这是花坛扩建前后都是正方形,要求正方形的面积,需要知道正方形的边长,正方形的面积=边长×边长,根据题意,这个花坛扩建前的边长为10米,那么扩建前正方形花坛的面积为:10×10=100(平方米)。经过扩建,这个花坛的边长扩大到原来的2倍,10×2=20(米)那么扩建后的面积为:20×20=400(平方米),这个花坛的面积比原来增加了400-100=300(平方米)
解答:
10×10=100(平方米)
10×2=20(米)
20×20=400(平方米)
400-100=300(平方米)
答:这个花坛的面积比原来增加了300平方米。
【例4】如下图,小正方形的边长为3厘米,大正方形的面积是小正方形面积的4倍,大正方形的周长比小正方形的周长多多少厘米?
解析:
我们要比较大正方形的周长比小正方形的周长多多少,要先分别求出两个正方形的周长,小正方形的边长在题目中已经告诉我们是3厘米,我们可以直接求出小正方形的周长为3×4=12(厘米),根据题意,大正方形的面积是小正方形面积的4倍,小正方形的面积=3×3=9(平方厘米),大正方形的面积=9×4=36(平方厘米),因为36=6×6,我们可以判断出大正方形的边长为6厘米,那么大正方形的周长为:6×4=24(厘米),然后用大正方形的周长减去小正方形的周长:24-12=12(厘米)
解答:
3×4=12(厘米)
3×3=9(平方厘米)
9×4=36(平方厘米)
36=6×6 大正方形的边长为6厘米。
6×4=24(厘米)
24-12=12(厘米)
答:大正方形的周长比小正方形的周长多12厘米。
【例5】一个长方形的周长是50分米,如果长方形的长是20分米,那么这个长方形的面积是多少平方米?
解析:
长方形的周长=(长+宽)×2,那么,长方形的宽=周长÷2-长,根据这个公式,我们可以求出长方形的宽为:50÷2-20=5(分米),这个长方形的面积为:长方形的面积=长×宽=20×5=100(平方分米),我们知道平方米和平方分米之间的进率为100,100平方分米=1平方米。
解答:
50÷2-20=5(分米)
20×5=100(平方分米)
100平方分米=1平方米
答:这个长方形的面积为1平方米。
【例6】学校有一个长15米,宽8米的长方形花坛,准备在花坛四周修建一条1米宽的小路,小路的面积是多少平方米?
解析:
沿着花坛四周修建了一条小路后,小路的外侧边沿又形成了一个大的长方形,小路的面积等于大长方形的面积减去长方形花坛的面积,花坛的面积为:长方形面积=长×宽=15×8=120(平方米);大长方形的长等于花坛的长加上小路宽度的两倍,也就是15+1+1=17(米),大长方形的宽等于花坛的宽加上小路宽度的两倍,也就是8+1+1=10(米)。大长方形的面积为:17×10=170(平方米)。然后用大长方形的面积减去长方形花坛的面积,就是小路的面积:170-120=50(平方米)
解答:
15×8=120(平方米)
15+1+1=17(米)
8+1+1=10(米)
17×10=170(平方米)
170-120=50(平方米)
答:小路的面积为50平方米。
第六单元 分数的初步认识
【例1】两条同样长的绳子,第一条剪去了,第二条剪去了,哪一条剪去的长一些?
解析:
两条绳子同样长,第一条剪去了,第二条剪去了,我们可以通过比较这两个分数的大小来判断哪一条绳子剪去的长一些,和分子相同,分母不同,比较分子相同的分数大小,分母越小,分数越大,所以>,第一条绳子剪去的更长一些。
解答:
>,第一条绳子剪去的更长一些。
【例2】小兔子和小猴子摘了一个大西瓜,平均切成了九块。
这个西瓜吃完了吗?
解析:
(一)小猴子吃了西瓜的,小兔子吃了西瓜的,我们可以求出它们一共吃了这个西瓜的几分之几,+=,当分子分母相同时这个分数等于1,所以,这个西瓜吃完了。
(二)我们还可以这样想,这个西瓜平均切成了9块,小猴子吃掉了这个西瓜的,也就是吃掉了6块,小兔子吃掉了这个西瓜的,也就是吃掉了3块,它们一共吃掉了6+3=9(块),这个西瓜正好吃完。
解答:
+==1
答:这个西瓜吃完了。
【例3】写出下面阴影部分表示的分数。
(1) (2)
( ) ( )
解析:
(1)这个图形的整体也就是“单位1”是大正方形,我们可以看做把大正方形平均分成9个小正方形,阴影部分由一个小正方形和两个三角形组成,两个小三角形可以拼成一个小正方形,如图:
那么,阴影部分也就是两个小正方形,也就是大正方形的。
(2)整个图形由两个圆组成,阴影部分又分为两块,大的半圆相当于把大圆平均分成2份,占其中的一份,小的半圆相当于把小圆平均分成2份,占其中的一份,那么阴影部分就等于把这两个圆平均分成2份,占其中的一份,也就是。
解答:
(1) (2)
【例4】妈妈买了两块同样的蛋糕,把其中的一块平均分成6小块,爸爸吃了1小块,妈妈也吃了1小块。把另一块平均分成3小块,小雨吃了其中的1小块。哪一块剩下的多?
解析:
根据题意,妈妈把其中一块蛋糕平均分成8小块,爸爸吃了1块,妈妈也吃了1块,那么还剩8-1-1=6(块),剩下的4块占这块蛋糕的,另一块同样大小的蛋糕被分成了4块,小雨吃了其中的1块,剩下3块,剩下的占整个蛋糕的,如下图:
我们可以从图中看出,=,所以,这两块蛋糕剩下的部分同样多。
解答:
这两块蛋糕剩下的部分同样多。
第七单元 小数的初步认识
【例1】爸爸买了一瓶色拉油,连瓶共重3.4千克,用去一半油后连瓶重1.9千克,你知道这瓶油原来有多少千克?瓶有多重?
解析:
这瓶色拉油刚买来时,连瓶重3.4千克,用去一半后连瓶重1.9千克,用去了3.4-1.9=1.5(千克),也就是说,这瓶色拉油的一半是1.5千克,那这瓶色拉油的重量为:1.5+1.5=3(千克),瓶+色拉油=3.4,那么瓶子的重量为:3.4-3=0.4(千克)
解答:
3.4-1.9=1.5(千克)
1.5+1.5=3(千克)
3.4-3=0.4(千克)
答:这瓶油原来重3千克,瓶子重0.4千克。
【例2】用数字6,2,8和小数点可以组成哪些没有重复数字的一位小数(每个数字都用上)?这些小数中最大的是多少?最小的是多少?
解析:
这里有3个数字,分别是6,0,8,用这几个数字组成一位小数, 小数部分为6的数字有:82.6, 28.6;小数部分是8的数字为:62.8, 26.8;小数部分为2的数字有:68.2, 86.2。比较小数的大小,我们应该先比较整数部分,整数部分大的数就大;如果整数部分相同,在比较小数部分,小数部分大的数字就大。我们刚组成的数字整数部分都不同,最大的是86.2,最小的是26.8。
解答:
用数字6,2,8和小数点可以组成哪些没有重复数字的一位小数有:82.6, 28.6, 62.8, 26.8, 68.2, 86.2。
最大的是86.2,最小的是26.8。
【例3】下面是田径运动会中4名运动员在50米赛跑中的成绩,你能帮他们按从快到慢的顺序排一排名次吗?
姓名
小红
小明
小丽
小军
成绩/秒
8.9
7.9
8.2
7.8
解析:
本题中要给这些运动员按从快倒慢的顺序排名次,要比较他们的成绩,成绩是用时间来计算的,谁用的时间最短谁跑的最快。在比较这些小数的大小时,我们先比较整数部分,整数部分大的数就大,其中小红和小丽的成绩分别为8.9和8.2,小明和小军的成绩为7.9和7.8,整数部分为8的数字大,再分别比较8.9和8.2的小数部分,2<9,所以8.2<8.9。而7.9和7.8的小数部分,8<9,所以7.8<7.9,我们按从小到大的顺序排列这些数字:7.8<7.9<8.2<8.9,然后我们可以根据这个顺序排出赛跑的名次:第一名:小军;第二名:小明;第三名:小丽;第四名:小红。
解答:
7.8<7.9<8.2<8.9
第一名:小军;第二名:小明;第三名:小丽;第四名:小红。
【例4】写出符合下列要求的小数。
(1)使这个数最大,这个数是( )。
(2)使这个数最接近81,这个数是( )。
(3)使这个数最小,这个数是( )。
解析:
(1)要使这个数最大,两个方框里都应该填最大的一位数,也就是9,那么这个数字就是90.9。
(2)最接近81的一位小数有两个,一个是80.9,一个是81.1,现在这个小数的个位是0,也就只能是80.9。
(3)要使这个数最小,这两个方框里都应该写最小的一位数,0不能写在首位,那么这个数为10.0
解答:
(1)90.9 (2)80.9 (3)10.0
【例5】一支铅笔0.6元,比一个文具盒便宜8.5元,小明买一支铅笔和一个文具盒,10元够吗?
解析:
首先我们可以求出一个文具盒多少元,根据题意,一支铅笔0.6元,比一个文具盒便宜8.5元,也就是说,一个文具盒比一支铅笔多用8.5元钱,一个文具盒的价格为:0.6+8.5=9.1(元)。然后求出一支铅笔盒一个文具盒一共用多少钱,9.1+0.6=9.7(元),10>9.7,所以小明带了10元够了。
解答:
0.6+8.5=9.1(元)
9.1+0.6=9.7(元)
10>9.7
答:10元钱够了。
【例5】下面是妈妈到超市购物的一张票据。
欢迎光临红星超市
流水号:000120456
收款台:001 收银员:0150
商品名称 数量 单价 总额
可乐 1 2.5 2.5
饼干 1 6.9 6.9
应收金额:
现金:
交易找零:0.6
(1)应收金额是多少?
(2)妈妈付给收银员多少钱?
解析:
(1)应收金额是妈妈购买的所有商品的价格之和,妈妈买了两件商品,一瓶可乐,用去2.5元,一盒饼干用去6.9元,一共用了2.5+6.9=9.4(元),应该付9.4元。
(2)根据上面计算的结果,妈妈应付9.4元,从图表中可以看到,找零0.6元,应付金额加上找零就是妈妈付给收银员的金额,9.4+0.6=10(元)
解答:
(1)2.5+6.9=9.4(元)
答:应付金额是9.4元。
(2)9.4+0.6=10(元)
答:妈妈付给收银员10元。
【例6】买玩具。
5.4元 18.2元 9.9元 15元
(1)买一根跳绳和一个玩具熊一共多少钱?
(2)玩具汽车比玩具熊贵多少钱?
(3)小丽有30元钱,想买两件玩具,可以怎么买?
解析:
(1)一根跳绳5.4元,一个玩具熊9.9元,根据题意可以求出这两种玩具一共用多少钱:5.4+9.9=15.3(元)。
(2)一辆玩具汽车18.2元,一个玩具熊9.9元,求玩具汽车比玩具熊贵多少元,可以用玩具汽车的价格减去玩具熊的价格:18.2-9.9=8.3(元)。
(3)小丽有30元,想买两件玩具,那么她买的两件玩具的价格总和不能超过30元,这里价钱比较贵的两件玩具是小汽车和篮球,这两种玩具的价格总和为:18.2+15=33.2(元),已经超过了30元,所以不能买这两种玩具,其他两种玩具都不超过10元,所以可以随意搭配,比如:买一根跳绳和一个篮球;买一辆玩具小汽车和一个玩具熊;买一个篮球和一个玩具熊等等。
解答:
(1)5.4+9.9=15.3(元)。
答:买一根跳绳和一个玩具熊一共15.3元。
(2)18.2-9.9=8.3(元)
答:玩具汽车比玩具熊贵8.3元。
(3)买一根跳绳和一个篮球:5.4+15=20.4(元)(答案不唯一)
答:可以买一根跳绳和一个篮球,用去20.4元。
第八单元 认识方向
【例1】小明想给来学校参观的客人画一个简单的平面图,你能帮帮他吗?
解析:
我们在画平面示意图时,通常按照“上北下南,左西右东”的原则,根据这个原则,以教学楼为观测点,确定“东西南北”四个方向,然后根据题目的叙述就可以绘制出平面图。
解答:
【例2】蜗牛和蚂蚁要去甲壳虫家。
(1)蜗牛先向( )走( )米,再向( )走( )米,就到达甲壳虫家。
(2)蚂蚁先向( )走( )米,再向( )走( )米,就到达甲壳虫家。
解析:
(1)小蜗牛有两条路线,第一条:它要先向西走一个格,也就是2米,再向北走三个格,也就是6米。第二条:它先向北走三个格,也就是6米,然后再向西走一个格,也就是2米。
(2)给小蚂蚁画的路线中,也有两条,第一条:蚂蚁先向东走2格,也就是4米,再向北走2格,也就是4米,就可以到达甲壳虫家。第二条:它要先向西走1格,也就是2米,再向北走1格,也就是2米,再向东走1格,也是2米,再向北走1格,也就是2米,再向东走2格,也就是4米到达甲壳虫家。
解答:
(1)西,2,北,6(答案不唯一)
(2)东,4,北,4
【例3】帮助小动物找家.
(1)森林公园的东北角住着小花猫. (2)小羊住在森林公园的东面.
(3)小羊的南面住着小兔. (4)小花猫的西面住着小鹿.
(5)森林公园的西南角住着小牛. (6)小牛的东面住着小猪.
(7)熊猫住在小牛的北面. (8)狐狸住在熊猫的北面.
解析:
我们首先以“森林公园”为观测点,小羊住在森林公园的东面(右东),确定小花猫在森林公园的东北方向(示意图右上角),小牛住在森林公园的西南角(示意图左下角);然后再以小羊家为观测点,确定小兔的位置是在小羊的南面(小羊下面)。以小花猫家为观测点,小鹿在小花猫西面(小花猫左面)。再以小牛家为观测点,小牛家的东面住着小猪(小牛右面),熊猫家在小牛家的北面(小牛的上面)。以熊猫家为观测点,确定狐狸家住在熊猫家的北面(熊猫上面)
解答:
【例4】在括号里填上正确的方向。
(1)男孩前面是( ),左面是( ),右面是( )。
(2)如果男孩转向他的左手方向,那他前面是( ),后面是( )。
解析:
(1)这个男孩的背面是西,前面是和西相反的方向,就是东方,左面是北,右面是南。
(2)如果男孩转向的他的左手方向,他的左边是北,那么现在他面对着北方,后面就是南方。
解答:
(1)东, 北, 南
(2)北, 南
【例5】小晴从家出发向北走100米到学校,小晴家在哪里?图中( )表示小晴家。(填字母)
解析:
根据题意,小晴从家出发向北走100米到达学校,我们来观察A、B、C三个点,A点到学校需要向西走100米,所以A点不是小晴的家,C点到学校需要先向北走100米,然后再向西走100米,所以C点不是小晴的家,只有在B点是向北走100米到达学校,所以B点是小晴的家。
解答:
图中(B)表示小晴家。
第九单元 整理数据
【例1】下面是三年级一班同学们9月份作业得星情况记录单,请你帮老师整理一下这些数据吧。
(1)整理记录单中的数据,把得到的结果填入统计表中,并根据统计表回答问题。
得星等级
A(60~80)
B(40~59)
C(20~39)
D(0~19)
人数
(2)得星数在40颗以上的是良好,良好的学生有多少人?
(3)你还能提出什么数学问题?
(4)你认为D等级的同学应该怎样做呢?
解析:
得星等级
A(60~80)
B(40~59)
C(20~39)
D(0~19)
人数
一
(1)这是一份学生作业得星情况的记录单,通过观察记录单我们可以发现,得星最多的是75颗,最少的是14颗,然后统计表将得星情况按每20颗一段进行统计整理。在整理数据时,要按先后顺序逐个统计,每个数据在哪个等级,可以先用画“正”字的方法在那个等级画上一笔,这样可以避免重复或遗漏。统计之后还要数一数统计的总人数是否与记录单的总人数相等。
得星等级
A(60~80)
B(40~59)
C(20~39)
D(0~19)
人数
8
11
8
3
(2)得星数在40颗以上的是良好,那么良好包括两个等级:A等级和B等级,A等级有8人,B等级有11人,那么良好的人数为:8+11=19(人)
(3)根据统计表可以提出很多数学问题,比如:得星数在40颗以下的有多少人?
得星数在40颗以下的包括C等级和D等级,一共有:8+3=11(人)
(4)D等级是得星数最少的同学,可以建议他们认真完成作业,严格要求自己,遇到不明白的问题向老师、同学、家长求教等等。
解答:
(1)
(2)8+11=19(人)
得星等级
A(60~80)
B(40~59)
C(20~39)
D(0~19)
人数
8
11
8
3
答:良好的人数为19人。
(3)得星数在40颗以下的有多少人?
8+3=11(人)
答:得星数在40颗以下的有11人.
(4)我建议D等级的同学,上课认真听讲,课下严格按老师的要求完成作业,遇到不明白的问题主动寻求老师、同学或家长的帮助。
第十单元 数学百花园
【例1】植树节学校组织家长和孩子们去植树,1组有3名家长和5名同学,共植树22棵,2组有5名家长和5名同学共植树30棵树,如果每个家长植树的数目相同,每名同学植树的数目也相同,你能计算出每个家长植树多少棵,每个同学植树多少棵吗?
解析:
我们可以将题中的数量关系转化成文字算式,进行比较:
1组:3名家长植树棵树+5名同学植树棵树=22棵
2组:5名家长植树棵树+5名同学植树棵树=30棵
从上面的文字关系式中,我们可以推算出,相差的8棵树就是2名家长植树的棵数。也就是说2名家长植树8棵。
我们可以求出每名家长植树的棵数:8÷2=4(棵)
然后可以求出1组的三名家长植树棵树为:4×3=12(棵)
1组一共植树22棵,减去家长植的12棵,剩下的就是5名同学植树的棵数:22-12=10(棵)
然后我们就可以求出每名同学植树的棵数:10÷5=2(棵)
解答:
5-3=2(名)
8÷2=4(棵)
4×3=12(棵)
22-12=10(棵)
10÷5=2(棵)
答:每名家长植树4棵,每名学生植树2棵。
【例2】明明、欣欣和乐乐一起去买水果,明明买了8个苹果、6个橘子和3个桃子共用去36元,欣欣买了5个苹果、6个橘子和3个桃子共用去27元,乐乐买了5个苹果和6个橘子用去21元,你知道每种水果的单价是多少吗?
解析:
明明买的水果:
8个苹果+6个橘子+3个桃子=36元
欣欣买的水果:
5个苹果+6个橘子+3个桃子=27元
通过比较我们发现,明明只比欣欣多买了3个苹果,他比欣欣多用了36-27=9元钱,也就是说3个苹果用去9元钱,每个苹果用9÷3=3(元)
乐乐比欣欣少买了3个桃子,少用了27-21=6(元)钱,这6元就是3个桃子的价格,每个桃子价格为:6÷3=2(元)
然后我们计算乐乐买了5个苹果用去的钱数:5×3=15(元)
乐乐一共用了21元,从21元中减去买苹果的15元,就是买6个橘子用去的钱数:21-15=6(元)6÷6=1(元)每个橘子1元钱。
解答:
8-5=3(个)36-27=9(元)9÷3=3(元)
27-21=6(元)6÷3=2(元)
5×3=15(元)21-15=6(元)6÷6=1(元)
答:苹果:3元 橘子:1元 桃子:2元
【例3】粮店运来一批粮食,4袋大米和5袋面粉共重300千克,2袋大米和3袋面粉共重170千克,一袋大米和一袋面粉各重多少千克?
解析:
我们先把题目中的条件转化成文字式进行观察:
4袋大米+5袋面粉=300千克
2袋大米+3袋面粉=170千克
上面的算式中大米的数量和面粉的数量都不相同,但是我们发现,第一个算式中大米的数量是第二个算式中数量的2倍,那么我可以将第二个算式中大米和面粉的数量都乘2:4袋大米+6袋面粉=340千克。
然后再比较两个算式:
4袋大米+5袋面粉=300千克
4袋大米+6袋面粉=340千克
两个算式只相差6-5=1(袋)面粉,相差的重量为:340-300=40(千克),可以算出一袋面粉的重量为40千克。
然后我们再计算3袋面粉的重量:40×3=120(千克)
2袋大米的重量为:170-120=50(千克)
每袋大米重:50÷2=25(千克)
解答:
170×2-300=40(千克)
40×3=120(千克)
170-120=50(千克)
50÷2=25(千克)
答:每袋大米重25千克,每袋面粉重40千克。
【例3】用一个杯子向空瓶里倒水,如果倒进3杯水,连瓶共重440克;如果倒进5杯水,连瓶共得600克。那么,一杯水与一个空瓶共重多少千克?
解析:
3杯水+瓶=440克 (1)
5杯水+瓶=600克 (2)
我们可以比较:为什么(1)(2)两个算式相差了600-440=160克。因为两个算式相差了2杯水,也就是2杯水的重量为160克。
我们可以求出1杯水的重量为:160÷2=80(克)
那么3杯水重量为:80×3=240(克)
空瓶的重量为:440-240=200(克)
解答:
600-440=160(克)
160÷2=80(克)
80×3=240(克)
440-240=200(克)
答:一杯水的重量为80克,一个空瓶的重量为200克。
【例4】星期天,小丽要做完下面表格中的这些事,最少需要多少分钟?
洗碗
收拾客厅
拿衣服去洗
拖地
洗衣机洗衣服
晾衣服
5分钟
12分钟
1分钟
10分钟
30分钟
5分钟
解析:
要想用最少的时间完成这些事情,能同时做的事情尽量同时做,比如在洗衣机洗衣服时小丽可以去洗碗、收拾客厅、拖地,这样就可以节约出一部分时间。小丽可以像下面示意图那样去安排时间:
解答:
1+30+5=36(分钟)
答:小丽最少需要36分钟。
【例5】小梅、小晴、小娟同时来到医务室,小梅看牙需要7分钟,小晴量体温需要5分钟,小娟拿药需要4分钟,怎样合理安排他们的治疗顺序,使她们等候时间总和最少,他们一共要用多少时间?
解析:
要想让等候时间总和最少,要按所用时间从短到长的顺序来安排,也就是先让用时最少的小娟拿药,她需要4分钟,另外两个人需要各等4分钟;然后让小晴量体温,她需要5分钟,小梅需要再等5分钟;最后让小梅看牙,她需要7分钟,她们各自用的时间为:
小娟:4分钟(拿药)
小晴:4分钟(等候)+5分钟(量体温)=9分钟
小梅:4分钟(等候)+5分钟(等候)+7分钟(看牙)=16分钟
那她们用的时间总和为:4+9+16=29(分钟)
解答:
先让小娟拿药,然后小晴量体温,最后小梅看牙。
小娟:4分钟(拿药)
小晴:4分钟(等候)+5分钟(量体温)=9分钟
小梅:4分钟(等候)+5分钟(等候)+7分钟(看牙)=16分钟
那她们用的时间总和为:4+9+16=29(分钟)
答:她们用的时间总和为29分钟。
