数学五年级下北京课改版提升-爬坡试题(含解析)
文档属性
| 名称 | 数学五年级下北京课改版提升-爬坡试题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 515.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-12 00:00:00 | ||
图片预览


文档简介
北京版5年级数学下册-爬坡题
第一单元 长方体和正方体
例1:有一个长60厘米、宽50厘米、高30厘米的长方体木箱,按照下图的方式用绳子捆扎这个长方体木箱,绳子总长多少米?(接头处忽略不计。)
解析:把绳子分成三类,长度分别与长方体的长、宽、高相等。由图可知,与长相等的绳子有4根(上、下、前、后面各有1根);与宽相等的绳子有6根(上下面各有2根,左右面各有1根);与高相等的绳子有6根(前后面各有2根,左右面各有1根),所以绳子的总长=长×4+宽×6+高×6。
解答:60×4+50×6+30×6=720(厘米)=7.2(米)
答:绳子的总长7.2米。
例2:一个长方体的木块,正好截成了3个完全相同的正方体木块,这3个小正方体的棱长总和比原来长方体棱长总和增加了160厘米,求原长方体的长、宽、高分别是多少?
解析:如图,一个长方体木块被截成3个完全相同的正方体木块后,多了(3-1)×2=4(个)正方形的截面。每个截面上有4条棱,共多了4×4=16(条)棱。由于棱长总和增加了160厘米可知,每条棱长为160÷16=10(厘米),原来长方体的宽=原来长方体的高=小正方体的棱长=10(厘米)。原来长方体的长是小正方体棱长的3倍,即10×3=30(厘米)。
解答:160÷(4×4)=10(厘米) 10×3=30(厘米)
答:原来长方体的长是30厘米,宽10厘米,高10厘米。
例3:把一个长6厘米,宽5厘米,高4厘米的长方体切成两个完全相同的长方体后,表面积最多增加多少平方厘米?最少增加多少平方厘米?
解析:长方体按图一放置,因为原长方体上下两个面的面积最大,所以切后表面积增加最多,截面应该与上、下两个面平行,如图二;因为原长方体左右两个面的面积最小,所以切后表面积增加最少,截面应该与左右两个面平行,如图三。切一次,截口处有两个相同的截面,所以增加的面积为每个截面面积的2倍。
图一 图二 图三
解答:最多增加:6×5×2=60(平方厘米)
最少增加:4×5×2=40(平方厘米)
答:表面积最多增加60平方厘米,最少增加40平方厘米。
例4:如下图,求这个机器零件的表面积。(单位:厘米)
解析:可以设想把A面向上平移到与上面平齐,把B面向右平移到与右面平齐,把C面向前平移到与前面平齐,原零件的表面积与平移后的形成的长方体的表面积相等。因此只需求出新形成的长方体的表面积就可以了。
解答:(5×8+8×6+5×6)×2=236(平方厘米)
答:这个零件的表面积是236平方厘米。
例5:把一个2米长的长方体木料平行于侧面截成相同的3段,表面积比原来增加了12平方分米,这个木料原来的体积是多少?
解析:如图所示,把这个长方体木料平行于侧面截成相同的3段,增加了4个截面,每个截面的面积是12÷4=3(平方分米)。因此长方体的体积=截面的面积×长方体的长,即2米=20分米,20×3=60(立方分米)
解答:2米=20分米 20×(12÷4)=60(立方分米)
例6:一块长方形铁皮(如图),从四个角各切掉一个边长为5厘米的正方形,然后做成盒子,这个盒子的容积是多少升?
解析:由题意可知,盒子的长90-5×2=80(厘米),宽是60-5×2=50厘米,高5厘米,长方体的容积=长×宽×高,把数据代入公式即可解答。
解答:(90-5×2)×(60-5×2)×5=20000(立方厘米)=20(升)
第二单元 折线统计图与可能性
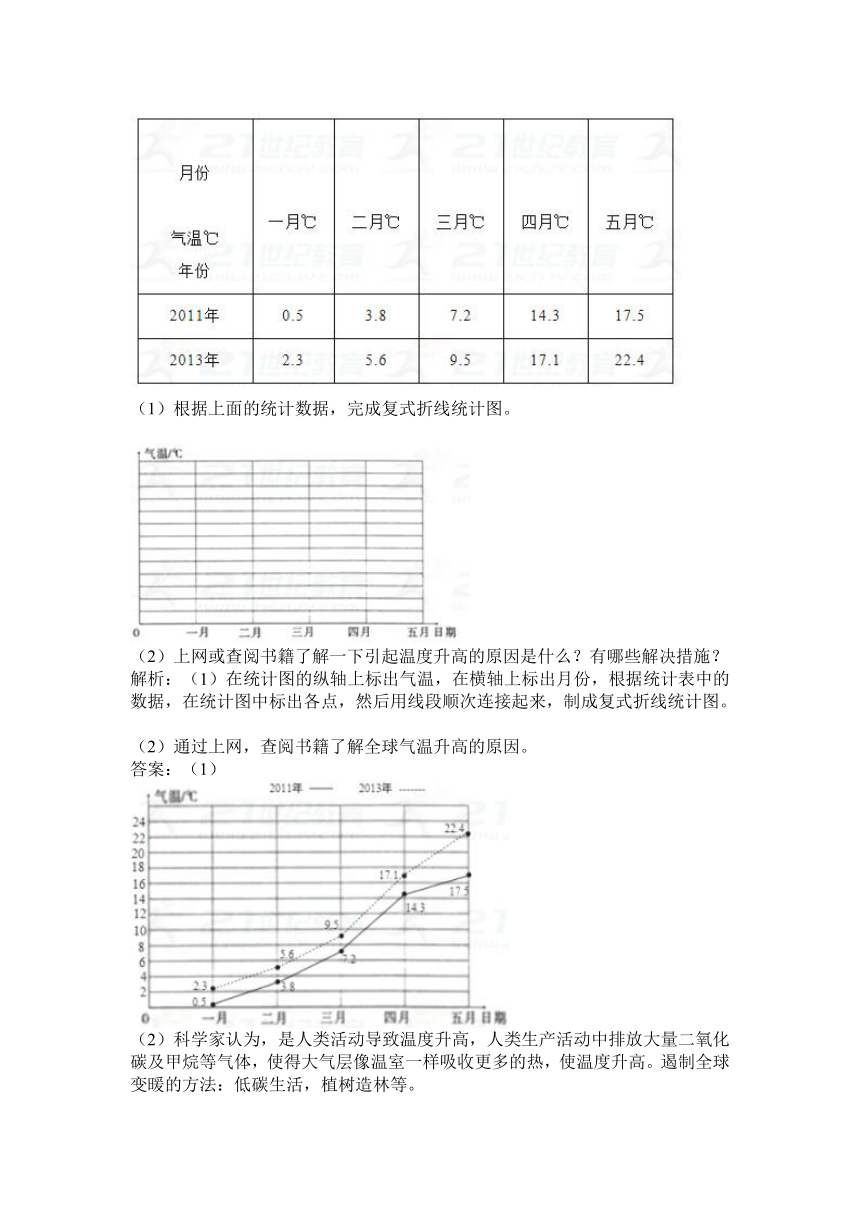
例1:下面是某市2011年和2013年一至五月月平均气温统计表。
根据上面的统计数据,完成复式折线统计图。
(2)上网或查阅书籍了解一下引起温度升高的原因是什么?有哪些解决措施?
解析:(1)在统计图的纵轴上标出气温,在横轴上标出月份,根据统计表中的数据,在统计图中标出各点,然后用线段顺次连接起来,制成复式折线统计图。
通过上网,查阅书籍了解全球气温升高的原因。
答案:(1)
(2)科学家认为,是人类活动导致温度升高,人类生产活动中排放大量二氧化碳及甲烷等气体,使得大气层像温室一样吸收更多的热,使温度升高。遏制全球变暖的方法:低碳生活,植树造林等。
例2:把梅花4、红桃5、方块7和黑桃8这四张扑克牌反口在桌面上,与你的同桌做游戏,请你设计个公平的游戏规则。
解析:只要设计成摸到的可能性都相等即可:因为4、5、7、8的扑克牌各一张,其中偶数点有4、8两张,奇数有5、7两张,,每次摸一张牌是偶数的甲赢,是奇数乙赢,可能性各占一半。
解答:因为4、5、7、8的扑克牌各一张,其中偶数点有4、8两张,奇数有5、7两张,,每次摸一张牌是偶数的甲赢,是奇数乙赢,可能性各占一半,对双方都公平。
第三单元 因数和倍数
例1:五个连续奇数的和是155,其中最大的数是多少?
解析:因为相邻两个奇数相差2,所以五个连续奇数的中间数一定时这五个数的平均数,由此可知这五个数的中间数是155÷5=31,最大数比中间数多2个2,即最大数是31+2×2=35.
解答:其中最大数是35。
例2:妈妈买来30个苹果,让小明把苹果放入篮子中。要求不能一次拿完,也不能一个一个地拿,而且每次拿的个数相同,最后正好一个不剩。小明共有几种拿法?每种拿法每次可以分别拿几个?
解析:从“每次拿的个数相同,最后正好一个不剩”可以知道每次拿的个数应是30的因数。因为不能一次拿完,也不能一个一个地拿,所以应该去掉1和它本身(即30)这两种拿法。因此,先找出30有多少个因数,用因数的个数减去2就是所求。
解答:30的因数有1、2、3、5、6、10、15、30,共8个因数。8-2=6(种)
答:小明共有6种拿法,每种拿法每次可以分别拿、2、3、5、6、10、15个。
例3:三个不同质数的和是82,这三个质数的积最大是多少?
解析:凡是质数,除2外都是奇数,三个质数相加的和是偶数,一定有一个质数是2.82-2=80,剩下的两个质数的和是80,两个数的差越小,积就越大,这两个质数是43和37时,这三个质数的积最大。
解答:37×43×2=3182
答:这三个质数的积是3182。
第四单元 分数的意义和基本性质
例1:将一根圆木锯成8段,每锯一次所用的时间相同,锯一次用的时间是总时间的几分之几?
解析:解题关键是明确锯成8段共锯了几次。锯一次分成两段,锯2次分成3段……锯7次分成8段,每次锯的时间相同 ,也就是把总时间平均分成了7份,每锯依次所用的时间占一份。
解答:锯一次所用的时间是总时间的。
例2:的分子加上15,要使分数的大小不变,分母应加上( )。
解析:的分子加上15,变成5+15=20,扩大了20÷5=4倍,根据分数的基本性质,要使分数的大小不变,分母也应该扩大4倍,变成6×4=24,所以增加24-6=18.
解答:分母应增加18。
例3:有一张长方形纸,长80厘米,宽60厘米。如果要剪成若干张同样大小的正方形纸且没有剩余,那么剪成的正方形纸的边长最大是多少厘米?
解析:要想剪成若干张同样大小的正方形纸且没有剩余,正方形纸的边长必须既是80的因数,又是60的因数,也就是说必须是80和60的公因数,要想求剪成的正方形的边长最大是多少厘米,实际上就是求80和60的最大公因数是多少。
解答:80和60的最大公因数是2×2×5=20,所以剪成的正方形的边长最大是20厘米。
第五单元 分数的加法和减法
例1:在括号里填上不同的数,使每个分数既是最简分数,又满足等式要求。
++=
解析:要想满足每个分数都是最简分数,每个分数的分子和分母只能有公因数1。因为分母24的质因数有2、3所以分子就不能是2、3的倍数。在1~19中,只有1、5、7、11、13、17、19满足既不是2的倍数,也不是3的倍数。可以把19写成上面的数中3个不同的数的和的形式,19=1+5+13,19=1+7+11,因此分子可以分别为1、5、13或1、7、11。
解答:++=,++=
例2:不用通分,你能很快计算出下面每道题的结果吗?
(1)+++ (2)++++
解析:算式(1)可以用图一表示,算式(2)可以用图二表示。如下图:
观察图一可知,算式(1)的结果是整体1减去阴影部分所对应的分数,即1-=;观察图二可知,算式(2)的结果是整体1减去阴影部分所对应的分数,1-=。
解答:(1)+++=1-= (2)++++=1-=
第六单元 数学百花园
例1:一个棱长为5厘米的正方体,分别在它的前、后、左、右、上、下面的中心位置各挖去一个棱长为1厘米的小正方体后,剩下图形的表面积是多少?
解析:这个剩下图形的表面积是大正方体的面积,加上6个边长为1厘米的小正方体的4个侧面的面积,据此解答即可。
答案:5×5×6+1×1×6×4=174(平方厘米)
例2:++++…+
解析:观察题中的算式,发现:每个分数的分子都是1,分母可以写成两个相邻自然数的乘积,如2=1×2,6=2×3,12=3×4…;然后拆分分数:每个分数都可以写成两个分子都是1,分母是相邻自然数的分数的差的形式,如=1-,=-,=-……;整理算式:原式=(1-)+(-)+(-)+…+(-),通过观察整理后的算式可知,前后两个不同运算符号的分数相加等于0。
解答:++++…+
=(1-)+(-)+(-)+…+(-)
=1-+-+-+…+-
=1-
=
第一单元 长方体和正方体
例1:有一个长60厘米、宽50厘米、高30厘米的长方体木箱,按照下图的方式用绳子捆扎这个长方体木箱,绳子总长多少米?(接头处忽略不计。)
解析:把绳子分成三类,长度分别与长方体的长、宽、高相等。由图可知,与长相等的绳子有4根(上、下、前、后面各有1根);与宽相等的绳子有6根(上下面各有2根,左右面各有1根);与高相等的绳子有6根(前后面各有2根,左右面各有1根),所以绳子的总长=长×4+宽×6+高×6。
解答:60×4+50×6+30×6=720(厘米)=7.2(米)
答:绳子的总长7.2米。
例2:一个长方体的木块,正好截成了3个完全相同的正方体木块,这3个小正方体的棱长总和比原来长方体棱长总和增加了160厘米,求原长方体的长、宽、高分别是多少?
解析:如图,一个长方体木块被截成3个完全相同的正方体木块后,多了(3-1)×2=4(个)正方形的截面。每个截面上有4条棱,共多了4×4=16(条)棱。由于棱长总和增加了160厘米可知,每条棱长为160÷16=10(厘米),原来长方体的宽=原来长方体的高=小正方体的棱长=10(厘米)。原来长方体的长是小正方体棱长的3倍,即10×3=30(厘米)。
解答:160÷(4×4)=10(厘米) 10×3=30(厘米)
答:原来长方体的长是30厘米,宽10厘米,高10厘米。
例3:把一个长6厘米,宽5厘米,高4厘米的长方体切成两个完全相同的长方体后,表面积最多增加多少平方厘米?最少增加多少平方厘米?
解析:长方体按图一放置,因为原长方体上下两个面的面积最大,所以切后表面积增加最多,截面应该与上、下两个面平行,如图二;因为原长方体左右两个面的面积最小,所以切后表面积增加最少,截面应该与左右两个面平行,如图三。切一次,截口处有两个相同的截面,所以增加的面积为每个截面面积的2倍。
图一 图二 图三
解答:最多增加:6×5×2=60(平方厘米)
最少增加:4×5×2=40(平方厘米)
答:表面积最多增加60平方厘米,最少增加40平方厘米。
例4:如下图,求这个机器零件的表面积。(单位:厘米)
解析:可以设想把A面向上平移到与上面平齐,把B面向右平移到与右面平齐,把C面向前平移到与前面平齐,原零件的表面积与平移后的形成的长方体的表面积相等。因此只需求出新形成的长方体的表面积就可以了。
解答:(5×8+8×6+5×6)×2=236(平方厘米)
答:这个零件的表面积是236平方厘米。
例5:把一个2米长的长方体木料平行于侧面截成相同的3段,表面积比原来增加了12平方分米,这个木料原来的体积是多少?
解析:如图所示,把这个长方体木料平行于侧面截成相同的3段,增加了4个截面,每个截面的面积是12÷4=3(平方分米)。因此长方体的体积=截面的面积×长方体的长,即2米=20分米,20×3=60(立方分米)
解答:2米=20分米 20×(12÷4)=60(立方分米)
例6:一块长方形铁皮(如图),从四个角各切掉一个边长为5厘米的正方形,然后做成盒子,这个盒子的容积是多少升?
解析:由题意可知,盒子的长90-5×2=80(厘米),宽是60-5×2=50厘米,高5厘米,长方体的容积=长×宽×高,把数据代入公式即可解答。
解答:(90-5×2)×(60-5×2)×5=20000(立方厘米)=20(升)
第二单元 折线统计图与可能性
例1:下面是某市2011年和2013年一至五月月平均气温统计表。
根据上面的统计数据,完成复式折线统计图。
(2)上网或查阅书籍了解一下引起温度升高的原因是什么?有哪些解决措施?
解析:(1)在统计图的纵轴上标出气温,在横轴上标出月份,根据统计表中的数据,在统计图中标出各点,然后用线段顺次连接起来,制成复式折线统计图。
通过上网,查阅书籍了解全球气温升高的原因。
答案:(1)
(2)科学家认为,是人类活动导致温度升高,人类生产活动中排放大量二氧化碳及甲烷等气体,使得大气层像温室一样吸收更多的热,使温度升高。遏制全球变暖的方法:低碳生活,植树造林等。
例2:把梅花4、红桃5、方块7和黑桃8这四张扑克牌反口在桌面上,与你的同桌做游戏,请你设计个公平的游戏规则。
解析:只要设计成摸到的可能性都相等即可:因为4、5、7、8的扑克牌各一张,其中偶数点有4、8两张,奇数有5、7两张,,每次摸一张牌是偶数的甲赢,是奇数乙赢,可能性各占一半。
解答:因为4、5、7、8的扑克牌各一张,其中偶数点有4、8两张,奇数有5、7两张,,每次摸一张牌是偶数的甲赢,是奇数乙赢,可能性各占一半,对双方都公平。
第三单元 因数和倍数
例1:五个连续奇数的和是155,其中最大的数是多少?
解析:因为相邻两个奇数相差2,所以五个连续奇数的中间数一定时这五个数的平均数,由此可知这五个数的中间数是155÷5=31,最大数比中间数多2个2,即最大数是31+2×2=35.
解答:其中最大数是35。
例2:妈妈买来30个苹果,让小明把苹果放入篮子中。要求不能一次拿完,也不能一个一个地拿,而且每次拿的个数相同,最后正好一个不剩。小明共有几种拿法?每种拿法每次可以分别拿几个?
解析:从“每次拿的个数相同,最后正好一个不剩”可以知道每次拿的个数应是30的因数。因为不能一次拿完,也不能一个一个地拿,所以应该去掉1和它本身(即30)这两种拿法。因此,先找出30有多少个因数,用因数的个数减去2就是所求。
解答:30的因数有1、2、3、5、6、10、15、30,共8个因数。8-2=6(种)
答:小明共有6种拿法,每种拿法每次可以分别拿、2、3、5、6、10、15个。
例3:三个不同质数的和是82,这三个质数的积最大是多少?
解析:凡是质数,除2外都是奇数,三个质数相加的和是偶数,一定有一个质数是2.82-2=80,剩下的两个质数的和是80,两个数的差越小,积就越大,这两个质数是43和37时,这三个质数的积最大。
解答:37×43×2=3182
答:这三个质数的积是3182。
第四单元 分数的意义和基本性质
例1:将一根圆木锯成8段,每锯一次所用的时间相同,锯一次用的时间是总时间的几分之几?
解析:解题关键是明确锯成8段共锯了几次。锯一次分成两段,锯2次分成3段……锯7次分成8段,每次锯的时间相同 ,也就是把总时间平均分成了7份,每锯依次所用的时间占一份。
解答:锯一次所用的时间是总时间的。
例2:的分子加上15,要使分数的大小不变,分母应加上( )。
解析:的分子加上15,变成5+15=20,扩大了20÷5=4倍,根据分数的基本性质,要使分数的大小不变,分母也应该扩大4倍,变成6×4=24,所以增加24-6=18.
解答:分母应增加18。
例3:有一张长方形纸,长80厘米,宽60厘米。如果要剪成若干张同样大小的正方形纸且没有剩余,那么剪成的正方形纸的边长最大是多少厘米?
解析:要想剪成若干张同样大小的正方形纸且没有剩余,正方形纸的边长必须既是80的因数,又是60的因数,也就是说必须是80和60的公因数,要想求剪成的正方形的边长最大是多少厘米,实际上就是求80和60的最大公因数是多少。
解答:80和60的最大公因数是2×2×5=20,所以剪成的正方形的边长最大是20厘米。
第五单元 分数的加法和减法
例1:在括号里填上不同的数,使每个分数既是最简分数,又满足等式要求。
++=
解析:要想满足每个分数都是最简分数,每个分数的分子和分母只能有公因数1。因为分母24的质因数有2、3所以分子就不能是2、3的倍数。在1~19中,只有1、5、7、11、13、17、19满足既不是2的倍数,也不是3的倍数。可以把19写成上面的数中3个不同的数的和的形式,19=1+5+13,19=1+7+11,因此分子可以分别为1、5、13或1、7、11。
解答:++=,++=
例2:不用通分,你能很快计算出下面每道题的结果吗?
(1)+++ (2)++++
解析:算式(1)可以用图一表示,算式(2)可以用图二表示。如下图:
观察图一可知,算式(1)的结果是整体1减去阴影部分所对应的分数,即1-=;观察图二可知,算式(2)的结果是整体1减去阴影部分所对应的分数,1-=。
解答:(1)+++=1-= (2)++++=1-=
第六单元 数学百花园
例1:一个棱长为5厘米的正方体,分别在它的前、后、左、右、上、下面的中心位置各挖去一个棱长为1厘米的小正方体后,剩下图形的表面积是多少?
解析:这个剩下图形的表面积是大正方体的面积,加上6个边长为1厘米的小正方体的4个侧面的面积,据此解答即可。
答案:5×5×6+1×1×6×4=174(平方厘米)
例2:++++…+
解析:观察题中的算式,发现:每个分数的分子都是1,分母可以写成两个相邻自然数的乘积,如2=1×2,6=2×3,12=3×4…;然后拆分分数:每个分数都可以写成两个分子都是1,分母是相邻自然数的分数的差的形式,如=1-,=-,=-……;整理算式:原式=(1-)+(-)+(-)+…+(-),通过观察整理后的算式可知,前后两个不同运算符号的分数相加等于0。
解答:++++…+
=(1-)+(-)+(-)+…+(-)
=1-+-+-+…+-
=1-
=
