18.1.1平行四边形的定义和性质(课件)
文档属性
| 名称 | 18.1.1平行四边形的定义和性质(课件) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-13 09:07:51 | ||
图片预览









文档简介
(共35张PPT)
平行四边形的
定义和性质
人教版 八年级下
一、引言
现实世界中,四边形也在装点着我们的生活。宏伟的建筑物、铺满地砖的地板、别具一格的窗棂、天空飞舞的风筝······处处都有四边形的身影。
一、引言
在小学,我们已经学过一些特殊的四边形,如长方形、正方形、平行四边形和梯形等,这些特殊的四边形与我们的生活关系更为密切。
在本章,我们将进一步认识这些特殊的四边形,分析它们的联系与区别,探索并证明它们的性质及判定方法,进一步提高分析问题、解决问题的能力。
一、引言
二、生活中的四边形
平行四边形是我们常见的图形,小区的伸缩门、庭院的竹篱笆、载重汽车的防护栏,都是平行四边形的形象。
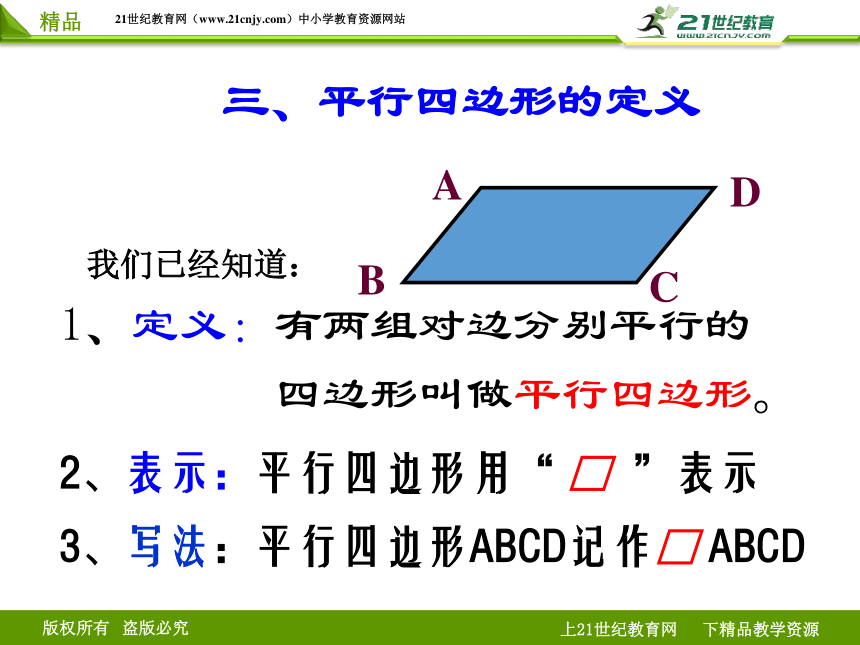
三、平行四边形的定义
我们已经知道:
1、定义:有两组对边分别平行的
四边形叫做平行四边形。
2、表示:平行四边形用“ □ ”表示
3、写法:平行四边形ABCD记作□ ABCD
A
B
C
D
四、平行四边形的性质
由平行四边形的定义,我们知道:
平行四边形的两组对边分别平行。
除此之外,平行四边形还有什么性质呢?
也就是说,它的边、角有什么关系?
量一量,你一定能猜想到的。试试看:
′
四、平行四边形的性质
1、平行四边形的两组对边分别平行。
2、平行四边形的对边相等。
3、平行四边形的对角相等。
我们知道,真命题必须经过证明,才能承认它的正确性。
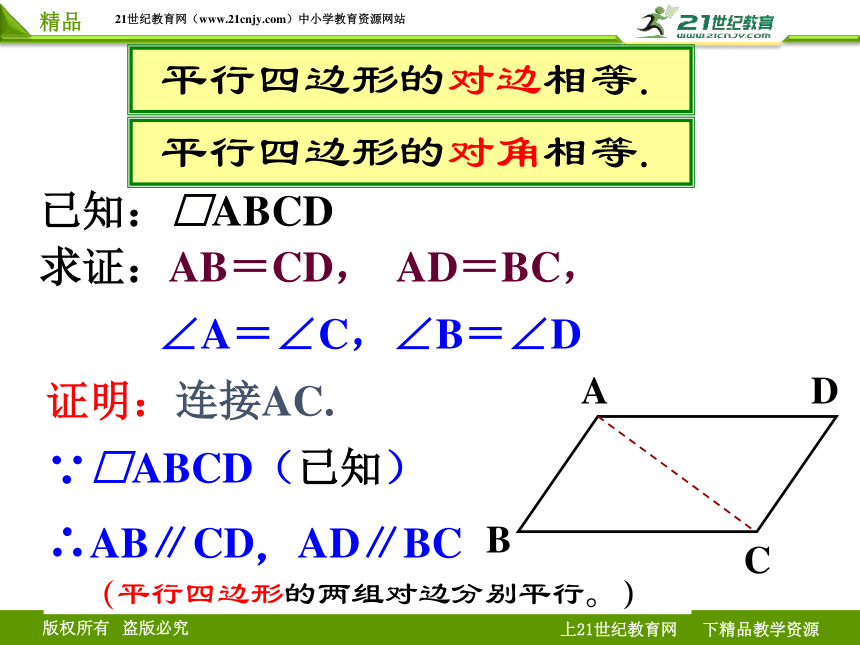
平行四边形的对边相等.
已知:□ABCD
求证:AB=CD, AD=BC,
∠A=∠C,∠B=∠D
A
B
C
D
证明:连接AC.
平行四边形的对角相等.
∵□ABCD(已知)
∴AB∥CD,AD∥BC
(平行四边形的两组对边分别平行。)
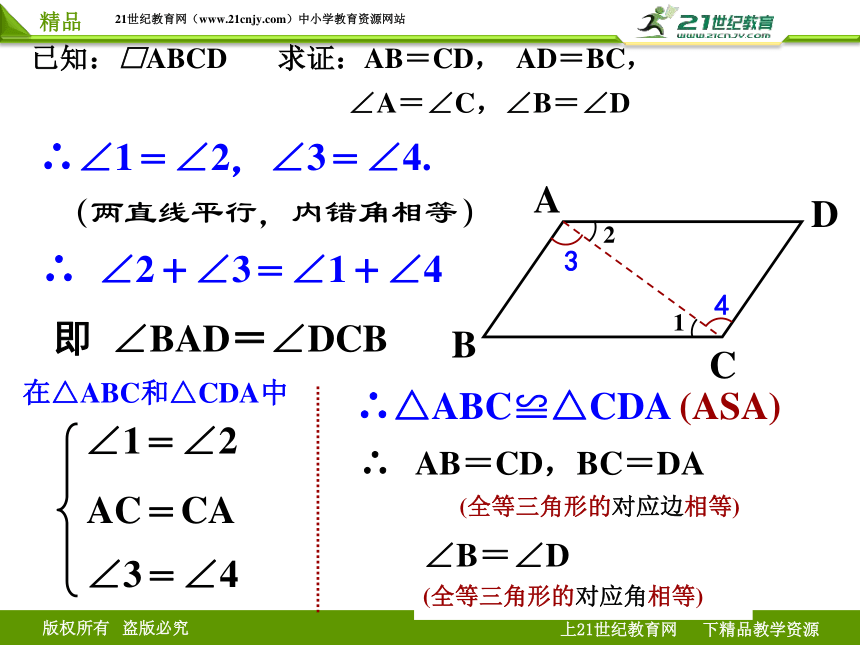
已知:□ABCD 求证:AB=CD, AD=BC,
∠A=∠C,∠B=∠D
A
B
C
D
2
1
4
3
∴∠1=∠2,∠3=∠4.
(两直线平行,内错角相等)
∴ ∠2+∠3=∠1+∠4
即 ∠BAD=∠DCB
在△ABC和△CDA中
∠1=∠2
AC=CA
∠3=∠4
∴△ABC≌△CDA (ASA)
∴ AB=CD,BC=DA
(全等三角形的对应边相等)
∠B=∠D
(全等三角形的对应角相等)
′
四、平行四边形的性质
Ⅱ、平行四边形的对边相等。
Ⅲ、平行四边形的对角相等。
Ⅰ、平行四边形的对边平行。
〖例1〗如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中AB边长为8m,其他三条边的长各是多少?
A
B
C
D
〖例2〗如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中AB边长为8m,其他三条边的长各是多少?
A
B
C
D
解:∵□ABCD
∴ AB=CD,AD=BC
∵ AB=8m
∴ CD=8m
∵ AB+ BC+CD+AD=36m
∴ AD=BC=10m
证明型的计算题,写出推理的步骤是非常必要的。
1、□ABCD中,AB=5,BC=3,
求它的周长。
解:∵□ABCD
A
D
C
B
∴ AB=CD,AD=BC
∵ AB=5, BC=3
∴ CD=5, AD=3
∴ AB+BC+CD+AD=16
(平行四边形的对边相等)
2、一个平行四边形的一个外角是38°这个平行四边形的每个内角的度数分别是多少?为什么?
解:∵ □ABCD
∴ AD∥BC
A
D
C
B
38°
E
∴ ∠D=∠BCE=38°
∴ ∠B=∠D=38°
3、如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形。线段AD和BC的长度有什么关系?
A
B
C
D
解: ∵AD∥BC (已知)
AB∥DC (已知)
∴ 四边形ABCD是平行四边形。
∴ AD=BC
(平行四边形的对边相等)
如图,在纸上画□ABCD,将它剪下,再在一张纸上沿□ABCD的边缘画出一个与□ABCD相同的□EFGH在它们的中心O(两条对角线)的交点钉一个图钉。将□ABCD绕点O旋转180°,它还和□EFGH重合吗?从中你能看出前面得到□ABCD的边、角关系吗?
【操作实验探索新知】
·
A
B
C
D
·
E
F
G
H
O
·
A(E)
B(F)
C(G)
D(H)
O
·
C(E)
D(F)
A(G)
B(H)
O
进一步,你能发现OA与OC,OB与OD的关系吗?
可以发现:
在□ABCD中,OA=OC,OB=OD
·
A
O
B
C
D
由此我们得到了平行四边形的又一个性质:
平行四边形的对角线互相平分.
相信你可以通过三角形全等来证明这个结论.
已知:在□ABCD中,对角线AC和BD相交于点O。求证:OA=OC,OB=OD
·
A
O
B
C
D
平行四边形的对角线互相平分.
证明:∵ □ABCD
2
1
4
3
∴AD=BC
AD∥BC
∴ ∠1=∠2
∠3=∠4
在△AOD和△COB中
已知:在□ABCD中,对角线AC和BD相交于点O。求证:OA=OC,OB=OD
平行四边形的对角线互相平分.
·
A
O
B
C
D
2
1
4
3
在△AOD和△COB中
∠1=∠2
AD=CB
∠3=∠4
∴△AOD≌△COB (ASA)
∴ OA=OC,OD=OB (全等三角形的对应边相等)
〖例2〗如图,在□ABCD中,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长以及□ABCD的面积。
A
B
C
D
O
证明:∵ □ABCD
∴BC=AD=8
CD=AB=10
∵AC⊥BC
∴△ABC是直角三角形。
〖例2〗如图,在□ABCD中,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长以及□ABCD的面积。
A
B
C
D
O
∴△ABC是直角三角形。
AC=
=6
又∵ OA=OC
=3
S□ABCD=BC·AC
=8×6
=48
1、如图,在□ABCD中,BC=10cm,AC=8cm,BD=14cm,△AOD的周长是多少?为什么? △ABC与△DBC 的周长哪个长?长多少?
A
B
C
D
O
解: ⑴∵ □ABCD
∴AD=BC=10cm
=4cm
=7cm
1、如图,在□ABCD中,BC=10cm,AC=8cm,BD=14cm,△AOD的周长是多少?为什么? △ABC与△DBC 的周长哪个长?长多少?
A
B
C
D
O
解: ⑴∵ □ABCD
∴ AD=BC=10cm
=4cm
=7cm
∴ OA+OD+AD
=4+7+10
=21(cm)
1、如图,在□ABCD中,BC=10cm,AC=8cm,BD=14cm,△AOD的周长是多少?为什么? △ABC与△DBC 的周长哪个长?长多少?
A
B
C
D
O
⑵ △DBC的周长-△ABC的周长
=(BD+BC+CD)
-(AB+BC+AC)
=(14+10+CD)
-(AB+10+8)
=24-18
=6 (cm)
答:△ABC的周长比△DBC 的周长长6cm。
2、如图,□ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F。求证:OE=OF
A
B
C
D
O
E
F
证明:∵ □ABCD
∴OB=OD,AB∥CD
2
1
4
3
∴ ∠1=∠2
在△BOE和△DOF中
2、如图,□ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F。求证:OE=OF
OB=OD
A
B
C
D
O
E
F
2
1
4
3
∠1=∠2
在△BOE和△DOF中
∠3=∠4
∴△BOE≌△DOF (ASA)
∴ OE=OF (全等三角形的对应边相等)
B
D
C
A
平行四边形的性质
小结
定理一: 平行四边形的对边平行.
叙述为:
∵ 四边形ABCD是平行四边形.
∴ AB∥CD,AD∥BC
B
D
C
A
平行四边形的性质
小结
定理二: 平行四边形的对边相等.
叙述为:
∵ 四边形ABCD是平行四边形.
∴ AB=CD,BC=AD
B
D
C
A
平行四边形的性质
小结
定理三: 平行四边形的对角相等.
叙述为:
∵ 四边形ABCD是平行四边形.
∴ ∠A=∠C,∠B=∠D
B
D
C
A
平行四边形的性质
小结
定理四: 平行四边形的对角线互相平分.
叙述为:
∵ 四边形ABCD是平行四边形.
∴ OA=OC,OB=OD
O
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
平行四边形的
定义和性质
人教版 八年级下
一、引言
现实世界中,四边形也在装点着我们的生活。宏伟的建筑物、铺满地砖的地板、别具一格的窗棂、天空飞舞的风筝······处处都有四边形的身影。
一、引言
在小学,我们已经学过一些特殊的四边形,如长方形、正方形、平行四边形和梯形等,这些特殊的四边形与我们的生活关系更为密切。
在本章,我们将进一步认识这些特殊的四边形,分析它们的联系与区别,探索并证明它们的性质及判定方法,进一步提高分析问题、解决问题的能力。
一、引言
二、生活中的四边形
平行四边形是我们常见的图形,小区的伸缩门、庭院的竹篱笆、载重汽车的防护栏,都是平行四边形的形象。
三、平行四边形的定义
我们已经知道:
1、定义:有两组对边分别平行的
四边形叫做平行四边形。
2、表示:平行四边形用“ □ ”表示
3、写法:平行四边形ABCD记作□ ABCD
A
B
C
D
四、平行四边形的性质
由平行四边形的定义,我们知道:
平行四边形的两组对边分别平行。
除此之外,平行四边形还有什么性质呢?
也就是说,它的边、角有什么关系?
量一量,你一定能猜想到的。试试看:
′
四、平行四边形的性质
1、平行四边形的两组对边分别平行。
2、平行四边形的对边相等。
3、平行四边形的对角相等。
我们知道,真命题必须经过证明,才能承认它的正确性。
平行四边形的对边相等.
已知:□ABCD
求证:AB=CD, AD=BC,
∠A=∠C,∠B=∠D
A
B
C
D
证明:连接AC.
平行四边形的对角相等.
∵□ABCD(已知)
∴AB∥CD,AD∥BC
(平行四边形的两组对边分别平行。)
已知:□ABCD 求证:AB=CD, AD=BC,
∠A=∠C,∠B=∠D
A
B
C
D
2
1
4
3
∴∠1=∠2,∠3=∠4.
(两直线平行,内错角相等)
∴ ∠2+∠3=∠1+∠4
即 ∠BAD=∠DCB
在△ABC和△CDA中
∠1=∠2
AC=CA
∠3=∠4
∴△ABC≌△CDA (ASA)
∴ AB=CD,BC=DA
(全等三角形的对应边相等)
∠B=∠D
(全等三角形的对应角相等)
′
四、平行四边形的性质
Ⅱ、平行四边形的对边相等。
Ⅲ、平行四边形的对角相等。
Ⅰ、平行四边形的对边平行。
〖例1〗如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中AB边长为8m,其他三条边的长各是多少?
A
B
C
D
〖例2〗如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中AB边长为8m,其他三条边的长各是多少?
A
B
C
D
解:∵□ABCD
∴ AB=CD,AD=BC
∵ AB=8m
∴ CD=8m
∵ AB+ BC+CD+AD=36m
∴ AD=BC=10m
证明型的计算题,写出推理的步骤是非常必要的。
1、□ABCD中,AB=5,BC=3,
求它的周长。
解:∵□ABCD
A
D
C
B
∴ AB=CD,AD=BC
∵ AB=5, BC=3
∴ CD=5, AD=3
∴ AB+BC+CD+AD=16
(平行四边形的对边相等)
2、一个平行四边形的一个外角是38°这个平行四边形的每个内角的度数分别是多少?为什么?
解:∵ □ABCD
∴ AD∥BC
A
D
C
B
38°
E
∴ ∠D=∠BCE=38°
∴ ∠B=∠D=38°
3、如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形。线段AD和BC的长度有什么关系?
A
B
C
D
解: ∵AD∥BC (已知)
AB∥DC (已知)
∴ 四边形ABCD是平行四边形。
∴ AD=BC
(平行四边形的对边相等)
如图,在纸上画□ABCD,将它剪下,再在一张纸上沿□ABCD的边缘画出一个与□ABCD相同的□EFGH在它们的中心O(两条对角线)的交点钉一个图钉。将□ABCD绕点O旋转180°,它还和□EFGH重合吗?从中你能看出前面得到□ABCD的边、角关系吗?
【操作实验探索新知】
·
A
B
C
D
·
E
F
G
H
O
·
A(E)
B(F)
C(G)
D(H)
O
·
C(E)
D(F)
A(G)
B(H)
O
进一步,你能发现OA与OC,OB与OD的关系吗?
可以发现:
在□ABCD中,OA=OC,OB=OD
·
A
O
B
C
D
由此我们得到了平行四边形的又一个性质:
平行四边形的对角线互相平分.
相信你可以通过三角形全等来证明这个结论.
已知:在□ABCD中,对角线AC和BD相交于点O。求证:OA=OC,OB=OD
·
A
O
B
C
D
平行四边形的对角线互相平分.
证明:∵ □ABCD
2
1
4
3
∴AD=BC
AD∥BC
∴ ∠1=∠2
∠3=∠4
在△AOD和△COB中
已知:在□ABCD中,对角线AC和BD相交于点O。求证:OA=OC,OB=OD
平行四边形的对角线互相平分.
·
A
O
B
C
D
2
1
4
3
在△AOD和△COB中
∠1=∠2
AD=CB
∠3=∠4
∴△AOD≌△COB (ASA)
∴ OA=OC,OD=OB (全等三角形的对应边相等)
〖例2〗如图,在□ABCD中,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长以及□ABCD的面积。
A
B
C
D
O
证明:∵ □ABCD
∴BC=AD=8
CD=AB=10
∵AC⊥BC
∴△ABC是直角三角形。
〖例2〗如图,在□ABCD中,AB=10,AD=8,AC⊥BC,求BC,CD,AC,OA的长以及□ABCD的面积。
A
B
C
D
O
∴△ABC是直角三角形。
AC=
=6
又∵ OA=OC
=3
S□ABCD=BC·AC
=8×6
=48
1、如图,在□ABCD中,BC=10cm,AC=8cm,BD=14cm,△AOD的周长是多少?为什么? △ABC与△DBC 的周长哪个长?长多少?
A
B
C
D
O
解: ⑴∵ □ABCD
∴AD=BC=10cm
=4cm
=7cm
1、如图,在□ABCD中,BC=10cm,AC=8cm,BD=14cm,△AOD的周长是多少?为什么? △ABC与△DBC 的周长哪个长?长多少?
A
B
C
D
O
解: ⑴∵ □ABCD
∴ AD=BC=10cm
=4cm
=7cm
∴ OA+OD+AD
=4+7+10
=21(cm)
1、如图,在□ABCD中,BC=10cm,AC=8cm,BD=14cm,△AOD的周长是多少?为什么? △ABC与△DBC 的周长哪个长?长多少?
A
B
C
D
O
⑵ △DBC的周长-△ABC的周长
=(BD+BC+CD)
-(AB+BC+AC)
=(14+10+CD)
-(AB+10+8)
=24-18
=6 (cm)
答:△ABC的周长比△DBC 的周长长6cm。
2、如图,□ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F。求证:OE=OF
A
B
C
D
O
E
F
证明:∵ □ABCD
∴OB=OD,AB∥CD
2
1
4
3
∴ ∠1=∠2
在△BOE和△DOF中
2、如图,□ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F。求证:OE=OF
OB=OD
A
B
C
D
O
E
F
2
1
4
3
∠1=∠2
在△BOE和△DOF中
∠3=∠4
∴△BOE≌△DOF (ASA)
∴ OE=OF (全等三角形的对应边相等)
B
D
C
A
平行四边形的性质
小结
定理一: 平行四边形的对边平行.
叙述为:
∵ 四边形ABCD是平行四边形.
∴ AB∥CD,AD∥BC
B
D
C
A
平行四边形的性质
小结
定理二: 平行四边形的对边相等.
叙述为:
∵ 四边形ABCD是平行四边形.
∴ AB=CD,BC=AD
B
D
C
A
平行四边形的性质
小结
定理三: 平行四边形的对角相等.
叙述为:
∵ 四边形ABCD是平行四边形.
∴ ∠A=∠C,∠B=∠D
B
D
C
A
平行四边形的性质
小结
定理四: 平行四边形的对角线互相平分.
叙述为:
∵ 四边形ABCD是平行四边形.
∴ OA=OC,OB=OD
O
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
