18.1.2平行四边形的判定(课件)
图片预览


文档简介
(共40张PPT)
平行四边形的判定
人教版 八年级下
平行四边形的对边相等;
平行四边形的对角相等;
平行四边形的对角线互相平分。
通过前面的学习,我们知道:
〖思考〗
反过来:
对边相等的四边形是平行四边形;
对角相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形。
正确吗?
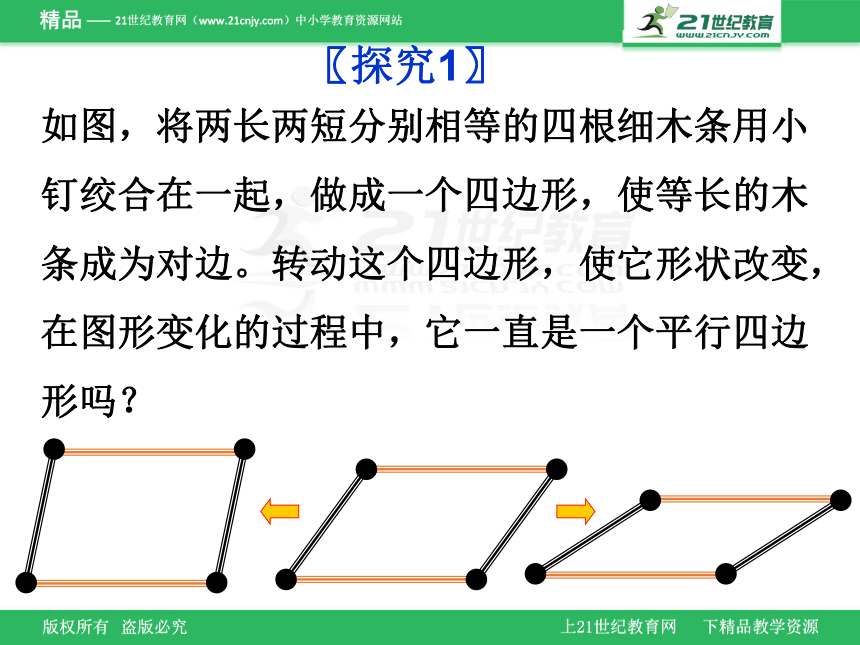
〖探究1〗
如图,将两长两短分别相等的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边。转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?
A
B
C
D
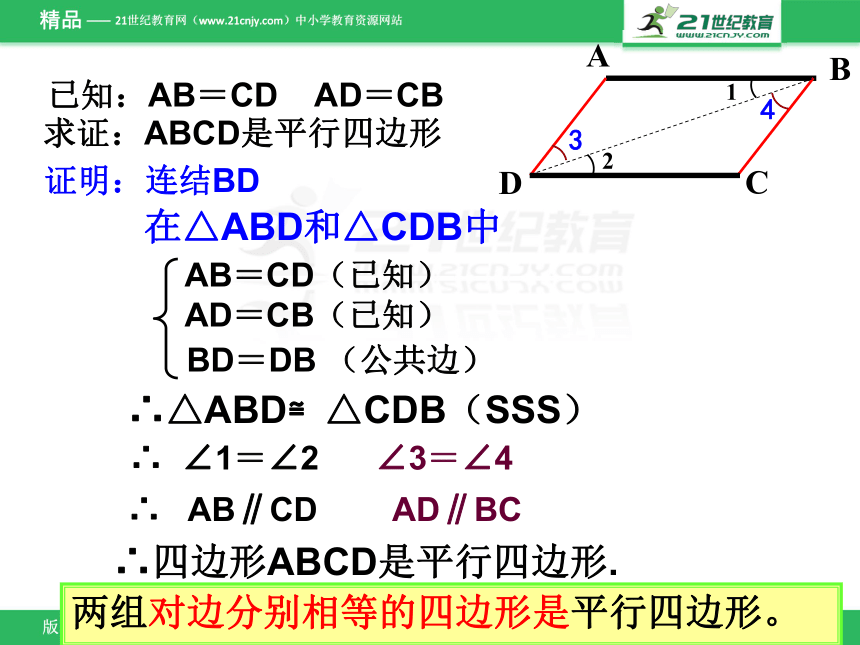
证明:连结BD
∴四边形ABCD是平行四边形.
求证:ABCD是平行四边形
已知:AB=CD AD=CB
AB=CD(已知)
∴ AB∥CD AD∥BC
∴ ∠1=∠2 ∠3=∠4
∴△ABD≌△CDB(SSS)
在△ABD和△CDB中
AD=CB(已知)
BD=DB (公共边)
2
1
3
4
两组对边分别相等的四边形是平行四边形。
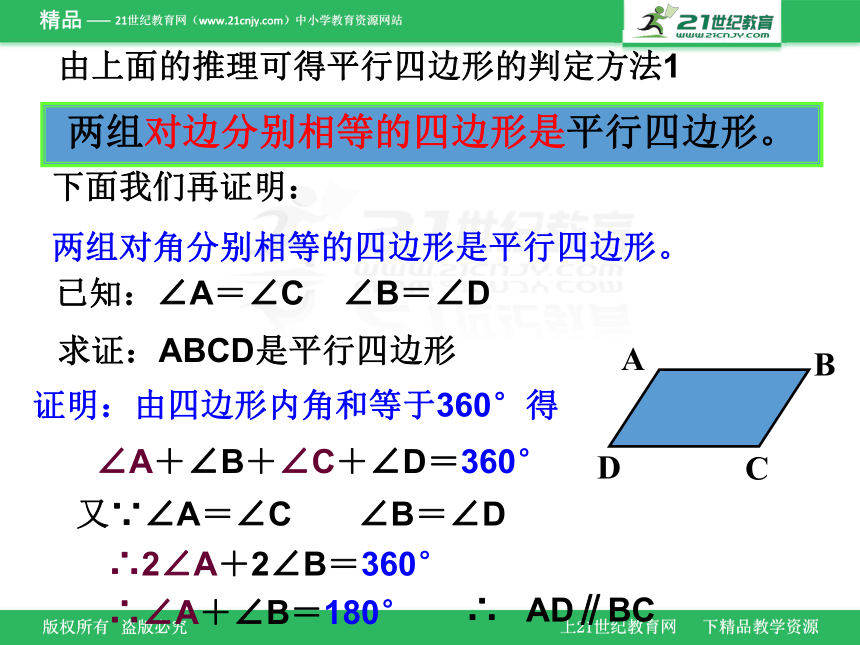
证明:由四边形内角和等于360°得
由上面的推理可得平行四边形的判定方法1
求证:ABCD是平行四边形
已知:∠A=∠C ∠B=∠D
又∵∠A=∠C ∠B=∠D
∠A+∠B+∠C+∠D=360°
两组对边分别相等的四边形是平行四边形。
下面我们再证明:
两组对角分别相等的四边形是平行四边形。
A
B
C
D
∴2∠A+2∠B=360°
∴∠A+∠B=180°
∴ AD∥BC
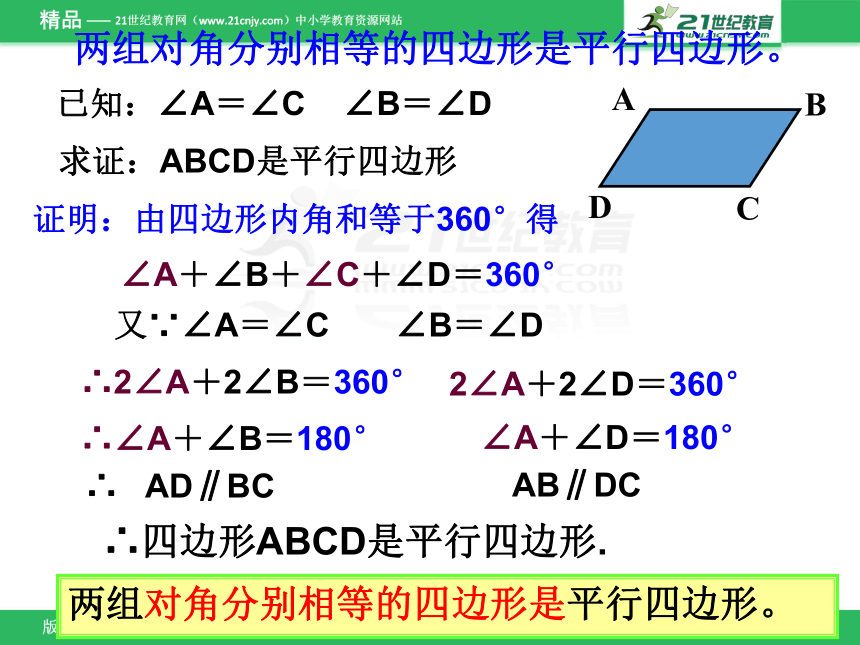
证明:由四边形内角和等于360°得
求证:ABCD是平行四边形
已知:∠A=∠C ∠B=∠D
又∵∠A=∠C ∠B=∠D
∠A+∠B+∠C+∠D=360°
两组对角分别相等的四边形是平行四边形。
A
B
C
D
∴2∠A+2∠B=360°
∴∠A+∠B=180°
∴ AD∥BC
2∠A+2∠D=360°
∠A+∠D=180°
AB∥DC
∴四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形。
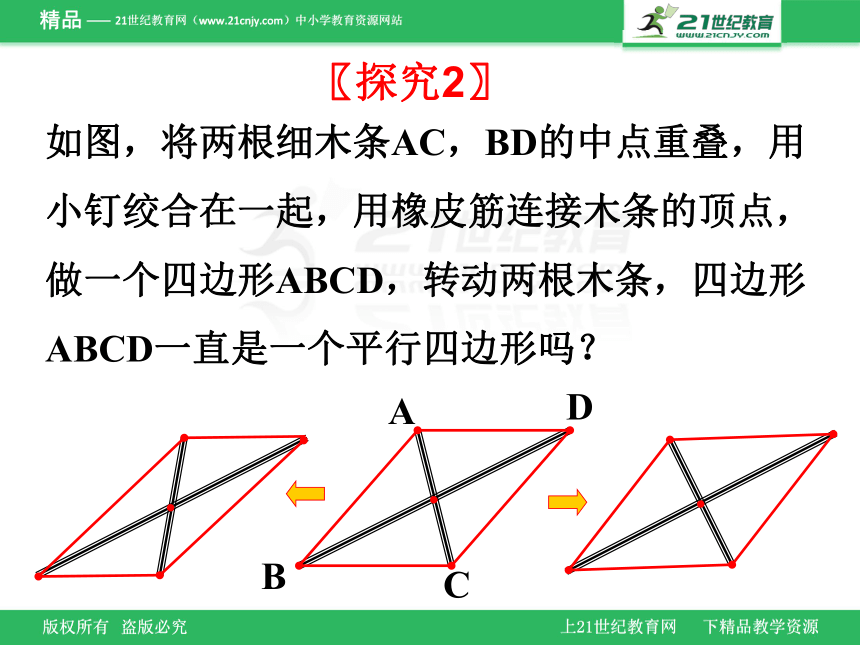
〖探究2〗
如图,将两根细木条AC,BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做一个四边形ABCD,转动两根木条,四边形ABCD一直是一个平行四边形吗?
●
●
●
A
B
C
D
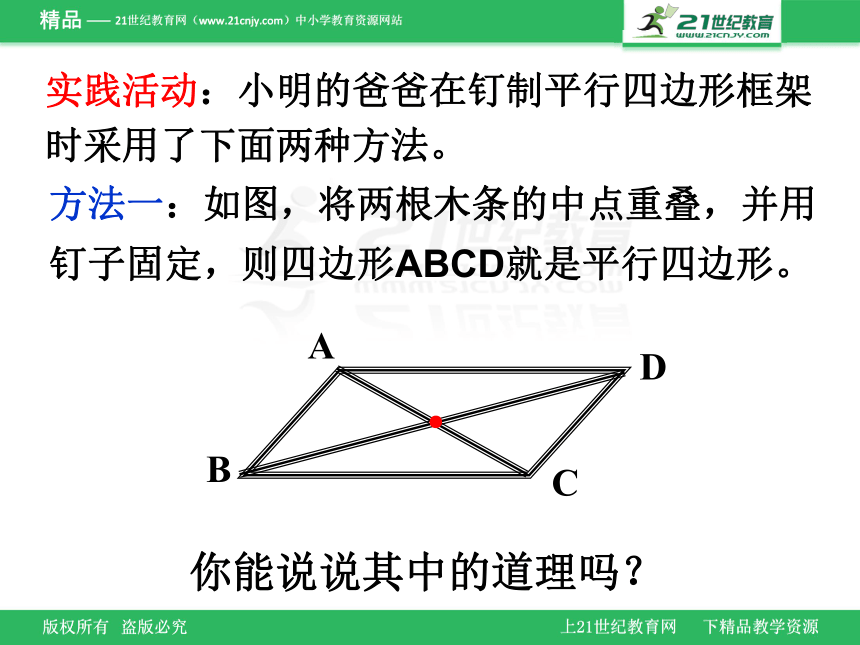
实践活动:小明的爸爸在钉制平行四边形框架时采用了下面两种方法。
A
B
C
D
方法一:如图,将两根木条的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形。
●
你能说说其中的道理吗?
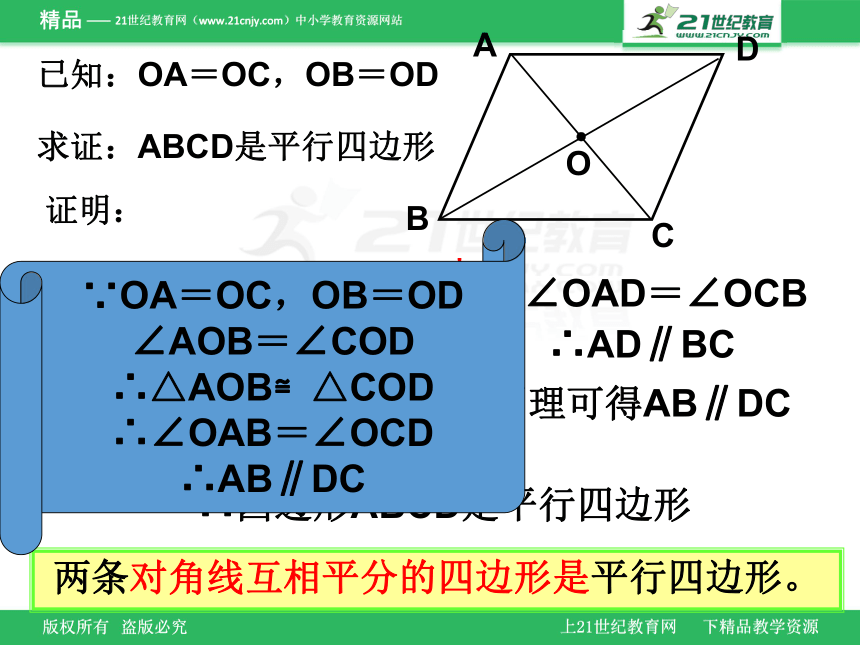
两条对角线互相平分的四边形是平行四边形。
O
A
B
C
D
●
∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
∠AOD=∠COB
∴△AOD≌△COB
∴∠OAD=∠OCB
∴AD∥BC
同理可得AB∥DC
已知:OA=OC,OB=OD
求证:ABCD是平行四边形
证明:
∵OA=OC,OB=OD
∠AOB=∠COD
∴△AOB≌△COD
∴∠OAB=∠OCD
∴AB∥DC
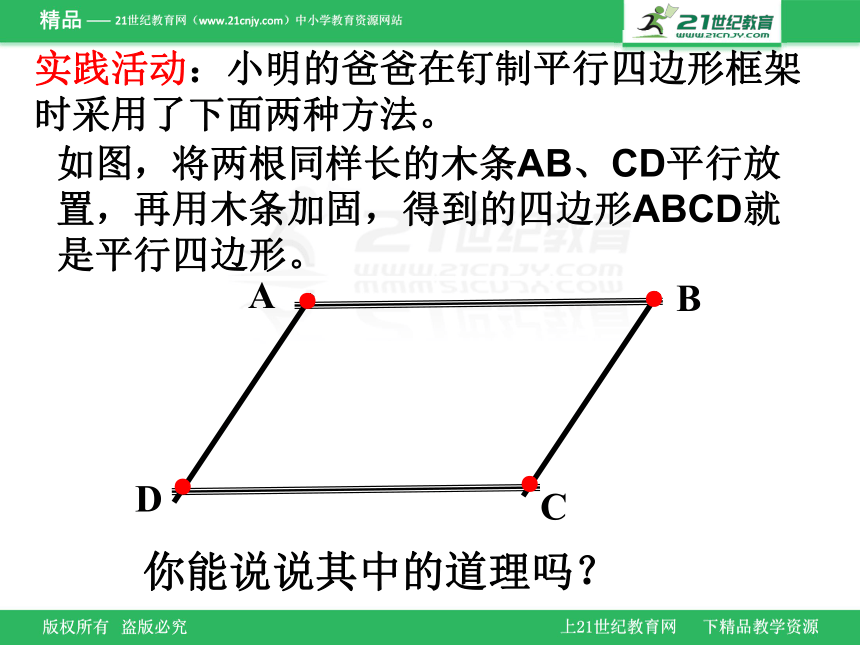
实践活动:小明的爸爸在钉制平行四边形框架时采用了下面两种方法。
A
B
C
D
如图,将两根同样长的木条AB、CD平行放置,再用木条加固,得到的四边形ABCD就是平行四边形。
●
●
●
●
你能说说其中的道理吗?
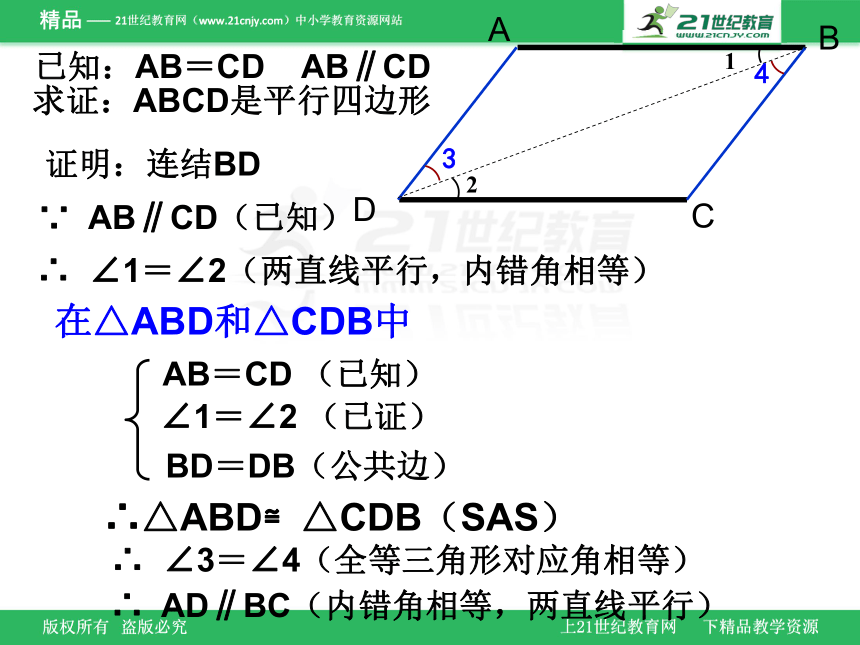
A
B
C
D
证明:连结BD
求证:ABCD是平行四边形
已知:AB=CD AB∥CD
AB=CD (已知)
∵ AB∥CD(已知)
∴ ∠1=∠2(两直线平行,内错角相等)
∴△ABD≌△CDB(SAS)
∴ ∠3=∠4(全等三角形对应角相等)
∴ AD∥BC(内错角相等,两直线平行)
2
1
3
4
在△ABD和△CDB中
∠1=∠2 (已证)
BD=DB(公共边)
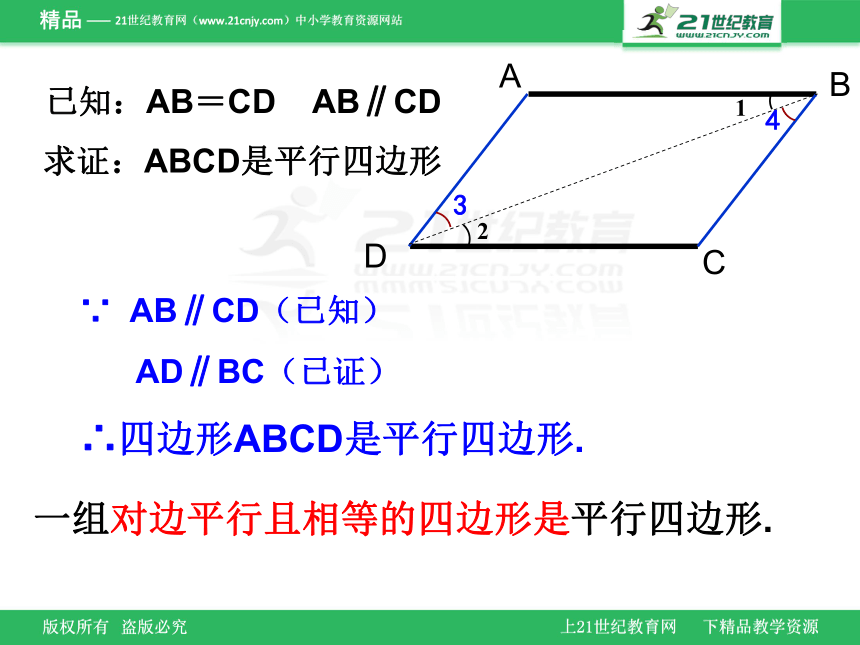
一组对边平行且相等的四边形是平行四边形.
∴四边形ABCD是平行四边形.
求证:ABCD是平行四边形
已知:AB=CD AB∥CD
∵ AB∥CD(已知)
AD∥BC(已证)
A
B
C
D
2
1
3
4
③ 两条对角线互相平分的四边形
是平行四边形。
② 两组对边分别相等的四边形
是平行四边形。
④ 一组对边平行且相等的四边形
是平行四边形。
① 两组对边分别平行的四边形
是平行四边形。
例1、如图,AC∥ED,点B在AC上且AB=ED=BC,找出图中的平行四边形。
A
B
C
D
E
解:□ ABDE,□ BCDE
① ∵ AB∥ED
AB=ED
∴ 四边形ABDE是平行四边形。
例1、如图,AC∥ED,点B在AC上,且AB=ED=BC,找出图中的平行四边形。
A
B
C
D
E
② ∵ BC∥ED BC=ED
∴ 四边形BCDE是平行四边形。
例2、如图,□ABCD中,AC、BD相交于点O,点E、F在对角线AC上,且OE=OF。
①OA与OC,OB与OD是否相等?
②四边形BFDE是平行四边形吗?
A
B
C
D
O
F
E
解:① ∵ □ABCD
∴ OA=OC
OB=OD
(平行四边形的对角线相等)
②四边形BFDE是平行四边形吗?
答:②四边形BFDE是平行四
边形,理由如下 :
∵ □ABCD
又∵ OE=OF
∴ 四边形BFDE是平行四边形。
(对角线互相平分的四边形是平行四边形)
例2、如图,□ABCD中,AC、BD相交于点O,点E、F在对角线AC上,且OE=OF。
A
B
C
D
O
F
E
∴ OB=OD
例3、在□ABCD中,点E、F分别在 AB、CD上,DF=BE,四边形DEBF是平行四边形吗?说说你的理由。
A
B
C
D
F
E
例3、在□ABCD中,点E、F分别在 AB、CD上,DF=BE,四边形DEBF是平行四边形吗?说说你的理由。
A
B
C
D
F
E
∴ DC∥AB
答:四边形DEBF是平行四边形
理由如下:
∵ □ABCD
即DF∥EB
∵DF=EB
∴四边形DEBF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
例4、如图,点D,E分别是△ABC的边
AB、AC的中点,
求证:DE∥BC,且
A
B
C
D
E
证明:延长DE到点F,使
EF=DE
F
连接FC,DC,AF
∵AE=EC
∴ 四边形ADCF是平行四边形。
例4、如图,点D,E分别是△ABC的边AB、AC的中点,
求证:DE∥BC,且
A
B
C
D
E
F
∴ 四边形ADCF是平行四边形。
CF=DA,CF∥DA
∴ CF=BD,CF∥BD
∴ 四边形BDFC是平行四边形。
∴ DF=BC,DF∥BC
∴ DE∥BC
连接三角形两边中点的线段
叫做三角形的中位线。
三角形的中位线
A
B
C
D
E
A
B
C
F
E
DE、EF是△ABC的中位线。
三角形的中位线定理
A
B
C
D
E
三角形的中位线平行于三角形的第三边,
且等于第三边的一半。
⑴ ∵ DE是△ABC的中位线,
∴ DE∥BC
三角形的中位线定理
A
B
C
D
E
三角形的中位线平行于三角形的第三边,
且等于第三边的一半。
⑵∵ AD=BD,AE=CE
∴ DE∥BC
以上两种方式都是三角形的中位线定理的推理过程。
求证:夹在两条平行线间的平行线段相等。
已知:如图,直线 m∥n,线段AB、CD分别交m、n于点A、B和D、C,且有AB∥CD
求证:AB=CD
m
n
A
D
C
B
证明:∵ m∥n
又 AB∥CD
即 AD∥BC
∴ 四边形ABCD是平行四边形。
∴ AB=CD
两条平行线间的距离
a
b
A
D
C
B
已知:直线a∥b,从直线a上的任意一点A向直线b作垂线段AB,垂足为B,按同样的方法,作出线段CD。
由 “夹在两条平行线间的平行线段相等”
得 AB=CD
AB、CD 是这两条平行线间最短的线段,
我们把这种线段的长度叫做两条平行线间的距离。
两条平行线间的距离
a
b
A
B
从两条平行线中的一条直线上的任意一点,向另一条直线作垂线段,这条垂线段的长度叫做两条平行线间的距离。
线段AB、CD的长度都是a、b之间的距离。
C
D
1、如图, AB=DC=EF, AD=BC,DE=CF,图中有哪些互相平行的线段?
A
B
D
C
F
E
解:AB∥DC∥EF
AD∥BC
DE∥CF
2、如图,□ABCD中, O 是AC、BD的交点,点E、F、G、H分别是AO、BO、CO、DO的中点。四边形EFGH是平行四边形吗?说说你的理由
A
B
C
D
O
F
E
G
H
A
B
C
D
O
F
E
G
H
解:四边形EFGH是平行四边形,理由如下:
∵ □ABCD
∴ OA=OC, OB=OD
∵ E、F、G、H分别是AO、BO、CO、DO的中点。
∴ OE=OG, OF=OH
∴四边形EFGH是平行四边形。
2、如图,□ABCD中, O 是AC、BD的交点,点E、F、G、H分别是AO、BO、CO、DO的中点。四边形EFGH是平行四边形吗?说说你的理由
3、如图,点D,E,F分别是△ABC的边AB,BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?
A
B
C
D
F
E
●
●
●
□ ADEF
□ BDFE
□ CEDF
4、如图,在□ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN。 EM和FN有什么关系?为什么?
A
B
C
D
F
E
M
N
解: EM∥FN ,EM=FN 理由如下:
∵ EF=MN, EF∥MN
∴ 四边形EMNF是平行四边形
∴ EM∥FN
EM=FN
5、如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点间的实际距离?根据是什么?
A
B
C
E
F
解: 分别取AC、BC的中点E、F
连接EF,量得EF的长
则AB=2EF
根据三角形的中位线等于第三边的一半。
⑴ 一组对边平行另一组对边相等的四边形
是平行四边形吗?
议一议,做一做
答:不一定是平行四边形,可能是
平行四边形或等腰梯形。
A
B
C
D
A
B
C
D
AB∥CD,AD=BC
⑵ 一组对边平行一组对角相等的四边形
是平行四边形吗?
议一议,做一做
答:是平行四边形,理由如下:
A
B
C
D
证明:连接BD
求证:四边形ABCD是平行四边形。
已知:AB∥CD,∠A=∠C
∵ AB∥CD
∴∠ABD=∠CDB
议一议,做一做
证明:连接BD
∵ AB∥CD
∴∠ABD=∠CDB
A
B
C
D
∠A=∠C (已知)
∴△ABD≌△CDB(ASA)
∴ AB=CD(全等三角形对应边相等)
在△ABD和△CDB中
AB=CD (已知)
∠ABD=∠CDB(已证)
∴ 四边形ABCD是平行四边形。
⑶ 一组对角相等一组对边相等的四边形
是平行四边形吗?
议一议,做一做
答:不是平行四边形,举例如下:
A
B
C
D
E
∠D=∠E,AE=DC
四边形ADCE不是平行四边形。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
平行四边形的判定
人教版 八年级下
平行四边形的对边相等;
平行四边形的对角相等;
平行四边形的对角线互相平分。
通过前面的学习,我们知道:
〖思考〗
反过来:
对边相等的四边形是平行四边形;
对角相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形。
正确吗?
〖探究1〗
如图,将两长两短分别相等的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边。转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?
A
B
C
D
证明:连结BD
∴四边形ABCD是平行四边形.
求证:ABCD是平行四边形
已知:AB=CD AD=CB
AB=CD(已知)
∴ AB∥CD AD∥BC
∴ ∠1=∠2 ∠3=∠4
∴△ABD≌△CDB(SSS)
在△ABD和△CDB中
AD=CB(已知)
BD=DB (公共边)
2
1
3
4
两组对边分别相等的四边形是平行四边形。
证明:由四边形内角和等于360°得
由上面的推理可得平行四边形的判定方法1
求证:ABCD是平行四边形
已知:∠A=∠C ∠B=∠D
又∵∠A=∠C ∠B=∠D
∠A+∠B+∠C+∠D=360°
两组对边分别相等的四边形是平行四边形。
下面我们再证明:
两组对角分别相等的四边形是平行四边形。
A
B
C
D
∴2∠A+2∠B=360°
∴∠A+∠B=180°
∴ AD∥BC
证明:由四边形内角和等于360°得
求证:ABCD是平行四边形
已知:∠A=∠C ∠B=∠D
又∵∠A=∠C ∠B=∠D
∠A+∠B+∠C+∠D=360°
两组对角分别相等的四边形是平行四边形。
A
B
C
D
∴2∠A+2∠B=360°
∴∠A+∠B=180°
∴ AD∥BC
2∠A+2∠D=360°
∠A+∠D=180°
AB∥DC
∴四边形ABCD是平行四边形.
两组对角分别相等的四边形是平行四边形。
〖探究2〗
如图,将两根细木条AC,BD的中点重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做一个四边形ABCD,转动两根木条,四边形ABCD一直是一个平行四边形吗?
●
●
●
A
B
C
D
实践活动:小明的爸爸在钉制平行四边形框架时采用了下面两种方法。
A
B
C
D
方法一:如图,将两根木条的中点重叠,并用钉子固定,则四边形ABCD就是平行四边形。
●
你能说说其中的道理吗?
两条对角线互相平分的四边形是平行四边形。
O
A
B
C
D
●
∵OA=OC,OB=OD
∴四边形ABCD是平行四边形
∠AOD=∠COB
∴△AOD≌△COB
∴∠OAD=∠OCB
∴AD∥BC
同理可得AB∥DC
已知:OA=OC,OB=OD
求证:ABCD是平行四边形
证明:
∵OA=OC,OB=OD
∠AOB=∠COD
∴△AOB≌△COD
∴∠OAB=∠OCD
∴AB∥DC
实践活动:小明的爸爸在钉制平行四边形框架时采用了下面两种方法。
A
B
C
D
如图,将两根同样长的木条AB、CD平行放置,再用木条加固,得到的四边形ABCD就是平行四边形。
●
●
●
●
你能说说其中的道理吗?
A
B
C
D
证明:连结BD
求证:ABCD是平行四边形
已知:AB=CD AB∥CD
AB=CD (已知)
∵ AB∥CD(已知)
∴ ∠1=∠2(两直线平行,内错角相等)
∴△ABD≌△CDB(SAS)
∴ ∠3=∠4(全等三角形对应角相等)
∴ AD∥BC(内错角相等,两直线平行)
2
1
3
4
在△ABD和△CDB中
∠1=∠2 (已证)
BD=DB(公共边)
一组对边平行且相等的四边形是平行四边形.
∴四边形ABCD是平行四边形.
求证:ABCD是平行四边形
已知:AB=CD AB∥CD
∵ AB∥CD(已知)
AD∥BC(已证)
A
B
C
D
2
1
3
4
③ 两条对角线互相平分的四边形
是平行四边形。
② 两组对边分别相等的四边形
是平行四边形。
④ 一组对边平行且相等的四边形
是平行四边形。
① 两组对边分别平行的四边形
是平行四边形。
例1、如图,AC∥ED,点B在AC上且AB=ED=BC,找出图中的平行四边形。
A
B
C
D
E
解:□ ABDE,□ BCDE
① ∵ AB∥ED
AB=ED
∴ 四边形ABDE是平行四边形。
例1、如图,AC∥ED,点B在AC上,且AB=ED=BC,找出图中的平行四边形。
A
B
C
D
E
② ∵ BC∥ED BC=ED
∴ 四边形BCDE是平行四边形。
例2、如图,□ABCD中,AC、BD相交于点O,点E、F在对角线AC上,且OE=OF。
①OA与OC,OB与OD是否相等?
②四边形BFDE是平行四边形吗?
A
B
C
D
O
F
E
解:① ∵ □ABCD
∴ OA=OC
OB=OD
(平行四边形的对角线相等)
②四边形BFDE是平行四边形吗?
答:②四边形BFDE是平行四
边形,理由如下 :
∵ □ABCD
又∵ OE=OF
∴ 四边形BFDE是平行四边形。
(对角线互相平分的四边形是平行四边形)
例2、如图,□ABCD中,AC、BD相交于点O,点E、F在对角线AC上,且OE=OF。
A
B
C
D
O
F
E
∴ OB=OD
例3、在□ABCD中,点E、F分别在 AB、CD上,DF=BE,四边形DEBF是平行四边形吗?说说你的理由。
A
B
C
D
F
E
例3、在□ABCD中,点E、F分别在 AB、CD上,DF=BE,四边形DEBF是平行四边形吗?说说你的理由。
A
B
C
D
F
E
∴ DC∥AB
答:四边形DEBF是平行四边形
理由如下:
∵ □ABCD
即DF∥EB
∵DF=EB
∴四边形DEBF是平行四边形
(一组对边平行且相等的四边形是平行四边形)
例4、如图,点D,E分别是△ABC的边
AB、AC的中点,
求证:DE∥BC,且
A
B
C
D
E
证明:延长DE到点F,使
EF=DE
F
连接FC,DC,AF
∵AE=EC
∴ 四边形ADCF是平行四边形。
例4、如图,点D,E分别是△ABC的边AB、AC的中点,
求证:DE∥BC,且
A
B
C
D
E
F
∴ 四边形ADCF是平行四边形。
CF=DA,CF∥DA
∴ CF=BD,CF∥BD
∴ 四边形BDFC是平行四边形。
∴ DF=BC,DF∥BC
∴ DE∥BC
连接三角形两边中点的线段
叫做三角形的中位线。
三角形的中位线
A
B
C
D
E
A
B
C
F
E
DE、EF是△ABC的中位线。
三角形的中位线定理
A
B
C
D
E
三角形的中位线平行于三角形的第三边,
且等于第三边的一半。
⑴ ∵ DE是△ABC的中位线,
∴ DE∥BC
三角形的中位线定理
A
B
C
D
E
三角形的中位线平行于三角形的第三边,
且等于第三边的一半。
⑵∵ AD=BD,AE=CE
∴ DE∥BC
以上两种方式都是三角形的中位线定理的推理过程。
求证:夹在两条平行线间的平行线段相等。
已知:如图,直线 m∥n,线段AB、CD分别交m、n于点A、B和D、C,且有AB∥CD
求证:AB=CD
m
n
A
D
C
B
证明:∵ m∥n
又 AB∥CD
即 AD∥BC
∴ 四边形ABCD是平行四边形。
∴ AB=CD
两条平行线间的距离
a
b
A
D
C
B
已知:直线a∥b,从直线a上的任意一点A向直线b作垂线段AB,垂足为B,按同样的方法,作出线段CD。
由 “夹在两条平行线间的平行线段相等”
得 AB=CD
AB、CD 是这两条平行线间最短的线段,
我们把这种线段的长度叫做两条平行线间的距离。
两条平行线间的距离
a
b
A
B
从两条平行线中的一条直线上的任意一点,向另一条直线作垂线段,这条垂线段的长度叫做两条平行线间的距离。
线段AB、CD的长度都是a、b之间的距离。
C
D
1、如图, AB=DC=EF, AD=BC,DE=CF,图中有哪些互相平行的线段?
A
B
D
C
F
E
解:AB∥DC∥EF
AD∥BC
DE∥CF
2、如图,□ABCD中, O 是AC、BD的交点,点E、F、G、H分别是AO、BO、CO、DO的中点。四边形EFGH是平行四边形吗?说说你的理由
A
B
C
D
O
F
E
G
H
A
B
C
D
O
F
E
G
H
解:四边形EFGH是平行四边形,理由如下:
∵ □ABCD
∴ OA=OC, OB=OD
∵ E、F、G、H分别是AO、BO、CO、DO的中点。
∴ OE=OG, OF=OH
∴四边形EFGH是平行四边形。
2、如图,□ABCD中, O 是AC、BD的交点,点E、F、G、H分别是AO、BO、CO、DO的中点。四边形EFGH是平行四边形吗?说说你的理由
3、如图,点D,E,F分别是△ABC的边AB,BC、CA的中点,以这些点为顶点,你能在图中画出多少个平行四边形?
A
B
C
D
F
E
●
●
●
□ ADEF
□ BDFE
□ CEDF
4、如图,在□ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN。 EM和FN有什么关系?为什么?
A
B
C
D
F
E
M
N
解: EM∥FN ,EM=FN 理由如下:
∵ EF=MN, EF∥MN
∴ 四边形EMNF是平行四边形
∴ EM∥FN
EM=FN
5、如图,A,B两点被池塘隔开,在AB外选一点C,连接AC和BC,怎样测出A、B两点间的实际距离?根据是什么?
A
B
C
E
F
解: 分别取AC、BC的中点E、F
连接EF,量得EF的长
则AB=2EF
根据三角形的中位线等于第三边的一半。
⑴ 一组对边平行另一组对边相等的四边形
是平行四边形吗?
议一议,做一做
答:不一定是平行四边形,可能是
平行四边形或等腰梯形。
A
B
C
D
A
B
C
D
AB∥CD,AD=BC
⑵ 一组对边平行一组对角相等的四边形
是平行四边形吗?
议一议,做一做
答:是平行四边形,理由如下:
A
B
C
D
证明:连接BD
求证:四边形ABCD是平行四边形。
已知:AB∥CD,∠A=∠C
∵ AB∥CD
∴∠ABD=∠CDB
议一议,做一做
证明:连接BD
∵ AB∥CD
∴∠ABD=∠CDB
A
B
C
D
∠A=∠C (已知)
∴△ABD≌△CDB(ASA)
∴ AB=CD(全等三角形对应边相等)
在△ABD和△CDB中
AB=CD (已知)
∠ABD=∠CDB(已证)
∴ 四边形ABCD是平行四边形。
⑶ 一组对角相等一组对边相等的四边形
是平行四边形吗?
议一议,做一做
答:不是平行四边形,举例如下:
A
B
C
D
E
∠D=∠E,AE=DC
四边形ADCE不是平行四边形。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
