18.2.1 矩形(课件)
图片预览




文档简介
(共29张PPT)
矩形
人教版 八年级下
有一个角是直角的平行四边形
叫做矩形。矩形就是长方形。
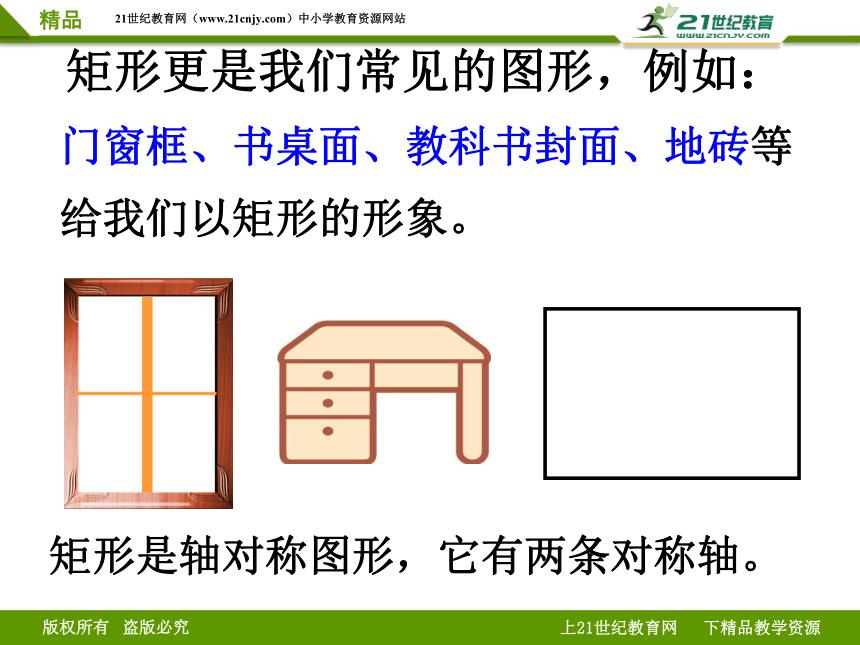
矩形更是我们常见的图形,例如:
门窗框、书桌面、教科书封面、地砖等给我们以矩形的形象。
矩形是轴对称图形,它有两条对称轴。
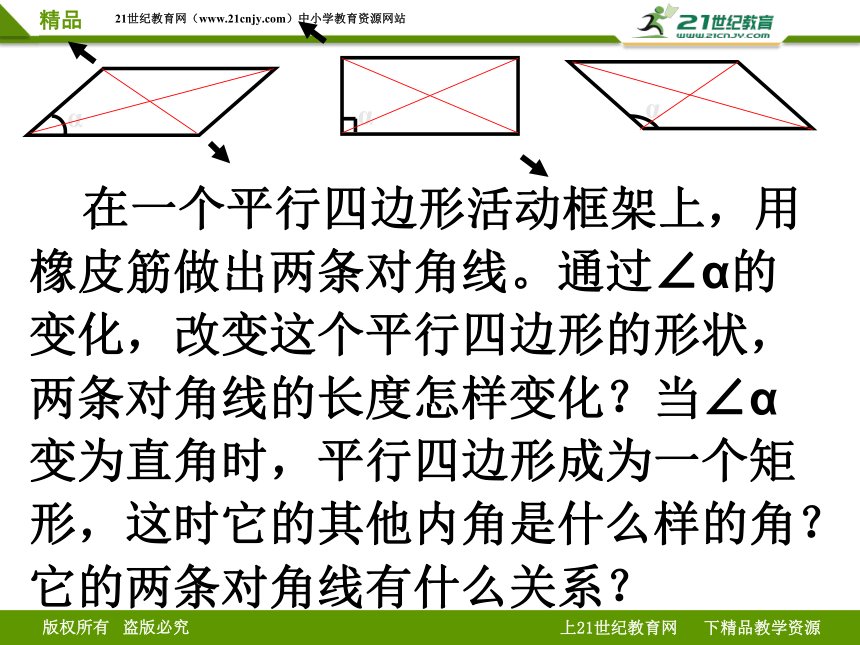
在一个平行四边形活动框架上,用橡皮筋做出两条对角线。通过∠α的变化,改变这个平行四边形的形状,两条对角线的长度怎样变化?当∠α变为直角时,平行四边形成为一个矩形,这时它的其他内角是什么样的角?它的两条对角线有什么关系?
α
α
α
⑴ 随着∠α的变化,两条对角线的长度分别是怎样变化的?
⑵当∠α是锐角时,两条对角线的长度有什么关系?当∠α是钝角时呢?
⑶当∠α是直角时,平行四边形变成矩形,此时,两条对角线的长度有什么关系?
当│∠α-90°│越小两条对角线的差越小。
矩形的对角线相等。
矩形的四个角都是直角;
作为特殊的平行四边形,矩形具有平行四边形的所有性质。
另外,由上面的探究,不难看出,矩形还有以下性质:
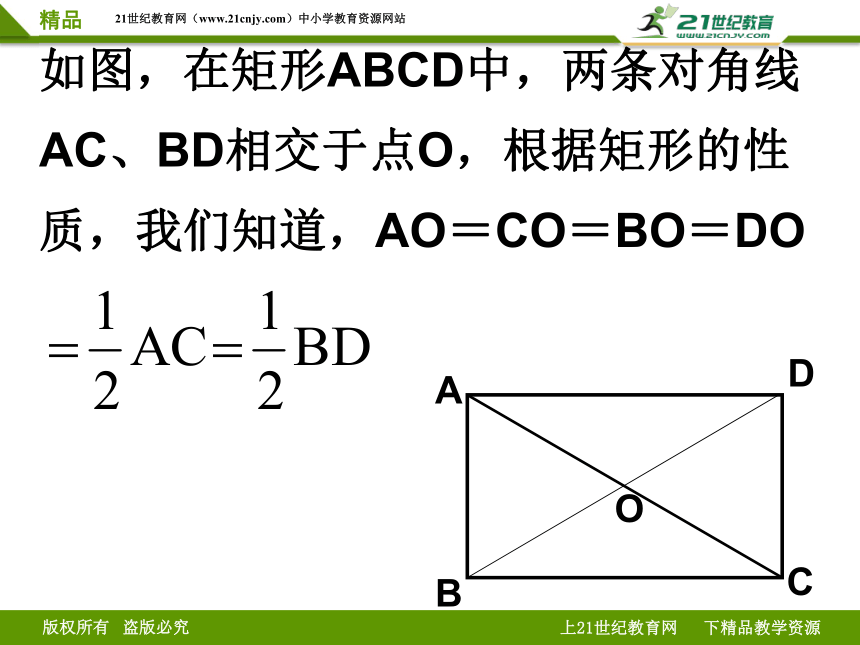
如图,在矩形ABCD中,两条对角线AC、BD相交于点O,根据矩形的性质,我们知道,AO=CO=BO=DO
A
B
C
D
O
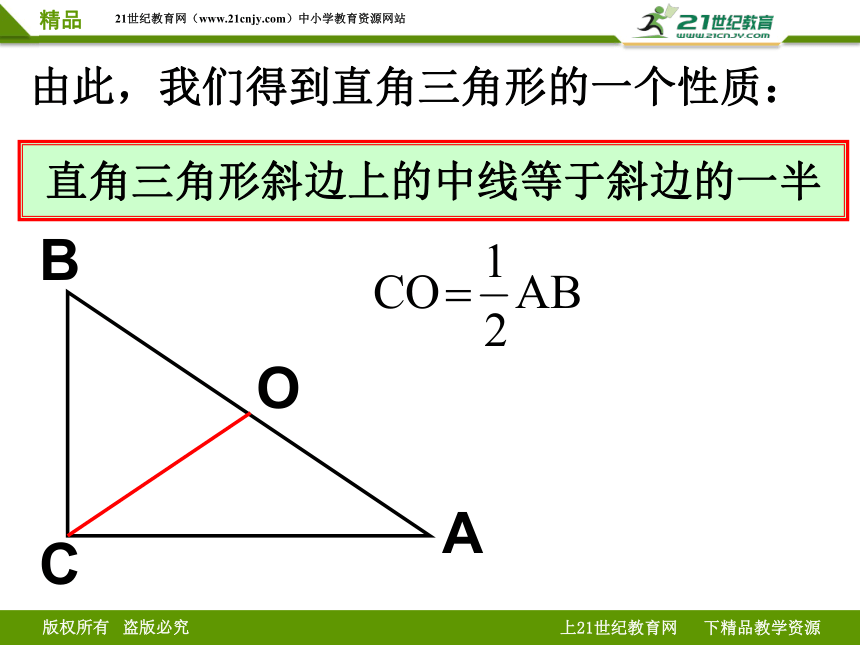
由此,我们得到直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半
A
C
B
O
精典练习题选
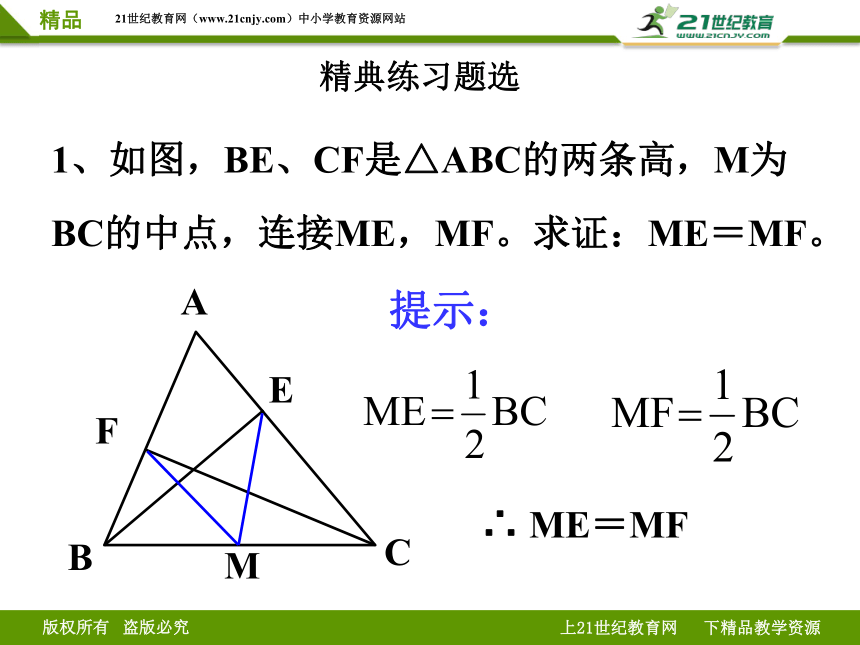
1、如图,BE、CF是△ABC的两条高,M为BC的中点,连接ME,MF。求证:ME=MF。
A
B
C
E
F
M
∴ ME=MF
提示:
精典练习题选
2、如图,以□ABCD的对角线AC为斜边作Rt△AMC,且∠BMD=90°。求证:四边形ABCD是矩形。
A
B
C
O
D
M
∵ BD=2·MO
提示:
AC=2·MO
∴ BD=AC
∴四边形ABCD是矩形。
例1、如图,在矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,求矩形对角线的长。
A
B
C
D
O
例1、如图,在矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,求矩形对角线的长。
A
B
C
D
O
解:∵ 四边形ABCD是矩形。
∴ AC与BD相等且互相平分。
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形。
∴ OA=AB=4cm
∴ 矩形的对角线长AC=BD=2OA=8cm
随堂练习
1、如图,四边形ABCD是矩形,找出相等的线段和相等的角。
A
B
C
D
O
AO=CO=BO=DO
AD=BC,AB=CD
AC=BD
2、求证:矩形的对角线相等。
A
B
C
D
O
已知,四边形ABCD是矩形,
AC、BD是对角线。
求证:AC=BD
2、求证:矩形的对角线相等。
A
B
C
D
O
证明:∵ 四边形ABCD是矩形。
∴AB=DC,∠ABC=∠DCB=90°
在Rt△ABC和Rt△DCB中
AB=DC
∠ABC=∠DCB
BC=CB
∴ Rt△ABC≌Rt△DCB (SAS)
2、求证:矩形的对角线相等。
A
B
C
D
O
在Rt△ABC和Rt△DCB中
AB=DC
∠ABC=∠DCB
BC=CB
∴ Rt△ABC≌Rt△DCB (SAS)
∴AC=BD (全等三角形对应边相等)
3、如果矩形的一条对角线长为8cm,两条对角线的一个交角为120°,求矩形的边长(精确到0.01cm)。
A
B
C
D
O
解:∵∠AOD=120°
∴∠AOB=60°
∵ AO=BO=CO
∴ △AOB是等边三角形。
∴ AB=AO=8÷2=4cm
3、如果矩形的一条对角线长为8cm,两条对角线的一个交角为120°,求矩形的边长(精确到0.01cm)。
A
B
C
D
O
在Rt△ABC中
BC=
答:矩形的边长分别是4cm和
矩形的判定方法
由矩形的定义可知:
有一个角是直角的平行四边形是矩形。
当平行四边形的一角变为直角时,另外三个角同时都变为直角,也使两条对角线成为相等的线段。
矩形的判定方法
由矩形的定义可知:
有一个角是直角的平行四边形是矩形。
矩形的判定定理:
对角线相等的平行四边形是矩形。
矩形的判定定理:
对角线相等的平行四边形是矩形。
已知:□ ABCD,且AC=BD
求证: □ ABCD是矩形。
证明:∵□ ABCD
A
B
C
D
O
∴ AD=BC
AD∥BC
在△ABC和△BAD中
在△ABC和△BAD中
A
B
C
D
O
AB=BA
AC=BD
AD=BC
∴ △ABC≌△BAD (SSS)
∴ ∠ABC=∠BAD
∵ AD∥BC
∴ ∠ABC+∠BAD =180°
A
B
C
D
O
∴ △ABC≌△BAD (SSS)
∴ ∠ABC=∠BAD
∵ AD∥BC
∴ ∠ABC+∠BAD =180°
∴ ∠ABC=∠BAD =90°
∴ 四边形ABCD是矩形。
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形,你知道其中的道理吗?
⑴两组对边相等的四边形是平行四边形;
⑵对角线相等的平行四边形是矩形。
答:量两组对边的长度可知是否为平行四边形;
量两条对角线是否相等可知是否为矩形。
思考
如图,李芳同学用画“边——直角、边——直角、边——直角、边”这样四步画出了一个四边形,她说这就是一个矩形,她的判断对吗?你能证明吗?
边
直角
边
直角
边
直角
边
矩形的判定方法
有三个角是直角的四边形是矩形。
由此,我又得到了矩形的一个判定定理:
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形。
随堂练习
1、八年级⑶班的同学要在广场上布置一个矩形的花坛。计划用“串红”摆成两条对角线。如果一条对角线用了38盆“串红”,还需要从花房运来多少盆“串红”?为什么?如果一条对角线用了49盆呢?为什么?
⑴还要38盆。
⑵还要48盆就够了。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
矩形
人教版 八年级下
有一个角是直角的平行四边形
叫做矩形。矩形就是长方形。
矩形更是我们常见的图形,例如:
门窗框、书桌面、教科书封面、地砖等给我们以矩形的形象。
矩形是轴对称图形,它有两条对称轴。
在一个平行四边形活动框架上,用橡皮筋做出两条对角线。通过∠α的变化,改变这个平行四边形的形状,两条对角线的长度怎样变化?当∠α变为直角时,平行四边形成为一个矩形,这时它的其他内角是什么样的角?它的两条对角线有什么关系?
α
α
α
⑴ 随着∠α的变化,两条对角线的长度分别是怎样变化的?
⑵当∠α是锐角时,两条对角线的长度有什么关系?当∠α是钝角时呢?
⑶当∠α是直角时,平行四边形变成矩形,此时,两条对角线的长度有什么关系?
当│∠α-90°│越小两条对角线的差越小。
矩形的对角线相等。
矩形的四个角都是直角;
作为特殊的平行四边形,矩形具有平行四边形的所有性质。
另外,由上面的探究,不难看出,矩形还有以下性质:
如图,在矩形ABCD中,两条对角线AC、BD相交于点O,根据矩形的性质,我们知道,AO=CO=BO=DO
A
B
C
D
O
由此,我们得到直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半
A
C
B
O
精典练习题选
1、如图,BE、CF是△ABC的两条高,M为BC的中点,连接ME,MF。求证:ME=MF。
A
B
C
E
F
M
∴ ME=MF
提示:
精典练习题选
2、如图,以□ABCD的对角线AC为斜边作Rt△AMC,且∠BMD=90°。求证:四边形ABCD是矩形。
A
B
C
O
D
M
∵ BD=2·MO
提示:
AC=2·MO
∴ BD=AC
∴四边形ABCD是矩形。
例1、如图,在矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,求矩形对角线的长。
A
B
C
D
O
例1、如图,在矩形ABCD的两条对角线相交于O,∠AOB=60°,AB=4cm,求矩形对角线的长。
A
B
C
D
O
解:∵ 四边形ABCD是矩形。
∴ AC与BD相等且互相平分。
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形。
∴ OA=AB=4cm
∴ 矩形的对角线长AC=BD=2OA=8cm
随堂练习
1、如图,四边形ABCD是矩形,找出相等的线段和相等的角。
A
B
C
D
O
AO=CO=BO=DO
AD=BC,AB=CD
AC=BD
2、求证:矩形的对角线相等。
A
B
C
D
O
已知,四边形ABCD是矩形,
AC、BD是对角线。
求证:AC=BD
2、求证:矩形的对角线相等。
A
B
C
D
O
证明:∵ 四边形ABCD是矩形。
∴AB=DC,∠ABC=∠DCB=90°
在Rt△ABC和Rt△DCB中
AB=DC
∠ABC=∠DCB
BC=CB
∴ Rt△ABC≌Rt△DCB (SAS)
2、求证:矩形的对角线相等。
A
B
C
D
O
在Rt△ABC和Rt△DCB中
AB=DC
∠ABC=∠DCB
BC=CB
∴ Rt△ABC≌Rt△DCB (SAS)
∴AC=BD (全等三角形对应边相等)
3、如果矩形的一条对角线长为8cm,两条对角线的一个交角为120°,求矩形的边长(精确到0.01cm)。
A
B
C
D
O
解:∵∠AOD=120°
∴∠AOB=60°
∵ AO=BO=CO
∴ △AOB是等边三角形。
∴ AB=AO=8÷2=4cm
3、如果矩形的一条对角线长为8cm,两条对角线的一个交角为120°,求矩形的边长(精确到0.01cm)。
A
B
C
D
O
在Rt△ABC中
BC=
答:矩形的边长分别是4cm和
矩形的判定方法
由矩形的定义可知:
有一个角是直角的平行四边形是矩形。
当平行四边形的一角变为直角时,另外三个角同时都变为直角,也使两条对角线成为相等的线段。
矩形的判定方法
由矩形的定义可知:
有一个角是直角的平行四边形是矩形。
矩形的判定定理:
对角线相等的平行四边形是矩形。
矩形的判定定理:
对角线相等的平行四边形是矩形。
已知:□ ABCD,且AC=BD
求证: □ ABCD是矩形。
证明:∵□ ABCD
A
B
C
D
O
∴ AD=BC
AD∥BC
在△ABC和△BAD中
在△ABC和△BAD中
A
B
C
D
O
AB=BA
AC=BD
AD=BC
∴ △ABC≌△BAD (SSS)
∴ ∠ABC=∠BAD
∵ AD∥BC
∴ ∠ABC+∠BAD =180°
A
B
C
D
O
∴ △ABC≌△BAD (SSS)
∴ ∠ABC=∠BAD
∵ AD∥BC
∴ ∠ABC+∠BAD =180°
∴ ∠ABC=∠BAD =90°
∴ 四边形ABCD是矩形。
工人师傅在做门窗或矩形零件时,不仅要测量两组对边的长度是否相等,常常还要测量它们的两条对角线是否相等,以确保图形是矩形,你知道其中的道理吗?
⑴两组对边相等的四边形是平行四边形;
⑵对角线相等的平行四边形是矩形。
答:量两组对边的长度可知是否为平行四边形;
量两条对角线是否相等可知是否为矩形。
思考
如图,李芳同学用画“边——直角、边——直角、边——直角、边”这样四步画出了一个四边形,她说这就是一个矩形,她的判断对吗?你能证明吗?
边
直角
边
直角
边
直角
边
矩形的判定方法
有三个角是直角的四边形是矩形。
由此,我又得到了矩形的一个判定定理:
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形。
随堂练习
1、八年级⑶班的同学要在广场上布置一个矩形的花坛。计划用“串红”摆成两条对角线。如果一条对角线用了38盆“串红”,还需要从花房运来多少盆“串红”?为什么?如果一条对角线用了49盆呢?为什么?
⑴还要38盆。
⑵还要48盆就够了。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
