第九章 中心对称图形--平行四边形单元检测试题(含解析)
文档属性
| 名称 | 第九章 中心对称图形--平行四边形单元检测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-12 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
苏科版八年级下册第九章中心对称图形--平行四边形
单元测试(A卷)
(时间100分钟,总分100分)
一、选择题(共10小题,每小题3分,满分30分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )
A.(3,1) B.(3,﹣1) C.(1,﹣3) D.(1,3)
3.若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形 B.对角线相互垂直的四边形
C.正方形 D.对角线相等的四边形
4.已知 ABCD中,∠A+∠C=240°,则∠B的度数是( )
A.100° B.60° C.80° D.160°
5.有下列四个命题,其中正确的个数为( )
①两条对角线互相平分的四边形是平行四边形;
②一条对角线平分一个内角的平行四边形是菱形;
③两条对角线互相垂直的平行四边形是矩形;
④两条对角线相等且互相垂直的四边形是正方形.
A.4 B.3 C.2 D.1
6.一个四边形,对于下列条件:①一组对边平行,一组对角相等;②一组对边平行,一条对角线被另一条对角线平分;③一组对边相等,一条对角线被另一条对角线平分;④两组对角的平分线分别平行,不能判定为平行四边形的是( )
A.① B.② C.③ D.④
7.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
8.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )
A.6 B.4 C.3 D.2
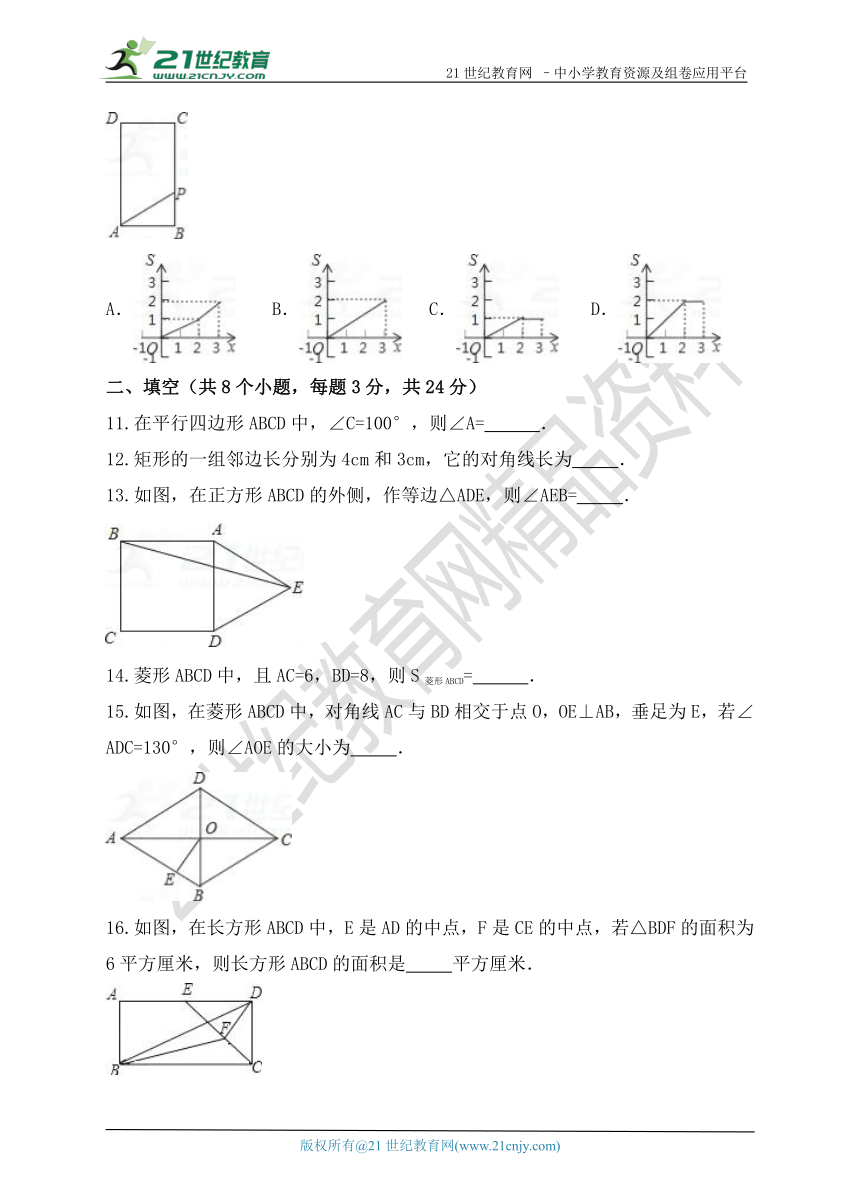
9..如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )
A.2 B.3 C. D.6
10.如图,矩形ABCD中,AB=1,BC=2,点P从点B出发,沿B→C→D向终点D匀速运动,设点P走过的路程为x,△ABP的面积为S,能正确反映S与x之间函数关系的图象是( )
A. B. C. D.
二、填空(共8个小题,每题3分,共24分)
11.在平行四边形ABCD中,∠C=100°,则∠A= .
12.矩形的一组邻边长分别为4cm和3cm,它的对角线长为 .
13.如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB= .
14.菱形ABCD中,且AC=6,BD=8,则S菱形ABCD= .
15.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为 .
16.如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是 平方厘米.
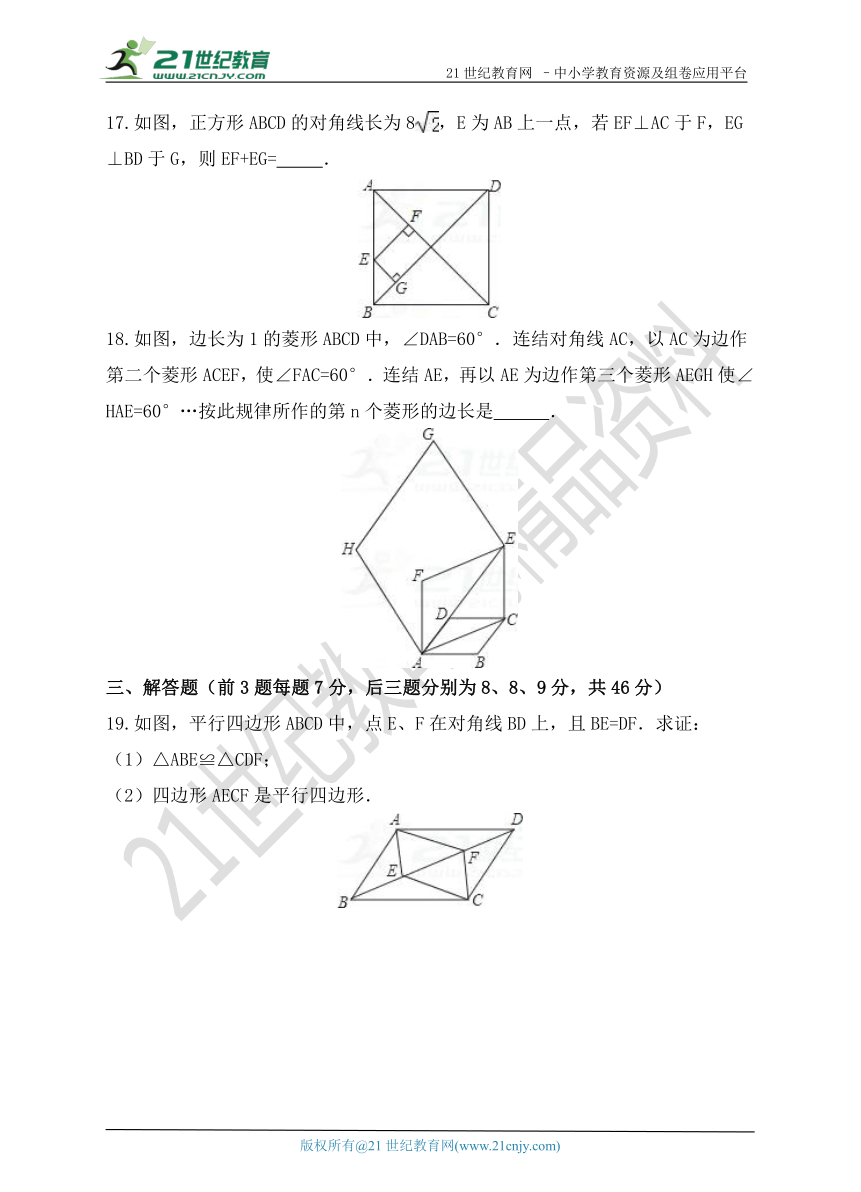
17.如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= .
18.如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 .
三、解答题(前3题每题7分,后三题分别为8、8、9分,共46分)
19.如图,平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
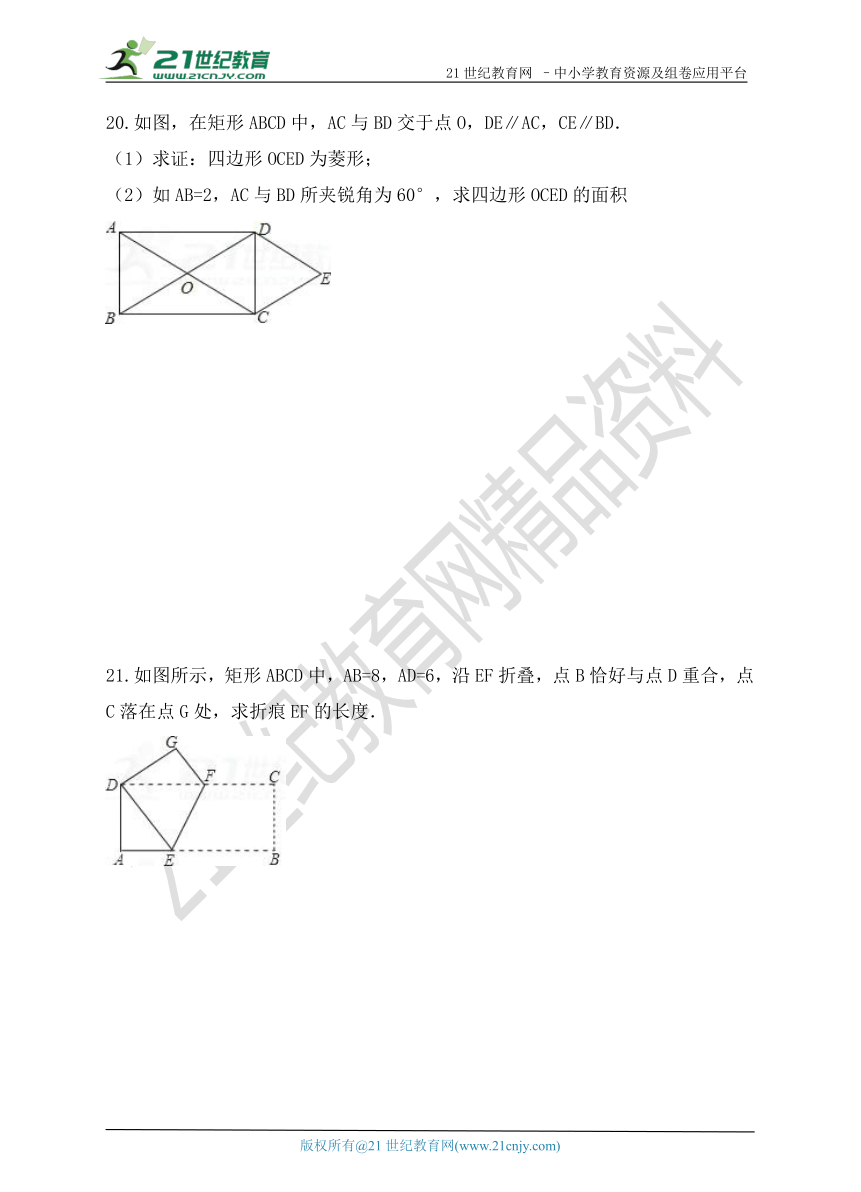
20.如图,在矩形ABCD中,AC与BD交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)如AB=2,AC与BD所夹锐角为60°,求四边形OCED的面积
21.如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
22.如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.
23.如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
24.课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:
延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形或全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)问题解决:
受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(3)问题拓展:
如图3,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作∠EDF为60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
参考答案:
一、选择题(共10小题,每小题3分,满分30分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
【考点】中心对称图形.
【分析】根据中心对称的定义,结合所给图形即可作出判断.
【解答】解:A、是中心对称图形,故本选项正确;
B、不是中心对称图形,故本选项错误;
C、不是中心对称图形,故本选项错误;
D、不是中心对称图形,故本选项错误;
故选:A.
2.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )
A.(3,1) B.(3,﹣1) C.(1,﹣3) D.(1,3)
【考点】菱形的性质;坐标与图形性质.
【分析】首先连接AB交OC于点D,由四边形OACB是菱形,可得AB⊥OC,AD=BD=1,OD=CD=3,易得点B的坐标是(3,﹣1).
【解答】解:连接AB交OC于点D,
∵四边形OACB是菱形,
∴AB⊥OC,AD=BD=1,OD=CD=3,
∴点B的坐标是(3,﹣1).
故选:B.
3.若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形 B.对角线相互垂直的四边形
C.正方形 D.对角线相等的四边形
【考点】矩形的判定;三角形中位线定理.
【分析】此题要根据矩形的性质和三角形中位线定理求解;首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.
【解答】解:已知:如右图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形ABCD是对角线垂直的四边形.
证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是矩形,即EF⊥FG,
∴AC⊥BD;故选B.
【点评】本题主要利用了矩形的性质和三角形中位线定理来求解.
4.已知 ABCD中,∠A+∠C=240°,则∠B的度数是( )
A.100° B.60° C.80° D.160°
【考点】平行四边形的性质.
【分析】由四边形ABCD是平行四边形,可得∠A=∠C,AD∥BC,又由∠A+∠B=200°,即可求得∠A的度数,继而求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∵∠A+∠C=240°,
∴∠A=120°,
∴∠B=180°﹣∠A=60°.
故选B.
5.有下列四个命题,其中正确的个数为( )
①两条对角线互相平分的四边形是平行四边形;
②一条对角线平分一个内角的平行四边形是菱形;
③两条对角线互相垂直的平行四边形是矩形;
④两条对角线相等且互相垂直的四边形是正方形.
A.4 B.3 C.2 D.1
【考点】命题与定理.
【分析】根据平行四边形、矩形、菱形、以及正方形的判定方法逐一判定即可.
【解答】解:①两条对角线互相平分的四边形是平行四边形;正确;
②一条对角线平分一个内角的平行四边形是菱形;正确;
③两条对角线互相垂直的平行四边形是矩形;错误;
④两条对角线相等且互相垂直的四边形是正方形;错误;
正确的个数为2个;
故选:C.
【点评】本题考查了命题与定理、平行四边形、矩形、菱形、以及正方形的判定方法;熟记平行四边形、矩形、菱形、以及正方形的判定方法是解决问题的关键.
6.一个四边形,对于下列条件:①一组对边平行,一组对角相等;②一组对边平行,一条对角线被另一条对角线平分;③一组对边相等,一条对角线被另一条对角线平分;④两组对角的平分线分别平行,不能判定为平行四边形的是( )
A.① B.② C.③ D.④
【考点】平行四边形的判定.
【分析】一组对边平行,一组对角相等可推出两组对角分别相等,可判定为平行四边形一组对边平行,一条对角线被另一条对角线平分,可利用全等得出这组对边也相等,可判定为平行四边形一组对边相等,一条对角线被另一条对角线平分,所在的三角形不能得出一定全等,所以能判定为平行四边形.
【解答】解:根据平行四边形的判定,能满足是平行四边形条件的有:①,②、④,而③无法判定.
故选:C.
【点评】本题考查了平行四边形的判定,平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
7.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
【考点】正方形的判定;平行四边形的性质;菱形的判定;矩形的判定.
【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.
【解答】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、∵四边形ABCD是平行四边形,∴BO=OD,∵AC⊥BD,∴AB2=BO2+AO2,AD2=DO2+AO2,∴AB=AD,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;
综上所述,符合题意是D选项;
故选:D.
8.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )
A.6 B.4 C.3 D.2
【考点】三角形中位线定理;平行四边形的性质.
【分析】根据AC+BD=24厘米,可得出出OA+OB=12cm,继而求出AB,判断EF是△OAB的中位线即可得出EF的长度.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AC+BD=24厘米,
∴OA+OB=12cm,
∵△OAB的周长是18厘米,
∴AB=6cm,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=AB=3cm.
故选C.
【点评】本题考查了三角形的中位线定理,解答本题需要用到:平行四边形的对角线互相平分,三角形中位线的判定定理及性质.
9..如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )
A.2 B.3 C. D.6【考点】正方形的性质;全等三角形的判定与性质;矩形的判定与性质.
【分析】根据正方形的四条边都相等可得AB=AD,正方形的对角线平分一组对角可得∠BAC=∠DAC=45°,然后利用“边角边”证明△ABP和△ADP全等,根据全等三角形对应边相等证明即可;求出四边形BFPE是矩形,根据矩形的对角线相等可EF=PB.即可.
【解答】解:如图,连接PB,
在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,
在△ABP和△ADP中,
∴△ABP≌△ADP(SAS),
∴BP=DP;
∵PE⊥AB,PF⊥BC,∠ABC=90°,
∴四边形BFPE是矩形,
∴EF=PB,
∴EF=DP=3,
故选B
【点评】本题考查了正方形的性质,全等三角形的判定与性质,矩形的判定与性质,熟记正方形的性质得到三角形全等的条件是解题的关键
10.如图,矩形ABCD中,AB=1,BC=2,点P从点B出发,沿B→C→D向终点D匀速运动,设点P走过的路程为x,△ABP的面积为S,能正确反映S与x之间函数系的图象是( )
A. B. C. D.
【考点】动点问题的函数图象.
【分析】要找出准确反映s与x之间对应关系的图象,需分析在不同阶段中s随x变化的情况.
【解答】解:由题意知,点P从点B出发,沿B→C→D向终点D匀速运动,则
当0<x≤2,s=,
当2<x≤3,s=1,
由以上分析可知,这个分段函数的图象开始直线一部分,最后为水平直线的一部分.
故选C.
二、填空(共8个小题,每题3分,共24分)
11.在平行四边形ABCD中,∠C=100°,则∠A= 100° .
【考点】平行四边形的性质.
【分析】由平行四边形的对角相等即可得出结果.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C=100°;
故答案为:100°.
【点评】本题考查了平行四边形的性质;熟记平行四边形的对角相等是解决问题的关键.
12.矩形的一组邻边长分别为4cm和3cm,它的对角线长为 5cm .
【考点】矩形的性质.
【分析】由矩形的性质得出AC=BD,∠ABC=90°,再由勾股定理求出AC即可.
【解答】解:如图所示:
∵四边形ABCD是矩形,
∴AC=BD,∠ABC=90°,
∵AB=3cm,BC=4cm,
∴BD=AC===5(cm);
故答案为:5cm.
【点评】本题考查了矩形的性质、勾股定理;熟练掌握矩形的性质,由勾股定理求出AC是解决问题的关键.
13.如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB= 15° .
【考点】正方形的性质;等边三角形的性质.
【分析】由四边形ABCD为正方形,三角形ADE为等比三角形,可得出正方形的四条边相等,三角形的三边相等,进而得到AB=AE,且得到∠BAD为直角,∠DAE为60°,由∠BAD+∠DAE求出∠BAE的度数,进而利用等腰三角形的性质及三角形的内角和定理即可求出∠AEB的度数.
【解答】解:∵四边形ABCD为正方形,△ADE为等边三角形,
∴AB=BC=CD=AD=AE=DE,∠BAD=90°,∠DAE=60°,
∴∠BAE=∠BAD+∠DAE=150°,
又∵AB=AE,
∴∠AEB==15°.
故答案为:15°.
【点评】此题考查了正方形的性质,以及等边三角形的性质,利用了等量代换的思想,熟练掌握性质是解本题的关键.
14.菱形ABCD中,且AC=6,BD=8,则S菱形ABCD= 24 .
【考点】菱形的性质.
【分析】由菱形ABCD中,且AC=6,BD=8,根据菱形的面积等于对角线积的一半,即可求得答案.
【解答】解:∵菱形ABCD中,且AC=6,BD=8,
∴S菱形ABCD=ACBD=24.
故答案为:24.
【点评】此题考查了菱形的性质.注意菱形的面积等于对角线积的一半.
15.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为 65° .
【考点】菱形的性质.
【分析】先根据菱形的邻角互补求出∠BAD的度数,再根据菱形的对角线平分一组对角求出∠BAO的度数,然后根据直角三角形两锐角互余列式计算即可得解.
【解答】解:在菱形ABCD中,∠ADC=130°,
∴∠BAD=180°﹣130°=50°,
∴∠BAO=∠BAD=×50°=25°,
∵OE⊥AB,
∴∠AOE=90°﹣∠BAO=90°﹣25°=65°.
故答案为:65°.
16.如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是48平方厘米.
【考点】矩形的性质;三角形的面积;全等三角形的判定与性质.
【专题】计算题.
【分析】延长DF交BC于G,证出△DEF≌△GCF,根据全等得出DE=CG=BG,DF=GF,即可求出S△BDG=2S△BDF,S长方形ABCD=4S△BDG,代入求出即可.
【解答】解:延长DF交BC于G,
∵E是AD的中点,F是CE的中点,
∴EF=FC,AE=DE,
∵四边形ABCD是长方形,
∴BC=AD=2DE,AD∥BC,
∴∠DEF=∠FCG,
在△DEF和△GCF中
∴△DEF≌△GCF(ASA),
∴DE=CG=BG,DF=GF,
∴S△BDG=2S△BDF=12平方厘米,
∴S长方形ABCD=4S△BDG=48平方厘米,
∴长方形ABCD的面积是48平方厘米.
故答案为:48.
【点评】本题主要考查了矩形的性质,全等三角形的性质和判定,三角形的面积等知识点,根据求出△DEF≌△GCF是解此题的关键.
17.如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= 4 .
【考点】正方形的性质.
【分析】正方形ABCD的对角线交于点O,连接0E,由正方形的性质和对角线长为8,得出OA=OB=4;进一步利用S△ABO=S△AEO+S△EBO,整理得出答案解决问题.
【解答】解:如图:
∵四边形ABCD是正方形,
∴OA=OB=4,
又∵S△ABO=S△AEO+S△EBO,
∴OAOB=OAEF+OBEG,
即×4×4=×4×(EF+EG)
∴EF+EG=4.
故答案为:4.
【点评】此题考查正方形的性质,三角形的面积计算公式;利用三角形的面积巧妙建立所求线段与已知线段的关系,进一步解决问题.
18.如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 ()n﹣1 .
【考点】菱形的性质.
【分析】连接DB于AC相交于M,根据已知和菱形的性质可分别求得AC,AE,AG的长,从而可发现规律根据规律不难求得第n个菱形的边长.
【解答】解:连接DB,
∵四边形ABCD是菱形,
∴AD=AB.AC⊥DB,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴DB=AD=1,
∴BM=,
∴AM=,
∴AC=,
同理可得AE=AC=()2,AG=AE=3=()3,
按此规律所作的第n个菱形的边长为()n﹣1,
故答案为()n﹣1
【点评】此题主要考查菱形的性质、等边三角形的判定和性质以及学生探索规律的能力.三、解答题(前3题每题7分,后三题分别为8、8、9分,共46分)
19.如图,平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
【考点】平行四边形的判定与性质;全等三角形的判定与性质.
【分析】(1)根据平行四边形平行四边形的性质得到AB∥CD AB=CD,从而得到∠ABE=∠CDF,然后利用SAS证得两三角形全等即可;
(2)利用(1)中的全等三角形的对应角相等推知∠AEB=∠DFC,则等角的补角相等,即∠AEF=∠CFE,所以AE∥FC.根据“有一组对边平行且相等”证得结论.
【解答】证明(1)∵四边形ABCD是平行四边形,
∴AB∥CD AB=CD,
∴∠ABE=∠CDF,
∵BE=DF,
∴△ABE≌△CDF (SAS);
(2)证明:∵由(1)知,△ABE≌△CDF,
∴BE=DF,∠AEB=∠DFC,
∴∠AEF=∠CFE,
∴AE∥FC,
∴四边形AECF是平行四边形.
【点评】本题考查了全等三角形的判定与性质,平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法. 20.如图,在矩形ABCD中,AC与BD交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)如AB=2,AC与BD所夹锐角为60°,求四边形OCED的面积
【考点】矩形的性质;菱形的判定.
【分析】(1)先根据DE∥AC、CE∥BD判定四边形ODEC是平行四边形,然后根据矩形的性质:矩形的对角线相等且互相平分,可得OC=OD,由此可判定四边形OCED是菱形.
(2)作DM⊥OC,垂足为点M,证明△COD为等边三角形,得出OC=CD=OD=2,得出CM=1,DM=CM=,菱形OCED面积=OCDM,即可得出结果.
【解答】(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD为矩形,
∴AC=BD,OC=AC,OD=BD,
∴OC=OD,
∴四边形OCED为菱形;
(2)解:作DM⊥OC,垂足为点M,
∵OC=OD,∠COD=60°,
∴△COD为等边三角形,
∴OC=CD=OD,
∵AB=2,四边形ABCD是矩形,
∴CD=AB=2,
∴OC=CD=OD=2,
∵DM⊥OC,
∴CM=1,
∴DM=CM=,
∴菱形OCED面积=OCDM=2.
【点评】本题主要考查矩形的性质,平行四边形的判定、菱形的判定、等边三角形的判定与性质;熟练掌握矩形的性质和菱形的判定,证明三角形是等边三角形是解决问题(2)的关键.
21.如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
【考点】矩形的性质;翻折变换(折叠问题).
【分析】作EM⊥CD,垂足为点M设DE=x,由折叠的性质得出∠DEF=∠BEF,BE=DE=x,得出AE=8﹣x,再由矩形的性质得出∠DEF=∠DFE,证出DE=DF,在Rt△ADE中,由勾股定理得出方程,解方程求出DE,得出AE、MF,由勾股定理求出EF即可.
【解答】解:作EM⊥CD,垂足为点M,如图所示:
设DE=x,
由折叠的性质得:∠DEF=∠BEF,BE=DE=x,
∴AE=8﹣x,
∵四边形ABCD是矩形,
∴∠A=90°,AB∥CD,
∴∠DFE=∠BEF,
∴∠DEF=∠DFE,
∴DE=DF,
在Rt△ADE中,由勾股定理得:(8﹣x)2+62=x2,
解得:x=,
∴AE=DM=8﹣=,
又∵DF=DE=,
∴MF=DF﹣DM=﹣=,
又∵ME=AD=6,
∴EF===.
【点评】此题主要考查了翻折变换的性质矩形的性质、勾股定理、等腰三角形的判定;熟练掌握翻折变换和矩形的性质,由勾股定理得出方程求出BE是解决问题的关键.
22.如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.
【考点】平行四边形的判定与性质;全等三角形的性质.
【分析】首先连接BD,交AC于点O,由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,即可求得OA=OC,OB=OD,又由AE=CF,可得OE=OF,然后根据对角线互相相平分的四边形是平行四边形.
【解答】证明:连接BD,交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形DEBF是平行四边形.
【点评】此题考查了平行四边形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
23.如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
【考点】平行四边形的判定与性质;全等三角形的判定与性质;矩形的判定.
【专题】证明题.
【分析】(1)先由已知平行四边形ABCD得出AB∥DC,AB=DC, ∠ABF=∠ECF,从而证得△ABF≌△ECF;
(2)由(1)得的结论先证得四边形ABEC是平行四边形,通过角的关系得出FA=FE=FB=FC,AE=BC,得证.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠ABF=∠ECF,
∵EC=DC,∴AB=EC,
在△ABF和△ECF中,
∵∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,
∴△ABF≌△ECF(AAS).
(2)∵AB=EC,AB∥EC,
∴四边形ABEC是平行四边形,
∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,
∴∠ABC=∠D,
又∵∠AFC=2∠D,
∴∠AFC=2∠ABC,
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
【点评】此题考查的知识点是平行四边形的判定与性质,全等三角形的判定和性质及矩形的判定,关键是先由平行四边形的性质证三角形全等,然后推出平行四边形通过角的关系证矩形.
24.课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:
延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形或全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)问题解决:
受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(3)问题拓展:
如图3,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作∠EDF为60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
【考点】几何变换综合题.
【分析】(2)①首先延长FD到G,使得DG=DF,进而得出CF=BG,DF=DG,以及EF=EG,再利用三角形三边关系得出答案;
②由①知∠FCD=∠DBG,EF=EG,再利用勾股定理得出答案;
(3)利用全等三角形的判定与性质得出△DEG≌△DEF(SAS),进而得出EF=EG=BE+BG,即EF=BE+CF,进而得出答案.
【解答】(2)证明:①如答题图1,延长FD到G,使得DG=DF,连接BG、EG.
则CF=BG,DF=DG,
∵DE⊥DF,∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
解:②若∠A=90°,则∠EBC+∠FCB=90°,
由①知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
∴BE2+CF2=EF2;
(3)解:如答题图2,将△DCF绕点D逆时针旋转120°得到△DBG.
∵∠C+∠ABD=180°,∠4=∠C,
∴∠4+∠ABD=180°,
∴点E、B、G在同一直线上.
∵∠3=∠1,∠BDC=120°,∠EDF=60°,
∴∠1+∠2=60°,故∠2+∠3=60°,即∠EDG=60°
∴∠EDF=∠EDG=60°,
在△DEG和△DEF中,
∴△DEG≌△DEF(SAS),
∴EF=EG=BE+BG,即EF=BE+CF.
【点评】此题主要考查了几何变换综合以及全等三角形的判定与性质、勾股定理等知识,正确得出△DEG≌△DEF(SAS)是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
苏科版八年级下册第九章中心对称图形--平行四边形
单元测试(A卷)
(时间100分钟,总分100分)
一、选择题(共10小题,每小题3分,满分30分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )
A.(3,1) B.(3,﹣1) C.(1,﹣3) D.(1,3)
3.若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形 B.对角线相互垂直的四边形
C.正方形 D.对角线相等的四边形
4.已知 ABCD中,∠A+∠C=240°,则∠B的度数是( )
A.100° B.60° C.80° D.160°
5.有下列四个命题,其中正确的个数为( )
①两条对角线互相平分的四边形是平行四边形;
②一条对角线平分一个内角的平行四边形是菱形;
③两条对角线互相垂直的平行四边形是矩形;
④两条对角线相等且互相垂直的四边形是正方形.
A.4 B.3 C.2 D.1
6.一个四边形,对于下列条件:①一组对边平行,一组对角相等;②一组对边平行,一条对角线被另一条对角线平分;③一组对边相等,一条对角线被另一条对角线平分;④两组对角的平分线分别平行,不能判定为平行四边形的是( )
A.① B.② C.③ D.④
7.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
8.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )
A.6 B.4 C.3 D.2
9..如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )
A.2 B.3 C. D.6
10.如图,矩形ABCD中,AB=1,BC=2,点P从点B出发,沿B→C→D向终点D匀速运动,设点P走过的路程为x,△ABP的面积为S,能正确反映S与x之间函数关系的图象是( )
A. B. C. D.
二、填空(共8个小题,每题3分,共24分)
11.在平行四边形ABCD中,∠C=100°,则∠A= .
12.矩形的一组邻边长分别为4cm和3cm,它的对角线长为 .
13.如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB= .
14.菱形ABCD中,且AC=6,BD=8,则S菱形ABCD= .
15.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为 .
16.如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是 平方厘米.
17.如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= .
18.如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 .
三、解答题(前3题每题7分,后三题分别为8、8、9分,共46分)
19.如图,平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
20.如图,在矩形ABCD中,AC与BD交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)如AB=2,AC与BD所夹锐角为60°,求四边形OCED的面积
21.如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
22.如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.
23.如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
24.课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:
延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形或全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)问题解决:
受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(3)问题拓展:
如图3,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作∠EDF为60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
参考答案:
一、选择题(共10小题,每小题3分,满分30分)
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
【考点】中心对称图形.
【分析】根据中心对称的定义,结合所给图形即可作出判断.
【解答】解:A、是中心对称图形,故本选项正确;
B、不是中心对称图形,故本选项错误;
C、不是中心对称图形,故本选项错误;
D、不是中心对称图形,故本选项错误;
故选:A.
2.菱形OACB在平面直角坐标系中的位置如图所示,点C的坐标是(6,0),点A的纵坐标是1,则点B的坐标是( )
A.(3,1) B.(3,﹣1) C.(1,﹣3) D.(1,3)
【考点】菱形的性质;坐标与图形性质.
【分析】首先连接AB交OC于点D,由四边形OACB是菱形,可得AB⊥OC,AD=BD=1,OD=CD=3,易得点B的坐标是(3,﹣1).
【解答】解:连接AB交OC于点D,
∵四边形OACB是菱形,
∴AB⊥OC,AD=BD=1,OD=CD=3,
∴点B的坐标是(3,﹣1).
故选:B.
3.若顺次连接四边形ABCD各边中点所得四边形是矩形,则四边形ABCD必然是( )
A.菱形 B.对角线相互垂直的四边形
C.正方形 D.对角线相等的四边形
【考点】矩形的判定;三角形中位线定理.
【分析】此题要根据矩形的性质和三角形中位线定理求解;首先根据三角形中位线定理知:所得四边形的对边都平行且相等,那么其必为平行四边形,若所得四边形是矩形,那么邻边互相垂直,故原四边形的对角线必互相垂直,由此得解.
【解答】解:已知:如右图,四边形EFGH是矩形,且E、F、G、H分别是AB、BC、CD、AD的中点,求证:四边形ABCD是对角线垂直的四边形.
证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是矩形,即EF⊥FG,
∴AC⊥BD;故选B.
【点评】本题主要利用了矩形的性质和三角形中位线定理来求解.
4.已知 ABCD中,∠A+∠C=240°,则∠B的度数是( )
A.100° B.60° C.80° D.160°
【考点】平行四边形的性质.
【分析】由四边形ABCD是平行四边形,可得∠A=∠C,AD∥BC,又由∠A+∠B=200°,即可求得∠A的度数,继而求得答案.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD∥BC,
∵∠A+∠C=240°,
∴∠A=120°,
∴∠B=180°﹣∠A=60°.
故选B.
5.有下列四个命题,其中正确的个数为( )
①两条对角线互相平分的四边形是平行四边形;
②一条对角线平分一个内角的平行四边形是菱形;
③两条对角线互相垂直的平行四边形是矩形;
④两条对角线相等且互相垂直的四边形是正方形.
A.4 B.3 C.2 D.1
【考点】命题与定理.
【分析】根据平行四边形、矩形、菱形、以及正方形的判定方法逐一判定即可.
【解答】解:①两条对角线互相平分的四边形是平行四边形;正确;
②一条对角线平分一个内角的平行四边形是菱形;正确;
③两条对角线互相垂直的平行四边形是矩形;错误;
④两条对角线相等且互相垂直的四边形是正方形;错误;
正确的个数为2个;
故选:C.
【点评】本题考查了命题与定理、平行四边形、矩形、菱形、以及正方形的判定方法;熟记平行四边形、矩形、菱形、以及正方形的判定方法是解决问题的关键.
6.一个四边形,对于下列条件:①一组对边平行,一组对角相等;②一组对边平行,一条对角线被另一条对角线平分;③一组对边相等,一条对角线被另一条对角线平分;④两组对角的平分线分别平行,不能判定为平行四边形的是( )
A.① B.② C.③ D.④
【考点】平行四边形的判定.
【分析】一组对边平行,一组对角相等可推出两组对角分别相等,可判定为平行四边形一组对边平行,一条对角线被另一条对角线平分,可利用全等得出这组对边也相等,可判定为平行四边形一组对边相等,一条对角线被另一条对角线平分,所在的三角形不能得出一定全等,所以能判定为平行四边形.
【解答】解:根据平行四边形的判定,能满足是平行四边形条件的有:①,②、④,而③无法判定.
故选:C.
【点评】本题考查了平行四边形的判定,平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
7.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
【考点】正方形的判定;平行四边形的性质;菱形的判定;矩形的判定.
【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.
【解答】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;
B、∵四边形ABCD是平行四边形,∴BO=OD,∵AC⊥BD,∴AB2=BO2+AO2,AD2=DO2+AO2,∴AB=AD,∴四边形ABCD是菱形,故B选项正确;
C、有一个角是直角的平行四边形是矩形,故C选项正确;
D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;
综上所述,符合题意是D选项;
故选:D.
8.如图,□ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )
A.6 B.4 C.3 D.2
【考点】三角形中位线定理;平行四边形的性质.
【分析】根据AC+BD=24厘米,可得出出OA+OB=12cm,继而求出AB,判断EF是△OAB的中位线即可得出EF的长度.
【解答】解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
又∵AC+BD=24厘米,
∴OA+OB=12cm,
∵△OAB的周长是18厘米,
∴AB=6cm,
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线,
∴EF=AB=3cm.
故选C.
【点评】本题考查了三角形的中位线定理,解答本题需要用到:平行四边形的对角线互相平分,三角形中位线的判定定理及性质.
9..如图,在正方形ABCD中,点P在AC上,PE⊥AB,PF⊥BC,垂足分别为E、F,EF=3,则PD的长为( )
A.2 B.3 C. D.6【考点】正方形的性质;全等三角形的判定与性质;矩形的判定与性质.
【分析】根据正方形的四条边都相等可得AB=AD,正方形的对角线平分一组对角可得∠BAC=∠DAC=45°,然后利用“边角边”证明△ABP和△ADP全等,根据全等三角形对应边相等证明即可;求出四边形BFPE是矩形,根据矩形的对角线相等可EF=PB.即可.
【解答】解:如图,连接PB,
在正方形ABCD中,AB=AD,∠BAC=∠DAC=45°,
在△ABP和△ADP中,
∴△ABP≌△ADP(SAS),
∴BP=DP;
∵PE⊥AB,PF⊥BC,∠ABC=90°,
∴四边形BFPE是矩形,
∴EF=PB,
∴EF=DP=3,
故选B
【点评】本题考查了正方形的性质,全等三角形的判定与性质,矩形的判定与性质,熟记正方形的性质得到三角形全等的条件是解题的关键
10.如图,矩形ABCD中,AB=1,BC=2,点P从点B出发,沿B→C→D向终点D匀速运动,设点P走过的路程为x,△ABP的面积为S,能正确反映S与x之间函数系的图象是( )
A. B. C. D.
【考点】动点问题的函数图象.
【分析】要找出准确反映s与x之间对应关系的图象,需分析在不同阶段中s随x变化的情况.
【解答】解:由题意知,点P从点B出发,沿B→C→D向终点D匀速运动,则
当0<x≤2,s=,
当2<x≤3,s=1,
由以上分析可知,这个分段函数的图象开始直线一部分,最后为水平直线的一部分.
故选C.
二、填空(共8个小题,每题3分,共24分)
11.在平行四边形ABCD中,∠C=100°,则∠A= 100° .
【考点】平行四边形的性质.
【分析】由平行四边形的对角相等即可得出结果.
【解答】解:∵四边形ABCD是平行四边形,
∴∠A=∠C=100°;
故答案为:100°.
【点评】本题考查了平行四边形的性质;熟记平行四边形的对角相等是解决问题的关键.
12.矩形的一组邻边长分别为4cm和3cm,它的对角线长为 5cm .
【考点】矩形的性质.
【分析】由矩形的性质得出AC=BD,∠ABC=90°,再由勾股定理求出AC即可.
【解答】解:如图所示:
∵四边形ABCD是矩形,
∴AC=BD,∠ABC=90°,
∵AB=3cm,BC=4cm,
∴BD=AC===5(cm);
故答案为:5cm.
【点评】本题考查了矩形的性质、勾股定理;熟练掌握矩形的性质,由勾股定理求出AC是解决问题的关键.
13.如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB= 15° .
【考点】正方形的性质;等边三角形的性质.
【分析】由四边形ABCD为正方形,三角形ADE为等比三角形,可得出正方形的四条边相等,三角形的三边相等,进而得到AB=AE,且得到∠BAD为直角,∠DAE为60°,由∠BAD+∠DAE求出∠BAE的度数,进而利用等腰三角形的性质及三角形的内角和定理即可求出∠AEB的度数.
【解答】解:∵四边形ABCD为正方形,△ADE为等边三角形,
∴AB=BC=CD=AD=AE=DE,∠BAD=90°,∠DAE=60°,
∴∠BAE=∠BAD+∠DAE=150°,
又∵AB=AE,
∴∠AEB==15°.
故答案为:15°.
【点评】此题考查了正方形的性质,以及等边三角形的性质,利用了等量代换的思想,熟练掌握性质是解本题的关键.
14.菱形ABCD中,且AC=6,BD=8,则S菱形ABCD= 24 .
【考点】菱形的性质.
【分析】由菱形ABCD中,且AC=6,BD=8,根据菱形的面积等于对角线积的一半,即可求得答案.
【解答】解:∵菱形ABCD中,且AC=6,BD=8,
∴S菱形ABCD=ACBD=24.
故答案为:24.
【点评】此题考查了菱形的性质.注意菱形的面积等于对角线积的一半.
15.如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为 65° .
【考点】菱形的性质.
【分析】先根据菱形的邻角互补求出∠BAD的度数,再根据菱形的对角线平分一组对角求出∠BAO的度数,然后根据直角三角形两锐角互余列式计算即可得解.
【解答】解:在菱形ABCD中,∠ADC=130°,
∴∠BAD=180°﹣130°=50°,
∴∠BAO=∠BAD=×50°=25°,
∵OE⊥AB,
∴∠AOE=90°﹣∠BAO=90°﹣25°=65°.
故答案为:65°.
16.如图,在长方形ABCD中,E是AD的中点,F是CE的中点,若△BDF的面积为6平方厘米,则长方形ABCD的面积是48平方厘米.
【考点】矩形的性质;三角形的面积;全等三角形的判定与性质.
【专题】计算题.
【分析】延长DF交BC于G,证出△DEF≌△GCF,根据全等得出DE=CG=BG,DF=GF,即可求出S△BDG=2S△BDF,S长方形ABCD=4S△BDG,代入求出即可.
【解答】解:延长DF交BC于G,
∵E是AD的中点,F是CE的中点,
∴EF=FC,AE=DE,
∵四边形ABCD是长方形,
∴BC=AD=2DE,AD∥BC,
∴∠DEF=∠FCG,
在△DEF和△GCF中
∴△DEF≌△GCF(ASA),
∴DE=CG=BG,DF=GF,
∴S△BDG=2S△BDF=12平方厘米,
∴S长方形ABCD=4S△BDG=48平方厘米,
∴长方形ABCD的面积是48平方厘米.
故答案为:48.
【点评】本题主要考查了矩形的性质,全等三角形的性质和判定,三角形的面积等知识点,根据求出△DEF≌△GCF是解此题的关键.
17.如图,正方形ABCD的对角线长为8,E为AB上一点,若EF⊥AC于F,EG⊥BD于G,则EF+EG= 4 .
【考点】正方形的性质.
【分析】正方形ABCD的对角线交于点O,连接0E,由正方形的性质和对角线长为8,得出OA=OB=4;进一步利用S△ABO=S△AEO+S△EBO,整理得出答案解决问题.
【解答】解:如图:
∵四边形ABCD是正方形,
∴OA=OB=4,
又∵S△ABO=S△AEO+S△EBO,
∴OAOB=OAEF+OBEG,
即×4×4=×4×(EF+EG)
∴EF+EG=4.
故答案为:4.
【点评】此题考查正方形的性质,三角形的面积计算公式;利用三角形的面积巧妙建立所求线段与已知线段的关系,进一步解决问题.
18.如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 ()n﹣1 .
【考点】菱形的性质.
【分析】连接DB于AC相交于M,根据已知和菱形的性质可分别求得AC,AE,AG的长,从而可发现规律根据规律不难求得第n个菱形的边长.
【解答】解:连接DB,
∵四边形ABCD是菱形,
∴AD=AB.AC⊥DB,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴DB=AD=1,
∴BM=,
∴AM=,
∴AC=,
同理可得AE=AC=()2,AG=AE=3=()3,
按此规律所作的第n个菱形的边长为()n﹣1,
故答案为()n﹣1
【点评】此题主要考查菱形的性质、等边三角形的判定和性质以及学生探索规律的能力.三、解答题(前3题每题7分,后三题分别为8、8、9分,共46分)
19.如图,平行四边形ABCD中,点E、F在对角线BD上,且BE=DF.求证:
(1)△ABE≌△CDF;
(2)四边形AECF是平行四边形.
【考点】平行四边形的判定与性质;全等三角形的判定与性质.
【分析】(1)根据平行四边形平行四边形的性质得到AB∥CD AB=CD,从而得到∠ABE=∠CDF,然后利用SAS证得两三角形全等即可;
(2)利用(1)中的全等三角形的对应角相等推知∠AEB=∠DFC,则等角的补角相等,即∠AEF=∠CFE,所以AE∥FC.根据“有一组对边平行且相等”证得结论.
【解答】证明(1)∵四边形ABCD是平行四边形,
∴AB∥CD AB=CD,
∴∠ABE=∠CDF,
∵BE=DF,
∴△ABE≌△CDF (SAS);
(2)证明:∵由(1)知,△ABE≌△CDF,
∴BE=DF,∠AEB=∠DFC,
∴∠AEF=∠CFE,
∴AE∥FC,
∴四边形AECF是平行四边形.
【点评】本题考查了全等三角形的判定与性质,平行四边形的判定与性质.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法. 20.如图,在矩形ABCD中,AC与BD交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED为菱形;
(2)如AB=2,AC与BD所夹锐角为60°,求四边形OCED的面积
【考点】矩形的性质;菱形的判定.
【分析】(1)先根据DE∥AC、CE∥BD判定四边形ODEC是平行四边形,然后根据矩形的性质:矩形的对角线相等且互相平分,可得OC=OD,由此可判定四边形OCED是菱形.
(2)作DM⊥OC,垂足为点M,证明△COD为等边三角形,得出OC=CD=OD=2,得出CM=1,DM=CM=,菱形OCED面积=OCDM,即可得出结果.
【解答】(1)证明:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD为矩形,
∴AC=BD,OC=AC,OD=BD,
∴OC=OD,
∴四边形OCED为菱形;
(2)解:作DM⊥OC,垂足为点M,
∵OC=OD,∠COD=60°,
∴△COD为等边三角形,
∴OC=CD=OD,
∵AB=2,四边形ABCD是矩形,
∴CD=AB=2,
∴OC=CD=OD=2,
∵DM⊥OC,
∴CM=1,
∴DM=CM=,
∴菱形OCED面积=OCDM=2.
【点评】本题主要考查矩形的性质,平行四边形的判定、菱形的判定、等边三角形的判定与性质;熟练掌握矩形的性质和菱形的判定,证明三角形是等边三角形是解决问题(2)的关键.
21.如图所示,矩形ABCD中,AB=8,AD=6,沿EF折叠,点B恰好与点D重合,点C落在点G处,求折痕EF的长度.
【考点】矩形的性质;翻折变换(折叠问题).
【分析】作EM⊥CD,垂足为点M设DE=x,由折叠的性质得出∠DEF=∠BEF,BE=DE=x,得出AE=8﹣x,再由矩形的性质得出∠DEF=∠DFE,证出DE=DF,在Rt△ADE中,由勾股定理得出方程,解方程求出DE,得出AE、MF,由勾股定理求出EF即可.
【解答】解:作EM⊥CD,垂足为点M,如图所示:
设DE=x,
由折叠的性质得:∠DEF=∠BEF,BE=DE=x,
∴AE=8﹣x,
∵四边形ABCD是矩形,
∴∠A=90°,AB∥CD,
∴∠DFE=∠BEF,
∴∠DEF=∠DFE,
∴DE=DF,
在Rt△ADE中,由勾股定理得:(8﹣x)2+62=x2,
解得:x=,
∴AE=DM=8﹣=,
又∵DF=DE=,
∴MF=DF﹣DM=﹣=,
又∵ME=AD=6,
∴EF===.
【点评】此题主要考查了翻折变换的性质矩形的性质、勾股定理、等腰三角形的判定;熟练掌握翻折变换和矩形的性质,由勾股定理得出方程求出BE是解决问题的关键.
22.如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.
【考点】平行四边形的判定与性质;全等三角形的性质.
【分析】首先连接BD,交AC于点O,由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,即可求得OA=OC,OB=OD,又由AE=CF,可得OE=OF,然后根据对角线互相相平分的四边形是平行四边形.
【解答】证明:连接BD,交AC于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OA﹣AE=OC﹣CF,
即OE=OF,
∴四边形DEBF是平行四边形.
【点评】此题考查了平行四边形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
23.如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:△ABF≌△ECF;
(2)若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.
【考点】平行四边形的判定与性质;全等三角形的判定与性质;矩形的判定.
【专题】证明题.
【分析】(1)先由已知平行四边形ABCD得出AB∥DC,AB=DC, ∠ABF=∠ECF,从而证得△ABF≌△ECF;
(2)由(1)得的结论先证得四边形ABEC是平行四边形,通过角的关系得出FA=FE=FB=FC,AE=BC,得证.
【解答】证明:(1)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC,
∴∠ABF=∠ECF,
∵EC=DC,∴AB=EC,
在△ABF和△ECF中,
∵∠ABF=∠ECF,∠AFB=∠EFC,AB=EC,
∴△ABF≌△ECF(AAS).
(2)∵AB=EC,AB∥EC,
∴四边形ABEC是平行四边形,
∴FA=FE,FB=FC,
∵四边形ABCD是平行四边形,
∴∠ABC=∠D,
又∵∠AFC=2∠D,
∴∠AFC=2∠ABC,
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
【点评】此题考查的知识点是平行四边形的判定与性质,全等三角形的判定和性质及矩形的判定,关键是先由平行四边形的性质证三角形全等,然后推出平行四边形通过角的关系证矩形.
24.课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:
延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形或全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)问题解决:
受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(3)问题拓展:
如图3,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作∠EDF为60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
【考点】几何变换综合题.
【分析】(2)①首先延长FD到G,使得DG=DF,进而得出CF=BG,DF=DG,以及EF=EG,再利用三角形三边关系得出答案;
②由①知∠FCD=∠DBG,EF=EG,再利用勾股定理得出答案;
(3)利用全等三角形的判定与性质得出△DEG≌△DEF(SAS),进而得出EF=EG=BE+BG,即EF=BE+CF,进而得出答案.
【解答】(2)证明:①如答题图1,延长FD到G,使得DG=DF,连接BG、EG.
则CF=BG,DF=DG,
∵DE⊥DF,∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
解:②若∠A=90°,则∠EBC+∠FCB=90°,
由①知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
∴BE2+CF2=EF2;
(3)解:如答题图2,将△DCF绕点D逆时针旋转120°得到△DBG.
∵∠C+∠ABD=180°,∠4=∠C,
∴∠4+∠ABD=180°,
∴点E、B、G在同一直线上.
∵∠3=∠1,∠BDC=120°,∠EDF=60°,
∴∠1+∠2=60°,故∠2+∠3=60°,即∠EDG=60°
∴∠EDF=∠EDG=60°,
在△DEG和△DEF中,
∴△DEG≌△DEF(SAS),
∴EF=EG=BE+BG,即EF=BE+CF.
【点评】此题主要考查了几何变换综合以及全等三角形的判定与性质、勾股定理等知识,正确得出△DEG≌△DEF(SAS)是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
