第五章 相交线判定小专题精讲2 拐点型拉平行导角转化课件
文档属性
| 名称 | 第五章 相交线判定小专题精讲2 拐点型拉平行导角转化课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 135.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-15 00:00:00 | ||
图片预览



文档简介
(共14张PPT)
专题二:拐点类型 拉平行线导角转化
5.2.2 平行线的判定小专题精讲
人教版 七年级下
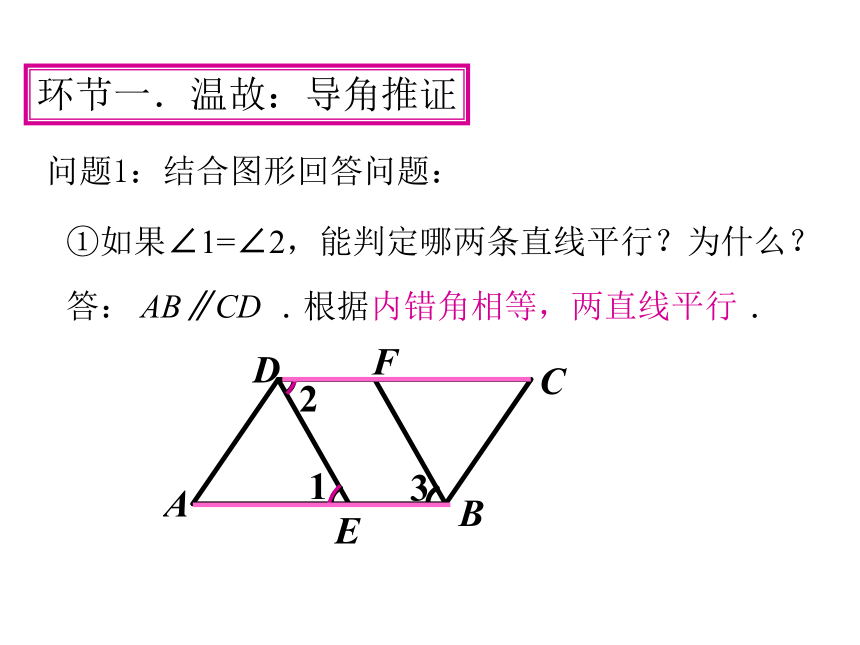
问题1:结合图形回答问题:
答: AB∥CD .根据内错角相等,两直线平行.
环节一.温故:导角推证
①如果∠1=∠2,能判定哪两条直线平行?为什么?
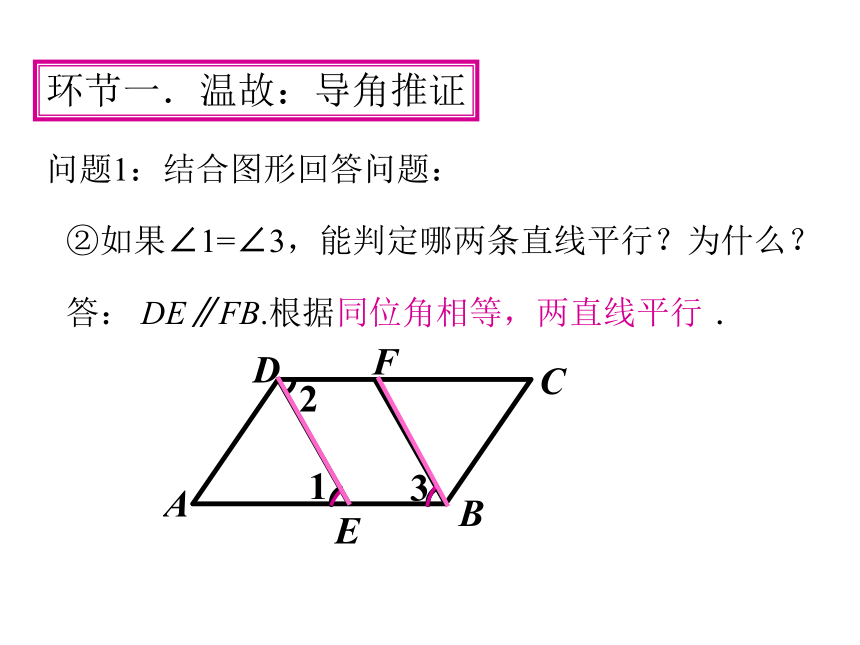
问题1:结合图形回答问题:
答: DE∥FB.根据同位角相等,两直线平行.
②如果∠1=∠3,能判定哪两条直线平行?为什么?
环节一.温故:导角推证
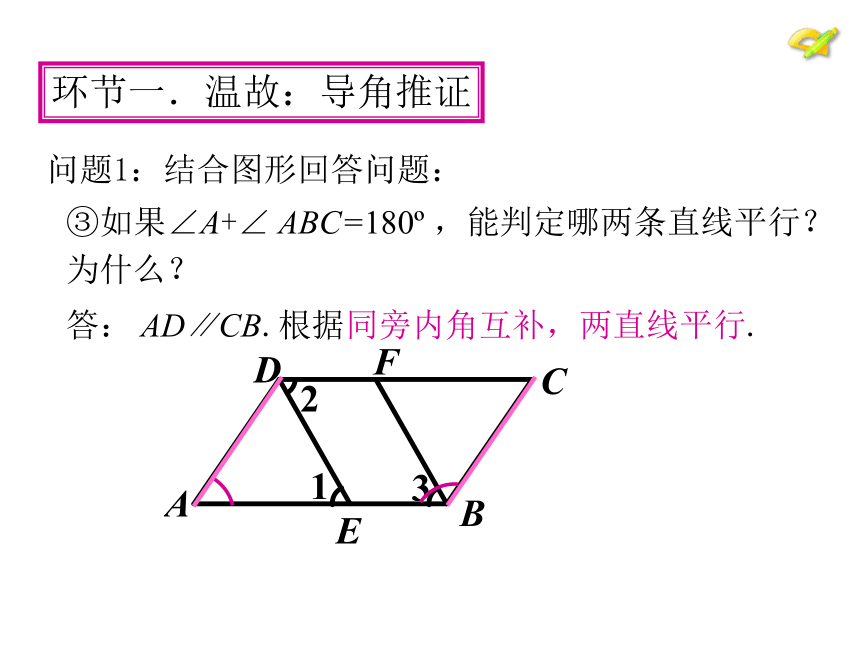
问题1:结合图形回答问题:
答: AD∥CB.根据同旁内角互补,两直线平行.
③如果∠A+∠ ABC=180 ,能判定哪两条直线平行?为什么?
环节一.温故:导角推证
问题2 如图,当∠1=∠2时,AB 与CD平行吗?
为什么?
答: AB∥CD .
理由如下:
∵ ∠1=∠2,
又∵ ∠2=∠3 ,
∴ ∠1=∠3 .
∵ ∠1和∠3是同位角 ,
∴ AB∥CD(同位角相等,两直线平行).
环节一.温故:导角推证
已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?
问题3 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
环节一.温故:导角推证
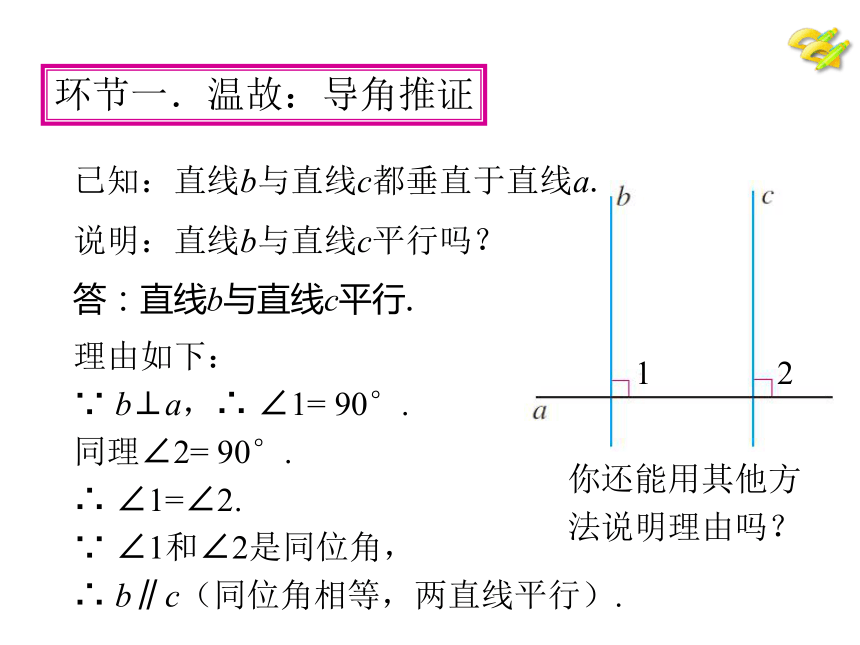
已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?
答:直线b与直线c平行.
理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).
1
2
你还能用其他方法说明理由吗?
环节一.温故:导角推证
三种思路:定义、判定、平行公理
思路一:定义法
思路二:方法1:同位角相等,两直线平行
方法2:内错角相等,两直线平行
方法3:同旁内角互补,两直线平行
思路三:依据过直线外一点有且仅有一条直线与已知直线平行,由此得到:
方法4:平行传递性:平行于同一直线两直线平行
方法5:垂直于同一直线的两直线平行
环节二.归类:证平行的五种方法
环节三:探索:拐点类型
典题1:单拐点:
如图,∠BFM=∠1+∠2,求证:AB平行CD
思路点拔:过M点能作AB的平行线有几条?由此你发现什么 ?结论:导角可证直线相互关系
环节三:探索 拐点类型拉平行
双拐点:如图:∠B=25度,∠BCD=45度,∠CDE=30度,∠E=10度,试说明AB平行于EF
点拔:依据平行公理作平行,再由平行线导角证平行,再由平行线传递性转化
环节四:巩固
变式跟进1:(2017赤峰)如图1:∠1=∠2,∠3=∠4,试探究AB与EF关系
变式跟进2:如图2,∠EAB-∠ECD=∠AEC,求证:AB平行CD
变式跟进3:(2017武汉期中)如图,直线l1平行l2,且l3和它们交于A,B两点,点P在AB上,点M,N分别在l1平行l2,∠PMA=∠1,∠PNB=∠2,∠MPN=∠3
(1)请说明∠1,∠2,∠3之间的关系并说明理由
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合
变式跟进3:(2017武汉期中)如图,直线l1平行l2,且l3和它们交于A,B两点,点P在AB上,点M,N分别在l1平行l2,∠PMA=∠1,∠PNB=∠2,∠MPN=∠3
(1)请说明∠1,∠2,∠3之间的关系并说明理由
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合
(1)平行线的判定方法有哪些?
环节五:小结
(2)结合例题,能用自己的语言说一说解决与平行线的判定有关的问题的思路吗?
专题二:拐点类型 拉平行线导角转化
5.2.2 平行线的判定小专题精讲
人教版 七年级下
问题1:结合图形回答问题:
答: AB∥CD .根据内错角相等,两直线平行.
环节一.温故:导角推证
①如果∠1=∠2,能判定哪两条直线平行?为什么?
问题1:结合图形回答问题:
答: DE∥FB.根据同位角相等,两直线平行.
②如果∠1=∠3,能判定哪两条直线平行?为什么?
环节一.温故:导角推证
问题1:结合图形回答问题:
答: AD∥CB.根据同旁内角互补,两直线平行.
③如果∠A+∠ ABC=180 ,能判定哪两条直线平行?为什么?
环节一.温故:导角推证
问题2 如图,当∠1=∠2时,AB 与CD平行吗?
为什么?
答: AB∥CD .
理由如下:
∵ ∠1=∠2,
又∵ ∠2=∠3 ,
∴ ∠1=∠3 .
∵ ∠1和∠3是同位角 ,
∴ AB∥CD(同位角相等,两直线平行).
环节一.温故:导角推证
已知条件:直线b与直线c都垂直于直线a.
要说明的结论:直线b与直线c平行吗?
问题3 在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
环节一.温故:导角推证
已知:直线b与直线c都垂直于直线a.
说明:直线b与直线c平行吗?
答:直线b与直线c平行.
理由如下:
∵ b⊥a,∴ ∠1= 90°.
同理∠2= 90°.
∴ ∠1=∠2.
∵ ∠1和∠2是同位角,
∴ b∥c(同位角相等,两直线平行).
1
2
你还能用其他方法说明理由吗?
环节一.温故:导角推证
三种思路:定义、判定、平行公理
思路一:定义法
思路二:方法1:同位角相等,两直线平行
方法2:内错角相等,两直线平行
方法3:同旁内角互补,两直线平行
思路三:依据过直线外一点有且仅有一条直线与已知直线平行,由此得到:
方法4:平行传递性:平行于同一直线两直线平行
方法5:垂直于同一直线的两直线平行
环节二.归类:证平行的五种方法
环节三:探索:拐点类型
典题1:单拐点:
如图,∠BFM=∠1+∠2,求证:AB平行CD
思路点拔:过M点能作AB的平行线有几条?由此你发现什么 ?结论:导角可证直线相互关系
环节三:探索 拐点类型拉平行
双拐点:如图:∠B=25度,∠BCD=45度,∠CDE=30度,∠E=10度,试说明AB平行于EF
点拔:依据平行公理作平行,再由平行线导角证平行,再由平行线传递性转化
环节四:巩固
变式跟进1:(2017赤峰)如图1:∠1=∠2,∠3=∠4,试探究AB与EF关系
变式跟进2:如图2,∠EAB-∠ECD=∠AEC,求证:AB平行CD
变式跟进3:(2017武汉期中)如图,直线l1平行l2,且l3和它们交于A,B两点,点P在AB上,点M,N分别在l1平行l2,∠PMA=∠1,∠PNB=∠2,∠MPN=∠3
(1)请说明∠1,∠2,∠3之间的关系并说明理由
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合
变式跟进3:(2017武汉期中)如图,直线l1平行l2,且l3和它们交于A,B两点,点P在AB上,点M,N分别在l1平行l2,∠PMA=∠1,∠PNB=∠2,∠MPN=∠3
(1)请说明∠1,∠2,∠3之间的关系并说明理由
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合
(1)平行线的判定方法有哪些?
环节五:小结
(2)结合例题,能用自己的语言说一说解决与平行线的判定有关的问题的思路吗?
