陕西省黄陵中学2017-2018学年高二(重点班)下学期开学考试数学(理)试题
文档属性
| 名称 | 陕西省黄陵中学2017-2018学年高二(重点班)下学期开学考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 358.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-13 21:36:35 | ||
图片预览



文档简介
高二重点班开学考试数学试题(理)
第Ⅰ卷(共60分)
第I卷(选择题60分)
选择题(本大题共12个小题,每小题5分,共60分。)
1.在数列1,2,,,,…中,是这个数列的第( )
A. 16项 B. 24项 C. 26项 D. 28项
2.在中,若则的形状一定是()
A. 等腰直角三角形 B. 等腰三角形
C. 直角三角形 D. 等边三角形
3.直线过点且与抛物线只有一个公共点,这样的直线共有( )
A.条 B.条 C.条 D.条
4.右图是抛物线形拱桥,当水面在位置时,拱顶离水面2米,水面宽4米,则水位下降2米后(水足够深),水面宽( )米
A. B. C. D.
5.已知枚的一元硬币中混有枚五角硬币,从中任意取出两枚,已知其中一枚为五角硬币,则两枚都是五角硬币的概率为( )
A. B. C. D.
6.将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由落下,小球在下落过程中,将次遇到黑色障碍物,最后落入袋或袋中,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率分别为、,则小球落入袋中的概率为( )
A. B. C. D.
7.已知变量,满足约束条件,若目标函数的最小值为,则( )
A. B. C. D.
8.设为坐标原点,动点在圆:上,过作轴的垂线,垂足为,点满足,则点的轨迹方程为( )
A. B. C. D.
9.若,为互斥事件,则( )
A. B.
C. D.
10.如图是函数的导函数的图象,给出下列命题:
①-2是函数的极值点;
②1是函数的极值点;
③的图象在处切线的斜率小于零;
④函数在区间上单调递增.
则正确命题的序号是( )
A.①③ B.②④ C.②③ D. ①④
11.已知点为双曲线的右支上一点,,为双曲线的左、右焦点,若(为坐标原点),且,则双曲线的离心率为( )
A. B. C. D.
12.设奇函数在上存在导函数,且在上,若,则实数的取值范围为( )
A. B.
C. D.
二、填空题:(本大题共4小题,每小题5分,共20分,将答案填在答题纸的横线上)
13、的展开式中的系数为70,则=________.
14、在区间上随机取一个数x,的值介于的概率为 .
15、从4名男生和2名女生中任选3人参加演讲比赛,设随机变量X表示所选3人中女生
的人数,则P(X≤1)等于 .
16、已知,则= .
三、解答题(本大题共6小题,共70分。请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。)
解答题:解答应写出文字说明、证明过程或验算步骤,共70分
17.(本小题满分10分)
已知命题表示焦点在轴上的椭圆;命题双曲线的离心率.若命题为真命题,为假命题,求的取值范围.
18.(本小题满分12分)
在中,内角的对边分别为,已知.
(1)求的值;(2)若为钝角,,求的取值范围。
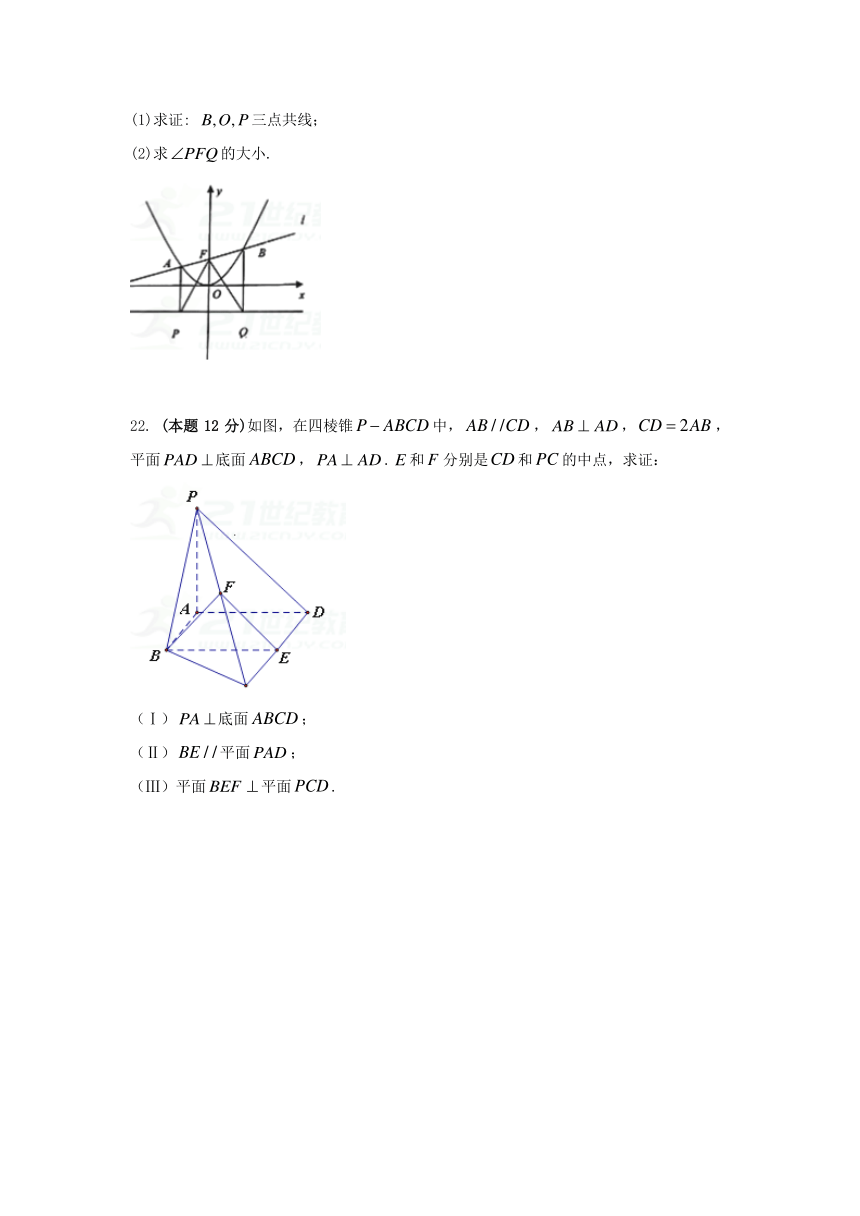
21. (本题12分)如图,已知抛物线的焦点为,过的直线交抛物线于两点,过作准线的垂线,垂足为为原点.
(1)求证: 三点共线;
(2)求的大小.
22. (本题12分)如图,在四棱锥中,,,,平面底面,.和分别是和的中点,求证:
(Ⅰ)底面;
(Ⅱ)平面;
(Ⅲ)平面平面.
1-4.CBCB 5-8.DDCB 9-12.BDBD
13、±1 14、 15、 16、180
(10分)解:若真,则,解得:.
若真,则且,解得:.
为真命题,为假命题
,中有且只有一个为真命题,即必一真一假
① 若真假,则 即
② 若假真,则 即
实数的取值范围为:
(12分)解:(1)由正弦定理:设,
则
即
化简得:
即,又
即
由(1)及正弦定理知,即
由题意:解之得:
则的取值范围是
19、(12分)
证: ;
;
.
由此推测:.(*)
下面用数学归纳法证明(*)式.
(i)当时,左边=右边=2,(*)式成立.
(ii)假设当时(*)式成立,即 .
那么当时,,由归纳假设可得
.
当时,(*)式也成立.
根据(i)(ii),可知(*)式对一切正整数都成立.
(2)证:①当时,左边=,不等式成立.
②假设当时不等式成立,即 .
则当时,
(12分)
解:(1)在四面体中任取一点,连接并延长交对面于点,则.
证明:在四面体与中,
同理有:
(2)法一:假设均成立,
则三式相乘,得 ①
由于,
同理:.
三式相乘,得 ②
②与①矛盾,故假设不成立.
不都大于1.
方法二:假设均成立.
③
而 ④
④与③矛盾,故假设不成立.
原题设结论成立
21.
(1)设直线
由消去y整理得
设
则
因为
所以,
所以,
又线段有公共点,
所以三点共线.
(2)因为
所以,
所以,
所以
22.
(Ⅰ)因为平面底面,且垂直于这两个平面的交线,
所以底面.
(Ⅱ)因为,,是的中点,
所以,且.
所以为平行四边形.
所以,.
又因为平面,平面,
所以平面.
(Ⅲ)因为,并且为平行四边形,
所以,.
由(Ⅰ)知底面,
所以,
所以平面.
所以.
因为和分别是和的中点,
所以.
所以.
所以平面.
所以平面平面.
第Ⅰ卷(共60分)
第I卷(选择题60分)
选择题(本大题共12个小题,每小题5分,共60分。)
1.在数列1,2,,,,…中,是这个数列的第( )
A. 16项 B. 24项 C. 26项 D. 28项
2.在中,若则的形状一定是()
A. 等腰直角三角形 B. 等腰三角形
C. 直角三角形 D. 等边三角形
3.直线过点且与抛物线只有一个公共点,这样的直线共有( )
A.条 B.条 C.条 D.条
4.右图是抛物线形拱桥,当水面在位置时,拱顶离水面2米,水面宽4米,则水位下降2米后(水足够深),水面宽( )米
A. B. C. D.
5.已知枚的一元硬币中混有枚五角硬币,从中任意取出两枚,已知其中一枚为五角硬币,则两枚都是五角硬币的概率为( )
A. B. C. D.
6.将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由落下,小球在下落过程中,将次遇到黑色障碍物,最后落入袋或袋中,已知小球每次遇到黑色障碍物时,向左、右两边下落的概率分别为、,则小球落入袋中的概率为( )
A. B. C. D.
7.已知变量,满足约束条件,若目标函数的最小值为,则( )
A. B. C. D.
8.设为坐标原点,动点在圆:上,过作轴的垂线,垂足为,点满足,则点的轨迹方程为( )
A. B. C. D.
9.若,为互斥事件,则( )
A. B.
C. D.
10.如图是函数的导函数的图象,给出下列命题:
①-2是函数的极值点;
②1是函数的极值点;
③的图象在处切线的斜率小于零;
④函数在区间上单调递增.
则正确命题的序号是( )
A.①③ B.②④ C.②③ D. ①④
11.已知点为双曲线的右支上一点,,为双曲线的左、右焦点,若(为坐标原点),且,则双曲线的离心率为( )
A. B. C. D.
12.设奇函数在上存在导函数,且在上,若,则实数的取值范围为( )
A. B.
C. D.
二、填空题:(本大题共4小题,每小题5分,共20分,将答案填在答题纸的横线上)
13、的展开式中的系数为70,则=________.
14、在区间上随机取一个数x,的值介于的概率为 .
15、从4名男生和2名女生中任选3人参加演讲比赛,设随机变量X表示所选3人中女生
的人数,则P(X≤1)等于 .
16、已知,则= .
三、解答题(本大题共6小题,共70分。请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。)
解答题:解答应写出文字说明、证明过程或验算步骤,共70分
17.(本小题满分10分)
已知命题表示焦点在轴上的椭圆;命题双曲线的离心率.若命题为真命题,为假命题,求的取值范围.
18.(本小题满分12分)
在中,内角的对边分别为,已知.
(1)求的值;(2)若为钝角,,求的取值范围。
21. (本题12分)如图,已知抛物线的焦点为,过的直线交抛物线于两点,过作准线的垂线,垂足为为原点.
(1)求证: 三点共线;
(2)求的大小.
22. (本题12分)如图,在四棱锥中,,,,平面底面,.和分别是和的中点,求证:
(Ⅰ)底面;
(Ⅱ)平面;
(Ⅲ)平面平面.
1-4.CBCB 5-8.DDCB 9-12.BDBD
13、±1 14、 15、 16、180
(10分)解:若真,则,解得:.
若真,则且,解得:.
为真命题,为假命题
,中有且只有一个为真命题,即必一真一假
① 若真假,则 即
② 若假真,则 即
实数的取值范围为:
(12分)解:(1)由正弦定理:设,
则
即
化简得:
即,又
即
由(1)及正弦定理知,即
由题意:解之得:
则的取值范围是
19、(12分)
证: ;
;
.
由此推测:.(*)
下面用数学归纳法证明(*)式.
(i)当时,左边=右边=2,(*)式成立.
(ii)假设当时(*)式成立,即 .
那么当时,,由归纳假设可得
.
当时,(*)式也成立.
根据(i)(ii),可知(*)式对一切正整数都成立.
(2)证:①当时,左边=,不等式成立.
②假设当时不等式成立,即 .
则当时,
(12分)
解:(1)在四面体中任取一点,连接并延长交对面于点,则.
证明:在四面体与中,
同理有:
(2)法一:假设均成立,
则三式相乘,得 ①
由于,
同理:.
三式相乘,得 ②
②与①矛盾,故假设不成立.
不都大于1.
方法二:假设均成立.
③
而 ④
④与③矛盾,故假设不成立.
原题设结论成立
21.
(1)设直线
由消去y整理得
设
则
因为
所以,
所以,
又线段有公共点,
所以三点共线.
(2)因为
所以,
所以,
所以
22.
(Ⅰ)因为平面底面,且垂直于这两个平面的交线,
所以底面.
(Ⅱ)因为,,是的中点,
所以,且.
所以为平行四边形.
所以,.
又因为平面,平面,
所以平面.
(Ⅲ)因为,并且为平行四边形,
所以,.
由(Ⅰ)知底面,
所以,
所以平面.
所以.
因为和分别是和的中点,
所以.
所以.
所以平面.
所以平面平面.
同课章节目录
