数学六年级上人教版第8单元 数学广角——数与形课(23张)
文档属性
| 名称 | 数学六年级上人教版第8单元 数学广角——数与形课(23张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-03-14 11:09:05 | ||
图片预览







文档简介
(共23张PPT)
8 数学广角——数与形
1.
结合上面的图形填一填。
(1) 1 =12
1+3=( )2
1+3+5=( )2
2
3
(2)三个等式的左边是从“1”开始,连续的( )相加,等于奇数的
个数的( )。
(3)1+3+5+7=( )2
奇数
平方
4
2.计算
(1)这个算式是从 加起,后面的一个数依次是前一个数的( ),并
且加数的个数是( )。
无限的
(2)结合线段图或圆形图,可以发现:这些数无限地加下去的和是
( )。
1
1.请你填一填。
(1)按如图规律,第8堆有( )个○。
64
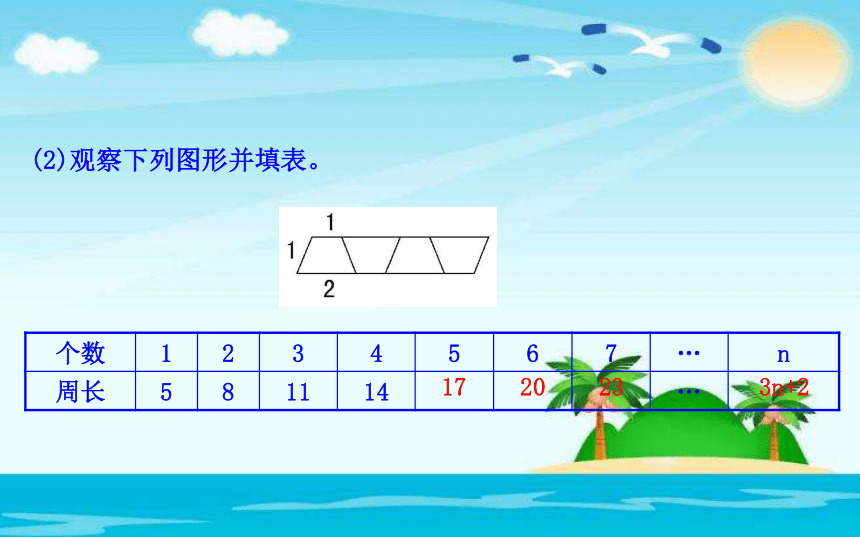
(2)观察下列图形并填表。
个数 1 2 3 4 5 6 7 … n
周长 5 8 11 14 …
17
20
23
3n+2
2.请你选一选。
(1)如图,图案是由边长为单位长度的小正方形按一定的规律拼接而
成。依此规律,第6个图案中小正方形的个数为( )。
A.21 B.29 C.41 D.61
D
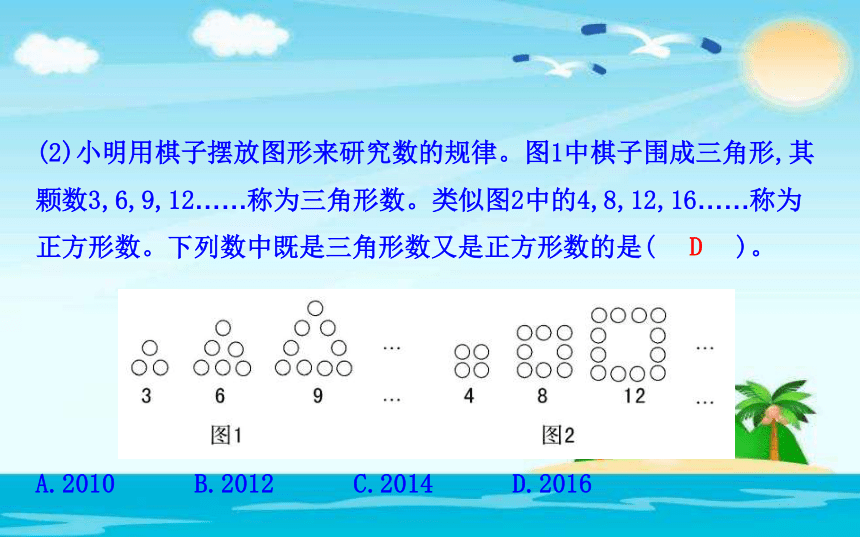
(2)小明用棋子摆放图形来研究数的规律。图1中棋子围成三角形,其
颗数3,6,9,12……称为三角形数。类似图2中的4,8,12,16……称为
正方形数。下列数中既是三角形数又是正方形数的是( )。
A.2010 B.2012 C.2014 D.2016
D
3.每边坐一人的方桌,2张拼起来可坐6人,3张、4张、5张……拼起来,各可坐多少人 如图:
仔细观察并填写下表:
由图可知,每多拼一张桌子,可多坐( )人。
200
…
…
18
…
…
4
3
6
2
4
1
可坐人数
桌子数
8
10
38
99
2
4.你做过手指记数的游戏吗 一个小朋友按如图所示的规则练习记数,
当他数到25时,对应的是( )指;数到107时,对应的是( )
指。根据你发现的规律,数到2008时,对应的是( )指。(填出指
头的名称,各指头的名称从上到下依次为大拇指、食指、中指、无名
指、小指)
大拇
中
食
5.观察如下图所示五角形数,填一填。
(1)如果第一个数的算式是1=1,第二个数的算式是5=1+4,那么
第三个数的算式是( ),第五个数的算式是
( )。
(2)第10个数的算式是( )。
(3)第50个数的算式是( )。
12=1+4+7
35=1+4+7+10+13
145=1+4+7+10+13+16+19+22+25+28
3725=1+4+7+10+…+145+148
6.完成下表,并解答问题。
多边形 …
边数 3 4 5 6 …
内角和 180° 360° 540° 720° …
(1)10边形的内角和是( )。
(2)100边形的内角和是( )。
1440°
17640°
(3)你有什么发现
多边形的内角和等于边数与2的差再乘180°。
计算公式是(n-2)×180°。
7.有一个正方形,通过多次划分,得到若干个正方形,具体操作如下:
第1次把它等分成4个小正方形,第2次将上次分成小正方形的其中一个又等分成4个小正方形……依此操作下去。
(1)通过观察和猜想,将第3次、第4次和第n次划分图中得到的正方形总个数填入表中。
次数 第1次 第2次 第3次 第4次 … 第n次
正方形
总个数 …
5
9
13
17
4n+1
(2)请你推断,按上述操作方法,能否得到103个正方形 为什么
不能。因为第n次划分后,图中共有(4n+1)个正方形,所以可得4n+1=103,则n=25.5,方程没有整数解,所以不能得到103个正方形。
【题目】观察下面由点组成的图形,请回答:
1.第十个图形中有多少个点
2.第n个图形中有多少个点
【分析】1.观察图形可知:前四个图形中包含的点数分别是:1,4,7,10。可见,在每相邻的两个数中,后一个数都比前一个数大3。由此可用列表法得到第10个图形中点的个数。
2.第二个图形是3+1=4;第三个图形是3+3+1=7。可知图形中点的个数是3(n-1)+1。
【解答】1.
答:第十个图形中有28个点。
2.3(n-1)+1 答:第n个图形中有3(n-1)+1个点。
第几个 1 2 3 4 5 6 7 8 9 10
点数 1 4 7 10 13 16 19 22 25 28
8 数学广角——数与形
1.
结合上面的图形填一填。
(1) 1 =12
1+3=( )2
1+3+5=( )2
2
3
(2)三个等式的左边是从“1”开始,连续的( )相加,等于奇数的
个数的( )。
(3)1+3+5+7=( )2
奇数
平方
4
2.计算
(1)这个算式是从 加起,后面的一个数依次是前一个数的( ),并
且加数的个数是( )。
无限的
(2)结合线段图或圆形图,可以发现:这些数无限地加下去的和是
( )。
1
1.请你填一填。
(1)按如图规律,第8堆有( )个○。
64
(2)观察下列图形并填表。
个数 1 2 3 4 5 6 7 … n
周长 5 8 11 14 …
17
20
23
3n+2
2.请你选一选。
(1)如图,图案是由边长为单位长度的小正方形按一定的规律拼接而
成。依此规律,第6个图案中小正方形的个数为( )。
A.21 B.29 C.41 D.61
D
(2)小明用棋子摆放图形来研究数的规律。图1中棋子围成三角形,其
颗数3,6,9,12……称为三角形数。类似图2中的4,8,12,16……称为
正方形数。下列数中既是三角形数又是正方形数的是( )。
A.2010 B.2012 C.2014 D.2016
D
3.每边坐一人的方桌,2张拼起来可坐6人,3张、4张、5张……拼起来,各可坐多少人 如图:
仔细观察并填写下表:
由图可知,每多拼一张桌子,可多坐( )人。
200
…
…
18
…
…
4
3
6
2
4
1
可坐人数
桌子数
8
10
38
99
2
4.你做过手指记数的游戏吗 一个小朋友按如图所示的规则练习记数,
当他数到25时,对应的是( )指;数到107时,对应的是( )
指。根据你发现的规律,数到2008时,对应的是( )指。(填出指
头的名称,各指头的名称从上到下依次为大拇指、食指、中指、无名
指、小指)
大拇
中
食
5.观察如下图所示五角形数,填一填。
(1)如果第一个数的算式是1=1,第二个数的算式是5=1+4,那么
第三个数的算式是( ),第五个数的算式是
( )。
(2)第10个数的算式是( )。
(3)第50个数的算式是( )。
12=1+4+7
35=1+4+7+10+13
145=1+4+7+10+13+16+19+22+25+28
3725=1+4+7+10+…+145+148
6.完成下表,并解答问题。
多边形 …
边数 3 4 5 6 …
内角和 180° 360° 540° 720° …
(1)10边形的内角和是( )。
(2)100边形的内角和是( )。
1440°
17640°
(3)你有什么发现
多边形的内角和等于边数与2的差再乘180°。
计算公式是(n-2)×180°。
7.有一个正方形,通过多次划分,得到若干个正方形,具体操作如下:
第1次把它等分成4个小正方形,第2次将上次分成小正方形的其中一个又等分成4个小正方形……依此操作下去。
(1)通过观察和猜想,将第3次、第4次和第n次划分图中得到的正方形总个数填入表中。
次数 第1次 第2次 第3次 第4次 … 第n次
正方形
总个数 …
5
9
13
17
4n+1
(2)请你推断,按上述操作方法,能否得到103个正方形 为什么
不能。因为第n次划分后,图中共有(4n+1)个正方形,所以可得4n+1=103,则n=25.5,方程没有整数解,所以不能得到103个正方形。
【题目】观察下面由点组成的图形,请回答:
1.第十个图形中有多少个点
2.第n个图形中有多少个点
【分析】1.观察图形可知:前四个图形中包含的点数分别是:1,4,7,10。可见,在每相邻的两个数中,后一个数都比前一个数大3。由此可用列表法得到第10个图形中点的个数。
2.第二个图形是3+1=4;第三个图形是3+3+1=7。可知图形中点的个数是3(n-1)+1。
【解答】1.
答:第十个图形中有28个点。
2.3(n-1)+1 答:第n个图形中有3(n-1)+1个点。
第几个 1 2 3 4 5 6 7 8 9 10
点数 1 4 7 10 13 16 19 22 25 28
