18.2 勾股定理的逆定理同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
18.2 勾股定理的逆定理同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
(1)勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
说明:
①勾股定理的逆定理验证利用了三角形的全等.
②勾股定理的逆定理将数转化为形,作用是判断一个三角形是不是直角三角形.必须满足较小两边平方的和等于最大边的平方才能做出判断.
(2)运用勾股定理的逆定理解决问题的实质就是判断一个角是不是直角.然后进一步结合其他已知条件来解决问题.
注意:要判断一个角是不是直角,先要构造出三角形,然后知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
基础知识和能力拓展精练
一、选择题
1.以下列各组数为边长,能构成直角三角形的是( )
A. 4,5,6 B. 1,1, C. 6,8,11 D. 5,12,23
2.已知a,b,c是三角形的三边长,如果满足(a-6)2++=0,那么下列说法中不正确的是( )
A. 这个三角形是直角三角形 B. 这个三角形的最长边长是10
C. 这个三角形的面积是48 D. 这个三角形的最长边上的高是4.8
3.若a,b,C是△ABC的三条边,且满足a2﹣2ab+b2=0,(a+b)2=2ab+c2, 则△ABC的形状为( )
A. 直角三角形 B. 等腰三角形 C. 等边三角形 D. 等腰直角三角形
4.在平面直角坐标系中,点A(0,-1),点B(4,2),点C在坐标轴上,使∠ACB为直角的点C有( )个
A. 1 B. 2 C. 3 D. 4
5.如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A、B、C恰好在网格图中的格点上,那么△ABC中BC边上的高是( )
A. B. C. D.
6.如图,在由单位正方形组成的网格图标中有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的线段是( )
A. AB,CD,EF B. AB,CD,GH C. AB,EF,GH D. CD,EF,GH
7.小华和小刚兄弟两个同时从家去同一所学校上学,速度都是每分钟走50米.小华从家到学校走直线用了10分钟,而小刚从家出发先去找小明再到学校(均走直线),小刚到小明家用了6分钟,小明家到学校用了8分钟,小刚上学走了个( )
A. 锐角弯 B. 钝角弯 C. 直角弯 D. 不能确定
8.甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°
二、填空题
9.如图,平行四边形ABCD中,AC=4cm,BC=5cm,CD=3cm,则 ABCD的面积________.
10.把一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,则这个三角形是_______三角形.
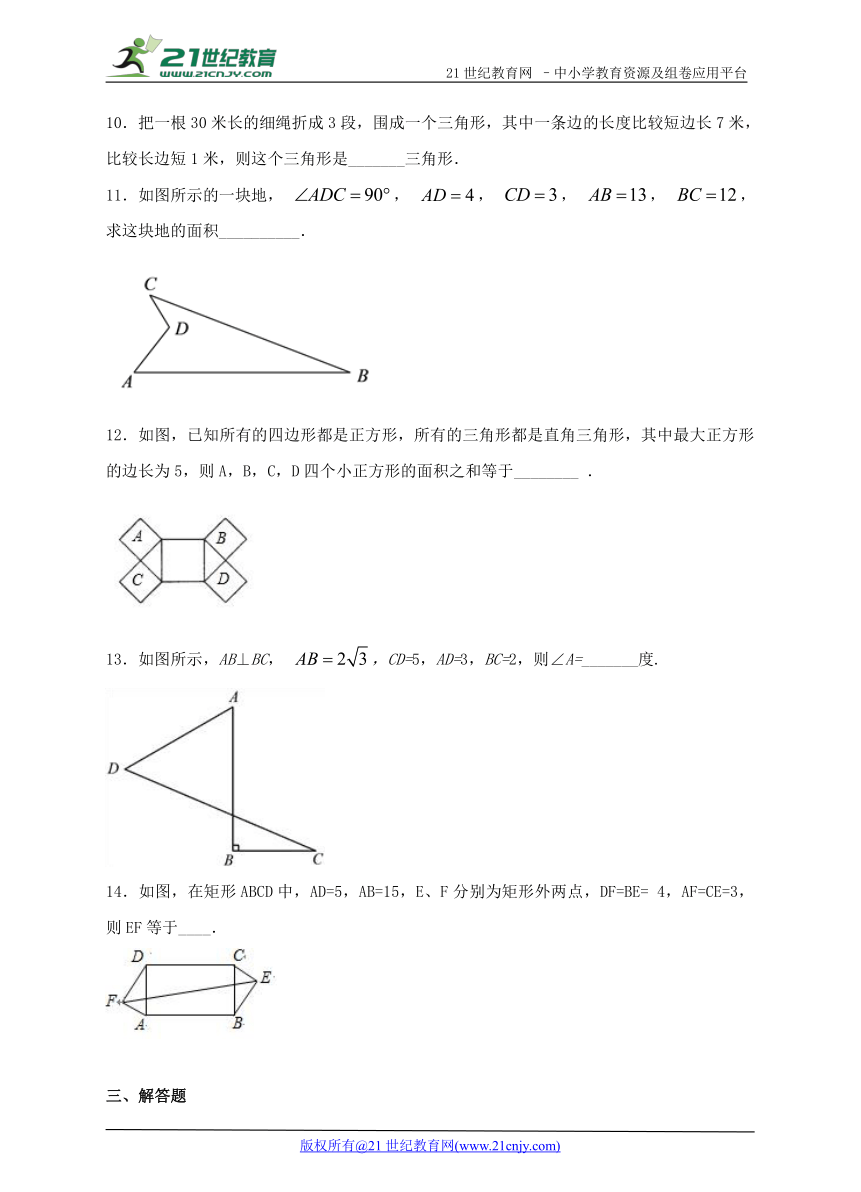
11.如图所示的一块地, , , , , ,求这块地的面积__________.
12.如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5,则A,B,C,D四个小正方形的面积之和等于________ .
13.如图所示,AB⊥BC, ,CD=5,AD=3,BC=2,则∠A=_______度.
14.如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE= 4,AF=CE=3,则EF等于____.
三、解答题
15.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.
16.如图,已知正方形ABCD的边长为4,E为AB中点,F为AD上的一点,且AF=AD,试判断△EFC的形状.
17.龙梅和玉荣是草原上的好朋友,可是有一次经过一场争吵之后,两人不欢而散,龙梅的速度是米/秒,4分钟后她停了下来,觉得有点后悔了,玉荣走的方向好像是和龙梅成直角,她的速度是米/秒,如果她和龙梅同时停下来,而这时候她俩正好相距200米,那么她走的方向是否成直角?如果她们现在想讲和,那么原来的速度相向而行,多长时间后能相遇?
18.如图所示,在四边形ABCD中,AB=2,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
19.如图,甲、乙两船从港口A同时出发,甲船以30海里/时的速度向北偏东35°的方向航行,乙船以40海里/时的速度向另一方向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,则乙船航行的方向是南偏东多少度?
20.已知:如图,AB=4,BC=12,CD=13,DA=3,AB⊥AD.
求证:BC⊥BD.
21.如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?
参考答案
1.B
【解析】选项B, ,满足勾股定理逆定理,A,C,D,不满足,故选B.
2.C
【解析】试题解析:∵(a-6)2≥0, +≥0,|c-10|≥0,(a-b)2++|c-10|=0,
∴a-6=0,b-8=0,c-10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴这个三角形是直角三角形,最长边为10,
∵6×8÷2=24,
∴这个三角形面积为24,
∵24×2÷10=4.8.
∴这个三角形最长边上的高为4.8.
故选C.
3.D
【解析】试题解析:
∴a b=0,即a=b,
∴△ABC为等腰三角形;
又
∴△ABC也是直角三角形;
∴△ABC为等腰直角三角形.
故选D.
点睛:如果一个三角形两边的平方和等于第三条边的平方,那么这个三角形是直角三角形.
4.C
【解析】试题解析:当C在x轴上时,有∠ACB=90°,此时C(4,0);
当C在y轴上时,设C(0,y),假设∠ACB=90°,则有:AC2+BC2=AB2.
∴1+y2+42+(2-y)2=52+22
整理得:y2-2y-4=0
解得: ,
∴点C的坐标为:(0, ),(0, )
故点C有三个.
故选C.
5.A
【解析】先用勾股定理耱出三角形的三边,再根据勾股定理的逆定理判断出△ABC是直角三角形,最后设BC边上的高为h,利用三角形面积公式建立方程即可得出答案.
解:由勾股定理得:
, , ,
,即
∴△ABC是直角三角形,
设BC边上的高为h,
则,
∴.
故选A.
点睛:本题主要考查勾股理及其逆定理.借助网格利用勾股定理求边长,并用勾股定理的逆定理来判断三角形是否是直角三角形是解题的关键.
6.C
【解析】由勾股定理知,EF=,AB=,CD=, ,
5+8=13, ,所以由勾股定理逆定理AB,EF,GH可以构成直角三角形.
所以选C.
点睛:
勾股定理:在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方.这个定理叫毕达哥拉斯定理,最早由毕达哥拉斯证明,中国商代发现了勾三股四弦五,仅仅是一个特例,严格讲不能叫定理.
设直角三角形两直角边为a和b,斜边为c,有 a2 + b2 = c2 .
勾股定理逆定理:如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.最长边所对的角为直角.
设三角形三边有 a2 + b2 = c2 . 则∠C=90°.
7.C
【解析】试题解析:∵小华从家到学校走直线用了10分钟,速度是每分钟走50米,
∴小华家到学校的直线距离=50×10=500(米);
∵小刚到小明家用了6分钟,
∴小刚到小明家的距离=50×6=300(米);
∵小明家到学校用了8分钟,
∴小明家到学校的距离=50×8=400(米).
∵3002+4002=5002,
∴小刚上学走了个直角弯.
故选C.
8.C
【解析】如图,根据题意得OA=40×15=600,OB=40×20=800,
因为6002=360000,8002=640000,10002=1000000,360000+640000=1000000.
所以6002+8002=10002.
所以∠AOB=∠AOB=90°,所以∠BOS=∠B′ON=60°,所以乙客轮的航行方向可能是南偏东60°或北偏西60°.
故选C.
9.12cm2
【解析】 ∵四边形ABCD是平行四边形,
∴AB=CD=3cm,
∵AC=4cm,BC=5cm,
∴AC2+AB2=AC2,
∴△ABC是直角三角形,
∴S△ABC=×3×4=6cm2,
∴则ABCD的面积=2×6=12cm2.
10.直角
【解析】试题解析:设中间长的边长为x,较长边为x+1,较短边为x-7,
∵此三角形周长为30米,
∴x+x+1+x-7=30,
解得:x=12,
则x+1=13,x-7=5,
∵52+122=132,
∴这个三角形的形状为直角三角形.
故答案为:直角.
11.
【解析】连接,
∵, , .
∴
.
∵.
∴.
∴.
∴
.
12.50
【解析】试题解析:∵所有的三角形都是直角三角形,
∴正方形A和C的面积和就是大正方形的面积,
同理,正方形B和D的面积和等于大正方形的面积,
∴四个小正方形的面积=2×5×5=50.
故答案为:50.
13.60
【解析】解:连接AC,∵AB⊥BC,∴AC===4,∴∠BAC=30°.
∵==25= ,∴∠DAC=90°,∴∠DAB=90°-30°=60°.故答案为:60.
14.
【解析】由题意得: 都是直角三角形.
,
15.见解析
【解析】试题分析:移项,配成三个完全平方;三个非负数的和为0,则都为0;已知a、b、c,利用勾股定理的逆定理判断三角形的形状为直角三角形.
试题解析:解:由已知可得a2-10a+25+b2-24b+144+c2-26c+169=0,
配方并化简得,(a-5)2+(b-12)2+(c-13)2=0.
∵(a-5)2≥0,(b-12)2≥0,(c-13)2≥0.
∴a-5=0,b-12=0,c-13=0.
解得a=5,b=12,c=13.
又∵a2+b2=169=c2,
∴△ABC是直角三角形.
16.见解析
【解析】试题分析:分别计算EF、CE、CF的长度,再利用勾股定理的逆定理判断即可.
试题解析:解:∵E为AB中点,∴BE=2.
∴CE2=BE2+BC2=22+42=20.
同理可求得,EF2=AE2+AF2=22+12=5,CF2=DF2+CD2=32+42=25.
∵CE2+EF2=CF2,
∴△EFC是以∠CEF为直角的直角三角形.
点睛:(1)勾股定理
直角三角形的两条直角边的平方和等于斜边的平方.这就是勾股定理.
(2)勾股定理逆定理
在一个三角形中,两条边的平方和等于另一条边的平方,那么这个三角形就是直角三角形. 这就是勾股定理的逆定理.
17.她们走的方向成直角,如果她们想讲和,按原来的速度相向而行,171秒后能相遇.
【解析】试题分析:首先分别计算出龙梅和玉荣走的路程,进而计算得出她们走的路程长度、她们之间的距离满足勾股定理,所以她们走的方向成直角,要计算她们相遇的时间,用总路程除以她们的速度和即可.
试题解析:
龙梅走的路程: ×4×60=120(米),
玉荣走的路程: ×4×60=160(米),
∵1202+1602=2002,
∴她们走的方向成直角,
以原来的速度相向而行相遇的时间:200÷(+)=200÷ = =171(秒);
答:她们走的方向成直角,如果她们想讲和,按原来的速度相向而行,171秒后能相遇.
点睛:本题关键在于勾股定理逆定理的运用.
18.四边形ABCD的面积是6.
【解析】试题分析:连接BD,根据勾股定理可计算出BD的长度,再由勾股定理逆定理可判断出△ABD为直角三角形,分别计算出△ABD和△BCD的面积,求和即可.
试题解析:
连接BD,
∵∠C=90°,
∴△BCD为直角三角形,
∴BD2=BC2+CD2=22+12=()2,BD>0,
∴BD=,
在△ABD中,
∵AB2+BD2=20+5=25,AD2=52=25,
∴AB2+BD2=AD2,
∴△ABD为直角三角形,且∠ABD=90°,
∴S四边形ABCD=S△ABD+S△BCD=×2×+×2×1=6.
∴四边形ABCD的面积是6.
点睛:本题关键在于利用勾股定理逆定理判定出直角三角形,从而求出三角形的面积.
19.乙船航行的方向为南偏东55°.
【解析】试题分析:
由题意可知:在△ABC中,AC=60,AB=80,BC=100,由此可由“勾股定理逆定理”证得∠BAC=90°,结合∠EAD=180°和∠EAC=35°即可求得∠DAB的度数,从而得到乙船的航行方向.
试题解析:
由题意可知,在△ABC中,AC=30×2=60,AB=40×2=80,BC=100,
∴AC2=3600,AB2=6400,BC2=10000,
∴AC2+AB2=BC2,
∴∠CAB=90°,
又∵∠EAD=180°,∠EAC=35°,
∴∠DAB=90°-∠CAE=90°-35°=55°,
∴乙船航行的方向为南偏东55°.
点睛:本题的解题要点是:在△ABC中,由已知条件先求得AC和AB的长,再结合AC=100,即可用“勾股定理的逆定理”证得∠BAC=90°,这样即可求出∠DAB的度数,从而使问题得到解决.
20.见解析
【解析】试题分析:欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
试题解析: ,
在中, ,
在中,
,
.
21.3h.
【解析】试题分析:首先根据勾股定理逆定可证明△ABC是直角三角形,然后计算出∠BCD的度数,再根据直角三角形的性质算出DC的长,然后根据速度和路程可计算出多长时间后这人距离B送奶站最近.
试题解析:解:过B作BD⊥公路于D.∵82+152=172,∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°.
∵∠1=30°,∴∠BCD=180°-90°-30°=60°.
在Rt△BCD中,∵∠BCD=60°,∴∠CBD=30°,∴CD=BC=×15=7.5(km).
∵7.5÷2.5=3(h),∴3小时后这人距离B送奶站最近.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
18.2 勾股定理的逆定理同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
(1)勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
说明:
①勾股定理的逆定理验证利用了三角形的全等.
②勾股定理的逆定理将数转化为形,作用是判断一个三角形是不是直角三角形.必须满足较小两边平方的和等于最大边的平方才能做出判断.
(2)运用勾股定理的逆定理解决问题的实质就是判断一个角是不是直角.然后进一步结合其他已知条件来解决问题.
注意:要判断一个角是不是直角,先要构造出三角形,然后知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
基础知识和能力拓展精练
一、选择题
1.以下列各组数为边长,能构成直角三角形的是( )
A. 4,5,6 B. 1,1, C. 6,8,11 D. 5,12,23
2.已知a,b,c是三角形的三边长,如果满足(a-6)2++=0,那么下列说法中不正确的是( )
A. 这个三角形是直角三角形 B. 这个三角形的最长边长是10
C. 这个三角形的面积是48 D. 这个三角形的最长边上的高是4.8
3.若a,b,C是△ABC的三条边,且满足a2﹣2ab+b2=0,(a+b)2=2ab+c2, 则△ABC的形状为( )
A. 直角三角形 B. 等腰三角形 C. 等边三角形 D. 等腰直角三角形
4.在平面直角坐标系中,点A(0,-1),点B(4,2),点C在坐标轴上,使∠ACB为直角的点C有( )个
A. 1 B. 2 C. 3 D. 4
5.如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A、B、C恰好在网格图中的格点上,那么△ABC中BC边上的高是( )
A. B. C. D.
6.如图,在由单位正方形组成的网格图标中有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的线段是( )
A. AB,CD,EF B. AB,CD,GH C. AB,EF,GH D. CD,EF,GH
7.小华和小刚兄弟两个同时从家去同一所学校上学,速度都是每分钟走50米.小华从家到学校走直线用了10分钟,而小刚从家出发先去找小明再到学校(均走直线),小刚到小明家用了6分钟,小明家到学校用了8分钟,小刚上学走了个( )
A. 锐角弯 B. 钝角弯 C. 直角弯 D. 不能确定
8.甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B,若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
A. 北偏西30° B. 南偏西30° C. 南偏东60° D. 南偏西60°
二、填空题
9.如图,平行四边形ABCD中,AC=4cm,BC=5cm,CD=3cm,则 ABCD的面积________.
10.把一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,则这个三角形是_______三角形.
11.如图所示的一块地, , , , , ,求这块地的面积__________.
12.如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5,则A,B,C,D四个小正方形的面积之和等于________ .
13.如图所示,AB⊥BC, ,CD=5,AD=3,BC=2,则∠A=_______度.
14.如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE= 4,AF=CE=3,则EF等于____.
三、解答题
15.已知:在△ABC中,∠A、∠B、∠C的对边分别是a、b、c,满足a2+b2+c2+338=10a+24b+26c.试判断△ABC的形状.
16.如图,已知正方形ABCD的边长为4,E为AB中点,F为AD上的一点,且AF=AD,试判断△EFC的形状.
17.龙梅和玉荣是草原上的好朋友,可是有一次经过一场争吵之后,两人不欢而散,龙梅的速度是米/秒,4分钟后她停了下来,觉得有点后悔了,玉荣走的方向好像是和龙梅成直角,她的速度是米/秒,如果她和龙梅同时停下来,而这时候她俩正好相距200米,那么她走的方向是否成直角?如果她们现在想讲和,那么原来的速度相向而行,多长时间后能相遇?
18.如图所示,在四边形ABCD中,AB=2,BC=2,CD=1,AD=5,且∠C=90°,求四边形ABCD的面积.
19.如图,甲、乙两船从港口A同时出发,甲船以30海里/时的速度向北偏东35°的方向航行,乙船以40海里/时的速度向另一方向航行,2小时后,甲船到达C岛,乙船到达B岛,若C,B两岛相距100海里,则乙船航行的方向是南偏东多少度?
20.已知:如图,AB=4,BC=12,CD=13,DA=3,AB⊥AD.
求证:BC⊥BD.
21.如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?
参考答案
1.B
【解析】选项B, ,满足勾股定理逆定理,A,C,D,不满足,故选B.
2.C
【解析】试题解析:∵(a-6)2≥0, +≥0,|c-10|≥0,(a-b)2++|c-10|=0,
∴a-6=0,b-8=0,c-10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴这个三角形是直角三角形,最长边为10,
∵6×8÷2=24,
∴这个三角形面积为24,
∵24×2÷10=4.8.
∴这个三角形最长边上的高为4.8.
故选C.
3.D
【解析】试题解析:
∴a b=0,即a=b,
∴△ABC为等腰三角形;
又
∴△ABC也是直角三角形;
∴△ABC为等腰直角三角形.
故选D.
点睛:如果一个三角形两边的平方和等于第三条边的平方,那么这个三角形是直角三角形.
4.C
【解析】试题解析:当C在x轴上时,有∠ACB=90°,此时C(4,0);
当C在y轴上时,设C(0,y),假设∠ACB=90°,则有:AC2+BC2=AB2.
∴1+y2+42+(2-y)2=52+22
整理得:y2-2y-4=0
解得: ,
∴点C的坐标为:(0, ),(0, )
故点C有三个.
故选C.
5.A
【解析】先用勾股定理耱出三角形的三边,再根据勾股定理的逆定理判断出△ABC是直角三角形,最后设BC边上的高为h,利用三角形面积公式建立方程即可得出答案.
解:由勾股定理得:
, , ,
,即
∴△ABC是直角三角形,
设BC边上的高为h,
则,
∴.
故选A.
点睛:本题主要考查勾股理及其逆定理.借助网格利用勾股定理求边长,并用勾股定理的逆定理来判断三角形是否是直角三角形是解题的关键.
6.C
【解析】由勾股定理知,EF=,AB=,CD=, ,
5+8=13, ,所以由勾股定理逆定理AB,EF,GH可以构成直角三角形.
所以选C.
点睛:
勾股定理:在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方.这个定理叫毕达哥拉斯定理,最早由毕达哥拉斯证明,中国商代发现了勾三股四弦五,仅仅是一个特例,严格讲不能叫定理.
设直角三角形两直角边为a和b,斜边为c,有 a2 + b2 = c2 .
勾股定理逆定理:如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.最长边所对的角为直角.
设三角形三边有 a2 + b2 = c2 . 则∠C=90°.
7.C
【解析】试题解析:∵小华从家到学校走直线用了10分钟,速度是每分钟走50米,
∴小华家到学校的直线距离=50×10=500(米);
∵小刚到小明家用了6分钟,
∴小刚到小明家的距离=50×6=300(米);
∵小明家到学校用了8分钟,
∴小明家到学校的距离=50×8=400(米).
∵3002+4002=5002,
∴小刚上学走了个直角弯.
故选C.
8.C
【解析】如图,根据题意得OA=40×15=600,OB=40×20=800,
因为6002=360000,8002=640000,10002=1000000,360000+640000=1000000.
所以6002+8002=10002.
所以∠AOB=∠AOB=90°,所以∠BOS=∠B′ON=60°,所以乙客轮的航行方向可能是南偏东60°或北偏西60°.
故选C.
9.12cm2
【解析】 ∵四边形ABCD是平行四边形,
∴AB=CD=3cm,
∵AC=4cm,BC=5cm,
∴AC2+AB2=AC2,
∴△ABC是直角三角形,
∴S△ABC=×3×4=6cm2,
∴则ABCD的面积=2×6=12cm2.
10.直角
【解析】试题解析:设中间长的边长为x,较长边为x+1,较短边为x-7,
∵此三角形周长为30米,
∴x+x+1+x-7=30,
解得:x=12,
则x+1=13,x-7=5,
∵52+122=132,
∴这个三角形的形状为直角三角形.
故答案为:直角.
11.
【解析】连接,
∵, , .
∴
.
∵.
∴.
∴.
∴
.
12.50
【解析】试题解析:∵所有的三角形都是直角三角形,
∴正方形A和C的面积和就是大正方形的面积,
同理,正方形B和D的面积和等于大正方形的面积,
∴四个小正方形的面积=2×5×5=50.
故答案为:50.
13.60
【解析】解:连接AC,∵AB⊥BC,∴AC===4,∴∠BAC=30°.
∵==25= ,∴∠DAC=90°,∴∠DAB=90°-30°=60°.故答案为:60.
14.
【解析】由题意得: 都是直角三角形.
,
15.见解析
【解析】试题分析:移项,配成三个完全平方;三个非负数的和为0,则都为0;已知a、b、c,利用勾股定理的逆定理判断三角形的形状为直角三角形.
试题解析:解:由已知可得a2-10a+25+b2-24b+144+c2-26c+169=0,
配方并化简得,(a-5)2+(b-12)2+(c-13)2=0.
∵(a-5)2≥0,(b-12)2≥0,(c-13)2≥0.
∴a-5=0,b-12=0,c-13=0.
解得a=5,b=12,c=13.
又∵a2+b2=169=c2,
∴△ABC是直角三角形.
16.见解析
【解析】试题分析:分别计算EF、CE、CF的长度,再利用勾股定理的逆定理判断即可.
试题解析:解:∵E为AB中点,∴BE=2.
∴CE2=BE2+BC2=22+42=20.
同理可求得,EF2=AE2+AF2=22+12=5,CF2=DF2+CD2=32+42=25.
∵CE2+EF2=CF2,
∴△EFC是以∠CEF为直角的直角三角形.
点睛:(1)勾股定理
直角三角形的两条直角边的平方和等于斜边的平方.这就是勾股定理.
(2)勾股定理逆定理
在一个三角形中,两条边的平方和等于另一条边的平方,那么这个三角形就是直角三角形. 这就是勾股定理的逆定理.
17.她们走的方向成直角,如果她们想讲和,按原来的速度相向而行,171秒后能相遇.
【解析】试题分析:首先分别计算出龙梅和玉荣走的路程,进而计算得出她们走的路程长度、她们之间的距离满足勾股定理,所以她们走的方向成直角,要计算她们相遇的时间,用总路程除以她们的速度和即可.
试题解析:
龙梅走的路程: ×4×60=120(米),
玉荣走的路程: ×4×60=160(米),
∵1202+1602=2002,
∴她们走的方向成直角,
以原来的速度相向而行相遇的时间:200÷(+)=200÷ = =171(秒);
答:她们走的方向成直角,如果她们想讲和,按原来的速度相向而行,171秒后能相遇.
点睛:本题关键在于勾股定理逆定理的运用.
18.四边形ABCD的面积是6.
【解析】试题分析:连接BD,根据勾股定理可计算出BD的长度,再由勾股定理逆定理可判断出△ABD为直角三角形,分别计算出△ABD和△BCD的面积,求和即可.
试题解析:
连接BD,
∵∠C=90°,
∴△BCD为直角三角形,
∴BD2=BC2+CD2=22+12=()2,BD>0,
∴BD=,
在△ABD中,
∵AB2+BD2=20+5=25,AD2=52=25,
∴AB2+BD2=AD2,
∴△ABD为直角三角形,且∠ABD=90°,
∴S四边形ABCD=S△ABD+S△BCD=×2×+×2×1=6.
∴四边形ABCD的面积是6.
点睛:本题关键在于利用勾股定理逆定理判定出直角三角形,从而求出三角形的面积.
19.乙船航行的方向为南偏东55°.
【解析】试题分析:
由题意可知:在△ABC中,AC=60,AB=80,BC=100,由此可由“勾股定理逆定理”证得∠BAC=90°,结合∠EAD=180°和∠EAC=35°即可求得∠DAB的度数,从而得到乙船的航行方向.
试题解析:
由题意可知,在△ABC中,AC=30×2=60,AB=40×2=80,BC=100,
∴AC2=3600,AB2=6400,BC2=10000,
∴AC2+AB2=BC2,
∴∠CAB=90°,
又∵∠EAD=180°,∠EAC=35°,
∴∠DAB=90°-∠CAE=90°-35°=55°,
∴乙船航行的方向为南偏东55°.
点睛:本题的解题要点是:在△ABC中,由已知条件先求得AC和AB的长,再结合AC=100,即可用“勾股定理的逆定理”证得∠BAC=90°,这样即可求出∠DAB的度数,从而使问题得到解决.
20.见解析
【解析】试题分析:欲求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
试题解析: ,
在中, ,
在中,
,
.
21.3h.
【解析】试题分析:首先根据勾股定理逆定可证明△ABC是直角三角形,然后计算出∠BCD的度数,再根据直角三角形的性质算出DC的长,然后根据速度和路程可计算出多长时间后这人距离B送奶站最近.
试题解析:解:过B作BD⊥公路于D.∵82+152=172,∴AC2+BC2=AB2,∴△ABC是直角三角形,且∠ACB=90°.
∵∠1=30°,∴∠BCD=180°-90°-30°=60°.
在Rt△BCD中,∵∠BCD=60°,∴∠CBD=30°,∴CD=BC=×15=7.5(km).
∵7.5÷2.5=3(h),∴3小时后这人距离B送奶站最近.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
